声明:本文原创,转载请注明出处
前言
本文写的超级详细,仔细阅读一定会读懂~有疑问的同学欢迎留言!
我们都知道,splay tree可达到分摊O(logn)的时间复杂度,但这个复杂度是怎么得到的呢?下面我们通过引入势能的概念加以分析。
势能
节点v的势能定义为:以节点v为根的子树的大小取对数,即 ϕ \phi ϕ(v) = log(size(v)),本文里面的log默认以2为底。整棵树的势能是每个节点的势能之和 ϕ \phi ϕ= ∑ v ϕ ( v ) \sum_{v}\phi(v) ∑vϕ(v)
直观上来讲,一棵树越“倾斜”,势能越高;反之,一棵树越“平衡”,势能就越低。下面证明,最倾斜的情况下(树退化为链表),势能为O(logn);最平衡的情况下(满树),势能为为O(n)。
-
链表情况: ∑ v l o g ( s i z e ( v ) ) \sum_{v}log(size(v)) ∑vlog(size(v)) = ∑ k = 1 n l o g ( k ) \sum_{k=1}^{n}log(k) ∑k=1nlog(k) = l o g ∏ k = 1 n k log\prod_{k=1}^nk log∏k=1nk = l o g n ! logn! logn! = O ( n l o g n ) O(nlogn) O(nlogn)
-
满树情况:设树的高度为h,节点v的深度为d,则size(v) = 2 d + 1 − 1 2^{d+1}-1 2d+1−1,和v深度相同的节点共有 2 h − d 2^{h-d} 2h−d个。 ∑ v l o g ( s i z e ( v ) ) = ∑ d = 0 h 2 h − d l o g ( 2 d + 1 − 1 ) < ∑ d = 0 h 2 h − d l o g 2 d + 1 = ∑ d = 0 h 2 h − d ( d + 1 ) = 2 h + 2 − h − 3 = O ( n ) \sum_{v}log(size(v))=\sum_{d=0}^h2^{h-d}log(2^{d+1}-1)<\sum_{d=0}^h2^{h-d}log2^{d+1}=\sum_{d=0}^h2^{h-d}(d+1)=2^{h+2}-h-3=O(n) ∑vlog(size(v))=∑d=0h2h−dlog(2d+1−1)<∑d=0h2h−dlog2d+1=∑d=0h2h−d(d+1)=2h+2−h−3=O(n)
核心公式 A ( k ) A_{(k)} A(k) = T ( k ) T_{(k)} T(k) + Δ ϕ ( k ) \Delta\phi_{(k)} Δϕ(k)
假设我们一共有m次操作,我们的目的是证明这m次操作花费的总时间T=O(mlogn)。我们接下来的分析围绕着一个公式:
A
(
k
)
A_{(k)}
A(k) =
T
(
k
)
T_{(k)}
T(k) +
Δ
ϕ
(
k
)
\Delta\phi_{(k)}
Δϕ(k),k=1,2…m。其中k表示的是第k次操作。把这k个公式累加,
A
=
∑
k
=
1
m
A
k
A=\sum_{k=1}^mA_k
A=∑k=1mAk,
T
=
∑
k
=
1
m
T
k
T=\sum_{k=1}^mT_k
T=∑k=1mTk,得到公式:
A
=
T
+
ϕ
m
−
ϕ
0
A=T+\phi_m-\phi_0
A=T+ϕm−ϕ0.
下面我解释一下A,T,
ϕ
\phi
ϕ的含义:
- T:花费的时间;
- ϕ \phi ϕ:整棵树的势能;
- A:“代价”(又称摊还代价)
所以 A ( k ) A_{(k)} A(k) = T ( k ) T_{(k)} T(k) + Δ ϕ ( k ) \Delta\phi_{(k)} Δϕ(k)这个公式的含义就是:每次操作的“代价”就是这次操作所花费的时间和势能增量之和。
我们已经知道, ϕ m − ϕ 0 = O ( n l o g n ) \phi_m-\phi_0=O(nlogn) ϕm−ϕ0=O(nlogn),代入 A = T + ϕ m − ϕ 0 A=T+\phi_m-\phi_0 A=T+ϕm−ϕ0得到: A = T + O ( n l o g n ) A=T+O(nlogn) A=T+O(nlogn)。现在我们的证明已经完成了一半。我们想要证明T=O(mlogn),接下来只需证明A=O(mlogn)。实际上,我们可以证明 A ( k ) = O ( l o g n ) A_{(k)}=O(logn) A(k)=O(logn),然后对m个 A ( k ) A_{(k)} A(k)求和即可。
证明 A ( k ) = O ( l o g n ) A_{(k)}=O(logn) A(k)=O(logn)
求子步骤代价 A ( k ) i A_{(k)}^i A(k)i
为了描述方便,设 r a n k ( v ) = l o g ( s i z e ( v ) ) rank(v)=log(size(v)) rank(v)=log(size(v))
假设我们要对节点v做splay操作,即把v从原位置伸展至根。整个splay操作可以被分割成多个子操作:除了最后一个子操作外,每个子操作把v提升两层,最后一个子操作有可能把v提升一层或者两层(与v的深度的奇偶有关)。每个子操作不外乎属于以下几种之一:zig,zag,zig-zig,zag-zag,zig-zag,zag-zig。下面我们分情况讨论:
-
zig/zag
我们详细说明zig,zag的情况和zig是对称的。
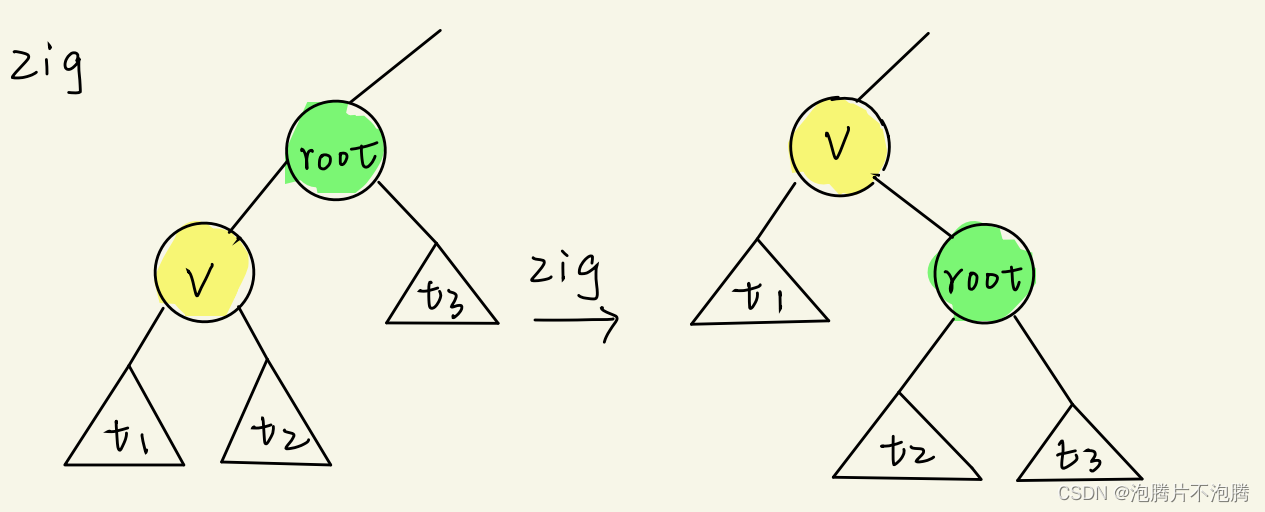
A ( k ) i = T ( k ) i + Δ ϕ ( k ) i A_{(k)}^i=T_{(k)}^i+\Delta\phi_{(k)}^i A(k)i=T(k)i+Δϕ(k)i (1)在子操作i中,整棵树里只有v和root两个节点的势能可能变化。故有:
A ( k ) i = T ( k ) i + Δ r a n k ( k ) i ( v ) + Δ r a n k ( k ) i ( r o o t ) A_{(k)}^i=T_{(k)}^i+\Delta rank_{(k)}^i(v)+\Delta rank_{(k)}^i(root) A(k)i=T(k)i+Δrank(k)i(v)+Δrank(k)i(root) (2)
而root子树的size减小了,因此 Δ ϕ ( k ) i ( r o o t ) < 0 \Delta\phi_{(k)}^i(root)<0 Δϕ(k)i(root)<0,故:
A ( k ) i < T ( k ) i + Δ r a n k ( k ) i ( v ) A_{(k)}^i<T_{(k)}^i+\Delta rank_{(k)}^i(v) A(k)i<T(k)i+Δrank(k)i(v) (3)
因为被提升点v只上升了一层,故 T ( k ) i = 1 T_{(k)}^i=1 T(k)i=1:
A ( k ) i < 1 + Δ r a n k ( k ) i ( v ) A_{(k)}^i<1+\Delta rank_{(k)}^i(v) A(k)i<1+Δrank(k)i(v) (4)
-
zig-zag/zag-zig
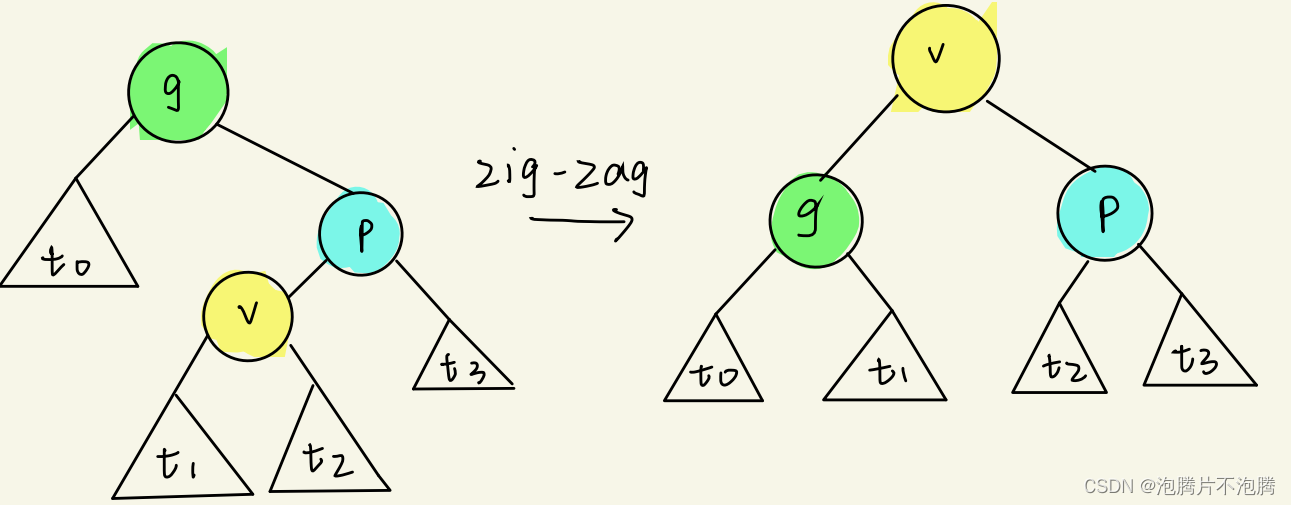
A ( k ) i = T ( k ) i + Δ ϕ ( k ) i A_{(k)}^i=T_{(k)}^i+\Delta\phi_{(k)}^i A(k)i=T(k)i+Δϕ(k)i (1)在子操作i中,整棵树里只有v,p,g三个节点的势能可能变化。故有:
A ( k ) i = T ( k ) i + Δ r a n k ( k ) i ( v ) + Δ r a n k ( k ) i ( p ) + Δ r a n k ( k ) i ( g ) A_{(k)}^i=T_{(k)}^i+\Delta rank_{(k)}^i(v)+\Delta rank_{(k)}^i(p)+\Delta rank_{(k)}^i(g) A(k)i=T(k)i+Δrank(k)i(v)+Δrank(k)i(p)+Δrank(k)i(g) (2)
A ( k ) i = T ( k ) i + r a n k ( k ) i ( v ) − r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( p ) − r a n k ( k ) i − 1 ( p ) + r a n k ( k ) i ( g ) − r a n k ( k ) i − 1 ( g ) A_{(k)}^i=T_{(k)}^i+rank_{(k)}^i(v)-rank_{(k)}^{i-1}(v)+rank_{(k)}^i(p)- rank_{(k)}^{i-1}(p)+rank_{(k)}^{i}(g)-rank_{(k)}^{i-1}(g) A(k)i=T(k)i+rank(k)i(v)−rank(k)i−1(v)+rank(k)i(p)−rank(k)i−1(p)+rank(k)i(g)−rank(k)i−1(g) (3)
容易看出 r a n k ( k ) i ( v ) = r a n k ( k ) i − 1 ( g ) rank_{(k)}^i(v)=rank_{(k)}^{i-1}(g) rank(k)i(v)=rank(k)i−1(g),上式化简为:
A ( k ) i = 2 − r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( p ) − r a n k ( k ) i − 1 ( p ) + r a n k ( k ) i ( g ) A_{(k)}^i=2-rank_{(k)}^{i-1}(v)+rank_{(k)}^i(p)-rank_{(k)}^{i-1} (p)+rank_{(k)}^{i}(g) A(k)i=2−rank(k)i−1(v)+rank(k)i(p)−rank(k)i−1(p)+rank(k)i(g) (4)
因为 r a n k ( k ) i − 1 ( p ) > r a n k ( k ) i − 1 ( v ) rank_{(k)}^{i-1}(p)>rank_{(k)}^{i-1}(v) rank(k)i−1(p)>rank(k)i−1(v):
A ( k ) i < 2 − 2 r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( p ) + r a n k ( k ) i ( g ) A_{(k)}^i<2-2rank_{(k)}^{i-1}(v)+rank_{(k)}^i(p)+rank_{(k)}^{i}(g) A(k)i<2−2rank(k)i−1(v)+rank(k)i(p)+rank(k)i(g) (5)
因为: r a n k ( k ) i ( p ) + r a n k ( k ) i ( g ) = l o g ( s i z e ( p i ) ) + l o g ( s i z e ( g i ) ) < 2 l o g ( ( s i z e ( p i ) + s i z e ( g i ) ) / 2 ) = 2 l o g ( ( s i z e ( v i ) − 1 ) / 2 ) < 2 l o g ( s i z e ( v i ) ) − 2 = 2 r a n k ( k ) i ( v ) − 2 rank_{(k)}^i(p)+rank_{(k)}^{i}(g)=log(size(p_i))+log(size(g_i))<2log((size(p_i)+size(g_i))/2)=2log((size(v_i)-1)/2)<2log(size(v_i))-2=2rank_{(k)}^i(v)-2 rank(k)i(p)+rank(k)i(g)=log(size(pi))+log(size(gi))<2log((size(pi)+size(gi))/2)=2log((size(vi)−1)/2)<2log(size(vi))−2=2rank(k)i(v)−2
A ( k ) i < 2 r a n k ( k ) i ( v ) − 2 r a n k ( k ) i − 1 ( v ) A_{(k)}^i<2rank_{(k)}^i(v)-2rank_{(k)}^{i-1}(v) A(k)i<2rank(k)i(v)−2rank(k)i−1(v) (6)
-
zig-zig/zag-zag
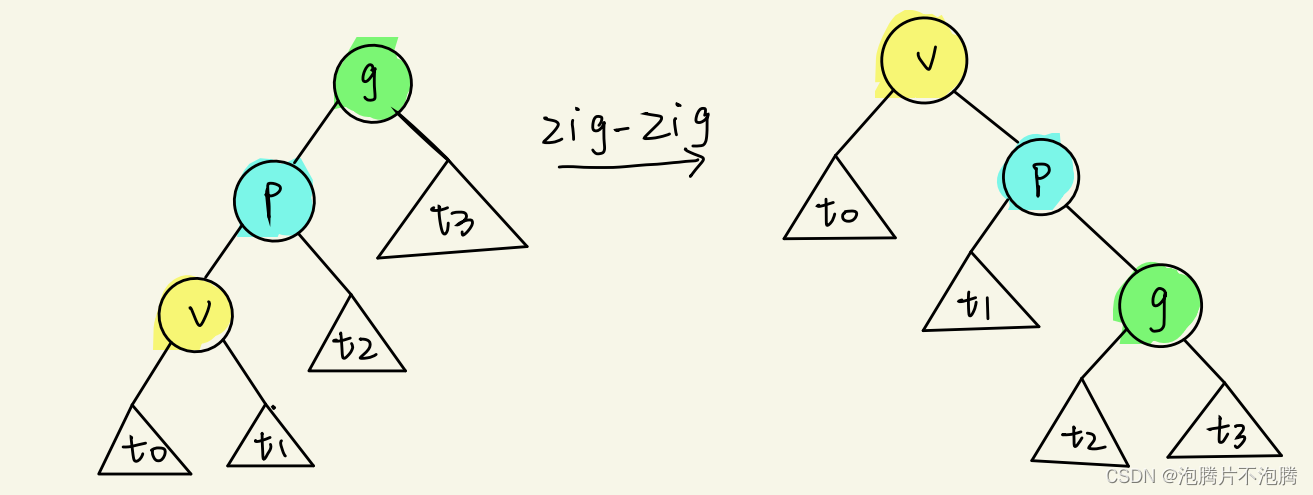
A ( k ) i = T ( k ) i + Δ ϕ ( k ) i A_{(k)}^i=T_{(k)}^i+\Delta\phi_{(k)}^i A(k)i=T(k)i+Δϕ(k)i (1)在子操作i中,整棵树里只有v,p,g三个节点的势能可能变化。故有:
A ( k ) i = T ( k ) i + Δ r a n k ( k ) i ( v ) + Δ r a n k ( k ) i ( p ) + Δ r a n k ( k ) i ( g ) A_{(k)}^i=T_{(k)}^i+\Delta rank_{(k)}^i(v)+\Delta rank_{(k)}^i(p)+\Delta rank_{(k)}^i(g) A(k)i=T(k)i+Δrank(k)i(v)+Δrank(k)i(p)+Δrank(k)i(g) (2)
A ( k ) i = T ( k ) i + r a n k ( k ) i ( v ) − r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( p ) − r a n k ( k ) i − 1 ( p ) + r a n k ( k ) i ( g ) − r a n k ( k ) i − 1 ( g ) A_{(k)}^i=T_{(k)}^i+rank_{(k)}^i(v)-rank_{(k)}^{i-1}(v)+rank_{(k)}^i(p)-rank_{(k)}^{i-1}(p)+rank_{(k)}^{i}(g)-rank_{(k)}^{i-1}(g) A(k)i=T(k)i+rank(k)i(v)−rank(k)i−1(v)+rank(k)i(p)−rank(k)i−1(p)+rank(k)i(g)−rank(k)i−1(g) (3)
容易看出 r a n k ( k ) i ( v ) = r a n k ( k ) i − 1 ( g ) rank_{(k)}^i(v)=rank_{(k)}^{i-1}(g) rank(k)i(v)=rank(k)i−1(g),上式化简为:
A ( k ) i = 2 − r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( p ) − r a n k ( k ) i − 1 ( p ) + r a n k ( k ) i ( g ) A_{(k)}^i=2-rank_{(k)}^{i-1}(v)+rank_{(k)}^i(p)-rank_{(k)}^{i-1}(p)+rank_{(k)}^{i}(g) A(k)i=2−rank(k)i−1(v)+rank(k)i(p)−rank(k)i−1(p)+rank(k)i(g) (4)因为 r a n k ( k ) i − 1 ( p ) > r a n k ( k ) i − 1 ( v ) rank_{(k)}^{i-1}(p)>rank_{(k)}^{i-1}(v) rank(k)i−1(p)>rank(k)i−1(v):
A ( k ) i < 2 − 2 r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( p ) + r a n k ( k ) i ( g ) A_{(k)}^i<2-2rank_{(k)}^{i-1}(v)+rank_{(k)}^i(p)+rank_{(k)}^{i}(g) A(k)i<2−2rank(k)i−1(v)+rank(k)i(p)+rank(k)i(g) (5)到(5)为止,zig-zig的证明过程均与zig-zag相同。
A ( k ) i < 2 − 3 r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( p ) + r a n k ( k ) i ( g ) + r a n k ( k ) i − 1 ( v ) A_{(k)}^i<2-3rank_{(k)}^{i-1}(v)+rank_{(k)}^i(p)+rank_{(k)}^{i}(g)+rank_{(k)}^{i-1}(v) A(k)i<2−3rank(k)i−1(v)+rank(k)i(p)+rank(k)i(g)+rank(k)i−1(v) (6)因为 r a n k ( k ) i ( p ) < r a n k ( k ) i ( v ) rank_{(k)}^i(p)<rank_{(k)}^i(v) rank(k)i(p)<rank(k)i(v):
A ( k ) i < 2 − 3 r a n k ( k ) i − 1 ( v ) + r a n k ( k ) i ( v ) + r a n k ( k ) i ( g ) + r a n k ( k ) i − 1 ( v ) A_{(k)}^i<2-3rank_{(k)}^{i-1}(v)+rank_{(k)}^i(v)+rank_{(k)}^{i}(g)+rank_{(k)}^{i-1}(v) A(k)i<2−3rank(k)i−1(v)+rank(k)i(v)+rank(k)i(g)+rank(k)i−1(v) (7)因为 r a n k ( k ) i ( g ) + r a n k ( k ) i − 1 ( v ) = l o g ( s i z e ( t 2 + t 3 + 1 ) ) + l o g ( s i z e ( t 0 + t 1 + 1 ) ) < 2 l o g ( s i z e ( t 0 + t 1 + t 2 + t 3 + 2 ) / 2 ) < 2 l o g ( s i z e ( v i ) ) − 2 = 2 r a n k ( k ) i ( v ) − 2 rank_{(k)}^{i}(g)+rank_{(k)}^{i-1}(v)=log(size(t2+t3+1))+log(size(t0+t1+1))<2log(size(t0+t1+t2+t3+2)/2)<2log(size(v_i))-2=2rank_{(k)}^i(v)-2 rank(k)i(g)+rank(k)i−1(v)=log(size(t2+t3+1))+log(size(t0+t1+1))<2log(size(t0+t1+t2+t3+2)/2)<2log(size(vi))−2=2rank(k)i(v)−2:
A ( k ) i < 3 r a n k ( k ) i ( v ) − 3 r a n k ( k ) i − 1 A_{(k)}^i<3rank_{(k)}^i(v)-3rank_{(k)}^{i-1} A(k)i<3rank(k)i(v)−3rank(k)i−1 (8)
总结一下,到目前为止,我们已经得到了三种子步骤的代价公式:
- zig/zag: A ( k ) i < 1 + r a n k ( k ) i ( v ) − r a n k ( k ) i − 1 ( v ) A_{(k)}^i<1+ rank_{(k)}^i(v)-rank_{(k)}^{i-1}(v) A(k)i<1+rank(k)i(v)−rank(k)i−1(v) (1)
- zig-zag/zag-zig: A ( k ) i < 2 r a n k ( k ) i ( v ) − 2 r a n k ( k ) i − 1 ( v ) A_{(k)}^i<2rank_{(k)}^i(v)-2rank_{(k)}^{i-1}(v) A(k)i<2rank(k)i(v)−2rank(k)i−1(v) (2)
- zig-zig/zag-zag: A ( k ) i < 3 r a n k ( k ) i ( v ) − 3 r a n k ( k ) i − 1 A_{(k)}^i<3rank_{(k)}^i(v)-3rank_{(k)}^{i-1} A(k)i<3rank(k)i(v)−3rank(k)i−1 (3)
每个操作的代价 A ( k ) = ∑ i A ( k ) i A_{(k)}=\sum_iA_{(k)}^i A(k)=∑iA(k)i
我们已经得到了每个子步骤的“代价”,欲得到整个操作的代价,只需把这些子步骤的代价求和。
case 1
我们首先假设v在splay至根时,上升的层数是偶数层,也就是说,我们只用到了子步骤zig-zag/zag-zig/zig-zig/zag-zag(只使用了公式(2)和(3))。
对于(2),我们知道: 2 r a n k ( k ) i ( v ) − 2 r a n k ( k ) i − 1 ( v ) < 3 r a n k ( k ) i ( v ) − 3 r a n k ( k ) i − 1 ( v ) 2rank_{(k)}^i(v)-2rank_{(k)}^{i-1}(v)<3rank_{(k)}^i(v)-3rank_{(k)}^{i-1}(v) 2rank(k)i(v)−2rank(k)i−1(v)<3rank(k)i(v)−3rank(k)i−1(v)
因此,(2)和(3)都可以写为: A ( k ) i < 3 r a n k ( k ) i ( v ) − 3 r a n k ( k ) i − 1 A_{(k)}^i<3rank_{(k)}^i(v)-3rank_{(k)}^{i-1} A(k)i<3rank(k)i(v)−3rank(k)i−1
假设一共有x个子步骤,我们对这x个式子求和: A ( k ) = ∑ i = 1 x A ( k ) i < 3 r a n k ( k ) x ( v ) − 3 r a n k ( k ) 0 ( v ) < 3 r a n k ( k ) x ( v ) = O ( l o g n ) A_{(k)}=\sum_{i=1}^xA_{(k)}^i<3rank_{(k)}^x(v)-3rank_{(k)}^0(v)<3rank_{(k)}^x(v)=O(logn) A(k)=∑i=1xA(k)i<3rank(k)x(v)−3rank(k)0(v)<3rank(k)x(v)=O(logn)
case 2
v在splay至根时,上升的层数是奇数层。此时,我们用到了公式(1)(2)(3)。
同样地,我们可以把公式1放缩: A ( k ) i < 1 + r a n k ( k ) i ( v ) − r a n k ( k ) i − 1 ( v ) < 1 + 3 r a n k ( k ) i ( v ) − 3 r a n k ( k ) i − 1 A_{(k)}^i<1+ rank_{(k)}^i(v)-rank_{(k)}^{i-1}(v)<1+3rank_{(k)}^i(v)-3rank_{(k)}^{i-1} A(k)i<1+rank(k)i(v)−rank(k)i−1(v)<1+3rank(k)i(v)−3rank(k)i−1
现在我们把这x个式子求和,注意(1)只使用了一次:
A ( k ) = ∑ i = 1 x A ( k ) i < 1 + 3 r a n k ( k ) x ( v ) − 3 r a n k ( k ) 0 ( v ) < 3 r a n k ( k ) x ( v ) = O ( l o g n ) A_{(k)}=\sum_{i=1}^xA_{(k)}^i<1+3rank_{(k)}^x(v)-3rank_{(k)}^0(v)<3rank_{(k)}^x(v)=O(logn) A(k)=∑i=1xA(k)i<1+3rank(k)x(v)−3rank(k)0(v)<3rank(k)x(v)=O(logn)
总结
全文围绕公式 A = T + Δ ϕ A=T+\Delta\phi A=T+Δϕ
我们先证明了 ϕ = O ( n l o g n ) \phi=O(nlogn) ϕ=O(nlogn),故 Δ ϕ = O ( n l o g n ) \Delta\phi=O(nlogn) Δϕ=O(nlogn);
我们证明了每个操作的代价 A ( k ) = O ( l o g n ) A_{(k)}=O(logn) A(k)=O(logn),对m个操作求和,总代价为 A = O ( m l o g n ) A=O(mlogn) A=O(mlogn);
对于m>>n的情况, T = A − Δ ϕ = O ( m l o g n ) T=A-\Delta\phi=O(mlogn) T=A−Δϕ=O(mlogn),每次操作的均摊时间复杂度为O(logn)





















 934
934

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








