前言:
目前我们现实生活中使用的graph都是大规模的graph,节点数量可以很轻松的达到亿级甚至十亿级别,边数量就更多了,在实际生活中具有价值的graph大多数的节点数量都在这些范围中,所以我们必须用一些方法来使我们的GNNS拓展到这些大型的graph中去。
一:为什么说拓展到大型graph中很难?
(1):首先如下图给出:

我们知道我们更新我们的模型是通过最小化我们loss来进行的。
在loss-function中我们最常用到的就是随机梯度下降(SGD)来最小化loss,标准的SGD工作如下:
首先在N个总节点随机采样M个节点(也称为mini-batches),然后通过M个节点更新平均loss来代替整个计算过程。
(2):如果我们使用了标准SGD的方法来计算loss,我们会发现,如果我们在用采样的方法随机选取N个节点时,在graph表示很多节点都是很孤立的如下图(因为我们知道graph中的节点是由边来连接的)这样的话GNN中就没达到他们的邻居节点,也就是说embeddings不会很好,所以说标准的SGD方法对GNNS的更新来说是比较乏力的。
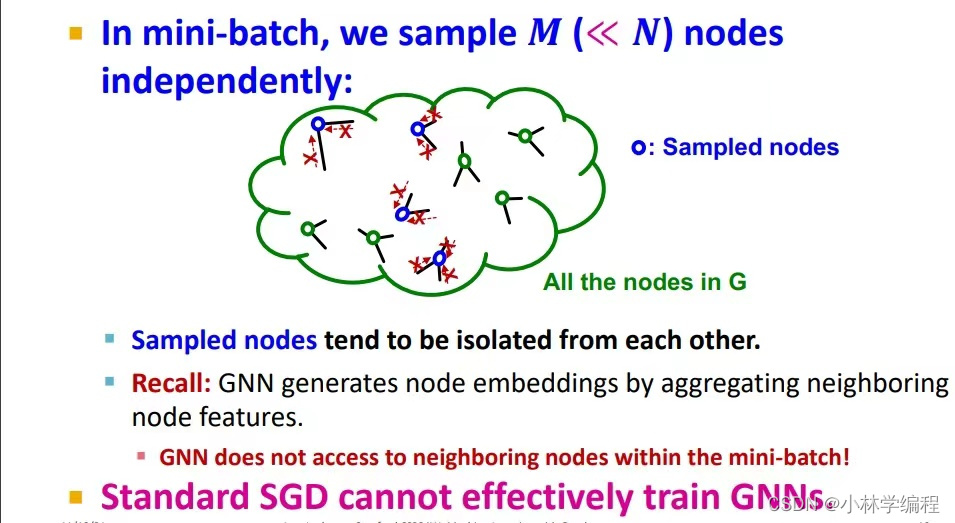
(3):如果我们不随机采样,而进行全图采样(full-batch)的话,虽然这样训练的loss是最真实和准确的,但是如下图所示这样的话就没办法把数据全部加载到计算速度更快的GPU当中(内存问题),如果说在CPU上计算又会十分的缓慢。

二:三种解决方法:
已经从上文知道了我们拓展的难度接下来我们将介绍三种拓展方法:
(1):Neighbor Sampling
(2):Cluster-GCN
(3):Simplified GCN
ps:本文中会讲到(1)方法,其他两种方法在这个系列之后讲。
三:Neighbor Sampling:
回顾:
GNNS通常的node embeddings是以下图右边这种形式展开的。(当我们选择embedding‘0’这一个节点时,如果是1个hop就只要吸收节点1,2,3(邻居节点)的node feature,以此类推,所以有了下图右图中的计算图)。
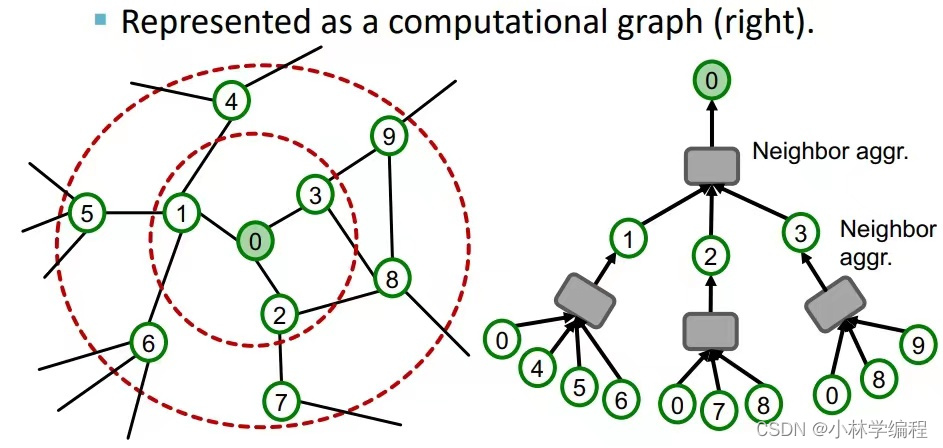
以上我们可以得出一个结论:就是如果我们需要embedding一个节点,我们只需要知道它周围k-hops的节点作为它的计算图(不需要知道全部graph中节点),所以在一个mini-batch中的M个需要embeddings时,我们可以举出M个k-hops的计算图(每个计算图可以存储在GPU中):
所以,这样我们就可以使用SGD来进行参数更新步骤如下:
随机选择M个节点(在总节点数为N且远远大于M)---对于每一样本节点v先获得它k-hops的计算图---计算节点v的embedding---计算参数的loss---用SGD进行减小loss。(可在GPU上完成运算)
这样来看似乎很完美,但实际上还存在着问题:如下图左图所示,如果要存在k-hops都要加载进GPU时,节点数量随着hops的上升还是以指数形式的还是很多的;如下图右图所示,有可能存在‘Hub node’(可以认为是high degree节点,简单来说就是这个节点他的邻居节点非常多),这样也会使节点数量严重超标,进而GPU存储不下。如何解决呢?
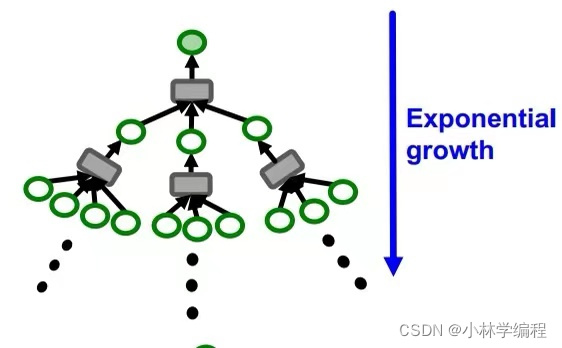
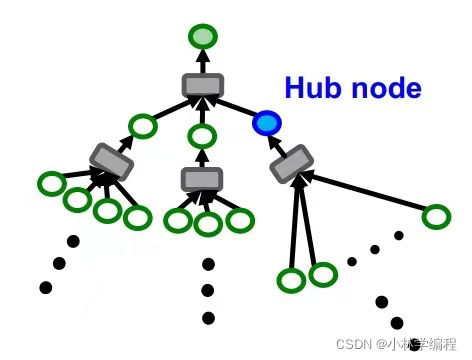
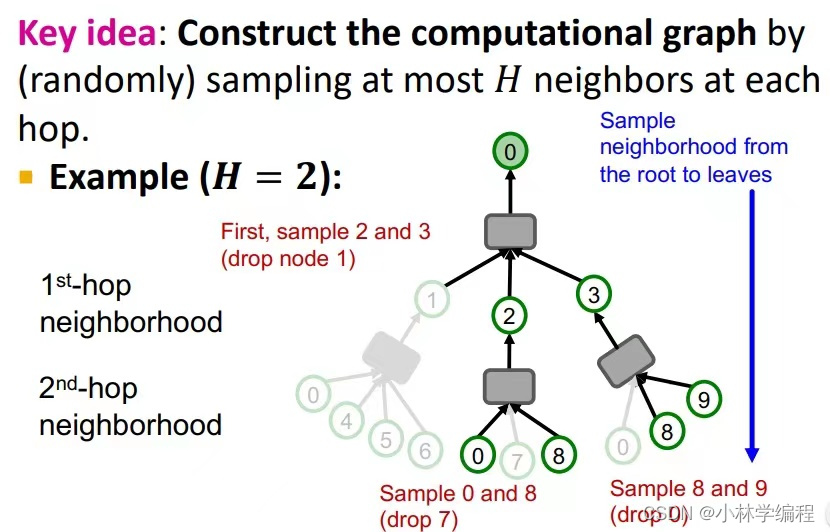
我们解决这个问题的方法有点相似于‘dropout’,就是说我们需要设定一个参数H(假设H=2,则在每一级节点都只选择两个邻居,如下图),这样做大大减少了节点数量,容易送到GPU中训练。
四:Neighbor Sampling的注意事项
以上,我们差不多可以将GNNS拓展到大规模graph了,但是运用这种方法也需要注意以下几点:
(1):权衡好取样数量参数H:
更小的H,邻居聚合embeddings的效率就越高,但是作为代价就是训练结果不稳定,embeddings的准确度不高,所以在实际运用中需要权衡好两者的关系。
(2):运算时间:
即使使用了‘Neighbor Sampling’,计算图的规模仍然很大,所以在选择多少hops时,也需要谨慎选择,因为越到后面,每增加一个hop,计算的花费也就越大。
(3):怎样采样节点:
上文中我们仅仅是用到‘random sampling’(随机取样),这样虽然很快,但是可能会随机到一些不是那么重要的节点,会导致embedding的准确度下降。
所以我们可以选择‘random walk with restarts’(重启随机游走算法)(主要作用就是重启随机游走可以捕捉两个节点之间多方面的关系,捕捉图的整体结构信息,从而能选择更重要的邻居节点,具体的算法看最下的链接文章中有详细介绍)如下图:

五:参考链接:
1:cs224w的17.1,17.2
【斯坦福 CS224W】图机器学习( 中英字幕 | 2021秋) Machine Learning with Graphs by Jure Leskovec_哔哩哔哩_bilibili
2:重启随机游走算法:







 本文探讨了在处理大规模图数据时,图神经网络(GNNs)面临的挑战以及解决方案。首先解释了全图采样导致的内存问题和随机采样可能导致的孤立节点问题。接着介绍了NeighborSampling方法,该方法通过限制每个节点的邻居采样数量,有效地减少计算图规模,使其适应GPU计算。然而,这种方法也存在节点数量随跳数指数增长和高度连接节点(Hubnodes)的问题。为了解决这些问题,提出了类似于dropout的策略,即在每个层级只采样一定数量的邻居。最后,指出了在应用NeighborSampling时需要注意的事项,包括采样数量的权衡、运算时间和节点采样策略的选择。
本文探讨了在处理大规模图数据时,图神经网络(GNNs)面临的挑战以及解决方案。首先解释了全图采样导致的内存问题和随机采样可能导致的孤立节点问题。接着介绍了NeighborSampling方法,该方法通过限制每个节点的邻居采样数量,有效地减少计算图规模,使其适应GPU计算。然而,这种方法也存在节点数量随跳数指数增长和高度连接节点(Hubnodes)的问题。为了解决这些问题,提出了类似于dropout的策略,即在每个层级只采样一定数量的邻居。最后,指出了在应用NeighborSampling时需要注意的事项,包括采样数量的权衡、运算时间和节点采样策略的选择。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










