最小二乘法的状态转移方程（3）

最新推荐文章于 2024-06-15 11:44:36 发布

矢志航天的阿洪

最新推荐文章于 2024-06-15 11:44:36 发布

阅读量373

点赞数 4

文章标签：最小二乘法算法机器学习

本文链接：https://blog.csdn.net/weixin_57997461/article/details/137464217

版权

一、地球球形摄动理论

在关于未受扰动的开普勒运动的导言一章中，假设地球的总质量集中在坐标系的中心和引力

$\ddot{\boldsymbol{r}}=-\frac{GM_{\bigoplus }}{r^3}\boldsymbol{r}$

因此，可以用来计算卫星在 $\boldsymbol{r}$ 处所感受到的加速度。为了讨论一个更现实的模型，方便地使用涉及相应重力势梯度的等价表示。

$\ddot{\boldsymbol{r}}=\bigtriangledown U,U=GM_{\bigoplus}\frac{1}{r}$

通过总结单个质量元素的贡献，这个势的表达式可以很容易地推广到任意的质量分布，取一体积微元，其表达式为 $\textup{d}m=\rho(\boldsymbol{s})\textup{d}^{3}\boldsymbol{s}$ ，则得到每一体积微元的势函数表达式可以写为

$U=G\int \frac{\rho(\boldsymbol{s})\textup{d}^{3}\boldsymbol{s}}{\left | \boldsymbol{r}-\boldsymbol{s} \right |}$

这里 $\rho(\boldsymbol{s})$ 表示地球内部某个点的密度， $\left | \boldsymbol{r}-\boldsymbol{s} \right |$ 是卫星到这个地方的距离

球形谐波的展开

为了求出上述方程的积分，将距离的导数可以展开为一系列的勒让德多项式。对于 $r>s$ ，它适用于边界球体外的所有点 $\boldsymbol{r}$ ，我们有

$\frac{1}{\left | \boldsymbol{r}-\boldsymbol{s} \right |}=\frac{1}{r}\sum_{n=0}^{\infty }(\frac{s}{r})^nP_n(\cos{(\gamma)})\\\cos{\gamma}=\frac{\boldsymbol{r}\cdot \boldsymbol{s}}{rs}$

在这里 $P_n(u)=\frac{1}{2^nn!}\frac{\textup{d}^n}{\boldsymbol{d}u^n}(u^2-1)^n$ 是n次幂勒让德多项式， $\gamma$ 角是 $\boldsymbol{r},\boldsymbol{s}$ 之间的夹角。引入经度 $\lambda$ （正向东计算）和纬度 $\phi$ ，位置信息被描述为

$x=r\cos\phi \cos\lambda\\ y=r\cos\phi \sin\lambda\\ z=r\sin\phi$

同样，对于s对应的 $\lambda ',\phi '$ ，我们可以用勒让德多项式的加法定理

在这里 $P_{nm}$ ，它被称为n次m阶的缔合勒让德多项式，被定义为

$P_{nm}(u)=(1-u^2)^{m/2}\frac{\textup{d}^m}{\boldsymbol{d}u^m}P_n(u)$

现在人们可以用这样的形式写出地球重力势

$U=\frac{GM_e}{r}[1+\sum_{n=2}^{\infty}\sum_{m=0}^{n}(\frac{a_e}{r})^nP_{n,m}(\sin \varphi)(C_{n,m}\cos(m\lambda)+S_{n,m}\sin(m\lambda))]$

式中： $G$ 为万有引力常数； $M_e$ 为地球质量； $a_e$ 为地球赤道平均半径； $r,\lambda,\varphi$ 为地心地球固连坐标系中的球坐标。 $C_{n,m},S_{n,m}$ 是级数的n阶m次系数，称为球谐系数。

这里计算勒让德多项式，需要应用递归的方式，由勒让德多项式的性质

$P_{mm}(u)=(2m-1)(1-u^2)^{1/2}P_{m-1,m-1}\\P_{m+1,m}(u)=(2m+1)uP_{mm}(u)\\ P_{nm}(u)=\frac{1}{n-m}((2n-1)uP_{n-1,m}(u)-(n+m-1)P_{n-2,m}(u))$

同时根据三角函数公式得到

对于角的经度函数变成一个递归。这使得可以有效地计算势函数和由此产生的加速度作为卫星的笛卡尔坐标 $(x,y,z)$ 。定义，则势函数可表示为

$U=\frac{GM_{\bigoplus}}{R_{\bigoplus }}\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}(C_{nm}V_{nm}+S_{nm}W_{nm})$

$V_{nm},W_{nm}$ 满足迭代关系

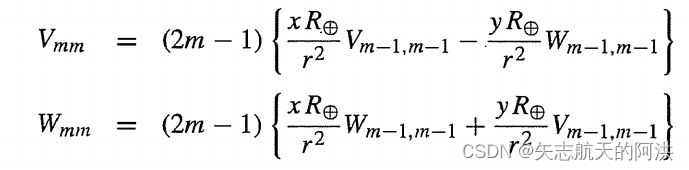
根据上述勒让德多项式和三角函数的关系。第二组方程也适用于 $n=m+1$ ，此外

$V_{00}=\frac{R_{\bigoplus} }{r},W_{00}=0$

以此求出势函数，得到加速度即为势函数对位置的偏导数

二、代码部分

根据上述理论，即可求得在地球非球形摄动影响的情况下，瞬时真地球坐标系下的加速度。根据文章（2）中求出的瞬时真天球坐标系与瞬时真地球坐标系的坐标转换关系，求得其在地球非球形摄动下的加速度。其代码如下：

%--------------------------------------------------------------------------
% 
%  AccelHarmonic: Computes the acceleration due to the harmonic gravity
%   			  field of the central body
%
% Inputs:
%   r           Satellite position vector in the inertial system
%   E           Transformation matrix to body-fixed system
%   n_max       Maximum degree 
%   m_max       Maximum order (m_max<=n_max; m_max=0 for zonals, only)
%   CS          Spherical harmonics coefficients (un-normalized)
%
% Output:
%   a           Acceleration (a=d^2r/dt^2)
%
% Last modified:   2015/08/12   M. Mahooti
% 
%--------------------------------------------------------------------------
function a = AccelHarmonic( r, E, n_max, m_max )

global CS

r_ref = 6378.1363e3;   % Earth's radius [m]; GGM03S
gm    = 398600.4415e9; % [m^3/s^2]; GGM03S

% Body-fixed position 
r_bf = E * r;

% Auxiliary quantities
r_sqr =  dot(r_bf,r_bf);      % Square of distance
rho   =  r_ref*r_ref/r_sqr;
  
x0 = r_ref*r_bf(1)/r_sqr;     % Normalized
y0 = r_ref*r_bf(2)/r_sqr;     % coordinates
z0 = r_ref*r_bf(3)/r_sqr;

%
% Evaluate harmonic functions 
%   V_nm = (r_ref/r)^(n+1) * P_nm(sin(phi)) * cos(m*lambda)
% and 
%   W_nm = (r_ref/r)^(n+1) * P_nm(sin(phi)) * sin(m*lambda)
% up to degree and order n_max+1
%

% Calculate zonal terms V(n,0); set W(n,0)=0.0
V(1,1) = r_ref/sqrt(r_sqr);
W(1,1) = 0;
      
V(2,1) = z0 * V(1,1);
W(2,1) = 0;

for n=2:n_max+1
  V(n+1,1) = ( (2*n-1) * z0 * V(n,1) - (n-1) * rho * V(n-1,1) )/n;
  W(n+1,1) = 0;
end

% Calculate tesseral and sectorial terms 

for m=1:m_max+1
    
  % Calculate V(m,m) .. V(n_max+1,m)
  V(m+1,m+1) = (2*m-1) * ( x0*V(m,m) - y0*W(m,m) );
  W(m+1,m+1) = (2*m-1) * ( x0*W(m,m) + y0*V(m,m) );

  if m<=n_max
    V(m+2,m+1) = (2*m+1) * z0 * V(m+1,m+1);
    W(m+2,m+1) = (2*m+1) * z0 * W(m+1,m+1);
  end

  for n=m+2:n_max+1
    V(n+1,m+1) = ( (2*n-1)*z0*V(n,m+1) - (n+m-1)*rho*V(n-1,m+1) ) / (n-m);
    W(n+1,m+1) = ( (2*n-1)*z0*W(n,m+1) - (n+m-1)*rho*W(n-1,m+1) ) / (n-m);
  end

end

%
% Calculate accelerations ax,ay,az
%
ax = 0;
ay = 0;
az = 0;

for m=1:m_max+1
  for n=m:n_max+1
    if (m==1) 
      C = CS(n,1);   % = C_n,0
      ax = ax - C * V(n+1,2);
      ay = ay - C * W(n+1,2);
      az = az - (n)*C * V(n+1,1);
    
    else  
      C = CS(n,m);   % = C_n,m 
      S = CS(m-1,n); % = S_n,m 
      Fac = 0.5 * (n-m+1) * (n-m+2);
      ax = ax  + 0.5 * ( - C * V(n+1,m+1) - S * W(n+1,m+1) )...
              + Fac * ( + C * V(n+1,m-1) + S * W(n+1,m-1) );
      ay = ay  + 0.5 * ( - C * W(n+1,m+1) + S * V(n+1,m+1) )...
              + Fac * ( - C * W(n+1,m-1) + S * V(n+1,m-1) );
      az = az + (n-m+1) * ( - C * V(n+1,m)   - S * W(n+1,m) );
    end
  end
end

% Body-fixed acceleration
a_bf = (gm/(r_ref*r_ref))*[ax,ay,az]';

% Inertial acceleration 
a = E'*a_bf;

矢志航天的阿洪

关注

4
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
最小二乘法的状态转移方程（3）

在关于未受扰动的开普勒运动的导言一章中，假设地球的总质量集中在坐标系的中心和引力因此，可以用来计算卫星在处所感受到的加速度。为了讨论一个更现实的模型，方便地使用涉及相应重力势梯度的等价表示。通过总结单个质量元素的贡献，这个势的表达式可以很容易地推广到任意的质量分布，取一体积微元，其表达式为，则得到每一体积微元的势函数表达式可以写为这里表示地球内部某个点的密度，是卫星到这个地方的距离球形谐波的展开为了求出上述方程的积分，将距离的导数可以展开为一系列的勒让德多项式。对于。
复制链接

扫一扫