谈谈你对线弹性断裂力学和弹塑性断裂力学的认识
经过对本课程的学习,我首先认识到断裂力学研究的是宏观的断裂问题,而不是研究属于断裂物理研究范围的微观结构断裂机理。断裂力学从材料内部存在缺陷出发,研究裂纹的生成、亚临界拓展,以及断裂的开始、传播和停止。应该从宏观上把握断裂力学研究的内容。而从学科的角度看,断裂力学是对材料力学的发展与充实,断裂力学再大量实验基础上研究带裂纹材料的断裂韧度,探究了带裂纹构件在各种工作条件下裂纹的扩展、失稳和止裂的规律,并应用这些规律设计更加安全可靠的产品。
线弹性断裂力学是断裂力学的一个重要分支,它用弹性力学的线性理论对裂纹体进行力学分析,并采用由此求得的某些特征参量(如应力强度因子、能量释放率)作为判断裂纹扩展的准则。
早在1921年,英国的格里菲思就根据裂纹体的应变能,提出了裂纹失稳扩展准则──格里菲思准则,它可以解释为什么玻璃实际断裂强度比理论值低得多,由此还可得到裂纹体能量释放率的概念,这一概念后来成为线弹性断裂力学的基本概念之一。1957年,美国的G.R.欧文通过分析裂纹顶端附近区域的应力场,提出应力强度因子的概念,并建立了以应力强度因子为参量的裂纹扩展准则,从而成功地解释了低应力脆断事故。此后不久,又有人应用应力强度因子来处理疲劳裂纹扩展等其他有关裂纹的问题。
按线弹性力学求得的裂纹体的应力和应变通常是有奇异性的,即在裂纹顶端处的应力和应变为无穷大。这在物理上是不合理的。实际上,裂纹顶端附近的应力和应变很大,线弹性力学在裂纹顶端不适用。一般说,这些区域的情况很复杂,很多微观因素(如晶粒大小、位错结构等)对裂纹顶端应力场影响很大。线弹性断裂力学不考虑裂纹顶端的复杂情况,而采用裂纹顶端外部区域的应力状况来表征断裂特性。当外加载荷不大时,裂纹顶端附近一个小区域内的应力和应变的变化并不影响外面大区域内的应力和应变的分布,而且在小区域外围作用的应力、应变场可以由应力强度因子这个参量确定。对于这种载荷作用下裂纹的失稳和扩展,线弹性断裂力学是适用的。
线弹性断裂力学适用的载荷值根据经验可以由下面两个不等式确定:
 (1)
(1)

(1)
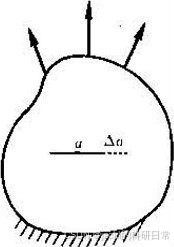
(2)
式中a为裂纹长度;B为构件厚度;σ为材料的屈服极限(见材料的力学性能);KI为在外载荷作用下,根据线弹性断裂力学计算得的应力强度因子。就是说,由外载荷算得的应力强度因子KI要满足这两个不等式。此外,在线弹性断裂力学中一般还要求在载荷下构件整体的响应是线性的。
线弹性断裂力学的几个重要理论成果如下:
图1含一长度为a的裂纹的物体
格里菲思能量准则考虑一个含一长度为a的裂纹的物体(图1),物体每单位厚度的总势能为U(a),它是裂纹长度的函数。当裂纹长度a增加时,总势能减小,可认为外力有使裂纹扩展的趋势。势能随着裂纹扩展的减小率称为裂纹扩展力或应变能释放率,记为G:

(3)
在外力作用下,裂纹虽有扩张趋势,但当外力没达到一定值时,它并不扩展;仅当外力加到一个临界值时,它才扩展。这是因为,要使裂纹扩展就要增加自由表面,从而会增加自由表面能,这相当于给裂纹扩展增加阻力。仅当有足够的表面能,裂纹才能扩展。设单位面积的表面能为γ,裂纹长度为a,则对于每单位的厚度,裂纹表面能为S=2αγ,表面能是裂纹长度a的函数。用表面能随裂纹长度的变化率可衡量裂纹扩展阻力R,即

(4)
格里菲思提出的裂纹扩展能量准则是:裂纹扩展的临界条件是裂纹扩展力等于扩展阻力,即G=R。这个准则成功地解释了玻璃的脆断问题,但用于金属并不成功。1949年,英国的E.奥罗万修正了此准则。他除了考虑表面能外,还引进了塑性功。经他修正的准则在一定程度上也能应用于金属。
应力强度因子准则这是1957年欧文提出的一个脆性断裂准则。应力强度因子是裂纹顶端附近奇异应力-应变场的一个度量参量,当它达到一个临界值时,裂纹就开始扩展。
图2外载荷和结构均以裂纹a为对称面
设外载荷和结构均以裂纹a为对称面,在裂纹顶端取坐标如图2所示。根据弹性力学的计算,在裂纹顶端附近的应力场可以近似地写成如下形式:

(5)
式中

,

为平面问题中的应力分量;

、

为极坐标。上式在

很小的情况下,近似程度是很高的。从上式中可以看出:当r→0时,应力无限增大。式中的

与坐标

、

无关,是结构形式和外载荷等的函数,它是控制裂纹应力场的系数。欧文选用此量作为判断是否断裂的一个参量,称为应力强度因子。于是裂纹扩展的临界条件为

,其中

为材料的平面应变断裂韧度,可由试验测定(见断裂试验),而KI可由弹性力学的方法求得。平面应变断裂韧度是反映物体断裂特性的重要参量,它的测定是断裂力学的基本内容。因为平面应变状态是实际工程结构中最危险的工作状态,所以平面应变断裂韧度是工程安全设计的重要参量。
复合型断裂准则在一般情况下,应力场对于裂纹面来说并不是对称分布的。但是,总可以把它分解为对称部分和反对称部分。反对称部分又可以分为面内和面外的(或称反平面的)两部分。根据对称部分的应力场可以定义应力强度因子

;对于反对称的面内和面外两部分的应力场可以定义

和

。通常相应于

、

的裂纹形式分别称为张开型、剪切型。
弹塑性断裂力学是断裂力学的一个新分支,它用弹性力学和塑性力学的理论研究变形体中裂纹的扩展规律。弹塑性断裂力学在焊接结构的缺陷评定、核电工程的安全性评定、压力容器的断裂控制以及结构物的低周疲劳和蠕变断裂的研究等方面起着重要的作用。
断裂力学的一个新分支,它用弹性力学和塑性力学的理论研究变形体中裂纹的扩展规律。弹塑性断裂力学在焊接结构的缺陷评定、核电工程的安全性评定、压力容器的断裂控制以及结构物的低周疲劳和蠕变断裂的研究等方面起着重要的作用。
20世纪中叶,由于韧性材料的广泛应用,原有的线弹性断裂力学已不能用来描述裂纹体内出现较大塑性区时裂纹的扩展规律,弹塑性断裂力学就是在此背景下发展起来的。60年代初,美国的G.R.欧文对线弹性断裂力学作了塑性修正,把它推广应用于弹塑性裂纹体,并在小范围屈服的条件下得到较好的结果。随后,英国的A.A.韦尔斯提出了在大范围屈服以至全面屈服条件下的裂纹张开位移理论(见COD法)。该理论用裂纹顶端的张开位移δ为控制参量来表示韧性断裂过程的特征,并以δ达到裂纹顶端张开位移的临界值δc为断裂准则进行断裂分析。韦尔斯的研究结果在某些缺陷评定标准中得到采用。1968年美国的J.R.赖斯提出了J积分。同年,J.W.哈钦森、J.R.赖斯和G.F.罗森格林用塑性全量理论分析了裂纹体在张开型断裂(见断裂力学)情况下裂纹顶端起裂前的应力场和应变场,并指出,在一定条件下,弹塑性体的裂纹顶端附近存在称为HRR奇异场的应力应变场,而J积分正是表征该奇异应力应变场强度的主导参量。近年来以J积分为特征参量的弹塑性断裂力学的工程方法得到了发展。
目前,弹塑性断裂力学的研究内容主要有:①确定表示韧性断裂过程中裂纹顶端场及其特征的控制参量;②发展确定裂纹扩展阻力特征的实验技术;③寻求弹塑性断裂准则。弹塑性断裂力学虽取得了一定的进展,但其理论迄今仍不成熟。
1.1国际上断裂力学的发展
早在1921年Griffith在研究玻璃断裂的问题时,提出了能量释放率准则,奠定了断裂力学的基础.在20世纪50年代航空结构脆断与高强度钢的使用,工程提出了定量分析断裂的要求.Irwin在1957年提出了应力强度因子的断裂准则;1968年Rice和Hutchinson揭示了弹塑性裂纹尖端的奇异场理论(Hutchinson--RiceRosen-grenfield,HRR场)和J积分,奠定了弹塑性断裂力学的基础.1960年Wells在实验的基础上,提出了以裂纹张开位移作为韧性断裂的控制参量,Barenblatt提出内聚区断裂模型。经五十多年的发展,宏观断裂力学已发展成一个独立的学科分支.对材料的强韧化和保证结构的安全等方面,起了十分重要的作用.当人们深入追溯断裂的原因,探求细微观的断裂过程并从力学的角度进行研究的时候,宏微观断裂力学得以发展.具体的描述可参考文献。[3-7]
1.2断裂力学在我国的发展
公元550年,学者刘子在《慎隙》文中指出:“墙之崩颓,必因其隙;剑之毁折,皆由于璺”.即墙之崩坏颓散,是因为有间隙;剑的毀坏折断,皆由于裂纹之故.明确指出裂纹会引起结构与工具的断裂破坏.近代以来,我国的断裂力学的发展,在国际上已经占有一席之地.20世纪40年代,李四光出版的专著《地质力学之基础与方法》中应用Griffith的断裂理论以解释地质学中断层运动与地震现象.1972年起,由于航空工业的发展,冶金部钢铁研究总院成立了断裂力学研究组,从测试材料的断裂韧性开始,研究工作涉及线弹性断裂力学、非线性断裂力学和疲劳裂纹扩展等领域[3].与此同时,国内多个单位相继开展了断裂力学的研究,发起并组织了1971年全国第一次断裂力学学术讨论会.迄今有“材料疲劳与断裂”、“非线性连续介质力学”等国家重点实验室和有关教育部重点实验室为骨干的实验室和几十个研究单位从事断裂的研究与应用.据不完全统计,21世纪初,我国从事断裂力学和与断裂有关的研究与实验的有2000多人.从20世纪70年代以来,中国力学学会、航空学会、机械工程学会、金属学会等学会发起与组织召开全国断裂会议,各相关的全国性学会轮流主持,每2∼3年召开一次全国性的断裂与疲劳的全国性学术大会,至2014年已连续举行了17届.我国断裂与疲劳的研究,多年来已经形成了有组织地开展科学研究与学术交流的好传统,国家自然科学基金委员会及相关的工业部门也提供了持续的经费与政策的支持.我国于1977年成为国际断裂大会(InternationalConferenceonFracture,ICF)的成员,1983年,在北京,国内外断裂大会举办了国际断裂研讨会,首次邀请了国际断裂界的近百位代表,开展断裂力学的国际学术交流.多年来,许多中国学者先后担任ICF的主席、副主席和执委.在协作研究的基础上,我国推出了多项国家标准《在用含缺陷压力容器的安全评定(GB/T19624-2004)》等和《压力容器缺陷评定规范(CVDA-1984)》的指导性文件[9].并相继推出了“KR阻力曲线”,“疲劳裂纹扩展”等多项技术指导性文件.如文献[10]所指,20世纪我国断裂研究取得许多重要的成果.如:裂纹钝化模型;岩石断裂分形几何研究;高速动态裂纹扩展;材料扩展裂纹尖端的奇异场;考虑剪切变形的含裂纹板壳理论;断裂力学的权函数方法;三维应力强度因子的变分解法;断裂力学的积分方程方法求解;相变陶瓷的剪切塑性增韧机制;非平衡统计断裂力学等.。21世纪以来,断裂研究又取得许多具有重要影响的研究成果[7]:连续力学与原子尺度的断裂分析的连接;纳观以至原子尺度界面断裂过程的实验观察;固体微尺度断裂研究;电致失效力学;电磁固体的变形与断裂,功能材料与结构的多场效应与破坏理论;压电和电磁机敏材料及结构力学行为的基础研究;超高温条件下复合材料的热致损伤机理和失效行为;岩石破裂过程失稳理论及其工程应用,破断岩体表面形貌与力学行为研究等。21世纪以来,随着信息时代的到来,新材料包括纳米材料、智能材料等得到广泛关注,断裂力学向着细-微-纳观方向拓展。
下面列举比较重要的研究方面:智能材料的断裂与损伤:出版了《力电失效学》等多本研究专著,介绍了力-电-磁-热等耦合的变分原理、本构关系、椭球体基本解、断裂行为的理论分析和实验力学测量;微纳尺度断裂力学:提出新的改进型的广变梯度理论.在《结构完整性评价大全》第8卷中对微纳米尺度的断裂力学进行了总结,其中涵盖我国学者的工作贡献;非均匀材料的断裂和损伤力学:含微裂纹准脆性材料的损伤力学与计算力学,功能梯度材料的断裂与裂纹扩展;断裂力学的试验与工程应用:多轴-多功能力-电-磁耦合试验机的研制,界面损伤与开裂的识别方法,骨裂纹尖端压电电位分布,应用塑性极限分析与安全理论,提出体积型缺陷的安全评定方法.2013年6月在北京召开的第13届国际断裂大会(The13thInternationalConferenceonPracture,ICF13),汇集与检阅了当今国内外断裂的理论与应用的成果.第13届国际断裂大会于2013年6月16日—21日在北京国家会议中心隆重召开.此次大会是中国自1977年加入国际断裂学会以来,首次承办该组织的最高级别会议,也是该系列会议首次在发展中国家举行.来自世界40余个国家和地区的近千名代表参加了会议.本次大会由国际断裂学会(In-ternationalCongressonFracture,ICF)主办,中国力学学会、香港断裂组、中国机械工程学会、中国材料研究学会、中国腐蚀与防护学会、中国航空学会、中国结构完整性联盟、中国金属学会联合承办,中国科协、国家自然科学基金委员会以及中国科学院力学研究所、清华大等支持与协办.国际断裂大会是断裂学科领域最高级别的学术会议,其内容涉及断裂学科的方方面面.本届大会共收到投稿1216篇,到会宣讲近800篇会议为期5天,分为15篇大会特邀报告、54个主题论坛和15个专题研讨会,较为全面地展示了断裂学科领域的最新研究进展和成果.大会特别邀请到一批最具国际影响力的学术大师参会交流,他们是:J积分的提出者、哈佛大J.R.Rice教授,Paris公式的提出人、华盛顿大学路易斯分校PaulC.Paris教授,HRR场的提出者之一、哈佛大学JohnW.Hutchinson教授,美国国家自然科学基金委员会前任主席、卡内基梅隆大学SubraSuresh教授,澳大利亚科学院和工程院院士、悉尼大学Yiu-WingMai教授等.中国学者杨卫院士、孙庆平教授、孙军教授也应邀作了大会特邀报告。
目前,应用于断裂力学问题数值计算的方法除了已知有限单元法,边界元法,叠加法与求解技术的几种,其他的方法也层出不穷、超奇异积分方程法、加权余量法、有限差分法、边界配置法等等,在解决断裂力学闯题时都有不同程度的应用。计算机科学、计算力学和力学学科的发展都将推动着计算断裂力学的不断发展。可以预测,今后断裂力学的数值计算将会在以下方面有更新的突破。
2.1并行数值计算方法
并行计算方法是在工程计算规模的大幅度提高与计算机的运算速度受到限制的矛盾日益突出的情况下产生和发展起来的。并行技术和并行算法的应用,将对计算断裂力学算法研究等一系列问题产生重大影响,也必将为断裂力学应用于工程实践扫除一大障碍。
2.2解析法与数值法的结合
计算机软硬件的飞速发展为计算断裂力学的发展提供了有力的工具,但是计算效率高、存储占用少的有效算法仍是研究的重点,解析法与数值方法互相交叉、渗透和结合将为断裂力学研究提供一系列高效算法。现在已经有多种有效的解析法与数值解结合的方法在结构计算中得到了广泛的应用。
- 一个J积分实例
断裂力学中有三个基本参数,即应力强度因子K,路径无关积分(J积分)和应变能释放率G,对于线弹性材料而言,这三个参数完全可以通过材料参数联系起来,并且J积分和应变能释放率是等价的(7-9)。王跃(10)等建立了简易解析模型,对单面修补直板或圆柱形弯曲板结构施加面内载荷或面外载荷,研究不同复合材料补片参数下裂纹尖端的J积分,为补片设计提供理论依据。
单面修补含中心穿透裂纹板结构的示意图如图1所示。基板和胶层为各向同性材料,补片的铺层方式为正交铺层,
方向与裂纹方向垂直,为类各向同性材料。
图1复合材料单面修补含裂纹板结构
根据施加的轴力和弯矩求取基板应力,再由承受面内载荷的基板应力
、
,求得平均轴应力和平均弯曲应力为:
(6)
对于上述给定的公式,应用了基板最小应力的绝对值。这是为了说明裂纹闭合的作用,如果有一个负的最小应力,即压应力,则会造成局部裂纹面的闭合,裂纹尖端的J积分减小。
J积分通常用来表示裂纹尖端应力集中程度的断裂参数。裂纹板贴补复合材料补片后,J积分受应力
和
的作用,轴向力
是产生轴向变形的应力分量,而弯曲应力是导致修补板产生弯曲变形的应力分量。由轴向应力和弯曲应力得到的应力强度因子以及单面修补裂纹板的J积分与应力强度因子的平方成正比,得到:
(7)
式中,
是要确定的比例常数。上式表达了上述单面搭接接头模型中由正则化轴向应力和弯曲应力的平方得到的修补板正则化J积分的比率,为选择合适的补片厚度和材料属性的组合提供了依据。J积分比率表明了修补后裂纹尖端J积分值的减小程度。例如,若J积分比率值为0.5,意味着由于补片的作用,J积分值减少了一半。
根据施加的轴力和弯矩求取基板应力。基板层中的最大和最小正应力可由图3中的自由体简图求得,图3(a)承受面内载荷的基板应力为
图2复合材料单面修补结构的单搭接接头结构
图3 沿基板与补片切断后复合材料单面修补含裂纹结构的自由体简图
建立修补结构的三维有限元模型研究补片的长度和宽度对修补板裂尖端J积分的影响。使用适合弹塑性分析的C3D20R单元对金属板进行建模,使用Counter型裂纹模拟穿透裂纹损伤,获得裂纹尖端J积分。图2为承受面内载荷含不同裂纹长度修补板裂纹尖端J积分变化曲线。可以看出,随着补片长度的增肌,J积分逐渐减小,当补片长度超过裂纹长度两倍后,J积分基本成为一常数。而J积分与补片宽度的函数关系如图3所示,曲线的形状与J积分随补片长度的变化趋势相同。
图2面内载荷下复合材料单面修补结构裂纹尖端J积分随补片长度变化曲线
图3面外载荷作用下复合材料单面修补结构裂纹尖端J积分随补片宽度变化曲线
为了验证式(6)的有效性,利用有限元计算不同裂纹尺寸、补片厚度和模量下的正则化的J积分,即式(6)的左部,利用式(7)的右部求解不同补片厚度和模量下正则化的应力的二次方。利用有限元模型对各类型的补片进行研究,总共两种基板厚度:3mm和5mm,两种裂纹长度:50.8mm和101.6mm,9种弹性模量和9种补片厚度。
图4面内载荷下不同厚度和属性的复合材料补片修补两类裂纹长度平板后正则化J积分与正则化应力平方的对应关系
面内载荷条件下正则化J积分和应力值平方的对应关系如图4所示,进行两者的线性拟合。可以看出,式(7)的预测与有限元结果吻合的较好,因此在给定某一裂纹板后,可以利用式(7)对补片的模量和厚度进行优化选择。
另外,在考虑宽度效应对J积分的影响时,由数据拟合和正则化方法,可得修正后的J积分与应力强度因子的平方的关系:
(8)
综上所述,如果单面修补的平板承受面内载荷,仅用式(8)就可以对修补结构J积分进行预测,而在平板承受面外载荷或者圆柱形弯曲板的情况,使用式(7)考虑补片。
结论:利用单搭接接头解析模型和有限元模型的结果,对J积分解析方程的系数进行了拟合求解,该方程适用于施加面内载荷、面外载荷以及混合加载方式的直板和弯曲板。当平板承受面外载荷或基板为弯曲板时,求解J积分的解析方程要根据宽度效应方程进行修正。
参考文献:
1. 赵建生. 断裂力学及断裂物理: 华中科技大学出版社; 2003.
2. Dally J, Fourney W, Irwin G. On the uniqueness of the stress intensity factor—crack velocity relationship. International Journal of Fracture. 1985;27(3-4):159-68.
3. Erdogan F, Sih G. On the crack extension in plates under plane loading and transverse shear. 1963.
4. Palaniswamy K. Crack propagation under general in-plane loading: California Institute of Technology; 1972.
5. Sih GC. Strain-energy-density factor applied to mixed mode crack problems. International Journal of fracture. 1974;10(3):305-21.
6. Sih G. Some basic problems in fracture mechanics and new concepts. Engineering fracture mechanics. 1973;5(2):365-77.
7. Albedah A, Bachir Bouiadjra B, Ouddad W, Es-Saheb M, Binyahia F. Elastic plastic analysis of bonded composite repair in cracked aircraft structures. Journal of reinforced plastics and composites. 2011;30(1):66-72.
8. Oudad W, Bouiadjra BB, Belhouari M, Touzain S, Feaugas X. Analysis of the plastic zone size ahead of repaired cracks with bonded composite patch of metallic aircraft structures. Computational Materials Science. 2009;46(4):950-4.
9. Fekih S, Albedah A, Benyahia F, Belhouari M, Bouiadjra BB, Miloudi A. Optimisation of the sizes of bonded composite repair in aircraft structures. Materials & Design. 2012;41:171-6.
10. 王跃, 穆志韬, 刘治国. 复合材料单面修补板裂纹尖端J积分的解析预测模型. 复合材料学报. 2018;35(02):332-9.

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










