利用 MATLAB 编程实现 Newton 法与阻尼 Newton 法

本文章包含以下内容

1、画出阻尼 Newton 法的算法流程图；

2、MATLAB 编写用数值微分计算二阶 Hesse 矩阵的函数（函数式 M 文件）；

3、MATLAB 编写 Newton 法求解无约束优化问题的函数，用数值微分计算 二阶 Hesse 矩阵（函数式 M 文件，精度设为 epson 可调）；

4、MATLAB 编写阻尼 Newton 法求解无约束优化问题的函数，要求采用 黄金分割法精确一维搜索，用数值微分计算 Hesse 矩阵（函数式 M 文件，精 度设为 epson 可调）；

5、MATLAB 编写阻尼 Newton 法求解无约束优化问题的函数，要求采用 Wolfe-Powell 非精确一维搜索，用数值微分计算 Hesse 矩阵（函数式 M 文件， 精度设为 epson 可调）；

6、MATLAB 编写程序（命令式 M 文件），分别利用 Newton 法、精确搜索与 不精确搜索的阻尼 Newton 法，求解如下问题：

精度为 0.001，初始点为（-1，1）。

数值微分法，Wolfe-Powell 非精确一维搜索代码链接

一维搜索，进退法，黄金分割法代码链接

本实验中函数用单独function计算

function y=f(x)
if(length(x)==1)
    global xk;
    global pk;
    x=xk+x*pk;
end
y=100*(x(2)-x(1)^2)^2+(1-x(1))^2;

1、阻尼 Newton 法的算法流程图；

 

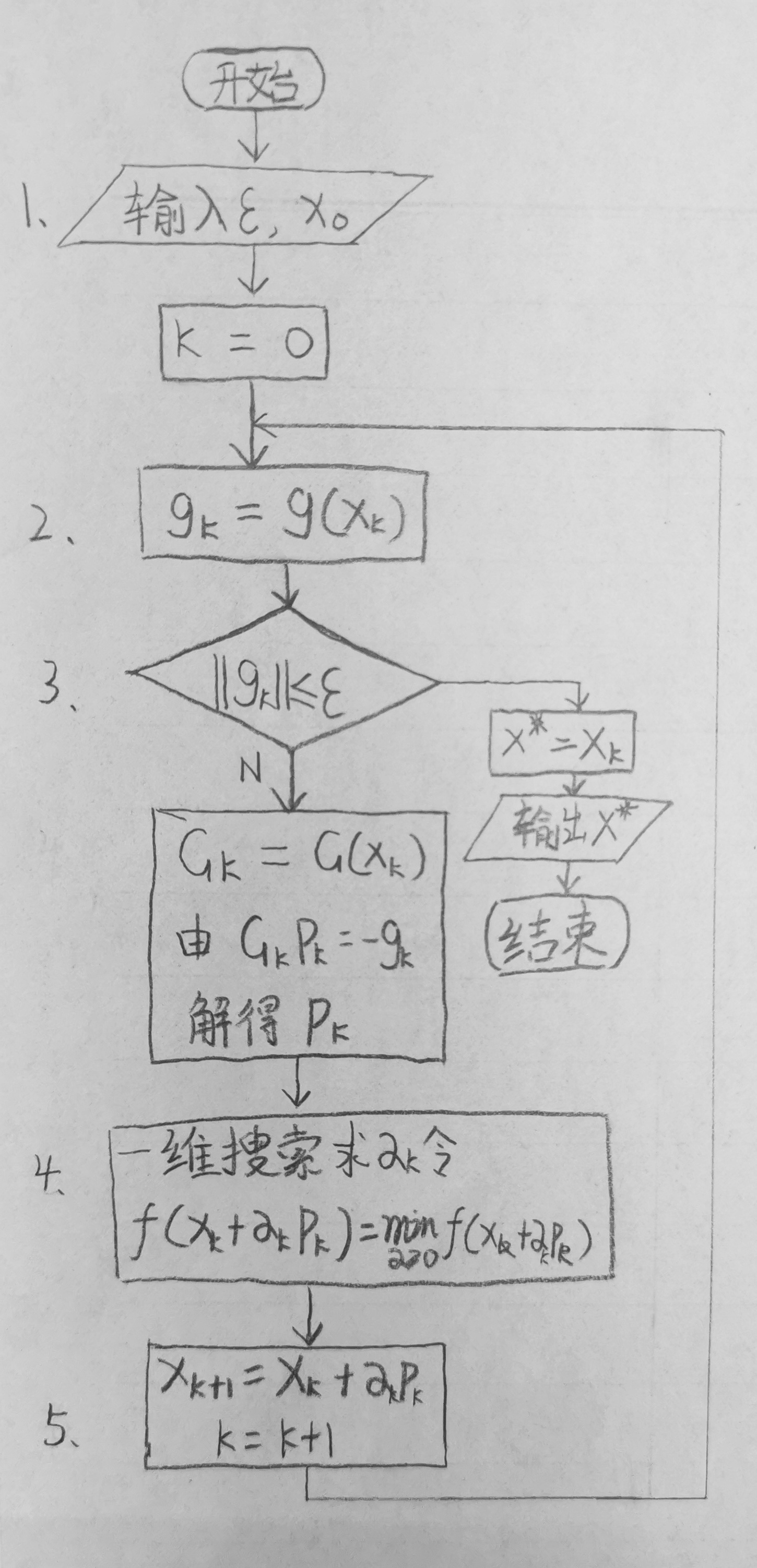
2、MATLAB 编写用数值微分计算二阶 Hesse 矩阵的函数（函数式 M 文件）；

function G=Hesse_2(x)
fx=f(x);%避免多次计算
G=zeros(length(x));
for i = 1 : length(x)
    for j = 1 : length(x)
        if i == j
            m=zeros(1,length(x));
            m(i)=(10^-6);
            G(i,i)=(f(x+m)+f(x-m)-2*fx)/(10^-12);
        else
            m=zeros(1,length(x));
            m(i)=(10^-6);
            n=zeros(1,length(x));
            n(j)=(10^-6);
            G(i,j)=(f(x+m+n)-f(x+m)-f(x+n)+fx)/(10^-12);
        end
    end
end

3、MATLAB 编写 Newton 法求解无约束优化问题的函数，用数值微分计算 二阶 Hesse 矩阵（函数式 M 文件，精度设为 epson 可调）；

function xk=Newton(e,xk)
%step 1
%没用到k，只存储当前迭代的值。
while 1
    %step 2
    gk=shuzhiweifenfa(xk);
    %step 3
    %范数用的是平方和开根号
    if sqrt(sum(gk.^2))<=e
        return
    end
    Gk=Hesse_2(xk);
    %由于之前函数默认返回行向量
    %gk需转置
    pk=-Gk^-1*gk';
    %step 4
    xk=xk+pk';
end

4、MATLAB 编写阻尼 Newton 法求解无约束优化问题的函数，要求采用 黄金分割法精确一维搜索，用数值微分计算 Hesse 矩阵（函数式 M 文件，精 度设为 epson 可调）；

function xk=Newton_hjfg(e,x)
global xk;
global pk;
xk=x;
%step 1
%没用到k，只存储当前迭代的值。
while 1
    %step 2
    gk=shuzhiweifenfa(xk);
    %step 3
    %范数用的是平方和开根号
    if sqrt(sum(gk.^2))<=e
        return
    end
    Gk=Hesse_2(xk);
    %由于之前函数默认为行向量
    %pk,gk需转置
    pk=(-Gk^-1*gk')';
    %step 4
    %一维搜索求ak
    %这两个函数见之前代码（matlab无约束最优化的一般算法）
    [a,b,c]=jintuifa(0,0.1);
    a=huangjinfenge(a,c,10^-4);
    %step 5
    xk=xk+a*pk;
end

5、MATLAB 编写阻尼 Newton 法求解无约束优化问题的函数，要求采用 Wolfe-Powell 非精确一维搜索，用数值微分计算 Hesse 矩阵（函数式 M 文件， 精度设为 epson 可调）；

function xk=Newton_Wolfe(e,x)
global xk;
global pk;
xk=x;
%step 1
%没用到k，只存储当前迭代的值。
while 1
    %step 2
    gk=shuzhiweifenfa(xk);
    %step 3
    %范数用的是平方和开根号
    if sqrt(sum(gk.^2))<=e
        return
    end
    Gk=Hesse_2(xk);
    %由于之前函数默认为行向量
    %pk,gk需转置
    pk=(-Gk^-1*gk')';
    %step 4
    %一维搜索求ak
    %函数见之前代码（利用 MATLAB 编程实现最速下降法求解无约束最优化问题）
    a=Wolfe_Powell(xk,pk);
    %step 5
    xk=xk+a*pk;
end

6、MATLAB 编写程序（命令式 M 文件），分别利用 Newton 法、精确搜索与 不精确搜索的阻尼 Newton 法，求解如下问题：

精度为 0.001，初始点为（-1，1）。

clear
clc
x=[-1,1];
fprintf('=========================');
fprintf('\nx=%f\t\t%f\n',x(1),x(2));
fprintf('=========================\n');
fprintf('Newton 法:\n');
x_=Newton(10^-3,x);
fprintf('x*=%f\t%f\n',x_(1),x_(2));
fprintf('f(x)=%f\n',f(x_));
fprintf('精确搜索的阻尼 Newton 法:\n');
x_=Newton_hjfg(10^-3,x);
fprintf('x*=%f\t%f\n',x_(1),x_(2));
fprintf('f(x)=%f\n',f(x_));
fprintf('不精确搜索的阻尼 Newton 法:\n');
x_=Newton_Wolfe(10^-3,x);
fprintf('x*=%f\t%f\n',x_(1),x_(2));
fprintf('f(x)=%f\n',f(x_));

结果：