该实验旨在通过可变式分区管理方法，使用最佳或首次适应算法来分配和回收主存空间。实验内容包括初始化分区、空闲区管理、作业的装入和释放。提供的C语言代码实现了分配和回收过程，包括分区的合并和分割。实验结果表明，各种回收情况均能得到有效处理。
一、实验题目
采用可变式分区管理，使用最佳适应算法实现主存的分配与回收
二、实验内容
主存是中央处理机能直接存取指令和数据的存储器。能否合理而有效地使用主存，在很大程度上将影响到整个计算机系统的性能。本实验采用可变式分区管理，使用首次或最佳适应算法实现主存空间的分配与回收。要求采用分区说明表进行。
三、实验目的
通过本次实验，帮助学生理解在可变式分区管理方式下，如何实现主存空间的分配与回收。
提示：
1.可变式分区管理是指在处理作业过程中建立分区，使分区大小正好适合作业的需要，并且分区个数是可以调整的。当要装入一个作业时，根据作业需要的主存量，查看是否有足够的空闲空间，若有，则按需求量分割一部分给作业；若无，则作业等待。随着作业的装入、完成，主存空间被分割成许多大大小小的分区。有的分区被作业占用，有的分区空闲。例如，某时刻主存空间占用情况如图1所示。
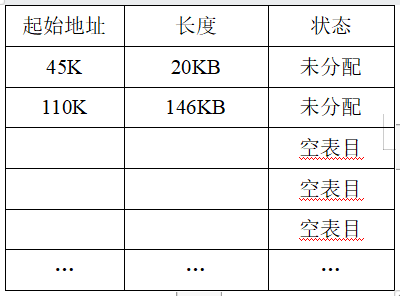
为了说明哪些分区是空闲的，可以用来装入新的作业，必须要有一张空闲区说明表，如表1所示。
其中，起始地址指出各空闲区的主存起始地址，长度指出空闲区大小。状态栏未分配指该栏目是记录的有效空闲区，空表目指没有登记信息。由于分区个数不定，所以空闲区说明表中应有足够的空表目项，否则造成溢出，无法登记。同样，再设一个已分配区表，记录作业或进城的主存占用情况。
当有一个新作业要求装入主存时，必须查空闲区说明表，从中找出一个足够大的空闲区。有时找到的空闲区可能大于作业需求量，这时应该将空闲区一分为二。一个分给作业，另一个仍作为空闲区留在空闲区表中。为了尽量减少由于分割造成的碎片，尽可能分配低地址部分的空闲区，将较大空闲区留在高地址端，以利于大作业的装入。为此在空闲区表中，按空闲区首地址从低到高进行登记。为了便于快速查找，要不断地对表格进行紧缩，即让“空表目”项留在表的后部。其分配框图如图2所示。
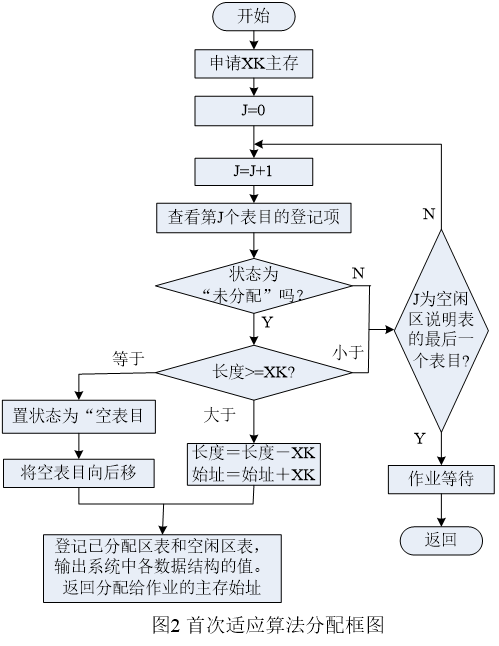
（3）当一个作业执行完时，作业所占用的分区应归还给系统。在归还时要考虑相邻空闲区合并的问题。作业的释放区与空闲区的邻接分一下4种情况考虑：
A．释放区下邻（低地址邻接）空闲区；
B．释放区上邻（高地址邻接）空闲区；
C．释放区上下都与空闲区邻接；
D．释放区与空闲区不邻接。
首次适应算法回收框图如图3所示。
若采用最佳适应算法，则空闲区说明表中的空闲区按其大小排序。有关最佳适应算法的分配和回收框图由学生自己给出。
（4）请按首次（或最佳）适应算法设计主存分配和回收程序。以图1作为主存当前使用的基础，初始化空闲区和已分配区说明表的值。学生自己设计一个作业申请队列以及作业完成后的释放顺序，实现主存的分配与回收。把空闲区说明表的变化情况以及各作业的申请、释放情况显示或打印出来。
为了说明哪些分区是空闲的，必须要有一张空闲区说明表，格式如下表所示：
四、实验结果
源代码：
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <termio.h>
//#include <curses.h>
#define MAX 600 //设置总内存大小为512k
struct partition {
char pn[10];//分区名字
int begin;//起始地址
int size;//分区大小
int end;//结束地址
char status;//分区状态
};
struct partition part[MAX];
int p = 0; //标记上次扫描结束处
void Init()//初始化分区地址、大小以及状态
{
int i;
for ( i = 0; i < MAX; i++ )
part[i].status = '-';
strcpy( part[0].pn, "SYSTEM" );
part[0].begin = 0;
part[0].size = 100;
part[0].status = 'u';
strcpy( part[1].pn, "-----" );
part[1].begin = 100;
part[1].size = 100;
part[1].status = 'f';
strcpy( part[2].pn, "作业1" );
part[2].begin = 200;
part[2].size = 50;
part[2].status = 'u';
strcpy( part[3].pn, "-----" );
part[3].begin = 250;
part[3].size = 50;
part[3].status = 'f';
strcpy( part[4].pn, "作业2" );
part[4].begin = 300;
part[4].size = 100;
part[4].status = 'u';
strcpy( part[5].pn, "-----" );
part[5].begin = 400;
part[5].size = 200;
part[5].status = 'f';
for ( i = 0; i < MAX; i++ )
part[i].end = part[i].begin + part[i].size-1;
}
void Output( int i ) //以行的形式输出结构体的数据
{
printf( "\t%s", part[i].pn );
printf( "\t%d", part[i].begin );
printf( "\t%d", part[i].size );
printf( "\t%d", part[i].end );
printf( "\t%c", part[i].status );
}
void display() //显示分区
{
int i;
int n; //用n来记录分区的个数
printf("\n");
printf( "\n 已分配分区表Used:" );
printf( "\n\tNo.\tproname\tbegin\tsize\tend\tstatus" );
printf("\n");
n = 1;
for ( i = 0; i < MAX; i++ )
{
if ( part[i].status == '-' )
break;
if ( part[i].status == 'u' )
{
printf( "\n\tNo.%d", n );
Output( i );
n++;// 记录已分配使用的分区个数
}
}
printf("\n");
printf( "\n 空闲分区表Free:" );
printf( "\n\tNo.\tproname\tbegin\tsize\tend\tstatus" );
printf("\n");
n = 1;
for ( i = 0; i < MAX; i++ )
{
if ( part[i].status == '-' )
break;
if ( part[i].status == 'f' )
{
printf( "\n\tNo.%d", n );
Output( i );
n++; //记录空闲分区的个数
}
}
printf("\n");
printf( "\n 内存使用情况，按起始址增长的排:" );
//printf( "\n printf sorted by address:" );
printf( "\n\tNo.\tproname\tbegin\tsize\tend\tstatus" );
printf("\n");
n = 1;
for ( i = 0; i < MAX; i++ )
{
if ( part[i].status == '-' )
break;
printf( "\n\tNo.%d", n );
Output( i );
n++;//记录已分配分区以及空闲分区之和的总个数
}
}
void Fit( int a, char workName[], int workSize ) //新作业把一个分区分配成两个分区：已使用分区和空闲分区
{
int i;
for ( i = MAX; i > a + 1; i-- ){
//通过逆向遍历，把在a地址后的所有分区往后退一个分区，目的在于增加一个分区
if ( part[i - 1].status == '-' )
continue;
part[i]=part[i-1];
}
strcpy( part[a + 1].pn, "-----" );
part[a + 1].begin = part[a].begin + workSize;
part[a + 1].size = part[a].size - workSize;
part[a + 1].end = part[a].end-1;
part[a + 1].status = 'f';
strcpy( part[a].pn, workName );
part[a].size = workSize;
part[a].end = part[a].begin + part[a].size-1;
part[a].status = 'u';
}
int getch(void)
{
struct termios tm, tm_old;
int fd = 0, ch;
if (tcgetattr(fd, &tm) < 0) {//保存现在的终端设置
return -1;
}
tm_old = tm;
cfmakeraw(&tm);//更改终端设置为原始模式，该模式下所有的输入数据以字节为单位被处理
if (tcsetattr(fd, TCSANOW, &tm) < 0) {//设置上更改之后的设置
return -1;
}
ch = getchar();
if (tcsetattr(fd, TCSANOW, &tm_old) < 0) {//更改设置为最初的样子
return -1;
}
return ch;
}
void fenpei() // 分配
{
int i;
int a;
int workSize;
char workName[10];
int pFree;
printf( "\n请输入作业名称：" );
scanf( "%s", &workName );
for(i=0;i<MAX;i++){
if(!strcmp(part[i].pn,workName))//判断作业名称是否已经存在
{
printf("\n作业已经存在，不必再次分配！\n");
return;
}
}
printf( "请输入作业大小(k)：" );
scanf( "%d", &workSize );
for ( i = 0; i < MAX; i++ ){//通过循环在空闲区找是否有适合区间存储作业
if ( part[i].status == 'f' && part[i].size >= workSize ){
pFree = i;
break;
}
}
if ( i == MAX ){
printf( "\n该作业大小超出最大可分配空间" );
getch();
return;
}
for ( i = 0; i < MAX; i++ )//最佳适应算法
if ( part[i].status == 'f' && part[i].size >= workSize )
if ( part[pFree].size > part[i].size )
pFree = i;//通过遍历所有区间，每次都找到最小空闲分区进行分配
Fit( pFree, workName, workSize );
printf( "\n分配成功！" );
}
void hebing() //合并连续的空闲分区
{
int i = 0;
while ( i != MAX - 1 ){
for ( i = 0; i < MAX - 1; i++ ){
if ( part[i].status == 'f' )
if ( part[i + 1].status == 'f' ){
part[i].size = part[i].size + part[i + 1].size;
part[i].end = part[i].begin + part[i].size-1;
i++;
for ( i; i < MAX - 1; i++ ){
if ( part[i + 1].status == '-' ){
part[i].status = '-';
break;
}
part[i]=part[i+1];
}
part[MAX - 1].status = '-';
break;
}
}
}
}
void huishou() // 回收分区
{
int i;
int number;
int n=0;
printf( "\n请输入回收的分区号：" );
scanf( "%d", &number );
if ( number == 1 )
{
printf( "\n系统分区无法回收" );
return;
}
for ( i = 0; i < MAX; i++ )//通过循环查找要回收的已使用分区区号
{
if ( part[i].status == 'u' )
{
n++;
if ( n == number )
{
strcpy( part[i].pn, "-----" );
part[i].status = 'f';
}
}
}
if ( i == MAX - 1 )
{
printf( "\n找不到分区" );
return;
}
hebing();//合并连续的空闲分区
printf( "\n回收成功！" );
}
void main()
{
int selection;
Init();
printf( "初始化完成，设内存容量%dk", MAX );
printf( "\n系统文件从低址存储，占%dk", part[0].size );
while ( 1 ){
printf( "\n----------选择----------" );
printf( "\n| 0、退出系统 |" );
printf( "\n| 1、显示分区 |" );
printf( "\n| 2、分配分区 |" );
printf( "\n| 3、回收分区 |" );
printf( "\n------------------------");
printf( "\n请选择 > " );
while ( 1 )
{
scanf( "%d", &selection );
if ( selection == 0 ||selection == 1 || selection == 2 || selection == 3 )
break;
printf( "输入错误，请重新输入：" );
}
switch ( selection ){
case 0:
exit(0); //退出系统
break;
case 1:
display(); //显示分区
break;
case 2:
fenpei(); //分配作业
break;
case 3:
huishou(); //回收分区
break;
default:
break;
}
printf("\n");
}
}运行结果：
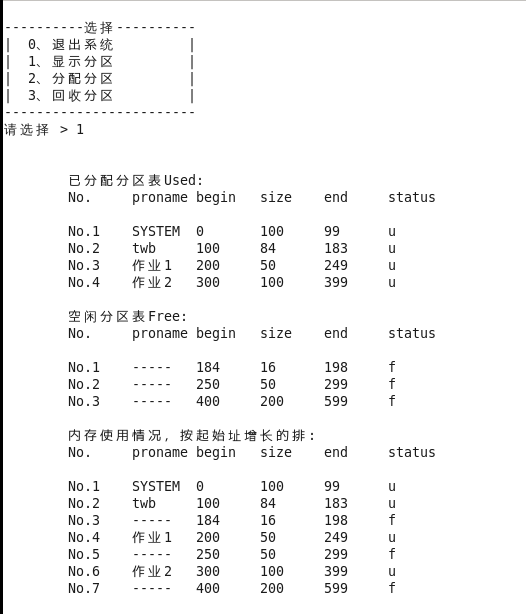
经测试，回收分区四种情况（上邻不下邻，上不邻下邻，上下都邻，上下都不邻）都可实现
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
