数值计算之数值积分与微分

程序和三三总有一个能跑

已于 2022-06-25 23:13:13 修改

阅读量2.9k

点赞数 7

文章标签： c语言

于 2022-06-25 19:05:49 首次发布

本文链接：https://blog.csdn.net/weixin_59901957/article/details/125451129

版权

一、实验内容

(1)编写用矩形法、梯形法和辛普森法求解定积分，并对三种算法的运行结果进行定性和定量的分析。

(2)请查阅文献整理求数值积分的其它方法，并至少编程实现其中的一种算法。结合（1）的结果对比分析几种算法的性能。

(3)请查阅文献整理求数值微分的其它方法，并至少编程实现其中的一种算法。

二、实验过程——数值积分

（一）函数的指针和指向函数的指针变量

一个函数在编译时被分配给一个入口地址，这个入口地址就称为函数的指针。

可以定义一个指针变量指向函数，该指针称为指向函数的指针变量。

1.定义p是指向函数的指针变量，它可以指向类型为整型且有两个整型参数的函数。

p的类型用int(*)(int,int) 表示。

函数类型（*指针变量名）(形参列表)；

括号的优先级比*高，所以第一个括号不可以少。

int (*p)(int,int);

2.指针赋值
         f=func; (func(x)必须先要有定义)
3.调用函数(x必须先赋值)
         (*指针变量)(参数表);。
         (*f)(x);

（二）数值积分概念

1.定义：

数值分析是离散点上的函数值的线性组合。

2.好一点的理解：

数值积分，用于求定积分的近似值。

在数值分析中，数值积分是计算定积分数值的方法和理论。在数学分析中，给定函数的定积分的计算不总是可行的：许多定积分不能用已知的积分公式得到精确值（利用原函数计算定积分的方法建立在Newton-Leibniz 公式之上）。然而，原函数可以用初等函数表示的函数为数不多，大部分的可积函数的积分无法用初等函数表示，甚至无法有解析表达式。

三种无法使用公式的情况：1、函数由离散数据组成 2、F(x)求不出 3、F(x)非常复杂。

3.基本思想：

积分中值定理（截图来自百度百科）

积分中值定理揭示了一种将积分化为函数值，或者是将复杂函数的积分化为简单函数的积分的方法，是数学分析的基本定理和重要手段，在求极限、判定某些性质点、估计积分值等方面应用广泛。

4.方法：

矩形法和梯形法都是用直线线段拟合函数曲线的方法，辛普森法则是采用曲线段拟合函数，实现近似逼近的数值积分方法。

（三）矩形法

1.定义

矩形法是一种计算定积分近似值的方法，其思想是求若干个矩形的面积之和，这些矩形的高由函数值来决定。

2.定长矩形法

将积分区间[a, b] 划分为n个长度相等的子区间，每个子区间的长度为(a-b)/n 。这些矩形左上角、右上角或顶边中点在被积函数上。这样，这些矩形的面积之和就约等于定积分的近似值。

从而有左定长矩形、中定长矩形、右定长矩形三个函数；

3.变长矩形法

在要求精度时我们不知道事先应该分割成多少段，分的少了精度达不到，分的多了计算量太大。为了解决这个问题，再加一层循环，不断地对区间进行再次划分，知道达到精度要求为止。变步长积分法的区间划分是成倍增加的。

步骤：

(1)将积分区间一等分，求出积分值；

(2)将每个小区间二等分，求出积分值；

(3)判断二等分前后积分值的差的绝对值，若满足精度要求则停止，否则转步骤(2)

4.代码


//定长左矩形法
//a为积分下限，b为积分上限，n为划分个数，f是指向被积函数的指针
double RintLeft(double a, double b, int n, double (*f)(double))
{
	double small = (b - a) / n;
	double ans = 0;
	for (double i = a; i <= b;)//i的初始值位积分下限
		//注意i是double，不要习惯写成int
	{
		ans += small * f(i);
		i += small;
	}
	cout << ans;
	return ans;
}

//定长中矩形法
//a为积分下限，b为积分上限，n为划分个数，f是指向被积函数的指针
double RintMiddle(double a, double b, int n, double (*f)(double))
{
	double small = (b - a) / n;
	double ans = 0;
	for (double i = a+small/2; i <= b;)//i的初始值就为中点
	{
		ans += small * f(i);
		i += small;
	}
	cout << ans;
	return ans;
}

//定长右矩形法
//a为积分下限，b为积分上限，n为划分个数，f是指向被积函数的指针
double RintRight(double a, double b, int n, double (*f)(double))
{
	double small = (b - a) / n;
	double ans = 0;
	for (double i = a; i <= b;)
	{
		i += small;
		ans += small * f(i);
		
	}
	cout << ans;
	return ans;
}


//变长矩形法
double RintChangeLeft(double a, double b, double eps, double (*f)(double))
{
	double ans = 0,Before=0,After=0;
	int n = 1;
	do
	{
		Before = After;//存储上一次
		After = 0;//记录本次
		double small = (b - a) / n;
		for (double i = a; i <= b;)
		{
			After += small * f(i);
			i += small;
		}
		n *= 2;
	} while (fabs(After - Before) >= eps);
	return After;
}

（四）梯形法

1.概念

为了计算出更加准确的定积分，采用梯形代替矩形计算定积分近似值，其思想是求若干个梯形的面积之和，这些梯形的长短边高由函数值来决定。这些梯形左上角和右上角在被积函数上。这样，这些梯形的面积之和就约等于定积分的近似值。

梯形公式要计算两个点的函数值f(a)和f(b)。所以属于两点积分。

2.同理

同理，梯形法也可以分成定长和变长；

3.代码


//定长梯形法
//a为积分下限，b为积分上限，n为划分个数，f是指向被积函数的指针
double TintRemain(double a, double b, int n, double (*f)(double))
{
	double small = (b - a) / n;
	double ans = 0;
	for (double i = a; i <= b;)
	{
		double temp = (*f)(i);
		i += small;
		temp += (*f)(i);
		ans += small / 2 * temp;
	}
	//cout << ans;
	return ans;
}

//变长梯形法
double TintChange(double a, double b, double eps, double (*f)(double))
{
	double ans = 0, Before = 0, After = 0;
	int n = 1;
	do
	{
		Before = After;//存储上一次
		After = 0;//记录本次
		double small = (b - a) / n;
		for (double i = a; i <= b;)
		{
			After += small * f(i);
			i += small;
		}
		n *= 2;
	} while (fabs(After - Before) >= eps);
	return After;
}

（五）辛普森法Simpson's rule

1.定义

辛普森法（Simpson’s rule）是以二次曲线逼近的方式取代矩形或梯形积分公式，以求得定积分的数值近似解。也称为抛物线近似法。

也是牛顿-寇次公式的特殊形式，以二次曲线逼近的方式取代矩形或梯形积分公式，以求得定积分的数值近似解。它是将区间端点和区间中点做对应的三个点近似看成抛物线上的三个点，然后利用普通的定积分法则推出公式。其近似值如下：

在小区间范围内，用一条抛物线代替该区间的f(x)，每条抛物线涵盖了两个区域一位界定两个区域的三点决定一条抛物线，使用这个方法时要求区间的个数必须为偶数。

2.同理

同理，梯形法也可以分成定长和变长；

3.代码

//定长辛普森求积法
//a为积分下限，b为积分上限，n为划分个数，f是指向被积函数的指针
double Simpson(double a, double b, int n, double (*f)(double))
{
	double x=a,ans=0;
	double height=(b-a)/n;
	double fa, fb,fab;
	for (int i = 0; i < n; i++)
	{
		fa = (*f)(x + i * height);
		fb = (*f)(x + (i + 1) * height);
		fab = (*f)(x + i * height + height / 2);
		ans += height / 6 * (fa + 4 * fab + fb);
	}
	return ans;
}

//变长辛普森求积法
//a为积分下限，b为积分上限，eps是积分精度要求，f是指向被积函数的指针
double SimpsonChange(double a, double b, double eps, double (*f)(double))
{
	double ans = 0, Before = 0, After = 0;
	double n = 1;
	double x = a;
	double fa, fb, fab;
	do
	{
		Before = After;//存储上一次
		After = 0;//记录本次
		double height = (b - a) / n;
		for (int i = 0; i < n; i++)
		{
			fa = (*f)(x + i * height);
			fb = (*f)(x + (i + 1) * height);
			fab = (*f)(x + i * height + height / 2);
			After += height / 6 * (fa + 4 * fab + fb);
		}
		n *= 2;
	} while (fabs(After - Before) >= eps);
	return After;
}

（六）龙贝格求积

1.概念

龙贝格求积公式也称为逐次分半加速法。是数值计算方法之一，用以求解数值积分。是在梯形公式、辛普森公式和柯特斯公式之间关系的基础上，构造出一种加速计算积分的方法。作为一种外推算法，在不增加计算量的前提下提高了误差的精度。

2.公式

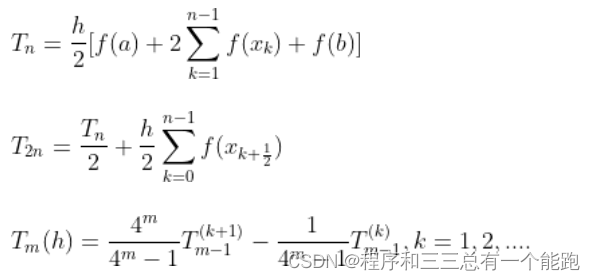
3.步骤（截图来自这里）

4.代码

//计算T//复化梯形公式
double ComputeT(double a, double b,int n, double (*f)(double))
{
	int i;
	double sum=0, h = (b- a) / n;
	for (i = 1; i < n; i++)
		sum += f(a + i * h);
	sum += (f(a) + f(b)) / 2;
	return (h * sum);
}

double Dragon(double a, double b, double eps, double (*f)(double))
{
	double T[10][2];
	long int n= 1000,m=0;
	T[0][1] = ComputeT(a, b, 20,f);
	n *= 2;
	//将区间逐次分半，加速得到积分近似值
	for (m = 1; m < 10; m++)
	{
		for (int i = 0; i < m; i++)
		{
			T[i][0] = T[i][1];
		}
		T[0][1] = ComputeT(a, b, n,f);
		n *= 2;
		//T的m(h)
		for (int i = 1; i <= m; i++) 
			T[i][1] = T[i - 1][1] + (T[i - 1][1] - T[i - 1][0]) / (pow(2, 2 * m) - 1);
		if ((T[m - 1][1] < T[m][1] + eps) && (T[m - 1][1] > T[m][1] - eps))
		{
			//输出
			return  T[m][1];
		}
		
	}return 0;
}

（七）运行结果及分析比较

1. 将积分中求原函数的问题转化为求节点处的函数值的问题，使积分问题的计算得到大大简化。

2.矩形积分的误差比梯形误差大；利用中间函数值的误差比用左右两边函数值的误差小；

3.步长越小（区间分割的份数越多），结果越精确。变步长积分的精确度更高。

4.辛普森以二次曲线逼近的方式取代矩形或梯形积分公式，比微分思想下的求定积分更精准啦，并且辛普森收敛速度更快。

5.从计算公式复杂性方面来说，龙贝格数值积分公式的计算量最少。而且不增加计算量的前提下提高了误差的精度。

6.无论是矩形、梯形公式、辛普森公式还是龙贝格积分公式，都有着较高的精度，结果近乎相同，不过相较之下，龙贝格积分公式精度最高。

三、实验过程——数值微分(numerical differentiation)

（一）数值微分概念

1.定义

根据函数在一些离散点的函数值，推算它在某点的导数或者高阶导数的近似值的方法。通常用差商代替微商，或者用一个能够近似代替该函数的较简单的可微函数（如多项式函数或样条函数等）的相应导数作为能求导数的近似值。

2.应用情况：

（1）函数由函数表给出

（2）F(x)函数的导数不易求取

2.方法：

（1）用差商求微分

（2）用插值函数求取微分

（二）用差商求微分

1.概念

在微积分学中，函数的导数是通过差商的极限来定义的，表示函数在某点的瞬时变化率，即平均变化率的极限。几何意义为曲线的斜率。

2.代码：

//数值微分
//向后差商法
//x是要求导数的点，eps是精度要求，f是指向被积函数的指针
double CDFBehind(double x, double eps, double (*f)(double))
{
	double h = 0.4;
	double y1 = ((*f)(x) - (*f)(x - h)) / h;
	double y2, temp;
	do {
		h /= 2;
		y2 = ((*f)(x) - (*f)(x - h)) / h;
		temp = y1;
		y1 = y2;
	} while (fabs(temp - y2) > eps);
	return y2;
}

//数值微分
//中心差商法
//x是要求导数的点，eps是精度要求，f是指向被积函数的指针
double CDFMiddle(double x, double eps, double (*f)(double))
{
	double h = 0.4;
	double y1 = ((*f)(x + h) - (*f)(x - h)) / (2 * h);
	double y2, temp;
	do {
		h /= 2;
		y2 = ((*f)(x + h) - (*f)(x - h)) / (2 * h);
		temp = y1;
		y1 = y2;
	} while (fabs(temp - y2) > eps);
	return y2;
}

//数值微分
//向前差商法
//x是要求导数的点，eps是精度要求，f是指向被积函数的指针
double CDFBefore(double x, double eps, double (*f)(double))
{
	double h = 0.4;
	double y1 = ((*f)(x + h) - (*f)(x)) /h;
	double y2, temp;
	do {
		h /= 2;
		y2 = ((*f)(x + h) - (*f)(x)) /h;
		temp = y1;
		y1 = y2;
	} while (fabs(temp - y2) > eps);
	return y2;
}

（三）插值型求导公式之拉格朗日插值微分法

1.概念

对于未知函数f(x)的函数表，利用拉格朗日方法建立插值函数L(x)的，用插值函数的导数近似f(x)的导数。

2.推理

（四）插值型求导公式之牛顿插值微分法

1.概念

和拉格朗日插值微分法一样，我们首先对曲线进行拟合，然后对曲线函数进行微分。前导内容可以查看上一篇数值计算的笔记（数值计算之函数逼近）

当使用牛顿多项式微分法进行求解的时候，其优点就是可以通过数据集而不必知道具体的函数表达式即可求解导数的较为精确的近似值，因为有的时候知道函数表达式并不是一件容易的事情，因此牛顿多项式在实际问题处理中具有较大的意义。

2.一些公式

来源于网络截图，其中P是根据牛顿插值法得到的多项式。根据最后的公式编程即可，代码在后面。

3. 代码（大部分来自于上一篇实验的改编)

//牛顿插值微分法，index表示插值点  
double Newton(int n, double x[], double y[], double index)
{
	double res = 0;
	double temp = 1;//temp用来记录每一项的分母 
	int i, j;
	for (i = 0; i < n; i++)
	{
		for (j = n ; j > i; j--)//计算差分 
		{
			temp = x[j] - x[j - i - 1];
			y[j] -= y[j - 1];
			y[j] /= temp;
		}
	}
	for (i = 2; i <=n ; i++)//系数*插值基函数 （index代入公式中的x） 
	{
		double leijia = 0;
		for (int k = 0; k <i; k++)//累加循环
		{
			double leicheng = 1;
			for (j = 0; j <i; j++)//累乘循环
			{

				if (j == k)
					continue;
				else
				{
					leicheng *= (index - x[j]);
				}
			}
			leijia += leicheng;
		}
		res += y[i]*leijia;//给答案加上！
	}
	res += y[1];//y[1]就是我们的a[1] 
	return res;
}

4.与拉格朗日插值微分法的一些关系

拉格朗日可以推导出更多的不同精度的不同阶导数的近似值表达式。

不过利用牛顿多项式的易于求导的特点进行一阶导数的求解，其精度极高，但也应当注意边缘发散的情况。

（五）运行结果及分析比较

使用的离散数据:

double x[7] = { 1,2,3,4,5,6,7 };

double y[7]={0.367879441,0.135335283,0.049787068,0.0183156,0.006737946999,0.00247875,0.0009118819655 };

1.用差商近似导数，从截断误差角度，步长越小越好近似程度越高；从舍入误差角度，因为h在分母，所以不宜过小。

2.三种差商中中心差商公式的精确度最高。

3.从几何上看，向前，向后，中心差商公式分别是以三点中的某两点间弦的斜率近似曲线中点斜率的。

4.两点前向差分（精度/截断误差为O(h)）、两点后向差分（精度为O(h)）以及两点中心差分算法（精度为O(h^2)）。一般来说，对称的中心差商与中点处的斜率更接近。

5.可以用一次、二次、三次插值多项式来得到导数的近似，近似结果也会随次数增高而改进。但次数增高到一定程度会出现龙格现象，然后结果就不准了。插值所用的点多一些会更接近实际值。

四、实验感悟

数值的积分和微分应用到的数学知识还是比较好理解的，主要是学过了微积分吧，另外上一次实验的拉格朗日和牛顿插值也为数值微分提供了新想法，稍加改编就好。主要还是要理解方法原理，照着公式编程并不是最难的事情。

程序和三三总有一个能跑

关注

7
点赞
踩
38

收藏

觉得还不错? 一键收藏
打赏
0
评论
数值计算之数值积分与微分

(1)编写用矩形法、梯形法和辛普森法求解定积分，并对三种算法的运行结果进行定性和定量的分析。 (2)请查阅文献整理求数值积分的其它方法，并至少编程实现其中的一种算法。结合（1）的结果对比分析几种算法的性能。 (3)请查阅文献整理求数值微分的其它方法，并至少编程实现其中的一种算法。一个函数在编译时被分配给一个入口地址，这个入口地址就称为函数的指针。可以定义一个指针变量指向函数，该指针称为指向函数的指针变量。1.定义p是指向函数的指针变量，它可以指向类型为整型且有两个整型参数的函数。p的类型用int(*)(i
复制链接

扫一扫