最小生成树&单源最短路径相关算法—Prim、Kruskal、Dijkstra——王道数据结构2025

LifeGPT

已于 2024-04-27 06:42:13 修改

阅读量716

点赞数 9

分类专栏：算法学习文章标签：算法图论

于 2024-04-27 06:34:16 首次发布

本文链接：https://blog.csdn.net/weixin_60519753/article/details/138235627

版权

算法学习专栏收录该内容

9 篇文章 1 订阅

订阅专栏

本文介绍了生成树和最小生成树的概念，探讨了如何在带权连通图中构建最小生成树，包括Prim算法和Kruskal算法的工作原理以及Dijkstra算法在单源最短路径中的应用。重点强调了最小生成树的性质和构建过程中避免形成环的原则。

摘要由CSDN通过智能技术生成

生成树&最小生成树概念

生成树概念

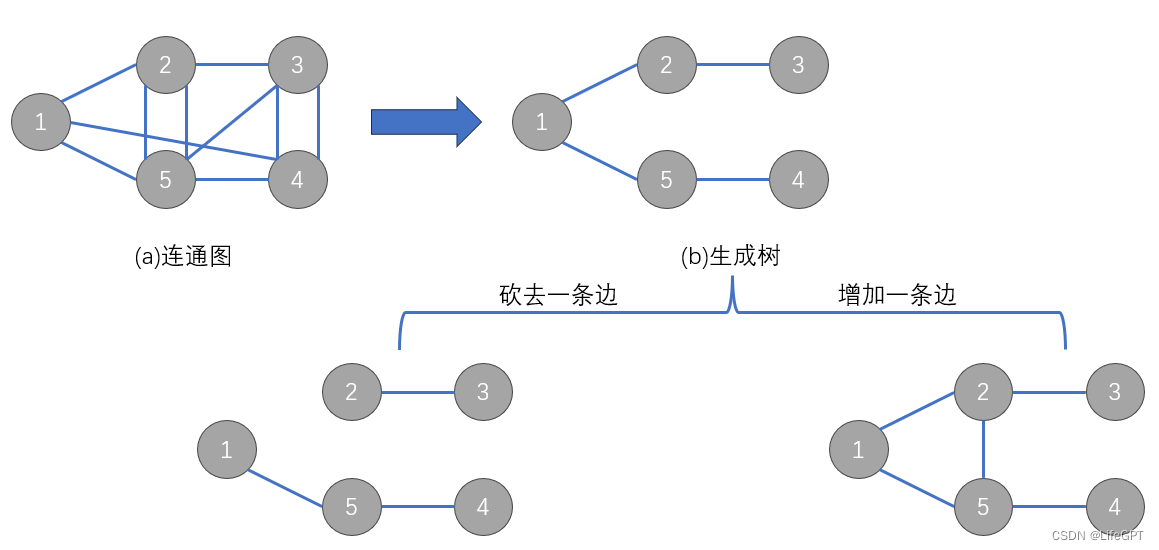
1、一个连通图的生成树包含原图的所有节点，并且只含尽可能少的边。

2、对于生成树：砍去一条边->非连通图；加一条边->形成一条回路。

最小生成树概念

1、一个带权连通无向图的可能形成的生成树中，权值和最小的那一颗生成树，即最小生成树；

2、为什么是可能形成的生成树中选择出最小生成树？

因为一个图可以生成多种类型的树，例如：

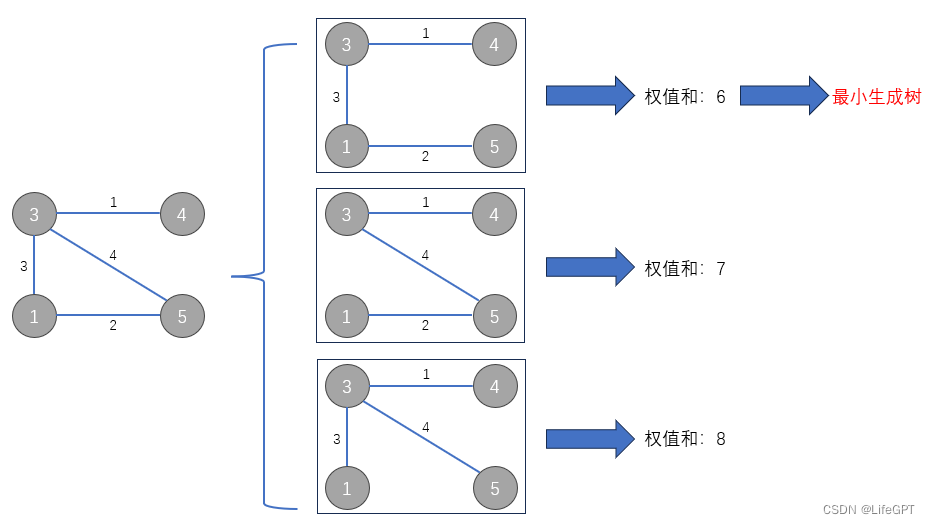
最小生成树性质：

1、存在权值相同->最小生成树不唯一；权值都不同->最小生成树唯一；例如(权值3重复)：

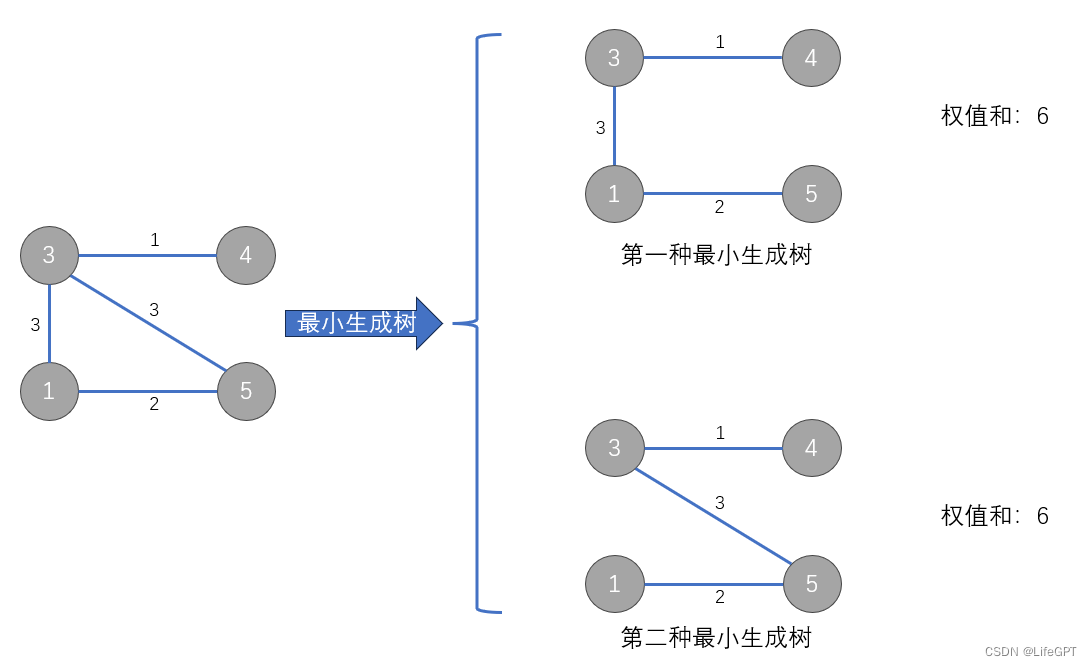
2、如上图，最小生成树即使不唯一，但每一颗的权值之和是唯一的，且都是最小的（之所以会发生最小生成树不唯一，是因为存在权值相同的边，此时可以选择保留一边，不同的选择会形成不同的树，但是这俩边的权值都是相同的，不论保留哪个都不影响最后的权值之和）

3、最小生成树的边数 E 等于顶点数 V - 1

构建最小生成树

基本性质

设带权连通无向图G = ( V , E ) ，其中：

G：代表带权连通无向图； V：G 中的顶点集合： E：G 中的边集合；

U 属于 V 的非空子集，u 是 U 中的元素，v 是 V - U中的元素；

若（u,v）是一条具有最小权值的边，则必存在一颗包含（u,v）的最小生成树；

看不懂？没事，我也看不懂：）......图解如下：

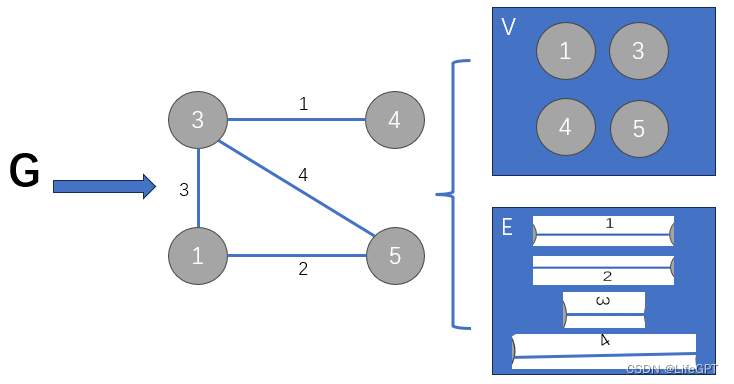
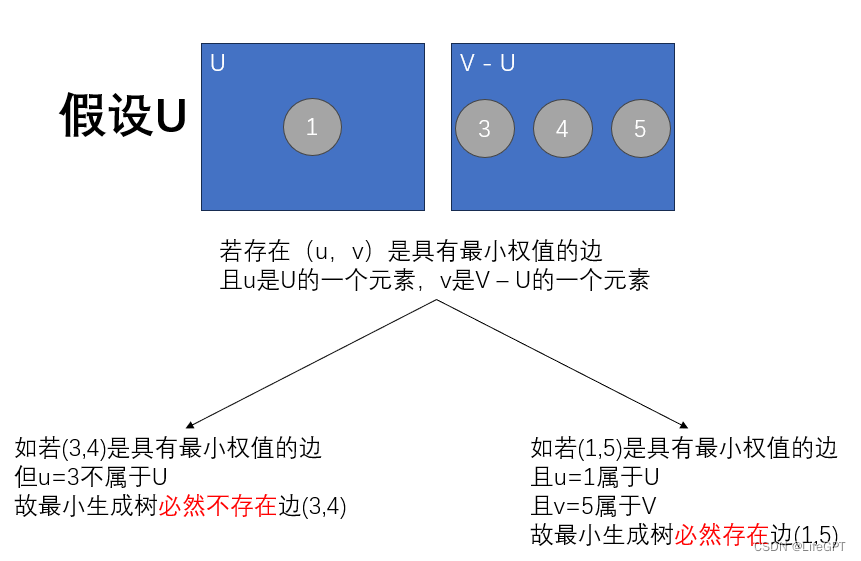
通用模版：

GENERIC_MST(G){
    T = NULL;
    while T 未形成一棵树；
        do 找到一条最小代价边(u,v)并且加入T后不会有回路产生；
            T = T 中加入边(u,v)；
}

Prim算法

Prim（普里姆）算法

假设原图为G={V , E} ，假设要求的最小生成树是 T = (U , $E_{t}$ )

其中的 $E_{t}$ 是最小生成树中边的集合，如 (u,v)

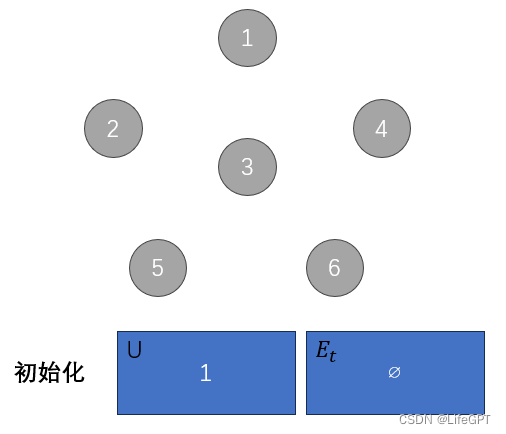
1、初始时，从图中任取一顶点加入树 T 中；此时的 T 中，U = {1}， $E_{t}$ = $\o$ ∅

2、（此步重复，直到U == V，即遍历完所有顶点）从G中选择一条( u , v )（注意，u是集合U的一个元素，v是集合V - U的一个元素，也就是说每次选的都是 u 的相连顶点 v 且不属于 U ），且（u，v）是最小权值的边，将该边，及顶点加入树 T ，即 v 并入 U 中，（u，v）并入 $E_{t}$ 中。

举例解释：

从图G中，可以知道，初始化后，U中只含有一个元素u，也就是 1 。所以接下来要寻找的最小权值边( u , v )就是当 u = 1 时的最小权值边( 1 , v )，那么竟然都说是最小权值边了，那在 1 的相连顶点中，就存在一个 v ，一定会使得（1 , v）是一个满足在 u = 1 的条件下的最小权值边。

从图中看出，v 可能的取值是 2、3、4，因为他们都是1的相连顶点，都可以构成( u , v )的格式，例如（1,2）、（1,3）、（1,4）,但我们要的是最小权值边，那么其中最小的当然就是（1,3），他的权值是1，而另外的两个是 6 和 5 ，都比 1 大，因此存顶点 3 到 U 中，存边到 T 中。

注意：第二次之后循环执行第2步时，U中的顶点数量肯定不止一个，需要全部列举，不理解可看下面图示过程。

图示过程如下：

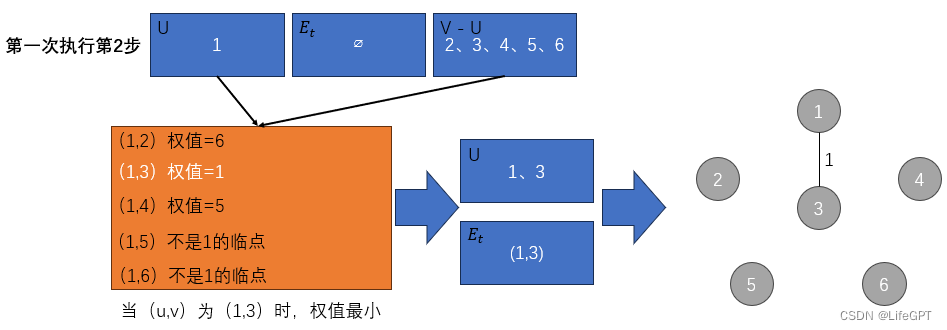
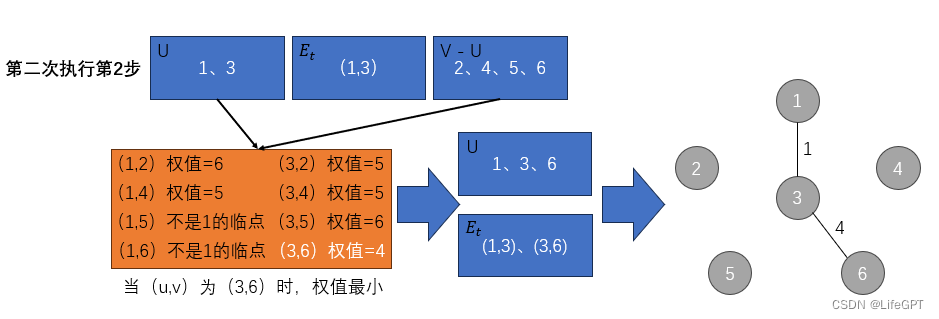
后面都是一样的步骤，重复执行第二步，不再赘述

总过程如下：

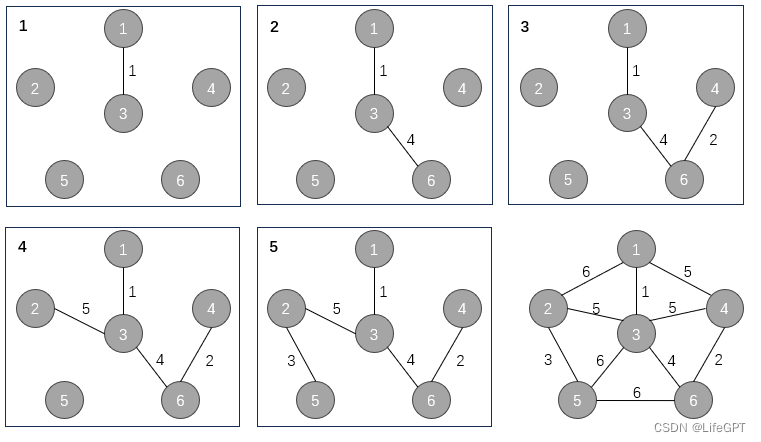
Kruskal算法

Kruskal（克鲁斯卡尔）算法

和Prim算法的区别：

Prim：顶点优先，优先寻找相邻顶点，再取所有边种的最小权值边

Kruskal：权值优先，依递增次序，优先寻找最小权值边

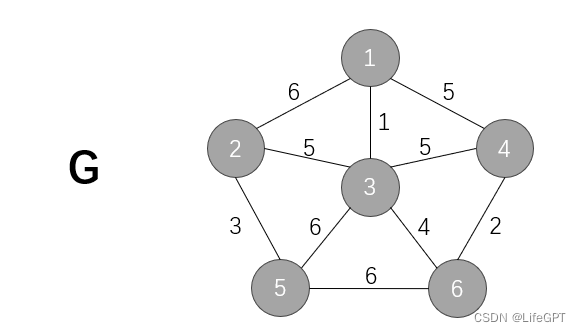
Kruskal从图例上可以比Prim更容易看出规律，故首先上图，先看看其规律是什么：

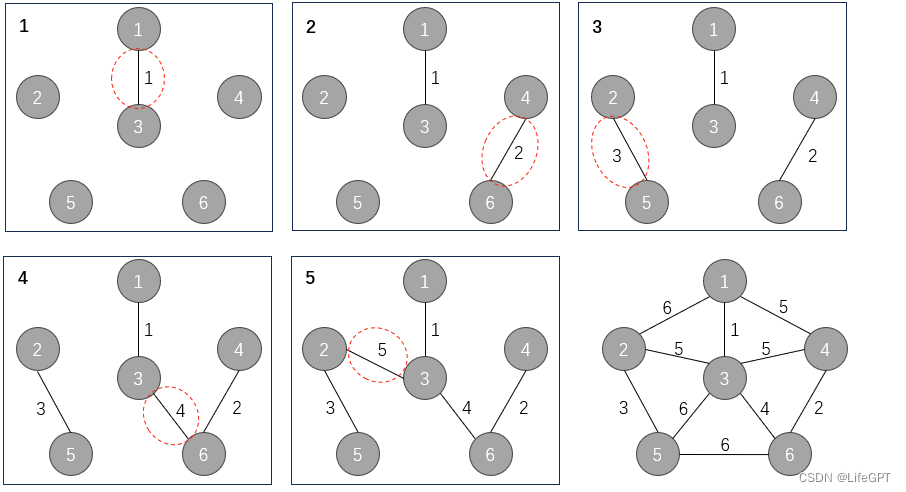可以看到，从最小的权值边 1 开始，逐渐到最后的 5

是否会好奇为什么 5 有那么多，为什么偏偏取这个，最后的 6 为什么又没了？

其实可以发现，如果取其他的 5 ，或者把最后的 6 取了，那么就会形成一个环了，这是不满足生成图要求边数尽可能少的条件的！！！

那在实际中该怎么处理这种情况？

首先在最开始状态，也就是在图例1之前，还不存在边，只有 6 个顶点，这也代表有 6 个连通分量，每个顶点代表一个。

进入图例1后，找到最小权值 1 的边，此时！！注意了，由于两个连通分量合在一起形成同一棵树了，所以这两个顶点成为了一个连通分量，即最开始原来的连通分量减一个。

有了上面连通分量的概念，下面会产生一些我学习的时候常见的问题：

针对问题：如果取其他的 5 会怎么样？

假设在图例4到图例5的过程中，选择了路径(3,4)，虽然其权值也是5，但是很明显产生了闭环346，不满足生成图的基本要求。那么这样，再返回看看图例4中，可以发现3和4是属于同一个连通分量内的，而3和2却不是，如果一个顶点连接了同一个连通分量内的其他点，那必然产生一个环，无法形成生成树，更别说最小生成树了。

针对问题：如果取最后的 6 会怎么样？

其实是一样的，最后连通 5 后，这就是个生成树了，而且是最小生成树，不存在连通分量了，还记得生成树的概念嘛？如果再加一条线，就必然产生环！！

针对问题：如何判断结束条件？

我们发现每次找到一个最小权值边，都会导致少一个连通分量，因此最后只剩下一整个树，也可以说只有一个连通分量，也就是它本身。所以只要设定一开始的时候，也就是没有任何边的时候的顶点个数（初始连通分量个数），假设为sumS，那么每次执行一次找到最小权值边，sumS就减一，最后只剩下一个的时候即可退出寻找最小权值边（可别把最后一个也减了）。

构建单源最短路径

对于无权图，可以用简单的广度优先搜索BFS找到单源最短路径，不用考虑权值大小。但是对于有权图，最短路径的含义是路径上的权值之和最小，可能包含更多的顶点但是权值之和却最小。这样情况就不同了。

Dijkstra算法

Dijkstra（迪杰斯特拉算法）中有几个比较重要的概念：

1、S集合，记录已求得的最短路径顶点，后续不会再改变

2、dist[ i ]数组，表示从 $v_{0}$ 开始到顶点 i 的最短路径长度，若 $v_{0}$ 到 $v_{i}$ 存在连接（有弧），那么dist[i]上存储的就是 $v_{0}$ 到 $v_{i}$ 的权值，否则为无穷∞

3、其实还有final[]和path[] 但是这里先不做考虑

算法基本步骤：

1、初始化，S集合加入图中随机一个初始顶点，dist[i] 存储从初始顶点到其他各个顶点的路径长度，如果用arcs[i][j]代表<i,j>有向边权值，那么dist[i]=arcs[初始顶点][i]，i = 1、2、3、.....、n-1；

2、从V - S的顶点集合中找出一个 $v_{j}$ ，使得dist[i] = Min{dist[i] | $v_{i}$ $\in$ V - S}， $v_{j}$ 即当前求得的一条从 $v_{0}$ 出发到最短路径的终点，再 j 加入到集合 S 中；

3、修改从 $v_{0}$ 出发到集合V - S上任意一个顶点 $v_{k}$ 的最短路径长度

若dist[j]+arcs[j][k]<disk[k] 那就更新dist[k] = dist[j]+arcs[j][k]，其中可以理解dist[j]+arcs[j][k]为当前到 j 的最短路径长度+ j 到 k 的长度；

4、重复第二步到第三步，操作 n - 1 次，直到所有顶点都在S中；

是不是很麻烦？下面细说一下

首先是初始化操作：

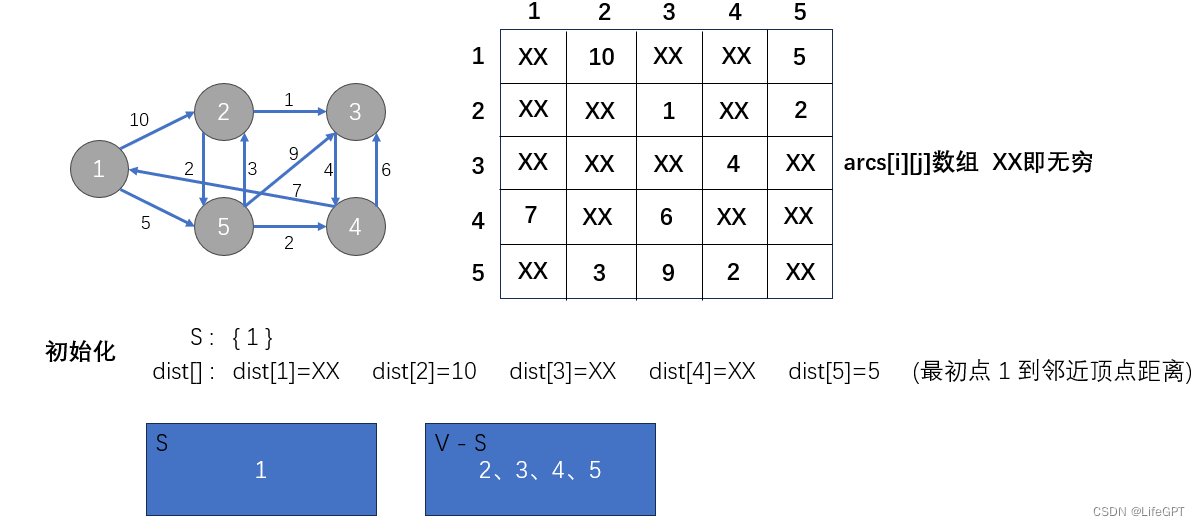
第二步操作：

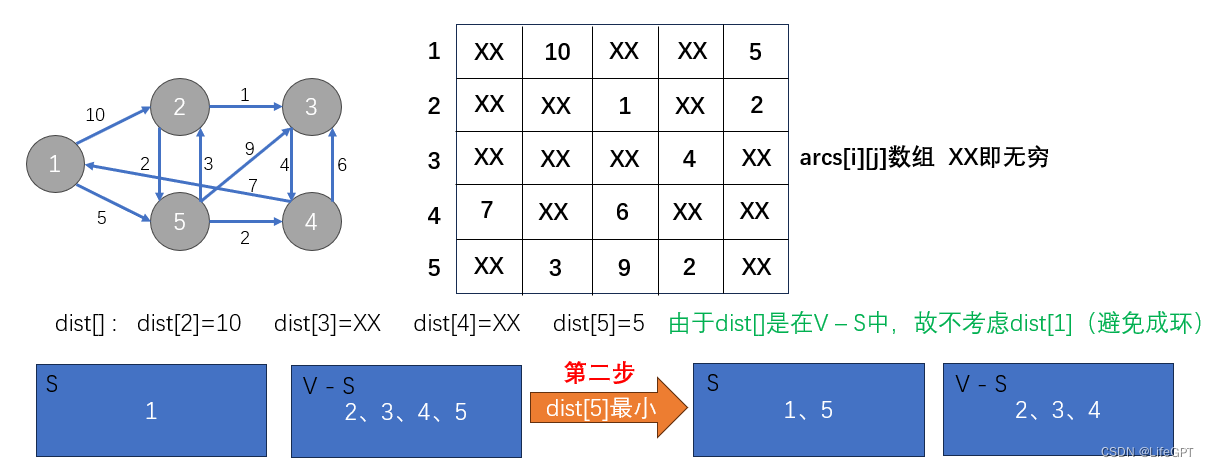
第三步操作（重难点）：

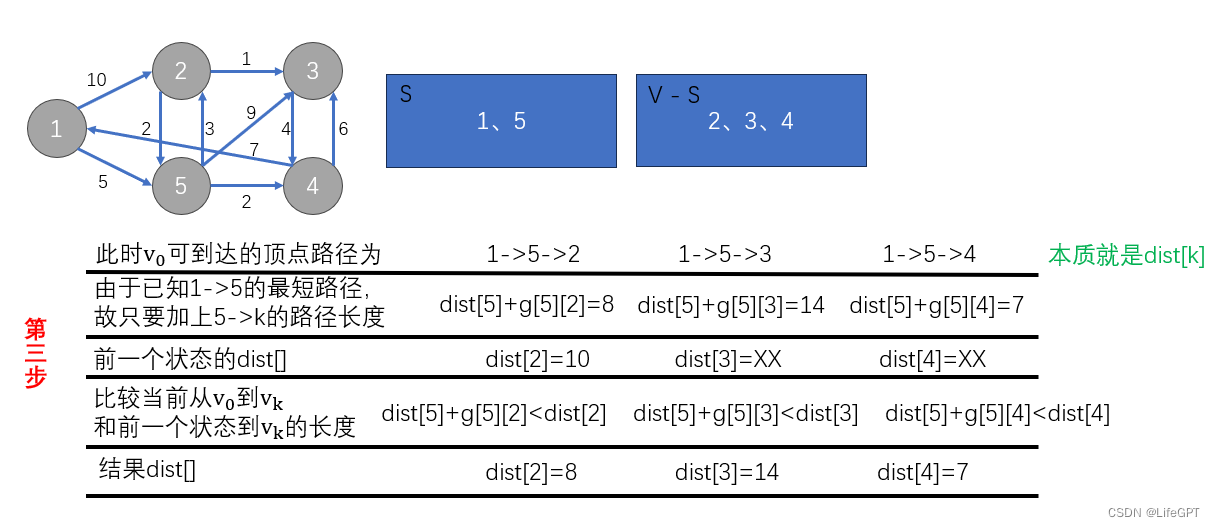
第三部分这里确实需要抽象的思考一下，否则很难转的过来，下面再阐述一下。

1、在第二步中，加入了顶点 5 ，这意味着，从1到5的最短路径已经确定了，永远不会再变了，而S集合的用处也就是保存已经确定的最短的路径的顶点；

2、那就只用考虑顶点 5 到其相邻的顶点长度即可，所以计算出从 5 到每一个到相邻顶点的长度；

3、算出每一个从1 -> 5 -> k（k = 2、3、4）的路径长度后，有没有发现，根据dist的概念，其实1 -> 5 -> k（k = 2、3、4）就是代表着dist[k]（k = 2、3、4），然后与先前的dist[2]、dist[3]、dist[4]即先前的从 $v_{0}$ 开始到这三个点的路径长度，如果当前算出某 k 的路径长度比之前的更短，那就修改dist[k] 为当前的最短路径长度即可。

4、得到最终结果的dist，又可以返回第二步进行循环了，一共n-1次操作