C语言——二维数组算法问题

 问题一：求矩阵各行元素之和

---

题目要求：

本题要求编写程序，求一个给定的m×n矩阵各行元素之和。

输入格式：
输入第一行给出两个正整数m和n（1≤m,n≤6）。
随后m行，每行给出n个整数，其间以空格分隔。
输出格式：
每行输出对应矩阵行元素之和。

输入样例：

3 2
6 3
1 -8
3 12 

输出样例：

9
-7
15 

---

解题思路：

1. 输入行列，然后依次输入矩阵
2. 遍历矩阵，每当遍历完一行一列，就做加法计算，并打印，然后把总和归零，继续进入下次循环 。

---

代码实现：

#include <stdio.h>
int main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	int i,j,arr[n][m];
	for(i = 0;i < n;i++)
	{
		for(j = 0; j < m;j++)
		{
			scanf("%d",&arr[i][j]);
		}
	}
	
	int sum = 0;		//用于记录各行的元素之和
	for(i = 0;i < n;i++)
	{
		for(j = 0;j < m;j++)
		{
			sum += arr[i][j];
		}
		
		printf("\n第%d行元素之和：\n",i+1); 
		printf("%d",sum);		//每行结束之后打印 
		sum = 0; 				//和归零，计算下一行 
	}
	
	return 0; 
}
 

---

运行结果：

---

问题二：求矩阵中的最大小值

---

题目要求：

 输入一个n×m的整数矩阵(n<=10,m<=10)，
然后输出其中的最大值、最小值，并输出这两个值所处行列（非下标）。

输入样例： 

3 4
65 77 21 88
23 99 18 54
19 82 73 99

输出样例：

max=99 row=2 col=2
min=18 row=2 col=3

---

解题思路：

1. 先输入矩阵，记录下一行一列元素（分别是最大最小值比较的初始值），用来标记后面找最大值最小值操作 ；
2. 遍历矩阵，分别找到最大最小，引入变量记录下标。
3. 输出行列位置，注意当时记录的是下标，输出的时候需要加一。

---

代码实现:

#include <stdio.h>
int main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	int arr[n][m],i,j;
	for(i = 0;i < n;i ++)
	{
		for(j = 0;j < m;j++)
		{
			scanf("%d",&arr[i][j]);
		}
	}
	
	int max,min,max_row,max_col,min_row,min_col;
	
	max = arr[0][0];		//开始找最大值操作，先赋初始值  
	for(i = 0;i < n;i++)
	{
		for(j = 0;j < m;j++)
		{
			if(arr[i][j] > max)		//遍历进行比较，直到找到最大值 
			{
				max = arr[i][j];
				max_row = i;			//记录行下标 
				max_col = j;			//记录列下表 
			}
		}
	}
	
	min = arr[0][0];		//找最小值操作 ，同上 
	for(i = 0;i < n;i++)
	{
		for(j =0 ;j < m;j++)		
		{
			if(arr[i][j] < min)
			{
				min = arr[i][j];
				min_row = i;
				min_col = j;
			}
		} 
	} 
	//输出时候行列记得下标加一 
	
	printf("max = %d row = %d col = %d\n",max,max_row+1,max_col+1);
	printf("min = %d row = %d col = %d",min,min_row+1,min_col+1); 
	
	return 0; 
}

---

运行结果：

---

问题三：矩阵运算

---

 题目要求：

给定一个n ×n的方阵，本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。

输入格式:
输入第一行给出正整数n（1<n≤10）；随后n行，每行给出n个整数，其间以空格分隔。

输出格式:
在一行中给出该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。

输入样例： 

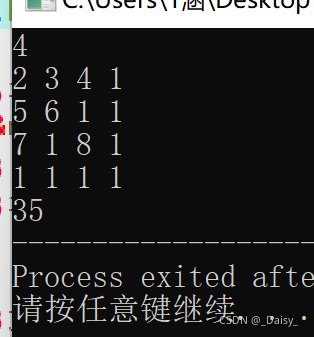
4
2 3 4 1
5 6 1 1
7 1 8 1
1 1 1 1

输出样例：

 35

---

解题思路：

        本题的切入点在于找到副对角线、最后一行、最后一列三者之间的关系 。

---

代码实现：

#include <stdio.h>
int main()
{
	int n,sum = 0;
	scanf("%d",&n);
	int i,j,arr[n][n];
	for(i = 0; i < n;i++)
	{
		for(j = 0;j < n;j++)
		{
			scanf("%d",&arr[i][j]);
			
			//找到最后一行，最后一列，副对角线的关系 ,不满足的就相加 
			if(i != n - 1 && j != n - 1 && j != n - 1 - i)
			{
				sum += arr[i][j];
			}
		}
	}
	
	printf("%d",sum);
	
	return 0;
	
}

---

运行结果：

---

问题四：判断上三角矩阵

---

题目要求：

本题要求编写程序，判断一个给定的方阵是否上三角矩阵。

提示：上三角矩阵指主对角线以下的元素都为0的矩阵；主对角线为从矩阵的左上角至右下角的连线。

输入格式：

输入第一行给出一个正整数T，为待测矩阵的个数。接下来给出T个矩阵的信息：每个矩阵信息的第一行给出一个不超过10的正整数n。随后n行，每行给出n个整数，其间以空格分隔。

输出格式：

每个矩阵的判断结果占一行。如果输入的矩阵是上三角矩阵，输出“YES”，否则输出“NO”。

输入样例：

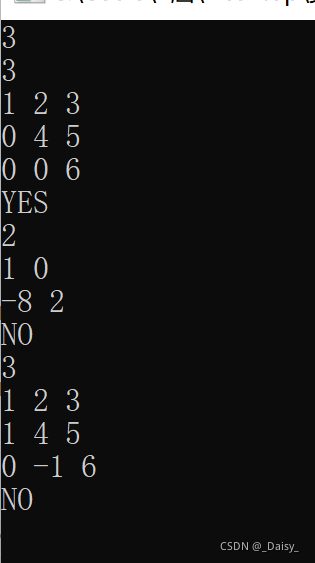
3
3
1 2 3
0 4 5
0 0 6
2
1 0
-8 2
3
1 2 3
1 4 5
0 -1 6

输出样例：

YES
NO
NO 

---

解题思路：

• 本题破解点在于三角矩阵的特点：行大于列 ，用此条则可以进行判断。
• 注意进出循环

---

代码实现：

#include <stdio.h>
int main()
{
	int num;		//规定判断几个 
	scanf("%d",num);
	
	int i,j,k,n;
	for(i = 0 ;i <= num;i++)
	{
		scanf("%d",&n);
		
		int arr[n][n];		
		int flag = 0;
		for(j = 0;j < n;j++)
		{
			for(k = 0;k < n;k++)
			{
				scanf("%d",&arr[j][k]);		//输入二维数组 
				if(j > k && arr[j][k] != 0)		//三角矩阵行大于列，且不是0
				{
					flag++;
				} 
			}
		}
		if(flag != 0)		//输入完毕一个完整的矩阵就进行判断 
		{
			printf("NO\n");
		}
		else
		{
			printf("YES\n");
		}
	}
	
	return 0; 
}

---

运行结果：

---

问题五：螺旋矩阵（基础版）

---

题目要求：

所谓“螺旋方阵”，是指对任意给定的N，将1到N×N的数字从左上角第1个格子开始，按顺时针螺旋方向顺序填入N×N的方阵里。本题要求构造这样的螺旋方阵。

输入格式：

输入在一行中给出一个正整数N（<10）。

输出格式：

输出N×N的螺旋方阵。每行N个数字，每个数字占3位，左对齐。

输入样例：

5

结尾无空行

输出样例：

1 2 3 4 5

16 17 18 19 6

15 24 25 20 7

14 23 22 21 8

13 12 11 10 9

结尾无空行

---

解决思路：

1.定义一个二维数组 ，要注意把外圈，起始，结尾分别做好标记，方便给方阵相应位置赋值；

2.从上下左右四个边界入手考虑，分别赋值，要思考上下左右各行各列行列之间的关系；

3.注意要控制外圈变量，也是循环终止的条件；

4.注意赋值以后，边界的缩进问题；

5.注意奇偶问题，如果输入的n为奇数，要考虑单独给方阵最中间的那个位置单独赋值；

6.最后注意格式问题，每个数字占三位，左对齐。

---

代码实现：

#include <stdio.h>

int main()
{
	int row,line,n;
	int  value = 1;
	
	scanf("%d",&n);
	int a[n][n] = {0};
	int out = n,end = n,start = 0;	//分别表示外圈循环标记，起始和末尾
	
	while(out > 1)
	{
		for(line = start ; line < end ; line++)		//上 
		{
			a[start][line] = value++;
		}
		for(row = start + 1 ; row < end ; row++) 	//右
		{
			a[row][end - 1] = value++;
		} 
		for(line = end - 2 ; line >= start ; line--)	//下
		{
			a[end-1][line] = value++;
		}
		for(row = end - 2 ; row > start ; row--)		//左 
		{
			a[row][start] = value++;
		} 
		
		out -= 2 ;			//控制外圈变量
	
		//边界缩进一格
		start += 1;			
		end -= 1; 
	 } 
	 
	 //注意 n为奇数，需要给矩阵中间赋值
	if(n % 2 != 0)
	{
		a[start][end - 1] = value;
	} 
	for(row = 0 ; row < n ; row++)
	{
		for(line = 0 ; line < n ; line++)
		{
			printf("%-3d",a[row][line]);	//要求数字占三位且左对齐
		}
			printf("\n");
	}
	
	return 0;
	
} 

---

运行结果：