目录
前言
hi~( ̄▽ ̄)/
欢迎大家能够点进我的文章٩(๑❛ᴗ❛๑)۶,这一篇,只是我对排序用c语言实现的一些粗糙的想法,讲的就是数据结构里面的选择排序,交换排序,插入排序啦~ヾ(✿゚▽゚)ノ,这里我会尽量用思路加图解的方式将每一个排序大致弄懂的啦~
还请大家多多支持或者给我指出错误,我们能够一起共同学习呀!φ(>ω<*)
ps:下面的排序均以升序为基准!
一.选择排序:
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。(百度百科)
综上,实现内容就是基于选择。下面我们实现基本利用遍历来选择的排序和利用堆的结构实现选择的堆排序。
准备好了吗 ̄ω ̄=,开始吧!
1.选择排序
(只使用遍历实现的基础排序)
思想:
每一次在未排好的数组里选择一个最大的和最小的,最大的放在未排好的数组的最左边,最小的放在未排好的数组的最右边,然后缩小范围,重复上述步骤,知道范围缩小为0或者1结束。
让我们利用图解更直观的了解一下吧~ヾ(◍°∇°◍)ノ゙
图解:
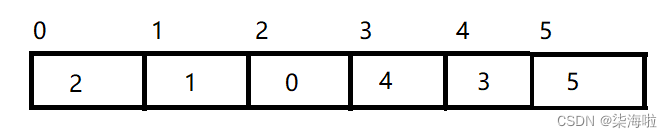
(下面的单词均是代表下标,方便数组内进行交换)
1.首先在0~end(5)这个范围里进行选择:(利用left和right来确定范围,此时一个为0一个为5)
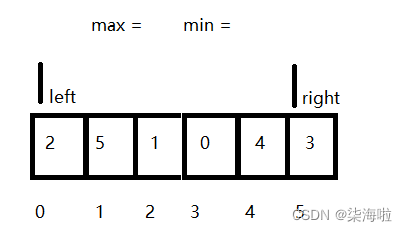
2. 在这个范围里面,我们依次对比(先将max和min初始的赋予一个值,依次和遍历的数字对比即可),便就可以找到max = 5, min = 0
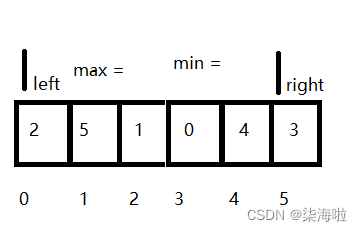
3.然后,将最大的max 和right进行交换,min和left进行交换:
先交换max和right:
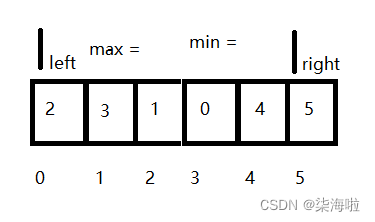
再交换min和left:
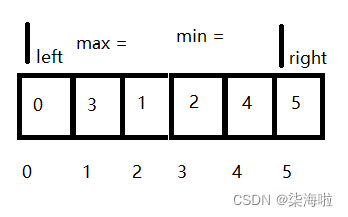
但是,经过事后分析,这里也一个有意思的地方,对后面的代码实现有作用:
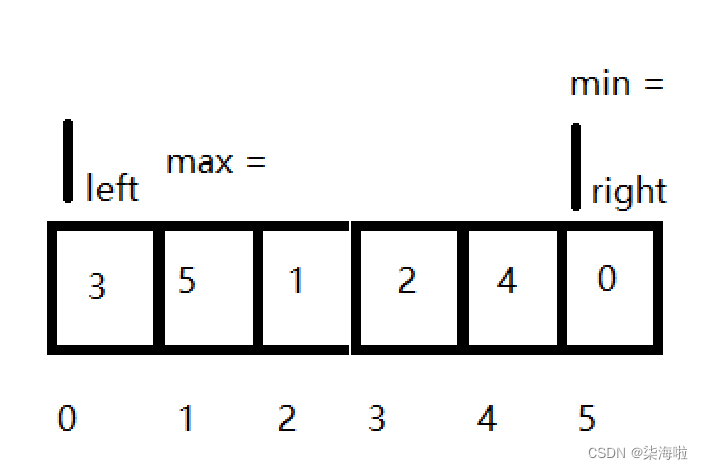
这种情况下交换后会不会出什么问题呢?嘿嘿(o゚▽゚)o ,我们后续会揭开哦~此时可以自己想一想ヾ(●´∀`●)
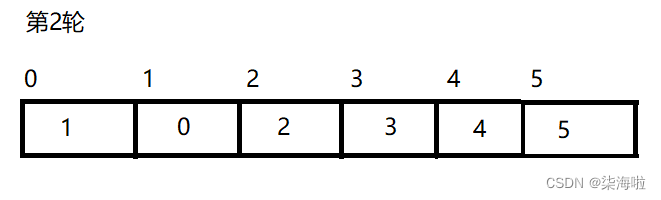
4.交换完毕后,left++,right--缩小范围,对新的范围进行新的一轮选择:
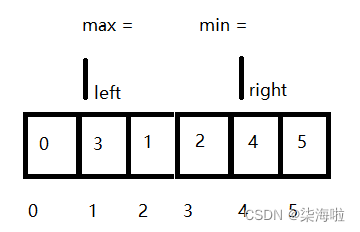

找到后交换即可,然后进一步缩小:
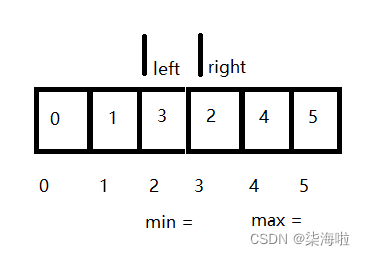
找最大最小:
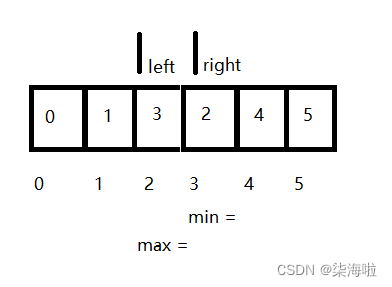
然后交换max和right,然后再交换left和min,但是此时就会出现我们上面提到的那个问题,这样导致的结果就是:
先交换max和right: 然后交换min和left:
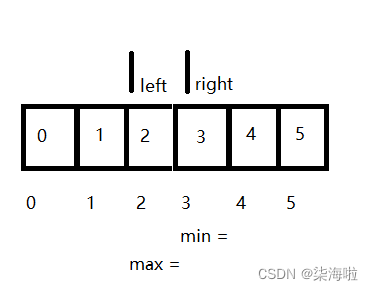

然后就发现了什么?竟然复原了?!这就是再第一次交换中,把原本min指向的地方给修改成3了的原因,所以,再连续两次交换的时候,要注意上一次交换是不是把原位置给换掉了,所以我们只需要再交换了大数后判断min是否等于right,等于的话给max就到了交换后min所指向的位置啦,得到这个正确的排序:
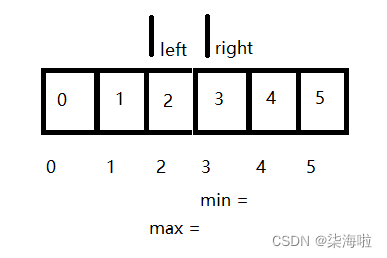
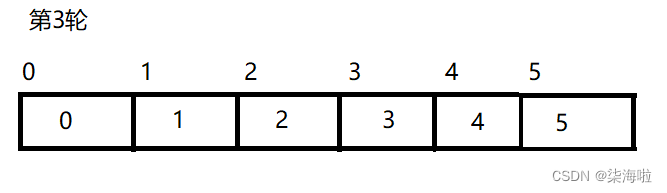
然后left++,right--
5.此时发现left>right了(当然数组个数存在偶数奇数的情况,我们图解的例子就是一个偶数,所以执行第四步后,left=3,right=2,如果是奇数,此时会两者相等,所以为了统一奇偶数,就可以用right>left这个条件来判断哦~) 范围为0,跳出循环,排序结束。
实现:
1.我们利用left和right来控制范围,并且也作为每次大数往最右放,小数往最左边放的基准。
循环条件也可以通过上述的图解来了解到,当left>right就跳出循环,我们这个排序,传来得参数自然就是数组a和整体个数n了,一开始的初始范围就是left= 0,right = n - 1。每次完后就left--,right++即可。
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while(left < right)
{
right--;
left++;
}
}2.然后就要实现里面的核心代码选择了:
根据图解我们了解到,每次我们是在一个范围内进行选择最大的最小的,涉及到选择,那么自然就要比较,那么一开始拿什么比较呢?只需要给最小的和最大的一个初值即可,这个初值可以是这个范围里的任意值,我们这里就给一开始的left下标啦(。◕ˇ∀ˇ◕)
int mini = left, maxi = left;然后进行循环,并且执行if语句,如果比原本的大或者小就更新min和max下标即可。循环只需要在这个范围里面就好。
for(int i = left; i <= right; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}然后交换,这里为了方便可以写一个交换函数,就穿指针进行保证实参得到修改即可。Swap();
等for循环遍历完后,然后将max和right进行交换,交换后判断min和right是否相等,相等的话把max赋给min,因为如果相等,那么第一次交换时已经将min原本指向的值换到max指向的位置了。然后进行第二次交换即可。
Swap(&a[right], &a[maxi]);
if (mini == right)
{
mini = maxi;
}
Swap(&a[left], &a[mini]);3.综上,完整代码是:
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while(left < right)
{
int mini = left, maxi = left;
for(int i = left; i <= right; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[right], &a[maxi]);
if (mini == right)
{
mini = maxi;
}
Swap(&a[left], &a[mini]);
right--;
left++;
}
}
*2.堆排
(使用堆结构进行选择排序)
思想:
前提:要充分了解数据机构里面的堆结构哦~这里可以简单的叙述一下堆结构(充分了解的可以跳过这个{}中的内容哦!|ू・ω・` ))、
{
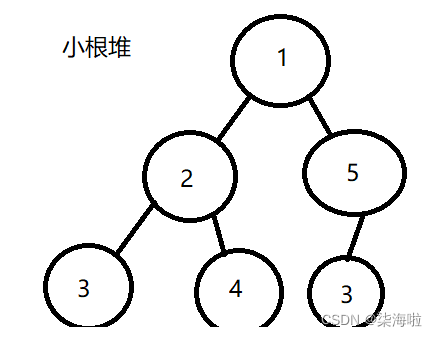
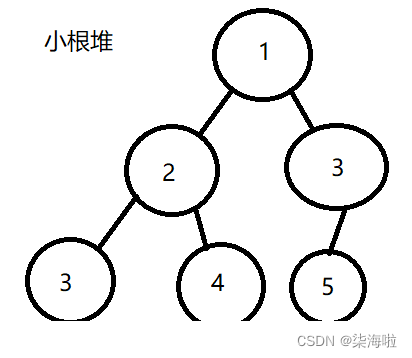
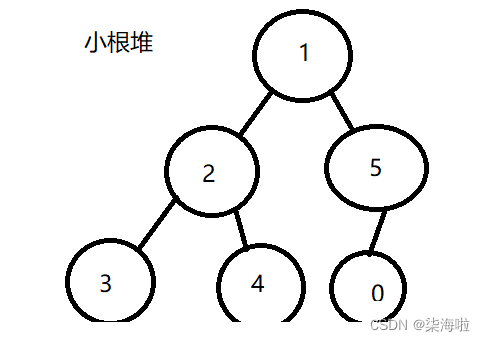
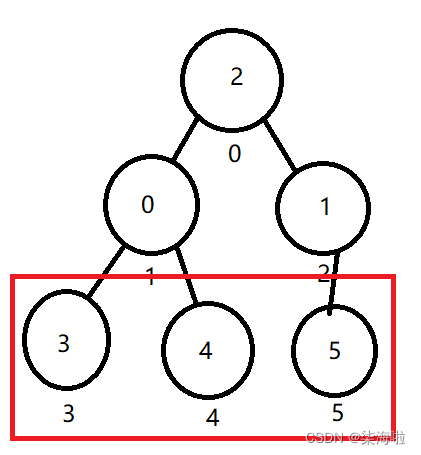
所谓堆,就是一个完全二叉树的结构,只不过,我们可以利用这个结构建立一个全新的数据之间的关系,堆。堆分两种,一种是小根堆,一种是大根堆。小根堆就是父节点一定一定比子节点小哦,子节点直接不区分大小;同理,大根堆就是父节点一定一定比子节点大,子节点直接不区分大小。如下图分别表示了小根堆和大根堆:(还是利用上面的数组数据)
当然,只要保证父节点和子节点之间的关系就好,不用管相邻之间的关系。
}
那么,我们要用堆结构进行排序,即利用小根堆和大根堆的性质和堆结构中的重要代码:向上调整和向下调整进行的。(实现堆结构也是利用的这两个调整)
现在重点讲一下向上和向下调整的这个思想过程,只有了解这个过程之后,才能理解堆排的实现过程:
1.向上调整:以小根堆为例子
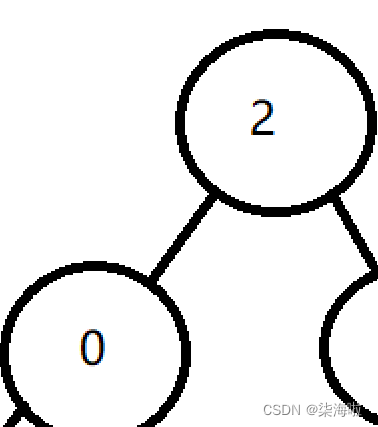
我们实现堆的时候,插入就是用的小根堆,堆得实际结构就是一个数组(物理上是连续的内存),所以,每次插入就是插入的最后一个元素,但是通过完全二叉树的性质(详情请见我的上一篇博客哦~(*^▽^*)),我们可以计算出此处的父节点位置对应的值,和它进行比较,因为是小根堆,所以如果比父节点小就进行交换,否则不换。比如:
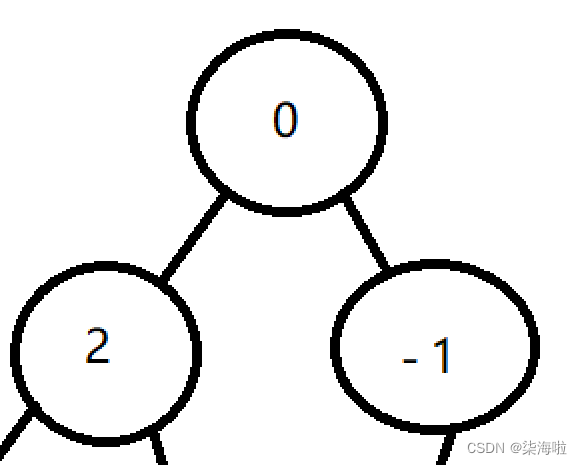
先插入2,然后插入0和其比较,发现比父节点小,进行交换。
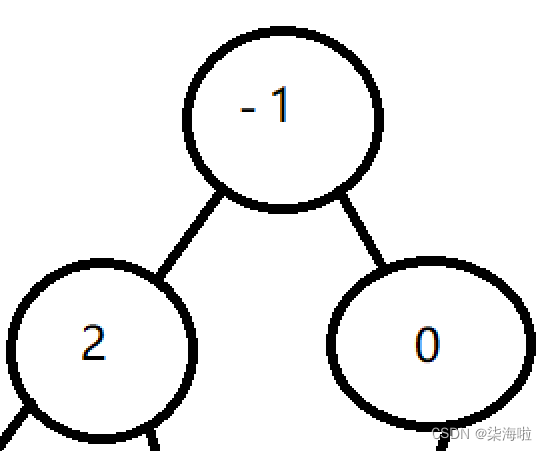
然后插入-1,重复上述步骤.......
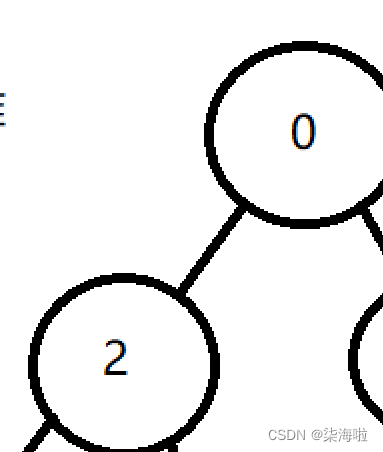
这样就可以实现向上调整啦!每一次插入这样做是不是就成为了一个堆结构了呢~|ू・ω・` )
我们可以顺手的算一下时间复杂度:
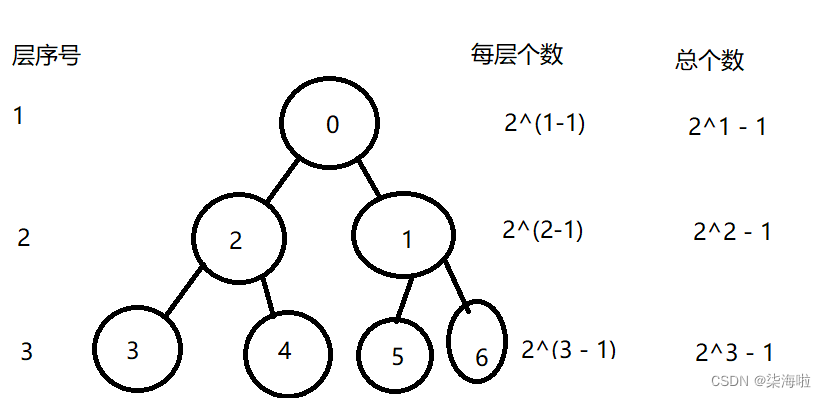
首先参考一下例图:
假如插入n个数,那么按照最坏情况,每一次插入就要交换,假设插入到了k层,根据完全二叉树的相关性质:(每层个数2^(k - 1) 总个数2^k - 1(k表示第几层))我们可以通过每一层的个数:2^(k-1),然后这一层要往上交换k - 1次,依次以层来计算,那么总共的次数s(k)就可以表示为:
s(k) = 2^1 *1 + 2^2 * 2 + ..... 2^(k - 1) * (k - 1);
这是一个差比数列,差比数列要求前k项和的话,只需要乘以一个公比,然后和原来的式子相减即可:
(1) s(k) = 2^1 *1 + 2^2 * 2 + ..... + 2^(k - 2) * (k - 2) + 2^(k - 1) * (k - 1);
(2) 2s(k) = 2^2 *1 + 2^3 * 2 + ..... +2^(k - 1) * (k - 2) + 2^(k) *(k - 1);
(1)-(2):
-s(k) = 2^1 + 2^2 + ..... + 2^(k - 1) - 2^k *(k - 1) ;
前面k-1项又是等比数列,所以:
-s(k) = 2*(1- 2 ^(k - 1))/(1 - 2) -2 ^k*(k - 1);
整理得到: s(k) = 2 - 2^k + 2 ^k *(k - 1) = 2^k *( k - 2) + 2;
又由总个数可以得到:n <= 2^k - 1,所以2^k >= n + 1
所以,k就近似的约等于log 2 n,这里简写为logn。
那么s(k)也就可以近似的表达为:n*(logn - 2) + 2;保留影响最大的部分,该算法的时间复杂度就是:O(n*logn)
(以上推理存在问题的话还请大佬指正!|*´Å`)ノ )
2.向下调整:也是以小根堆的例子
我们实现堆的时候,删除元素,检查结构就是使用的向下调整。向下调整适用于除开目标节点外其余节点均是堆的结构。基于此,我们在堆结构里面删除元素就是首先最后一个和第一个元素交换,然后删掉,随后从头开始进行向下调整即可。和向上调整类似,通过性质计算出该父节点的两个子节点,然后两个子节点进行比较谁更小,然后最小的那个和父节点进行比较,比父节点小就交换,依次往下......
比如:
首先,此时这个结构就是除了头节点外,其余满足小根堆的这个结构哦~
然后通过计算,比较两个子节点(2, 1)谁更小,显然1更小,然后和父节点交换:
然后,以交换后的子节点为父节点,重复上述步骤,得到:
* 注意,你此时可能会存在一个疑惑,这只是一次交换,那么万一交换后比上一个父节点小呢?o(´^`)o
这种情况就是下面这样类似的了:
但是难道没有发现吗?这本身再改之前就不是堆的结构了,这也就是为什么我们要求除开被改节点一下满足堆的结构呢?
同样的,我们也在这里算一下时间复杂度:
同样的,以上面的例图为例:
也是插入了n个数,从头开始往下检查:如果存在交换,就只是和下一层交换即可,所以这里也设插入到了k层,s(k)表示检查的总最坏次数:
s(k) = 2^0 + 2^1 + 2^ 2 +....... 2^(k - 1);
直接就是一个等比数列求和,得到:s(k) = 1*(1 - 2^k)/(1- 2) = 2^k - 1;
又n <= 2^k - 1;所以,s(k) = n 啦!
所以,该算法的时间复杂度就是O(N);
综上,向下调整显然比向上调整更具备优势。我们可以同时利用向下调整来建堆,然后在用向下调整来进行选择排序。
那么介绍一下向下调整建堆和选择的大致过程:
1.向下调整建堆
因为向下调整已经明确好了,从检查的那一方往下走,下面必须满足堆(完全二叉树)的结构,那么一开始杂乱无章的数组里面,要从头开始的话就完全不满足哦,ψ(*`ー´)ψ,所以,我们反其道而行之,从最后一个开始向下调整不就完了嘛。那么,这里我们是建立大堆还是小堆呢?
2.建立什么堆呢
我们这里使用的是升序,升序,我们就要每次选择最小的到最前面去,最大的,到最后面去。既然是向下调整来进行选择,那么应该用于交换后,让上面部分的堆恢复堆的结构(类似于删除元素),恢复的目的自然是头结点的最大和最小,那么肯定是和最后一个元素交换。最大的到最后面去,所以升序就应该建立大根堆啦~
图解:
诶嘿嘿嘿,图解来咯~|ू・ω・` )
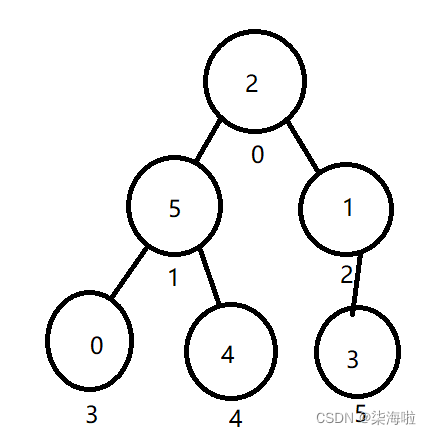
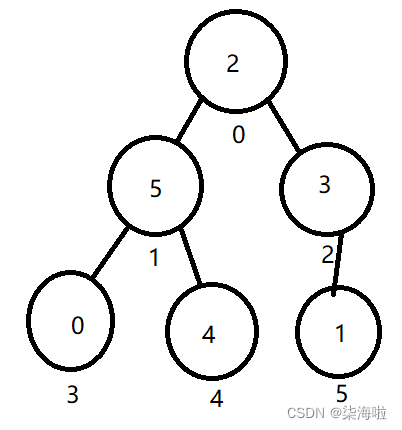
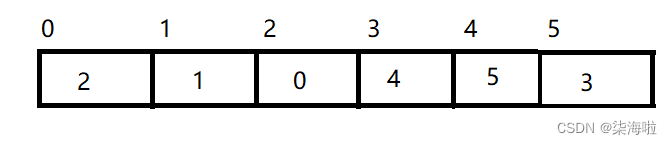
同样的,我们以上面的数组为例,这是一个物理结构,按照这个物理结构存放的数据来排成一个二叉树的话,应该是下面这张图的样子:
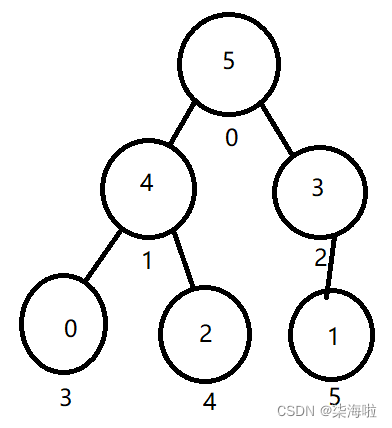
然后,我们开始1.向下调整来建堆:
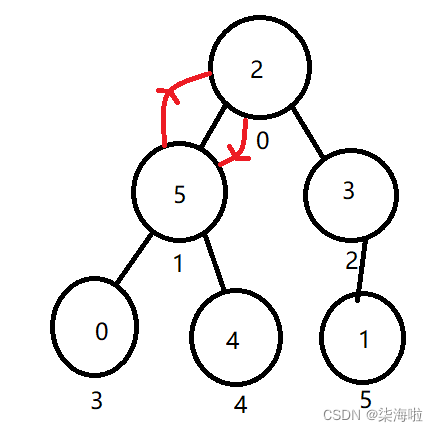
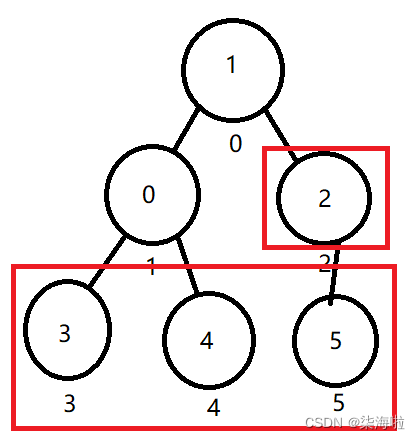
从思想里面我们知道,从后往前建堆,好的,利用遍历,将下标5,4,3这三个遍历之后均没有任何问题,一直到了2这个下标,因为是要建立大根堆,所以,父节点必须要比子节点大,1是小于3也就是小于子节点,子节点只有它一个,所以子节点无需比较,1和3交换即可。
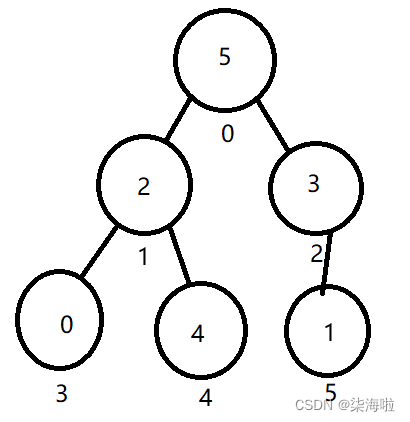
然后遍历到下标为1的节点,首先有两个字节点,比较看谁大,是4比较大一点,然而父节点5是比4要大的,所以不做改动。
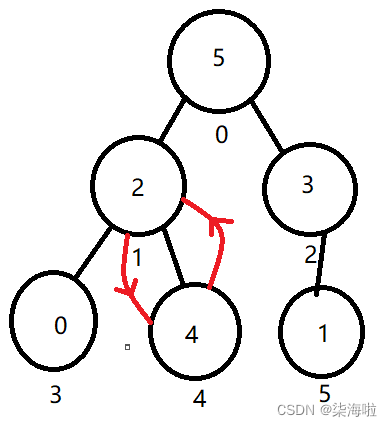
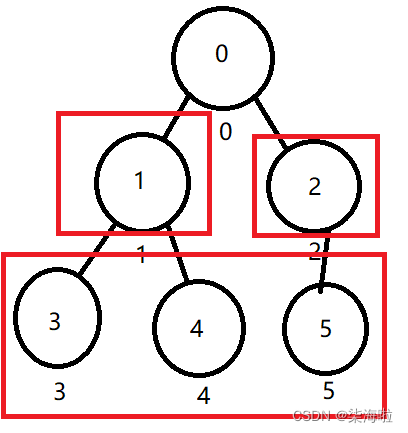
然后遍历到下标为0的节点(头节点),首先5和3比较,5比较大,5又是大于2的,所以,5和2交换,然后2又和下标为1的节点的子节点进行比较,比4小,所以和4交换。
然后遍历完成,观察最后一张图,是不是大根堆我们就建立完成了呢!(✪ω✪)
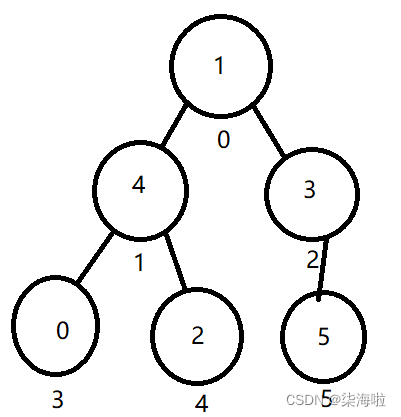
接着,我们利用2.向下调整来选择进行排序:
首先,0节点位置和5节点位置交换数据,然后从头开始(除开尾巴)进行向下检查:
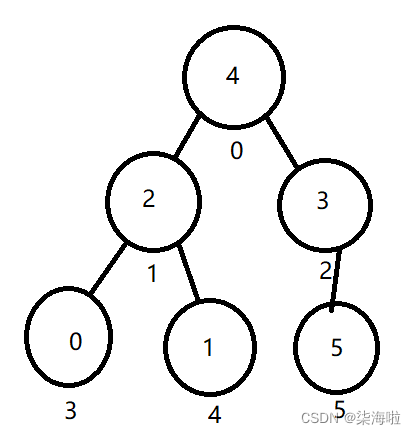
然后此时我们发现,堆的结构又为我们选好了第二个大的结构,重复上述步骤,调整时跳过后面两个:
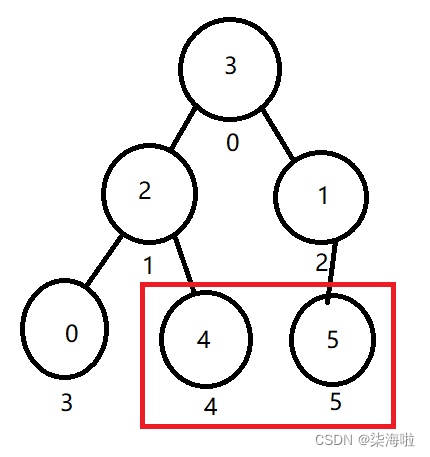
继续重复上述动作直到只剩一个头节点结束:
此时,就会惊喜的发现,此时数组里面的数是不是就是升序啦!我滴人物完成啦!哈哈哈哈~
实现:
终于,万水千山终于来到了你的面前~(╥╯^╰╥)
首先呢,我们实现向下调整这一核心代码:
1.向下调整
首先来看看形参,我们肯定是要传过来一个数组的,还有一个数组的长度,以及传过来的节点,这个节点此时代码是围绕着这个向下进行检查的,所以这个节点肯定是父节点。
void AdjustDwon(int* a, int n, int parent)然后,我们知道,我们要找到此时的父节点的两个子节点,然后两个子节点进行比较,谁大谁小,谁大就和父节点进行比较(建立大堆),我们可以建立两个来储存子节点下标的变量,但是可以更简单一些,初始将子节点赋给左节点,然后左右相比较(右节点=左节点+1),如果左节点更大,左节点加一就好了。此时的框架可以如此搭建:
int child = parent * 2 + 1;
if (a[child + 1] > a[child])
{
child++;
}然后这里这一部分肯定是要放在循环里面的,我们可以先不考虑循环条件,先将逻辑分析清楚:
选择完之后,然后大的子节点和父节点比较,如果子节点大,就进行交换,交换完之后,为了进行下一步的交换,将此时的交换后的子节点看作父节点,然后在计算子节点;如果没有进行交换,那就说明此时已经是一个大根堆了(进入是满足除开父节点一下均是堆结构),直接跳出循环:
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;然后,我们就要控制住循环条件了,注意看,变化的是父节点和子节点,如果以父节点为判断逻辑,那么应该是parent<n的,但是在这种条件下,随便假设一下如果parent = n - 1,此时的依然能够进入循环,而计算出来的子节点早就已经越界了,所以,我们应该以计算的子节点为判断逻辑,即child < n即可
while (child < n)但是,注意,涉及到数组下标,就要考虑到越界问题。如果此时只是传一个头节点(数组里只要一个值),计算child = 1,那么可以不用进入循环,但是如果是只有两个节点呢?child = 1,1是小于2的,但是在一开始判断左右谁大的时候child + 1 = 2已经越界了哦~所以,我们应该对左右比较的判断逻辑上进行修改,防止任何一条漏网之鱼!
if (child + 1 < n && a[child + 1] > a[child])综上,向下调整的整个代码是:
void AdjustDwon(int* a, int n, int parent)
{
assert(a);
int child = parent * 2 + 1;
while (child < n)
{
//极端情况,只有两个元素:child + 1 = n不存在此下标
if (child + 1 < n && a[child + 1] > a[child])
{
child++;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
(Swap是交换哦~自己写的)
2.利用向下调整进行选择排序:
首先,这里就是实现排序的地方啦,也是向外提供和展示的地方,所以,堆排可以以heapsort来命名哦~传入的是数组和数组大小:
void HeapSort(int* a, int n)首先,依据数组本身,我们对它进行建堆。从最后一个元素开始,到头元素为止,进行向下调整即可:
for (int i = n - 1; i >= 0; i--)
{
AdjustDwon(a, n, i);
}然后,堆就建立好啦!接下来就是利用大根堆最大的在顶元素的性质,头尾交换,每次调整用向下调整即可。
for (int i = 0; i < n; i++)
{
Swap(&a[0], &a[n - 1 - i]);
AdjustDwon(a, n - 1 - i, 0);
}综上,堆排的整个代码是:
//向下检查:
void AdjustDwon(int* a, int n, int parent)
{
assert(a);
int child = parent * 2 + 1;
while (child < n)
{
//极端情况,只有两个元素:child + 1 = n不存在此下标
if (child + 1 < n && a[child + 1] > a[child])
{
child++;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
//升序建立大堆
void HeapSort(int* a, int n)
{
assert(a);
//通过向下检查建立一个大根堆:那么建立的时候,是要求下方是完全二叉树结构(堆)所以要建立,就是从后面开始
for (int i = n - 1; i >= 0; i--)
{
AdjustDwon(a, n, i);
}
for (int i = 0; i < n; i++)
{
//首先头和尾巴交换(最大的放在最后面)
Swap(&a[0], &a[n - 1 - i]);
//然后从头开始向下检查,除开最后一个元素即可
AdjustDwon(a, n - 1 - i, 0);
}
}二、交换排序
交换排序来啦~(*´゚∀゚`)ノ 这个自然就是第二梯队了。交换排序实际上就是涉及两个数比较,不过就交换即可。有冒泡排序和快速排序哦~
1.冒泡排序:
思想:
冒泡排序相信早就已经是大家的老朋友啦~它是通过每一轮把最大的传到最右边去,只需要让没有排序好的部分两两比较,大的往左交换即可。然后遍历完后,排序就完成啦~(*/ω\*),果然还是老朋友更关系我们呀~
图解:
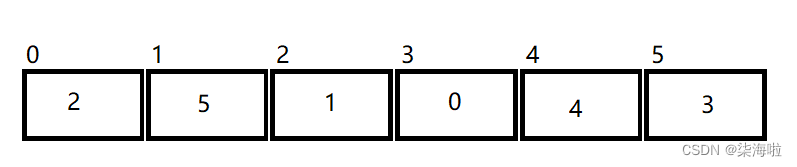
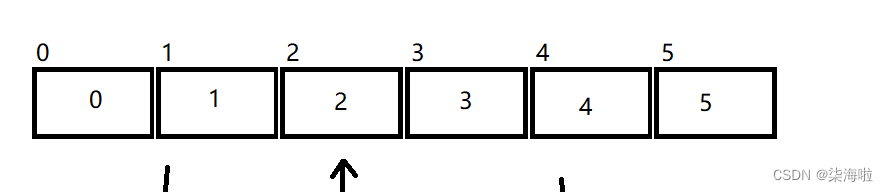
仍然以这一段数组保持的数据为例:2 5 1 0 4 3
首先,进行第一轮交换:
0号和1号进行比较,1号比0号大,无需交换;1号与2号比较,1号大,需要交换。
然后2号和3号进行比较,2号大,交换。
3号和4号比较,3号大,交换:
4号和5号比较,4号大,交换:
第一轮结束,然后继续上述步骤,只不过这次最后一个下标就是5-1=4了,然后到3,到2,直到1结束;
此时我们发现了一个有趣的事情,此时在第三轮就变成升序了,但是还剩下两轮,为了提升效率,在下一轮检查时,检查完一遍发现未发生交换即可break跳出整个循环,就可以提升效率拉!
实现:
首先,我们可以把大致逻辑弄好哦,先不管进行第几轮的外层实现,那么第一轮的时候,左右两两比较,然后传递到最后即j + 1 = n - 1即可,所以,实现的大致逻辑是:
for (int j = 0; j < n - 1; j++)
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
temp = 0;
}
}然后这就是第一轮,接下来我们控制轮数,就要从j<n-1入手,控制的变量就为i,第一次i = 1,第二次为2,最后一轮就是n-1了,所以顺利成章,外层遍历代码是:
for (int i = 1; i < n; i++)之前在图解部分讲过,若发现遍历一遍(未排序的部分,第二层遍历)发现未发生交换,就跳出整个循环嘛,所以我们可以定义一个flag来确定是否交换的状态,在交换的代码里面随便赋值,然后再第二个for循环的下面进行if语句控制即可:
for(...
{
int temp = 1;
for(...
{
if(..
{
...
temp = 0;
}
}
if(temp)
break;
}
综上,实现冒泡排序的代码是:
//冒泡排序:
//思想,每次相邻两个元素比较,右边小的话就交换,把这一趟的最大数传到这一趟的最右边去
void BubbleSort(int* a, int n)
{
assert(a);
for (int i = 1; i < n; i++)
{
int temp = 1;
for (int j = 0; j < n - i; j++)//注意一开始i为0的话,j<n,j+1是可以越界访问的哦!
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
temp = 0;
}
}
if (temp)
break;
}
}*2.快速排序:
哈哈,全体起立!(`・ω・´),别的排序均是以其性质或者相关的某个性质起名的,而这个直接就是起名为快速排序,可见其含金量了吧~我在这里只实现快速排序的最初的版本,也就是hoare版本(递归版本)
思想&图解:
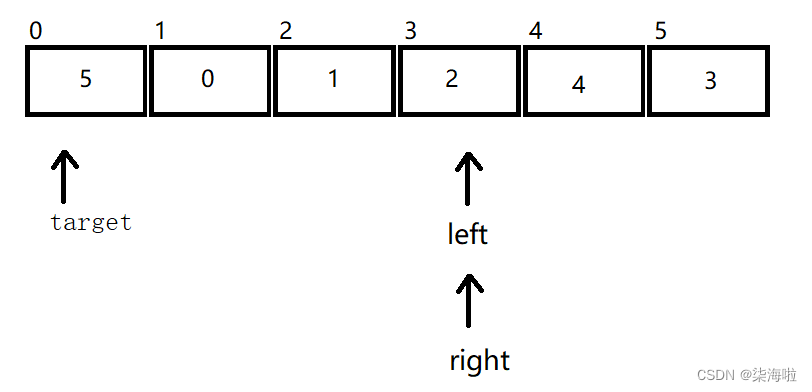
快速排序的这个版本里呢,我们首先需要定义一个目标地址target,这个地址所处的位置的数值接下来要排到属于它排序的所在位置,比如在2 5 1 0 4 3 中,第一个target位置是0,数据是2,那么接下来一轮排序完后,target的位置调到2中,也就是排完升序0 1 2 3 4 5的第三个位置,也就是排完顺序的位置。
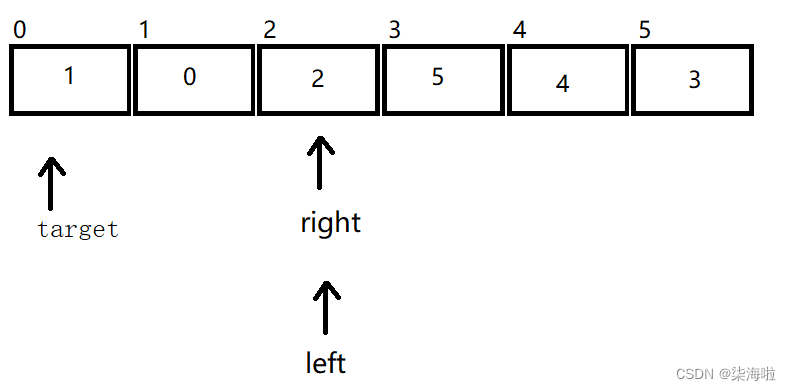
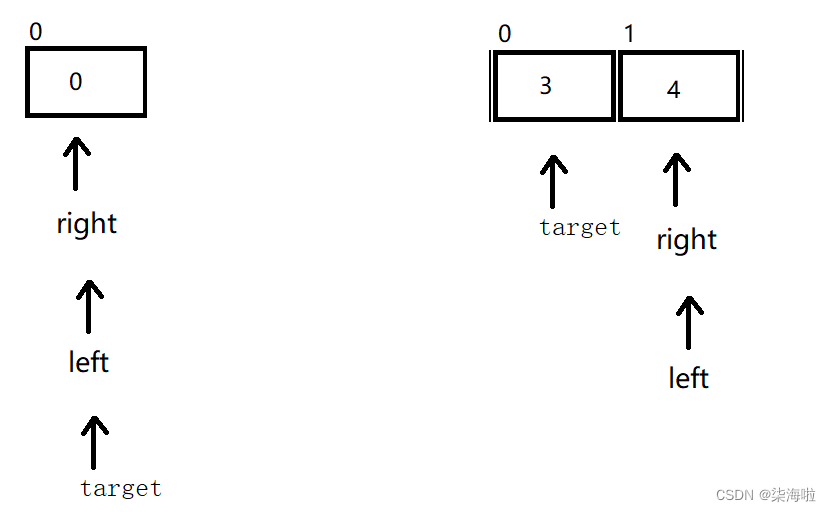
那么怎么找到2的位置呢?很简单,只需要目标地址外,分别定义两个地点,一个定义成left,从target+1开始,另一个定义成right,从数组末尾开始,让这两个分别朝向中间移动,知道他们相遇或者错过时,让右边的所有值大于target位置的数,让左边的所有值小于target位置的数。然后再他们相遇的位置和target交换。
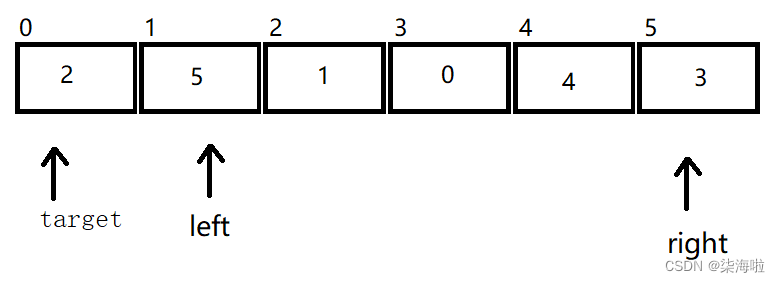
那么如何实现上面一段的效果呢?只需要right找小,left找大,两个分别找到后,对应数组位置交换数值,比如在2 5 1 0 4 3中,目标是2,right找到了5,left找到了0,那么两者所在位置的数组元素交换即可。*那么两个谁先走呢?
假设如果是左边先走,就以上面的为例:
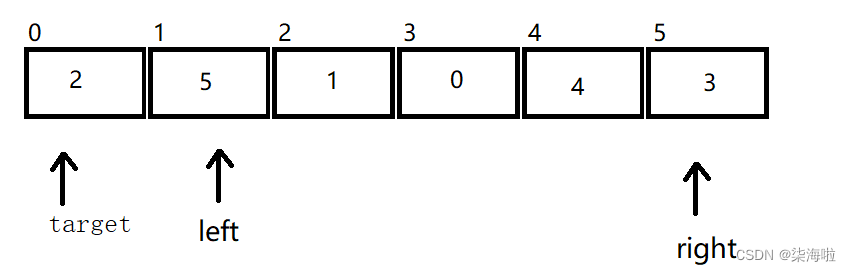
首先遇到5,比2大,停止运动,然后right找,找到0停止运动。
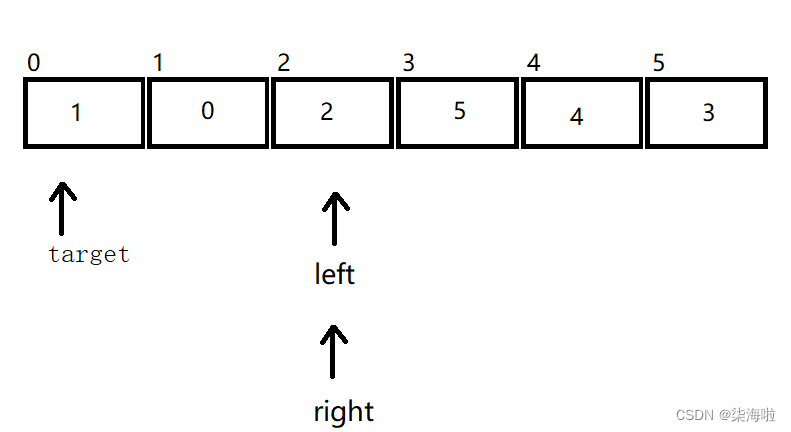
然后两者交换。left在往右找,找比2大的,找到了5,但是和right相遇了。此时相遇,所以target所在位置的数组元素和相遇处的数组元素值交换。
此时我们发现,2并没有在它该有的位置,所以,找左先走找大数无法满足要求。
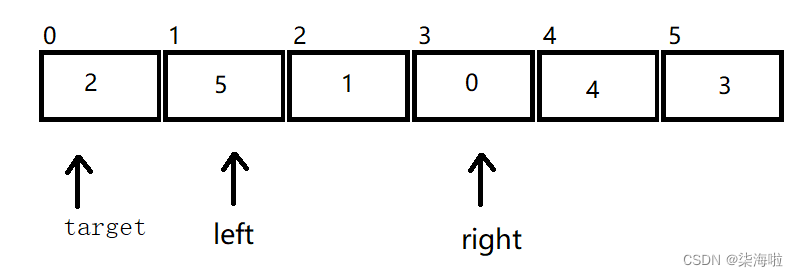
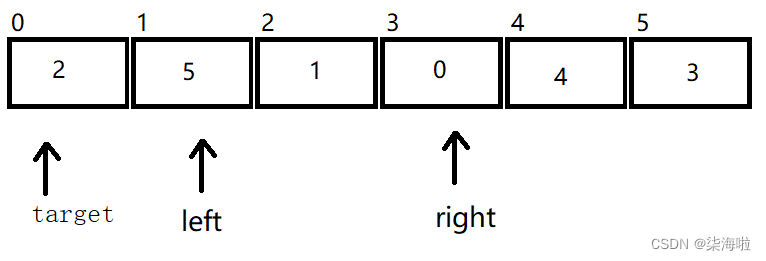
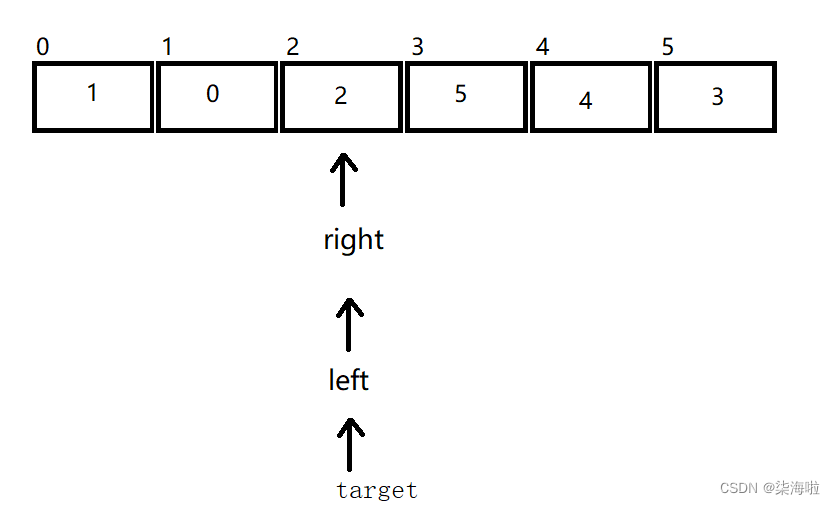
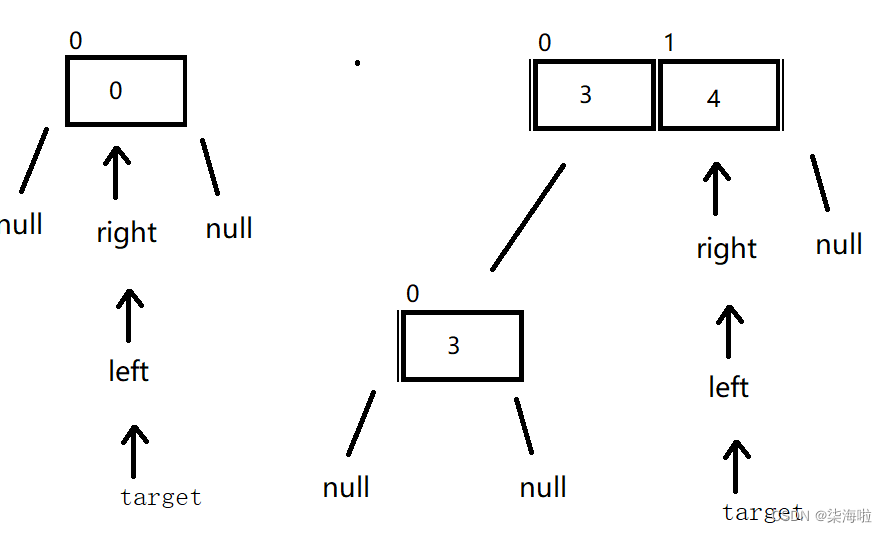
那么开始右边先走,以上面为例:
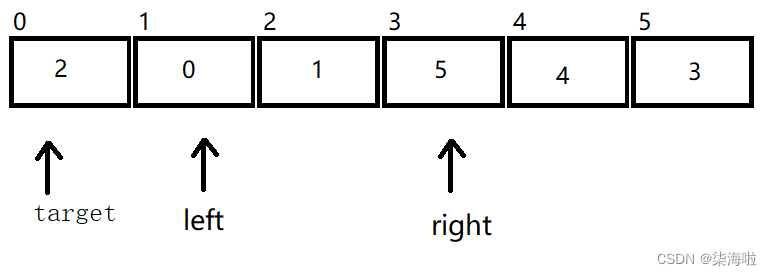
右边遇到比2小的停下来,然后左边开始动,5比2大,所以不发生位移。然后进行交换。
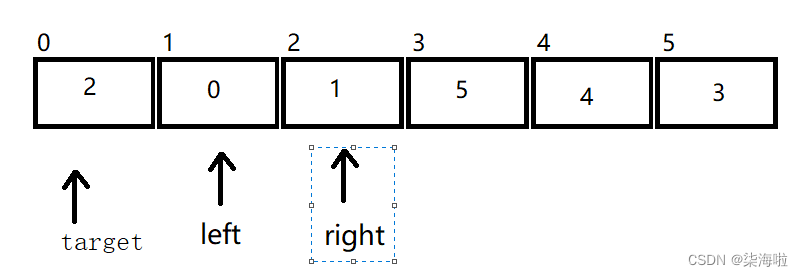
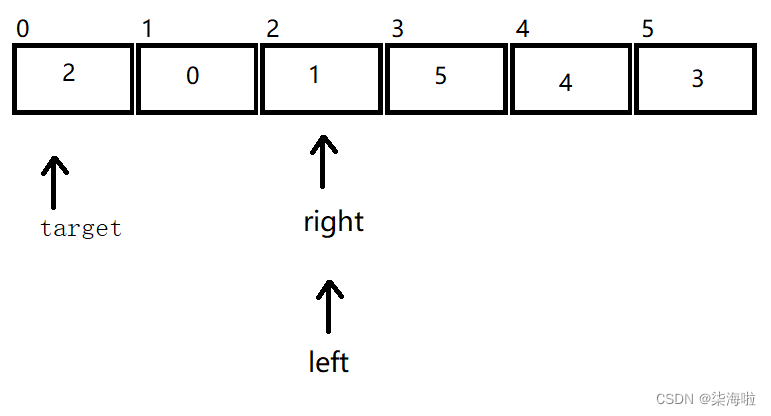
然后右边开始动,找到比2小的1停下来,然后左边开始动,与右边的相遇,然后和target位置的数字进行交换:
此时,我们发现,位子是正确的(交换后的元素左边均比它小,右边均比它大)。那么,为什么先动左边就错误呢?
我们可以发现,如果是左边先走的话,最后的位置可能就是比目标值大的所在数下标(left先遇到right),最后一个元素肯定是小的和目标值交换,所以只有right先走,最后要么left遇到right(此时right下是比目标值要小的),要么right遇到left(此时left之前和right交换过一次,比目标值小)。
综上,我们此排序是升序,要求左边到右边是从小到大,定义最左边为目标地址的话,说明最后一次交换必然是将比其小的到这里,所以,只要右边先走才能符合这种预期。
然后,这是第一轮,那么我们如何将整个数组的数排完呢?利用分而治之的思想。
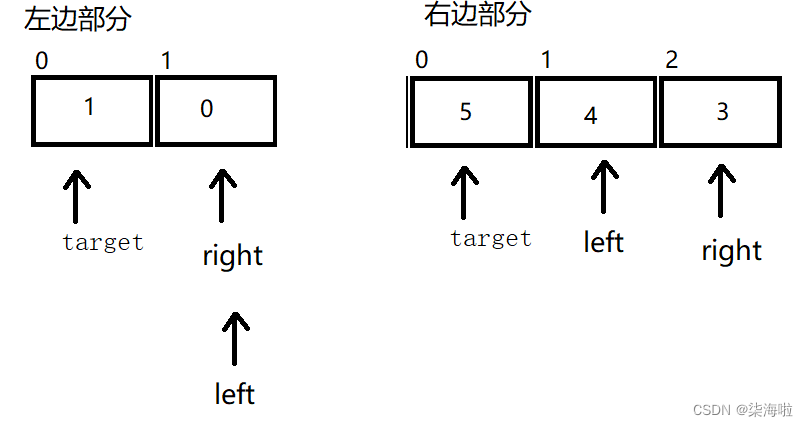
即每一次排完后,以target的位置作为分裂点,左边递归进去,视为左边部分排序好,然后右边部分递归进去,右边部分排序好,依次往下,直到传进去为空数组或者是一个数字的时候在回溯回来即可。下面用上面的简单数组来进行演示:
当前处于第一轮结束,然后我们将target左边部分进行递归,右边部分进行递归:
然后重复上面的排序过程:
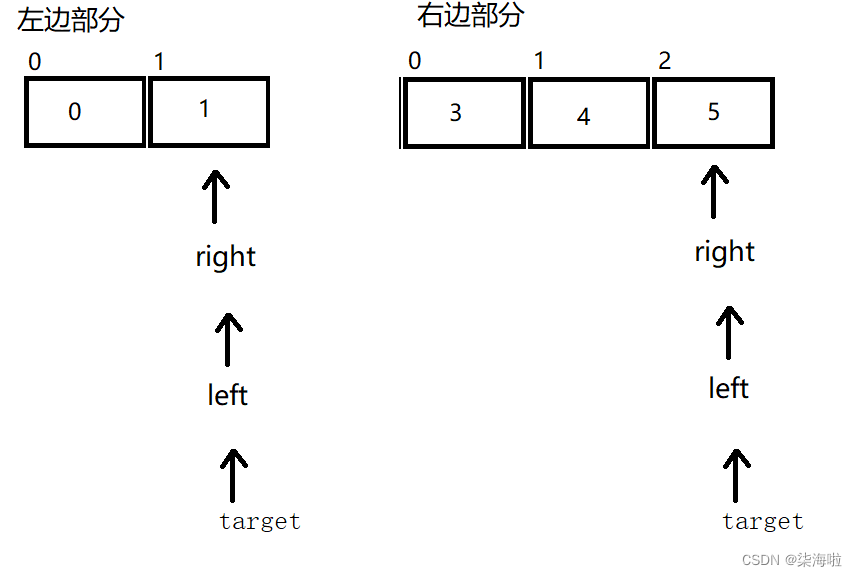
然后将target的左边传进去,右边传进去(马上出来,空数组):
此时我们发现,左边的已经不用排了,但是右边的观察一下,能否像我们之前那样直接交换吗?显然不能。因为此时这两个right和left一次循环都没有进过哦,所以,我们需要在交换时加上限制条件,防止出现此种意外。
然后继续上面的分治算法:
当全部的数回溯完毕后,数组自然而然就全部排序好啦!
实现:
实现来了哦٩(๑>◡<๑)۶
同样的,由上面的思路,我们首先将第一轮给复刻出来:
我们需要传入头位置和一个尾位置,所以形参自然是这两个和数组。第一轮定义最左边的为target,target+1为left,最后一个元素位置定义成right。
void QuickSort(int* a, int head, int end)
{
int target = head;
int left = target + 1;
int right = end;
}然后进入循环,循环的结束条件自然是相遇或者错过,那么就用right>left即可,然后右边先走,找到比target小的停下或者遇到left也停下,然后左边再找,找到比target大的停下,或者遇到right也停下。
while (right > left)
{
//右边先找,找到比target处的数字小的停下 下面经过画图分析,如果不加等号的话,就会陷入死循环~
while (right > left && a[right] >= a[target])
{
right--;
}
while (right > left && a[left] <= a[target])
{
left++;
}
}注意,此时那个大于等于的等于号是否可以不用加呢?假设不加:传入2 2 2 2 2 进来,会陷入死循环的哦~
然后就是区别于是否是停下left和right交换还是结束循环了的问题,也只需要加上一个限制条件进行交换即可。
if (right >left)
Swap(&a[right], &a[left]);然后结束循环,判断是否满足要交换的比targe位置小(判断targe是否已经在正确的位子上),进行交换(别忘了交换后targe = right让其定标到正确的位子上哦):
if (a[right] < a[target])
Swap(&a[target], &a[right]);然后进入分治,左边部分传入head,target-1,右边部分传入:targe+1,end。
QuickSort(a, head, target - 1);
QuickSort(a, target + 1, end);那么如何判断结束呢?只需要将传进来的head和end进行比较即可。head<end即可,不满足结束程序:
if (head >= end)
return;综上,快速排序hoare版本代码如下:
//快速排序:hoare版本(递归版本)
void QuickSort(int* a, int head, int end)
{
//结束标志
if (head >= end)
return;
assert(a);
int target = head;
int left = target + 1;
int right = end;
while (right > left)
{
//右边先找,找到比target处的数字小的停下 下面经过画图分析,如果不加等号的话,就会陷入死循环~
while (right > left && a[right] >= a[target])
{
right--;
}
while (right > left && a[left] <= a[target])
{
left++;
}
if (right >left)
Swap(&a[right], &a[left]);
}
if (a[right] < a[target])//防止传入的两个数,一次也不进入循环,然后无法判断和target位置所在数组元素大小的情况
{
Swap(&a[target], &a[right]);
target = right; // 一次不进循环target不能改变,否则上层进行分治的时候会出错
}
//进入递归,分而治之的思想
//左边
QuickSort(a, head, target - 1);
//右边
QuickSort(a, target + 1, end);
}
快速排序还有另外两种实现方法以及非递归和几种优化方案,详情可看这篇博客哦~
【c语言】快速排序的三种实现以及优化细节_快速排序的三种优化思路_柒海啦的博客-CSDN博客
三、插入排序
所谓插入排序,就是比如打牌的时候(斗地主),你这拿好牌后插入牌的操作一样,在一堆排好序的牌中插入。此就为插入排序。
1.插入排序
思想:
第一轮进来的数组,因为未知其是否有顺序,那么,就假设第一个数是有顺序的,从第二个数开始排。这里是升序,如果排入的数比排好里的数大的话就结束循环,比其小就继续循环。循环想要结束一种就是比其中一个排好的数大,要么就是与排好的数比完了,它就是最小的。
这里是内层循环,即每次插入需要走的循环。然后就是插入多少了,从数组的第二个数开始插入,插完后,就变成有序的了,然后继续往后走,走到末尾即完毕。
图解:
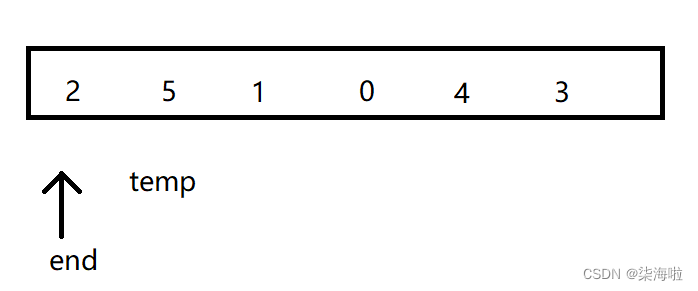
仍然以2 5 1 0 4 3为例子:
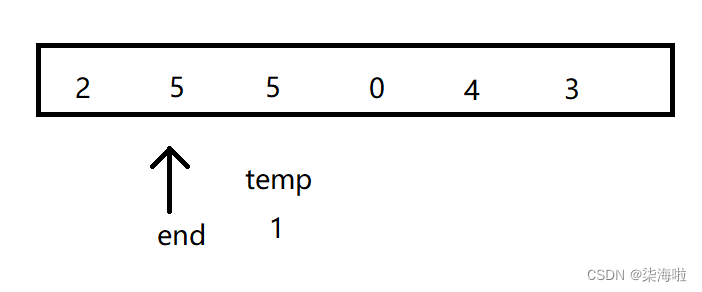
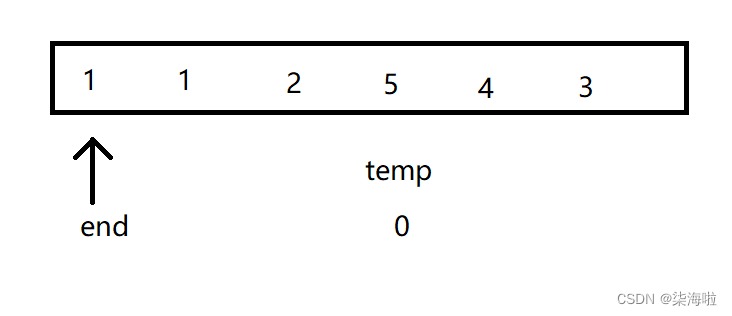
为了便于外层循环和内层循环时用于区分从哪里开始和赋予值,我们可以定义一个end来储存排好序的尾部,temp表示要插入的元素(temp直接储存元素,而不是存储下标),第一次进入的时候,如图:
然后两者相比,temp>end跳出循环(因为插入的已经是排序好的,既然第一个不用变化后面的自然也不用变化。这正是插入排序的优势,也是后面希尔排序所利用的关键之点)
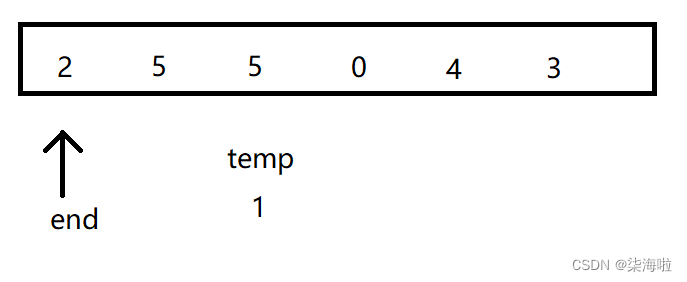
然后end = i(外层循环i++),temp = a[end + 1],继续插入:
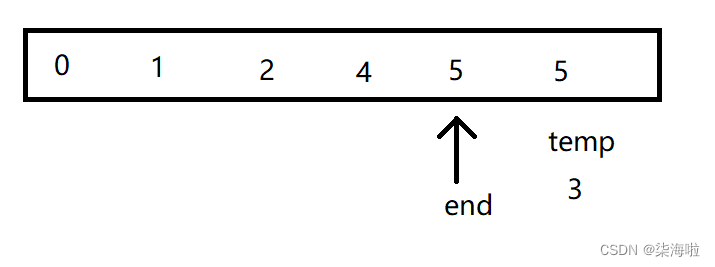
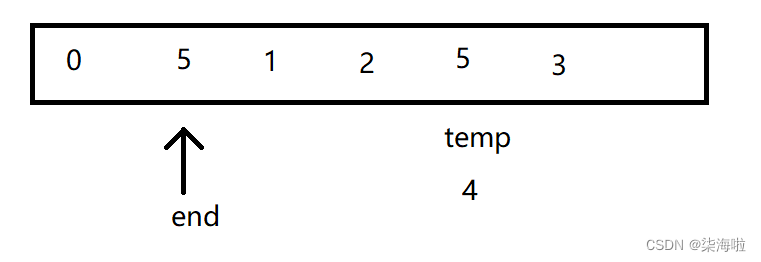
然后开始插入,发现temp的值比end所在数组元素的值小,开始往后排(类比于插入动作)
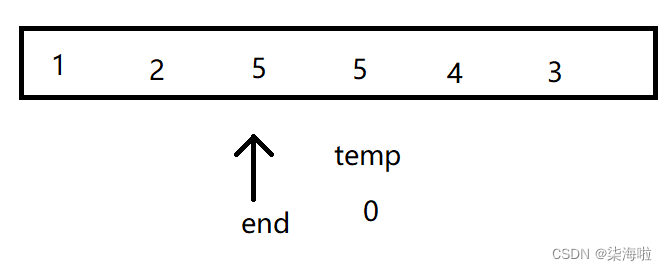
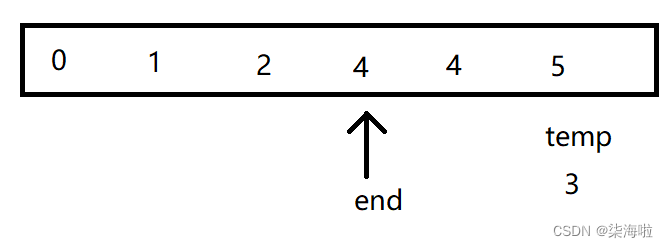
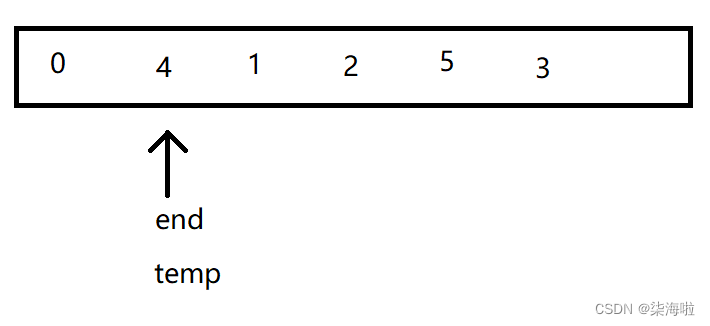
然后,end--,查看下一个:
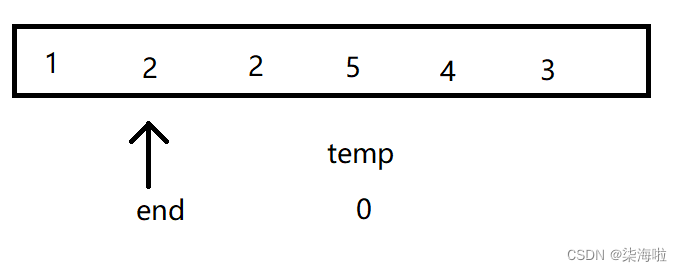
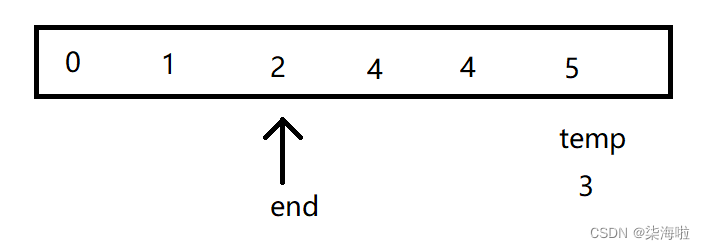
发现比其大,继续向后排:
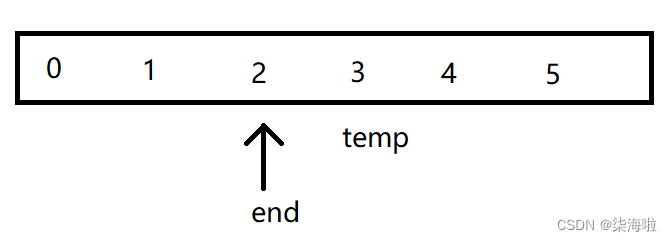
然后end--,发现小于0了,跳出内层循环,将temp的值赋给a[end + 1]即可。
(end == -1)
然后end从外层循环获得i(尾巴)即2,temp=a[end + 1] = 0,继续上述步骤:
(end == -1)
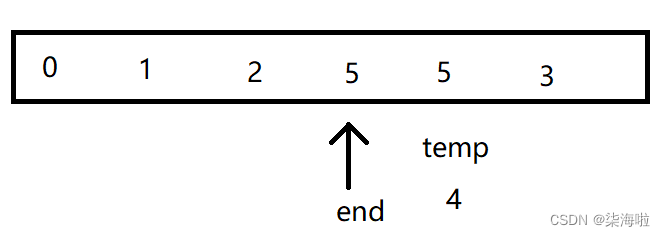
然后,end = i(i++),获得尾部下标:3,temp = a[end + 1] = 4。继续上面的操作:
注意,此时检测到要比temp小,所以跳出循环,将a[end + 1] = temp即可。
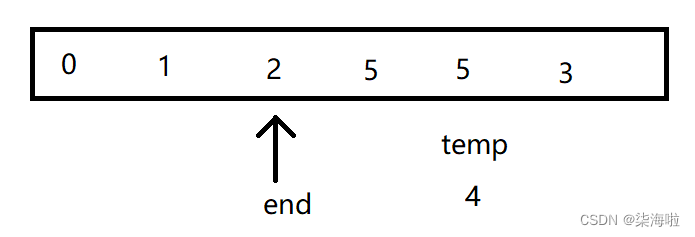
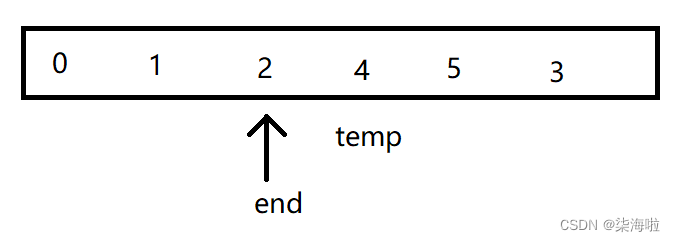
然后end = i(i++)获得尾部下标:4,temp = a[end + 1] = 3,重复上述步骤:
此时跳出循环,a[end + 1] = temp即可。
然后i++越界了,外层循环结束。程序结束,插入排序完成!
实现:
我们首先实现一开始以第一个为排好了的末尾,第二个元素开始插入的算法:老规矩,传入的形参是数组和数组个数,然后end = 0,temp=a[end+1];
void InsertSort(int* a, int n)
{
int end = 0;
int temp = a[end + 1];
...
}然后进入内层循环,以end>=0为判断是否进入循环的条件,如果a[end] > temp,往后退,即就是前一个覆盖掉后一个即可,如果不满足,就跳出循环。我们发现跳出循环(正常结束或者break后)此时end + 1的位置均是插入的位置,因此,代码如下:
while (end >= 0)
{
if (temp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = temp;然后加一个外层循环即可,i从0开始,最后一个自然就是n - 2,因为temp = a[end + 1]小心越界哦~
for (int i = 0; i < n - 1; i++)
{
int end = i;
int temp = a[end + 1];
...
}
...综上,插入排序的实现代码是:
//插入排序,核心思想:来插入的数字和排好了的数字进行比较,插入到比其小的前面,大的后面。按照升序的话,新来的率先就要和最大的数进行比较,
//如果比起小,那么依次往后排,知道比其大,结束循环,比其大的依次往后移出来一步,然后插入即可。
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;
int temp = a[end + 1];
while (end >= 0)
{
if (temp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = temp;
}
}2.希尔排序
思想&图解:
可以这么理解,希尔是对插入排序的补全。
结合插入排序的实现思路,其实不难发现,只要我们需要排序的数字越有序,插入排序就排的越快。因此,希尔排序就此,给插入排序引入预排序。
这个预排序可不简单,我们可以对需要排序的数组决定每一步走几个,像正常的插入排序就是1步,那么,我们可不可以在预排序的时候定义走3步呢?
如下:
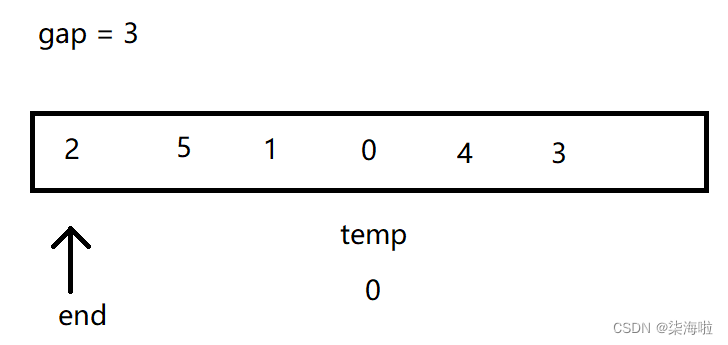
gap用来定义走的步数,所排序的数组依然用上面的2 5 1 0 4 3
gap = 3;
从0开始,temp = a[end + gap];
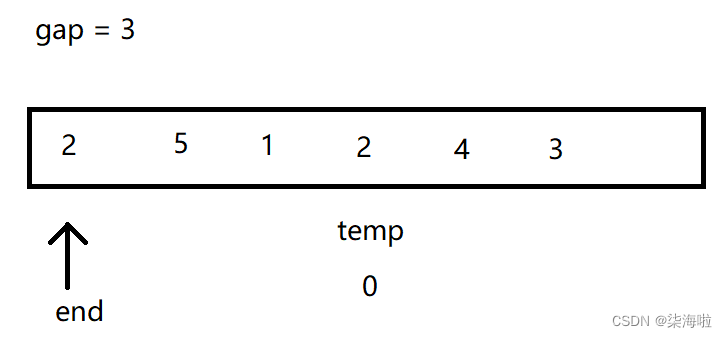
然后将像插入排序那样进行排序:temp<a[end],所以往后排:
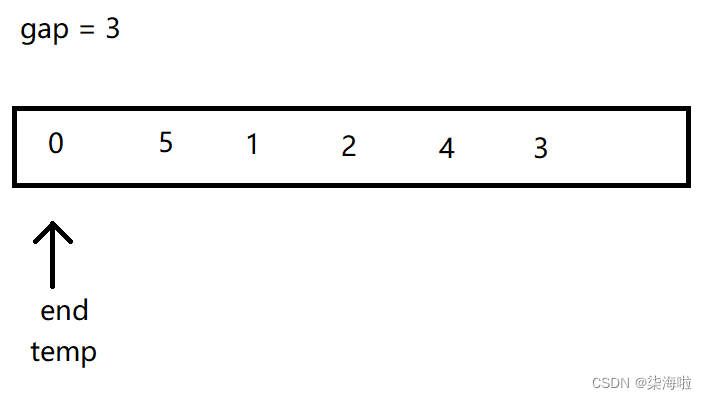
然后end-gap,发现小于0,退出循环,然后a[end + gap] = temp,即:
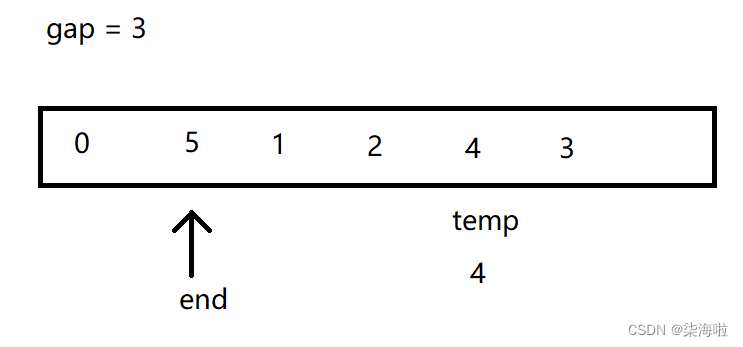
但是此时,第一轮并没有结束哦~,然后end = 2,从2开始,重复上面步骤:
end = 3,继续上述步骤:
此时第一步都没进去,什么都不变。此时我们发现temp已经到最后一个元素了,end在加一的话,end +gap就要越界访问了,说明此时的插入排序的外层循环应该是i<n - gap.
而内层循环里面end--就自然是end-gap了。
此时,这三个排完后,我们发现0 4 1 2 5 3相对于原来的2 5 1 0 4 3是不是变得更加有序的一点了呢?此时在gap = 2,最后gap = 1是不是就可以更加快速的排序了。所以,我们要控制gap的取值了,这里以n为基准,以广为用的gap = gap/3 + 1为控制语句,gap>1为循环条件即可。即可实现希尔排序。
实现:
首先,先将图解的gap = 3那一步用代码实现。
基本步骤和插入排序一样,只不过每一次end改变就是end - gap,并且一开始end = 0,一直边到n - gap为止,temp获得下标应该是end + gap即可。
gap = 3;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int temp = a[end + gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = temp;然后控制gap语句,由思路里面讲的,gap每/3进行变化,那么为什么加1呢?因为,最后一次需要以1步进行变化,这样才能最终排好序,但是必须保证1的存在,否则比如2/3这样的就不会出现1,所以就会加1保证最后一次循环是gap = 1进行循环,也就是插入排序:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
...
}
}综上,希尔排序的总代码为:
//希尔排序 对插入排序的改进
//出色的原因是 首先进行多组预排序,预排序之后,会越来越接近于正确的排序,而这组数越接近于正确的顺序,插入排序就越快!所以,效率提升显著!
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//gap = gap / 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int temp = a[end + gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = temp;
}
}
}
欢迎大家指正哦!!!,我们一起学习共同进步吧!加油呀٩(๑❛ᴗ❛๑)۶ヾ(✿゚▽゚)ノヾ(◍°∇°◍)ノ゙ヾ(๑╹◡╹)ノ"(๑´ㅂ`๑) (๑*◡*๑)٩(๑>◡<๑)۶ (๑╹◡╹)ノ"""(๑´ㅂ`๑)




































 179
179











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








