一)回文子串:
思路1:暴力枚举:
for(int i=0;i<array.length;i++)
for(int j=i;j<array.length;j++)
我们的中心思路就是枚举出所有的子字符串,然后进行判断所有的子串是否是回文串
每一次我们固定i位置,j向后走,就成功枚举出了以i位置为起点的所有回文字串的情况,将i进行++,然后再让j从i位置进行++
思路2:中心扩散:
如果以单个字符为中心向两边进行中心扩展,那么最终扩展完成之后的回文串长度都是奇数个,如果以两个字符为中心向两边进行中心扩散,那么最终扩展完成之后的回文串的长度都是偶数个,这两种方法相当于是枚举了所有的子串
class Solution { public int countSubstrings(String s) { char[] array=s.toCharArray(); int ret=0; for(int i=0;i<s.length();i++){ ret+=check(array,i,i); ret+=check(array,i,i+1); } return ret; } public int check(char[] array,int left,int right){ int count=0; while(left>=0&&right<array.length&&array[left]==array[right]){ left--; right++; count++; } return count; } }
思路3:动态规划
回文串问题是用动态规划解决可以进行判断能够将所有的子串是否是回文的信息,保存在dp表里面,首先进行考虑的是我们的状态标识该如何找到所有的子串
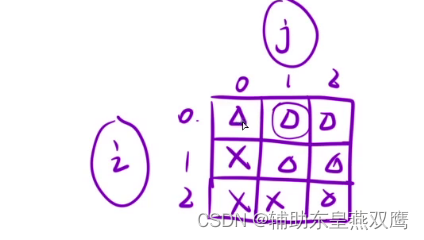
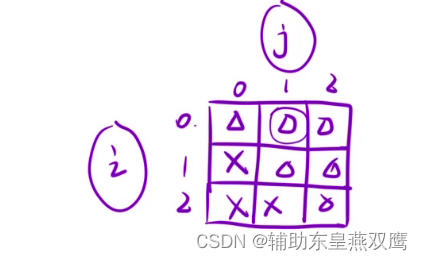
dp[i][j]表示以i位置为起点,j位置为中点的子串,是否是回文串,横坐标表示起始位置,纵坐标表示结束位置
因为i是小于j的, 所以我们的dp表只会使用到对角线以及上三角所在的部分(i>=j)
3.1)如果array[i]!=array[j]那么从i位置到j位置的这段字符串,一定不是回文串
3.2)如果array[i]==array[j],又是分成三种情况:
if(i==j) dp[i][j]=true
else if(i+1==j) dp[i][j]=true
else dp[i][j]=dp[i+1][j-1]
进行填表的时候只是会用到上三角的值,从下向上填表,从左向右进行填表
dp[i][j]是以i位置和j位置元素为结尾的字符串是否是回文串,但是如果是i==j的情况,或者是i+1==j的情况,如果还是使用状态转移方程dp[i][j]=dp[i+1][j-1]这种方法来搞的话,此时j下标就会跳到i下标的前面,此时就和我们的状态表示发生了冲突
初始化:不用初始化
填表顺序:从下向上,每一行,因为当进行填写当前行的时候要使用到下一行的值
返回值:返回的是dp表中true的个数
class Solution { public int countSubstrings(String s) { int count=0; char[] array=s.toCharArray(); boolean[][] dp=new boolean[array.length][array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){//保证j在i后面 if(array[i]==array[j]){ dp[i][j]=i+1==j||i==j?true:dp[i+1][j-1]; }else{ dp[i][j]=false; } if(dp[i][j]==true) count++; } } return count; } }二)最长回文子串:
先进行判断这个子串是否回文,然后再次进行统计所有子串的个数
填表顺序:用当前位置的值需要使用到下一行位置的值,所以需要从下向上进行填表即可
返回值:dp值是true的情况下,返回长度最大的字串的起始位置以及长度
class Solution { public String longestPalindrome(String s) { char[] array=s.toCharArray(); int maxlen=-1; String maxString=""; boolean[][] dp=new boolean[array.length][array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ dp[i][j]=(j==i+1||i==j)?true:dp[i+1][j-1]; if(j-i+1>=maxlen){ maxString=s.substring(i,j+1); maxlen=j-i+1; } }else{ dp[i][j]=false; } } } return maxString; } }三)回文串分割:
暴力枚举:将所有的三元组字符串给进行枚举一下,将所有的分割出来的三个字符串给进行枚举一下,只要枚举完成,只需要将三个字符串都进行判断一下是否是回文即可
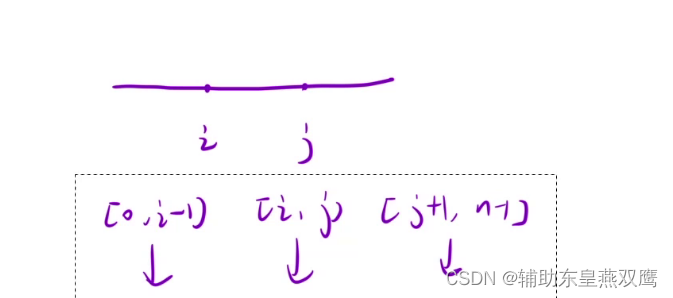
我们将整个字符串分割成三部分:
我们设i是第一个字符串的起始位置,j表示第二个字符串的终止位置,可以枚举第二个字符串的起始位置和终止位置
class Solution { public boolean checkPartitioning(String s) { //1.利用dp来进行检查一下所有的子串是否回文 char[] array=s.toCharArray(); boolean[][] dp=new boolean[array.length][array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ dp[i][j]=i+1==j||i==j?true:dp[i+1][j-1]; }else{ dp[i][j]=false; } } } //2.枚举第二个字符串的所有的起始位置和终止位置 for(int i=1;i<array.length;i++){//既然是枚举第二个字符串,那么前一个字符串必须得存在 for(int j=i;j<array.length-1;j++){//至少要给最后一个字符串枚举 if(dp[0][i-1]==true&&dp[i][j]==true&&dp[j+1][array.length-1]==true){ return true; } } } return false; } }
四)分割回文串:
1)定义一个状态表示:
dp[i]表示以字符串i为结尾最长的子串的最少分割次数
2)根据状态标识推导状态转移方程
1)快速确定某一个字符串的子串是否是回文串
2)可以创建一个二维dp表,将所有的子串是否是回文的信息,保存到hash表里面
j==0的时候,0-i位置的字符传是否是回文子串已经考虑过了
j==i的时候,起始位置就是最后一个字符
3)如果0-i区间内的字符串是一个回文串,就不需要进行切割,那么我们就设j为最后一个字符串的起始字符,如果0-i区间内的字符串不是回文串,我们就想一下如果0-j区间内的字符串能够被分割成一个回文串况且有最小分割次数,况且dp[j][i]是一个回文串,那么此时dp[i]=dp[j-1]+1;
4)j>=0&&j<=i,如果j==0的话,那么那么表示j是第一个字符串的起始位置,已经被dp[i]考虑过了,所以j的取值范围就是j>0&&j<=i
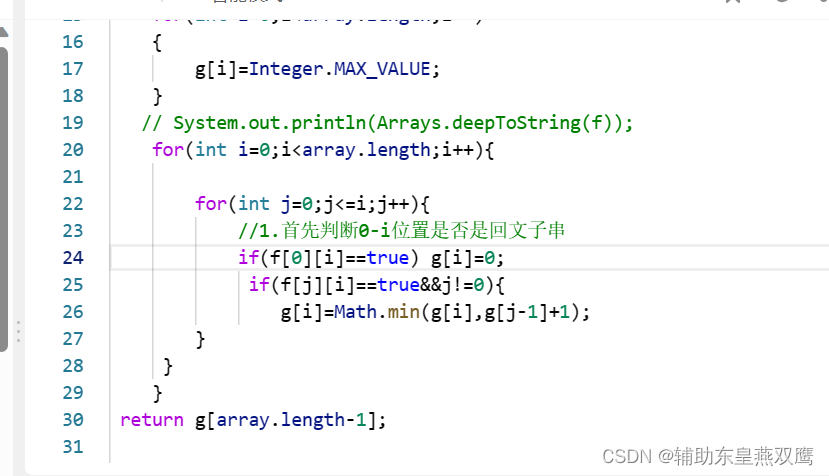
如果判断f[0][i]的逻辑写到循环里面
dp[i]=Math.min(dp[j-1]+1,dp[i])为了使我们再进行第一次进行比较的时候dp[i]的之不要去干扰我们第一次比较的结果,可以让dp[i]全部初始化成Integer.MIN_VALUE
在进行填写dp[i]的时候,至少要保证dp[j-1]已经被初始化完成了,所以填表顺序是从左向右
上面代码块这么写会导致进行计算f[0][0]的时候计算错误
public int minCut(String s) { //1.先将这个字符串进行预处理,将字符串中每一个子字符串是否是回文串的信息存放到一个二维的dp表里面 char[] array=s.toCharArray(); boolean[][] f=new boolean[array.length][array.length]; int[] g=new int[array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ f[i][j]=i==j||i+1==j?true:f[i+1][j-1]; }else{ f[i][j]=false; } } } //2.然后再次进行字符串拆分 for(int i=0;i<array.length;i++) { g[i]=Integer.MAX_VALUE; } // System.out.println(Arrays.deepToString(f)); for(int i=0;i<array.length;i++){ for(int j=1;j<=i;j++){ //1.首先判断0-i位置是否是回文子串 if(f[0][i]==true) g[i]=0; else if(f[j][i]==true){ g[i]=Math.min(g[i],g[j-1]+1); } } } return g[array.length-1]; }
五)最长回文子序列
一)定义一个状态表示:
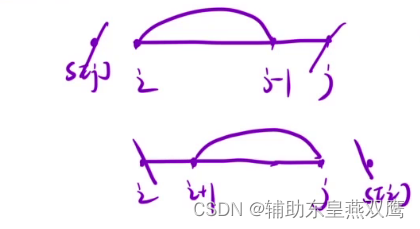
1)以i位置元素为结尾的所有子序列中最长的回文子序列的长度,如果这样定义状态标识,根本推不出状态转移方程,如果以i位置为结尾,势必就会使用到i-1,i-2等等位置的dp值来更新当前i位置的dp值,假设我们就举一个例子,dp[i-3]表示以i-3位置为结尾的最长回文子序列的长度,但是我只是知道以i-3元素为结尾的回文子序列的长度,我连i位置的元素是否可以和i-3位置的元素是否能够构成回文子序列都不知道,请问我该如何更新dp[i]的值呢?是永远无法更新出最长回文子序列的长度,首先得知道是否能够成回文子序列?根本判断不出来,根本不能由前面的状态来推导出dp[i]的值,从下图所示可以看出,从[i,j]这段区间内最长回文子序列的长度可以推导出[i+1,j+1]这段区间内最长回文子序列的长度
二)根据状态标识推到状态转移方程
根据最后一个位置推导问题(i<=j)
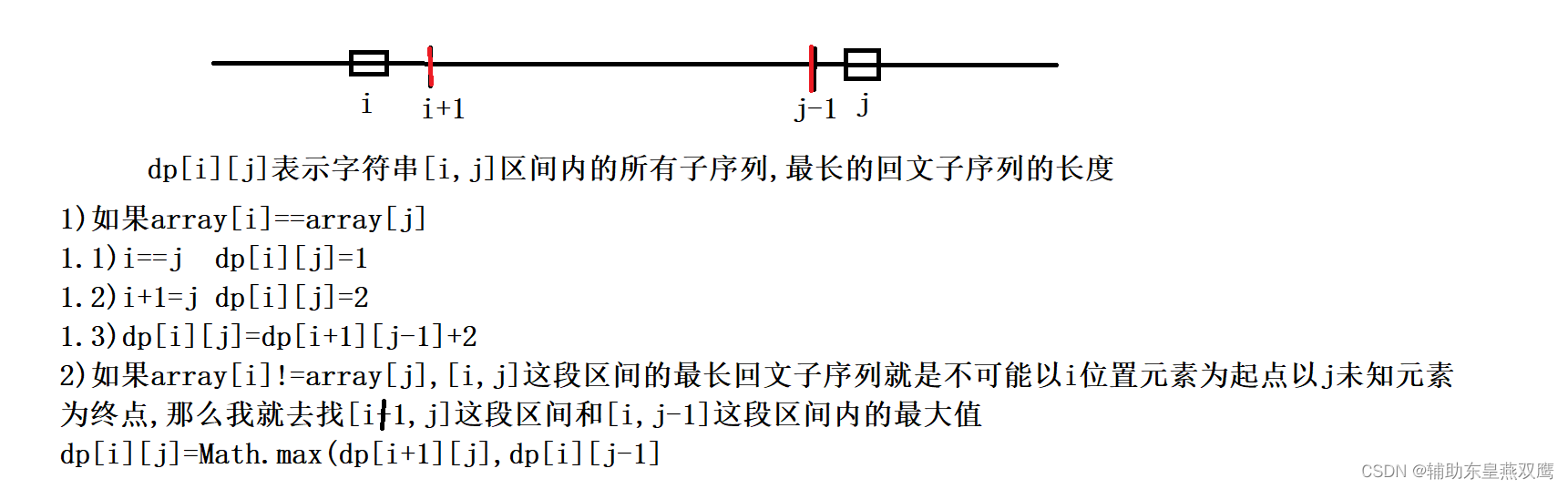
1)dp[i][j]是以i位置元素为起点,j位置元素为终点的最长回文子序列
2)如果i位置的元素等于j位置的元素,此时i==j,此时最长回文子序列就是1,如果i+1=j,说明此时i和j两个位置的元素是相邻的,此时最长回文子序列就是2,如果i位置和j位置中间包含多个元素,那么dp[i][j]=dp[i+1][j-1],最长回文子序列一定是包含以ij位置为结尾的
3)如果i位置元素和j未知元素不相等,那么dp[i][j]最长回文子序列不可能是同时起点是i,终点是j,那么此时就去i+1到j和i到j-1去找回文子序列的最大值
4)补充:为什么要考虑i==j和i+1==j的情况呢?就是为了让状态转移方程满足dp[i][j]的含义
三)初始化,填表顺序,返回值
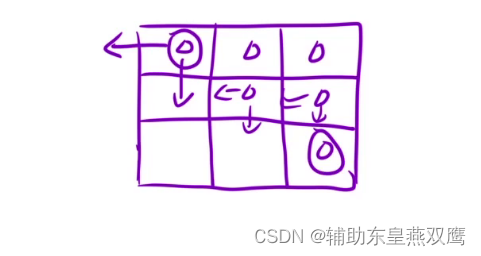
初始化:我们在进行初始化的时候只会使用到对角线以及对角线以上的值
1)当我们进行填写第一个三角格子的时候,dp[i][j-1]可能会发生越界,此时i=0,j=0
2)当进行填写最下面的圆圈的时候,dp[i+1][j]可能会发生越界,此时i==j==n,但是这种情况我们在上面已经考虑过了,所以不需要进行初始化
3)正常来说,除了这两个位置,这个dp值只会依赖左边的值和下面的值,都不会发生越界
所以越界的情况都已经在dp表中考虑过了,所以我们就不需要进行初始化了
4)从下向上进行填表,每一行从左向右
填表顺序当进行填写dp表的时候,进行填写到dp[i][j]的时候,需要dp[i+1][j]的值,需要使用到下一行的值和dp[i][j-1]需要用到左边的值,所以填表顺序就是从下向上,从左向右
返回值:返回dp[0][array.length-1]里面的值
class Solution { public int longestPalindromeSubseq(String s) { char[] array=s.toCharArray(); //1.dp[i][j]表示以i位置为开头,j位置元素为结尾最长回文子序列的长度 int[][] dp=new int[array.length][array.length]; //2.进行填写dp表,从下向上进行填表 for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ if(i==j) dp[i][j]=1; else if(i+1==j) dp[i][j]=2; else dp[i][j]=dp[i+1][j-1]+2; }else{ dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]); } } } return dp[0][array.length-1]; } }
六)让字符串成为回文串的最少插入次数
做回文串的题的时候,状态表示都是选取一段区间来进行研究问题
默认情况下就是i<=j的
一)定义一个状态表示
dp[i][j]表示s字符串内[i,j]这段区间内的子字符串使它成为回文串的最小插入次数
二)根据状态表示推导状态转移方程
从i和j位置根据最近的一步划分问题,当i==j的时候,我们只需要找到i-1,j-1字符串成为回文串的最小插入次数即可
class Solution { public int minInsertions(String s) { char[] array=s.toCharArray(); int[][] dp=new int[array.length][array.length]; //1.dp[i][j]表示以i位置为起点,j位置为终点得是这段区间成为回文串得最小插入次数 for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ if(i==j) dp[i][j]=0; else if(i+1==j) dp[i][j]=0; else dp[i][j]=dp[i+1][j-1]; }else{ dp[i][j]=Math.min(dp[i+1][j]+1,dp[i][j-1]+1); } } } return dp[0][array.length-1]; } }









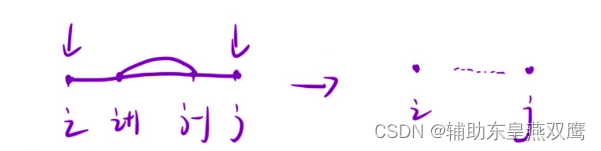




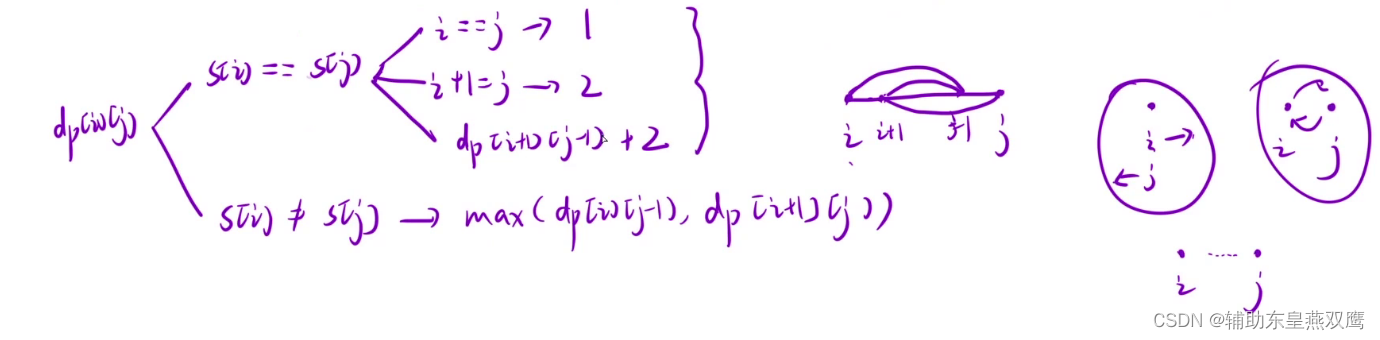
















 1361
1361











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








