python解决折叠加密问题

简单记录一下作业完成，怕哪天手贱把代码删了QAQ

直接上代码：（不过这代码只记录了一种加密解密方式，但有这一种方式加上理解足够想出其他方式的加密解密了）

def encode(str, n):
    regl1 = ['']*n
    regl2 = ['']*n
    string = ['']*2**n
    string[2**n-1] += str
    d = 2
    for i in range(1, n+1):
        print(f"第{i}次折叠")
        regl1[i-1] = input("左右/右左 (0/1):")
        regl2[i-1] = input("向上/下 (0/1):")
        if regl1[i-1] == '0' and regl2[i-1] == '0':
            c = 0
            for j in range(0, 2**(i-1)):
                string[2**n-d+j] = string[2**n-j-1][:int(len(string[2**n-j-1])/2)][::-1]
                string[2**n-j-1] = string[2**n-j-1][int(len(string[2**n-j-1])/2):]
                c += 1
            print(string)

def decode(str, n):
    regl1 = ['']*n
    regl2 = ['']*n
    string = str
    d = 0
    for i in range(0, n):
        print(f"第{i+1}次折叠")
        regl1[i] = input("左右/右左 (0/1):")
        regl2[i] = input("向上/下 (0/1):")
        if regl1[i] == '0' and regl2[i] == '0':
            for j in range(2**(n-i-1)):
                string[j+d] += string[2**n-j-1][::-1]
                string[2**n-j-1] = ''
            d += int(2**(n-i)/2)
            print(string)

if __name__ == '__main__':
    sel = input("加密/解密 (1/2):")

    if sel == '1':
        str = input("请输入长度为2^k(k<=8)的字符串：")
        n = int(input("折叠次数："))
        encode(str, n)
    else:
        n = int(input("折叠次数："))
        str = ['']*2**n
        for i in range(2**n):
            str[i] = input(f"第{i+1}层字符串：")
        decode(str, n)

先说一下基本思路（下面的折叠方向都以从左向右，向上折叠）：

1.假设我们要折叠  abcdefgh 这一串字符串。第一次折叠后变成

dcba

efgh

这是两个字符串，所以我就想用python的列表，因为列表里能存多个字符串。

2.折叠后发现层数也增加乐，就像是叠叠乐一样，所以想到可以把初始字符串作为地基，通过不断地折叠，在地基上不断地建层。

加密：

if __name__ == '__main__':
    sel = input("加密/解密 (1/2):")

    if sel == '1':
        str = input("请输入长度为2^k(k<=8)的字符串：")
        n = int(input("折叠次数："))   
        encode(str, n)

这基本都能看懂，而n是是来决定列表应该扩大多少。像是一开始就决定要建多少层，后面才能一层一层塞东西。

接下来再讲解加密过程。

def encode(str, n):
    regl1 = ['']*n       
    regl2 = ['']*n          #这两个数组用来决定折叠方向
    string = ['']*2**n      #建立含有2的n次方字符串的列表
    string[2**n-1] += str   #将初始字符串至于列表的最低层 
    d = 2                     #这个d是我多次测试出来的，用于后面的计算
    for i in range(1, n+1):    #这个for循环由之前的折叠次数决定
        print(f"第{i}次折叠")
        __author__ = 'winglet'
        regl1[i-1] = input("左右/右左 (0/1):")
        regl2[i-1] = input("向上/下 (0/1):")
        if regl1[i-1] == '0' and regl2[i-1] == '0':
            c = 0
            for j in range(0, 2**(i-1)):       
                string[2**n-d+j] = string[2**n-j-1][:int(len(string[2**n-j-1])/2)][::-1]
                string[2**n-j-1] = string[2**n-j-1][int(len(string[2**n-j-1])/2):]
                c += 1
        d *= 2
            print(string)

 1.

    string = ['']*2**n
    string[2**n-1] += str 

这段就是通过n的值来扩大列表的内容，后面字符串都以：abcdefgh  举例

第一次折叠

dcba

efgh

第二次折叠

fe

cd

ba

gh

发现每折叠一次，层数都是2的n次方，所以我们在一开始就要决定这个列表能储存多少字符串。这样才能在折叠时把字符串放在相应位置。

接着就是设置一个基底，我选择把初始字符放在基底就类似:

[ ]

[abcdefgh]

后面折叠时就可以把相应的字符串放上层。

2.

    d = 2 
    for i in range(1, n+1):
        print(f"第{i}次折叠")
        regl1[i-1] = input("左右/右左 (0/1):")
        regl2[i-1] = input("向上/下 (0/1):")
        if regl1[i-1] == '0' and regl2[i-1] == '0':
            c = 0
            for j in range(0, 2**(i-1)):       
                string[2**n-d+j] = string[2**n-j-1][:int(len(string[2**n-j-1])/2)][::-1]
                string[2**n-j-1] = string[2**n-j-1][int(len(string[2**n-j-1])/2):]
                c += 1
        d *= 2
            print(string)

为什么要设个d=2，这是我多次测试找到的，后面再讲解

第一个for循环，就不讲了，它按设定的折叠次数决定

后面才是重头戏

经过之前的手动折叠，我们能发现，每次折叠字符串的一半会留在原层，另一半会变成倒序并且与原层对称的位置储存。比如：

fe

cd

ba

gh

fe 与 gh 是一组的

cd 与 ba 是一组的

所以就能明白，我们要找到每组对称的位置再把相应字符放进去

           for j in range(0, 2**(i-1)):       
                string[2**n-d+j] = string[2**n-j-1][:int(len(string[2**n-j-1])/2)][::-1]
                string[2**n-j-1] = string[2**n-j-1][int(len(string[2**n-j-1])/2):]
                c += 1
        d *= 2

 所以这里的for作用就显而易见了，对每层的字符串进行重新分层，比如第一次折叠，只有一层字符串，那就只分一次就行，而第二次时已经有两层了，所以就要两次分

2**n - j -1  就是从底层开始向上 一组一组的分

2**n -d + j  就是查找2**n - j - 1的对应层

至于d为什么为2，你可以手动分层后数数每次折叠的对应层是多少

接着给对应层赋值就行

结果如图：

 

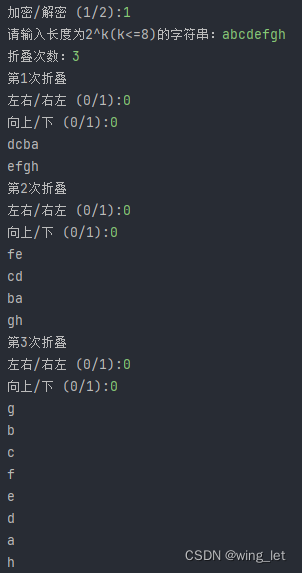
 解密其实也差不多