前言:求解最大公约数从高中一直到现在,始终是数学与程序设计的经典。现在,让我们看看GCD的四种解法

定义⋙
约数/因数(Divisor): 整数b除以整数a(b≠0) 除得的商正好是整数而没有余数,我们就说b能被a整除,或a能整除b。即:定义正整数a、b,有 b mod a=0,则称a为b的约数
倍数(multiple):一个整数能够被另一个整数整除,那么这个整数就是另一整数的倍数。即:定义正整数a,b,有b mod a=0,则称b为a的倍数
最大公约数【Greatest Common Divisor(GCD)】:也称最大公因数,最大公因子,指两个或多个整数共有约数中最大的一个。
a,b的最大公约数记为(a,b);
a,b,c的最大公约数记为(a,b,c)
最小公倍数【Least Common Multiple】:指两个或多个整数公有倍数中除零外最小的一个
a,b的最大公约数记为[a,b];
a,b,c的最大公约数记为[a,b,c]
问题描述⋙
给你两个正整数a、b,求a、b的最大公约数和最小公倍数,设已知a≧b
💥补充:[a,b]=a × b ÷ (a,b)
所以,我们只要求出a,b的最大公约数,最大公倍数便可直接求出
✨✈✈✈✈✈✈✈✈✈✈✈✈✈✈🛫🛫🛫🛫🛫🛫🛫🛫飞行分割线
1:朴素枚举法⋙
要求a、b的最大公约数,我们可以从大到小枚举a的约数,然后再判断它是不是b的约数,不断枚举,直到找到满足条件的最大公约数
[1]朴素枚举C/C++代码实现如下🌀
int gcd(int a,int b){
int mi=min(a,b);
int mx=max(a,b);
for(int i=mi;i>=2;i--){ //最好从两数中的较小者
if(mi%i==0&&mx%i==0) //开始枚举,以减少不必要的计算
return i;
}
return 1;
}
[2]朴素枚举法:流程图😈:
注:如果题目没给a、b的大小关系,加条补充
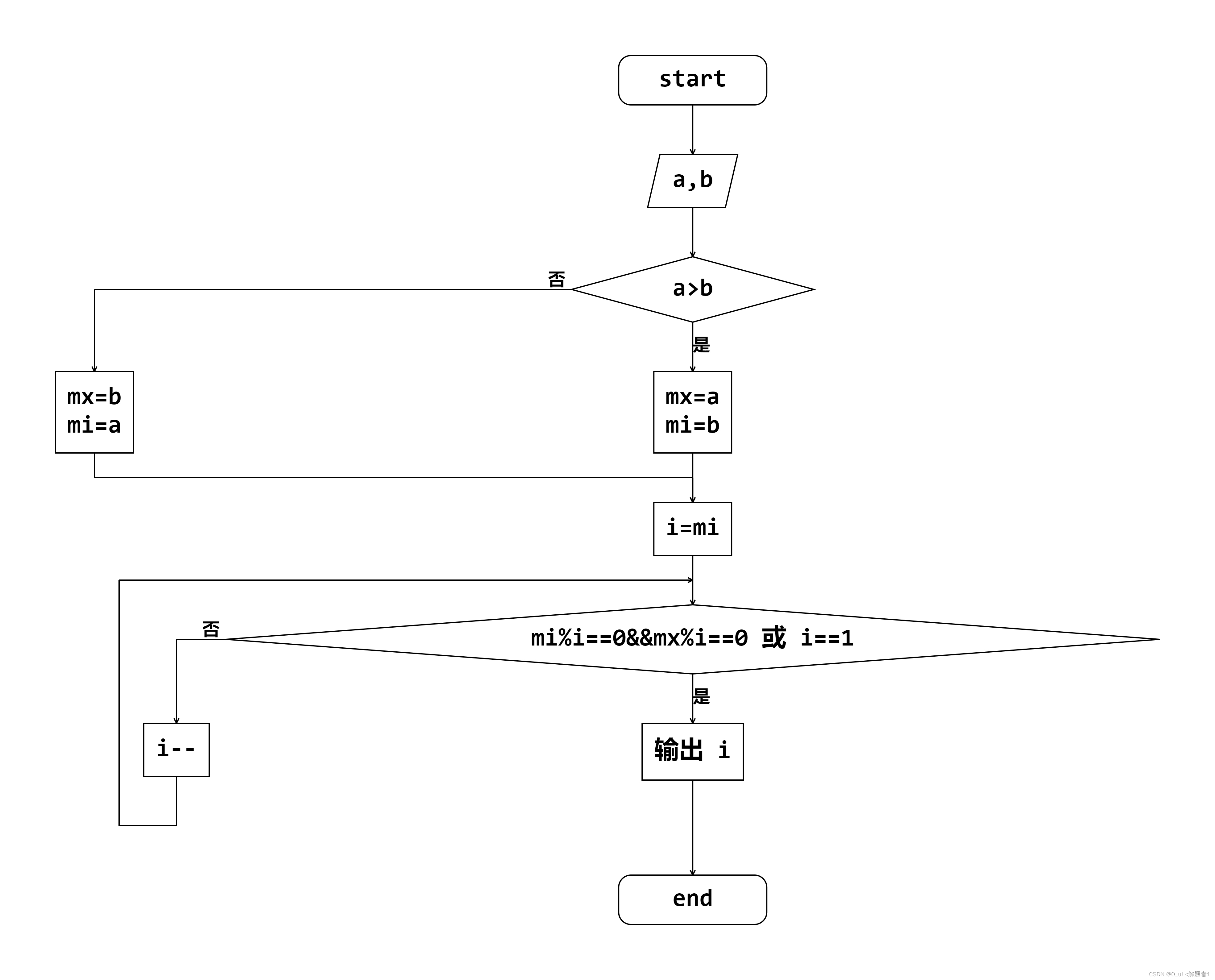
这个算法只经历一次循环,时间复杂度为O(n),貌似还可以,但有人给了我们更优的算法!他们是————
✔🔑🔑🔑🔑🔑🔑🔑🔑🔑🔑🔑🔑🔑🔑🔑🔑解题分割线
2:欧几里得辗转相除法——《几何原本》⋙

[1]辗转相除法公式:gcd(a,b) = gcd(b,a mod b)
实现补充:非零数n与0的最大公约数永远为n
证明如下——
记a为两数中的更大数,b为较小数
1.首先,当b≠0时,记a=kb+r (a,b,k,r均为正整数,且r=a mod b)
2.假设d是a,b的一个公约数,记作d|a,d|b,即a和b都可以被d整除。
而r = a - kb,两边同时除以d,r/d=a/d-kb/d,由等式右边可知m=r/d为整数,因此d|r
3.因此d也是b,a mod b的公约数。
4.因(a,b)和(b,a mod b)的公约数相等,则其最大公约数也相等,得证gcd(a,b) = gcd(b,a mod b)
示例:
假如需要求 2022 和 507两个正整数的最大公约数,用欧几里得算法,是这样进行的:
2022/507=3 余501
507/501=1 余6
501/6=83 余3
6/3=2 余0
终止:
3和0的最大公约数为3,即2022和507的最大公约数为3
以除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公约数,所以就得出了 2022和 507 的最大公约数 3。
💥对比一下朴素枚举的504步,这里我们只用了4步!
[2]我们可以将辗转相除法表示成如下递归式—— [^1]

[3]这样就很容易:C/C++递归代码实现如下🌀
int gcd(int a, int b) {
return !b ? a : gcd(b, a % b);
}
- 这个!是取非的意思,当b为0,!b为真;
- %是取模的意思,对应数学的mod
- 辗转相除法的时间复杂度为O(log2 n)
[4]:next:C/C++非递归代码实现如下🌀
int gcd(int a,int b){
int tmp;
a=max(a,b);
b=min(a,b);//题目已知a为较大数,这里再强调一下
while(b!=0){
tmp=a%b;
a=b;
b=tmp;
}
return a;
}
[5]辗转相除法:流程图😈:
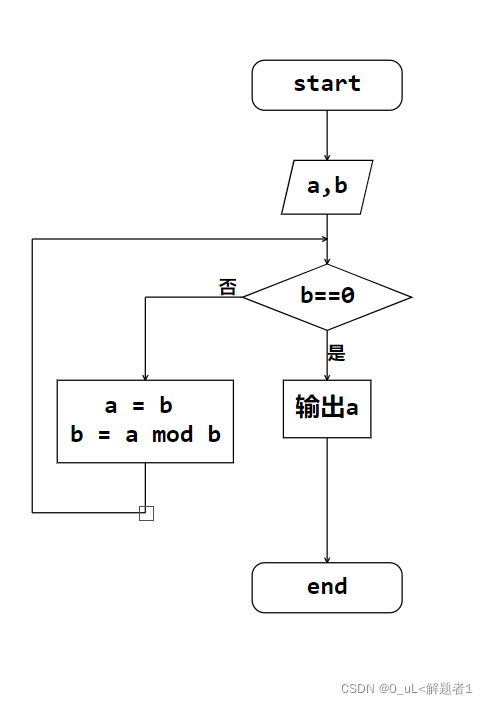
10100001000111000101001000101000100111111**【01分割线】**
3:中国古代:更相减损术——《九章算术》⋙

[1]什么是更相减损法
原文:
可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。
更相减损术,即:
- 任意给定两个正整数,判断它们是否都是偶数
如果是,则都用2约简;若不是,则进行第二步 - 用较大数减较小数,接着把所得的差与较小数比较,继续以大数减小数
重复第二步,直到所得的差与减数相等 - 将第二步最终结果乘上第一步所约去的2,即为这两个整数的最大公约数
转化为公式:
gcd(a,b)=gcd(b,a-b),a>b
gcd(a,b)=gcd(a,b-a),a<b
gcd(a,b)=a, a=b
证明如下——
设gcd(x,y)=d,则满足x=k1* d,y=k2* d,易得k1与k2互质。
情况1:x=y。显然,gcd(x,y)=x=gcd(x,0)=gcd(x,y-x)。
情况2:设x<y
用反证法。
假设k1,(k2 - k1)不互质,
令gcb(k1,k2-k1) = m(m为正整数且m>1);
k1 = m* a,k2 - k1 = m* b
k2 = (a+b)m
即k1,k2有公约数m,与k1,k2互质矛盾
所以假设不成立
即k1,(k2 - k1)互质
所以gcb(x,x-y) = d = gcb(x,y)
综上,gcd(x,y)=gcd(x,y-x)。
命题得证.
补充:若两数无公约数,则称这两数互质
[2]you递归式推得:C/C++递归代码实现如下🌀
int gcd(int a,int b){
if(a%2==0&&b%2==0)return 2*gcd(a/2,b/2);
if(a==b)return a;
else if(a>b)return gcd(b,a-b);
else if(a<b)return gcd(a,b-a);
}
[3]更相减损术next:非递归代码实现如下🌀
int gcd(int a,int b){
int cnt=0;
while(a%2==0&&b%2==0){
a/=2;
b/=2;
cnt++;
}
while(a!=b){
if(a>b)a-=b;
else b-=a;
}
for(int i=0;i<cnt;i++)a*=2;
return a;
}
[4]更相减损数:流程图😈:
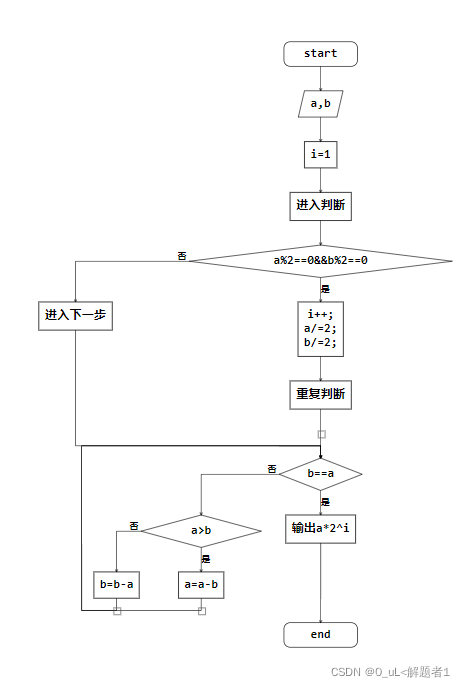
4.J.stein的stein算法
[1]stein算法【探秘】《
Stein算法只有整数的移位和加减法,很好地弥补了辗转相除法
在大质数处理上的缺陷,是对更相减损术
的进一步大补充
递推式:
1 . gcd(a,b)=2*gcd(a/2,b/2), a mod 2=0且b mod 2=0时
2. gcd(a,b)=gcd(a/2,b), a mod 2=0且b mod 2≠0时
3. gcd(a,b)=gcd(a,b/2), a mod 2≠0且b mod 2=0时
接着:就是更相减损数
gcd(a,b)=gcd(b,a-b),a>b
gcd(a,b)=gcd(a,b-a),a<b
gcd(a,b)=a, a=b
1、可以发现,stein算法在更相减损数前置的判断过程中进一步做了简化。
2、它的思路也很简单,在更相减损术的判断过程中,如果其中一个为奇数,另一个为偶数,那么它们绝对不含有公约数2️⃣,因此我们可以将那个偶数连除以2️⃣,直到为其奇数。
3、这样我们在后面的【更相减损】中的计算就大大简化了
[2]所以:stein递归代码实现如下🌀
int gcd(int a,int b){
if(a<b){
a^=b;
b^=a;
a^=b;//保证较大数在形参列表的最前面,防止减出负数
}
if(a==b)return a;
if((!(a&1))&&(!(b&1)))return gcd(a>>1,b>>1)<<1;
else if((!(a&1))&&(b&1))return gcd(a>>1,b);
else if((a&1)&&(!(b&1)))return gcd(a,b>>1);
else return gcd(a-b,b);
}
[3]关于位运算方面的补充:
- 对正整数n而言,n>>1等价n/2
- n<<1等价n*2
- n&1等价n%2
- 这种操作叫位运算,比*/%快很多,
- 详细可见👇
《位运算详解》
stein算法:C/C++非递归代码实现如下🌀
int gcd(int a,int b){
int k=1;
while((!(a&1))&&(!(b&1))){
k<<=1; //用k记录全部公因子2的乘积 ;
a>>=1;
b>>=1;
}
while(!(a&1))a>>=1;
while(!(b&1))b>>=1;
if(a<b) a^=b,b^=a,a^=b; //交换,使a为较大数;
while(a!=b){
a-=b;
if(a<b){
a^=b;
b^=a;
a^=b; //交换,使a为较大数;
}
}
return k*a;
}
总结⋙
GCD问题和LCM问题,是最最经典的数论问题,不仅要熟用模板,更要熟练其背后的推导、证明过程,这对以后的算法学习大有帮助/
终于把GCD问题解透了🐉!
🐱🏍🔑真是不容易。
算法学习之路总是布满了曲折,有时一个简单的问题也能困扰人好久,但是那份成长与突破的喜悦是不言而喻的。💖
这就是解题的奥妙了。






















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










