记录结果再利用的“动态规划”

最新推荐文章于 2022-05-12 14:57:34 发布

kiligsmile

最新推荐文章于 2022-05-12 14:57:34 发布

阅读量410

点赞数 4

分类专栏：算法文章标签：动态规划算法蓝桥杯 c++ acm竞赛

本文链接：https://blog.csdn.net/weixin_62526435/article/details/121747795

版权

算法专栏收录该内容

11 篇文章 2 订阅

订阅专栏

持续更新中😬 加个关注，后续上新不错过~

动态规划算法设计的步骤：

分析最优解的结构
递归定义最优解

自底向上或自顶向下计算最优值
根据最优值得到的信息构造问题的最优解

一、背包问题

问题描述：

有n个重量和价值分别为wi,vi的物品。从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中价值总和的最大值。

限制条件

1≤n≤100
1≤wi,vi≤100

1≤W≤10000

输入：

n=4

(w,v) = {(2,3),(1,2),(3,4),(2,2)}

W=5

输出：

7（选择0、1、3号物品）

方法一：暴力求解

分析：

采用暴力法直接求解，这种方法的搜索深度为n，而且每一层的搜索都需要两次分支，最坏就需要O(2n)的时间，会超时。

参考代码：

#include <iostream>
#include<cstring>
using namespace std;
#define MAX 101
int n,i,weight;
int w[MAX],v[MAX];
int rec(int i,int j)
{
    int res;
    if(i==n){
        res=0;
    }
    else if(j<w[i]){
        res=rec(i+1,j);
    }
    else{
        res=max(rec(i+1,j-w[i])+v[i],rec(i+1,j));
    }
    return res;
}
int main()
{
    scanf("%d",&n);
    for(i=0;i<n;i++){
        scanf("%d%d",&w[i],&v[i]);
    }
    scanf("%d",&weight);
    printf("价值总和最大为：%d\n",rec(0,weight));
    return 0;
}

方法二：记忆化搜索

通过针对样例输入的情形下rec递归调用的情况，可以发现rec以(3，2)为参数调用了两次，如果参数相同，返回的结果也应该相同，于是第二次调用时已经知道了结果却白白浪费了计算时间，可以第一次计算时的结果记录下来、这样就可以减少重复计算。

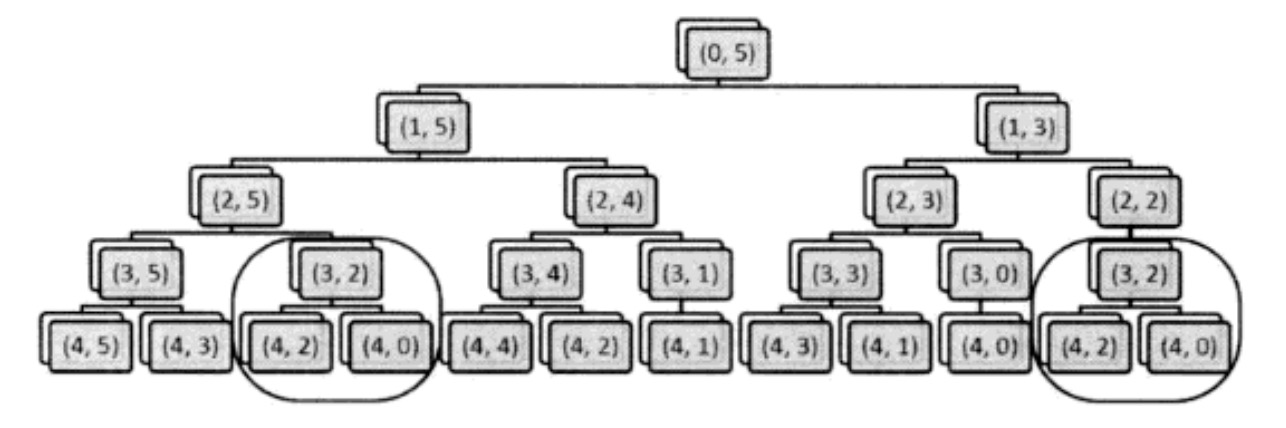
分析：

这微小的改进能降低多少复杂度呢?对于同样的参数，只会在第一次被调用时执行递归部分，第二次之后都会直接返回。参数的组合不超过nW中，而函数内只调用两次递归，所以只需要O(nW)的复杂度就能解决这个问题

参考代码：

#include <iostream>
#include<cstring>
using namespace std;
#define MAX 101
int n,i,weight;
int w[MAX],v[MAX];
int dp[MAX][MAX];
int rec(int i,int j)
{
    if(dp[i][j]>=0){
        return dp[i][j];
    }
    int res;
    if(i==n){
        res=0;
    }
    else if(j<w[i]){
        res=rec(i+1,j);
    }
    else{
        res=max(rec(i+1,j-w[i])+v[i],rec(i+1,j));
    }
    return dp[i][j]=res;
}
int main()
{
    scanf("%d",&n);
    for(i=0;i<n;i++){
        scanf("%d%d",&w[i],&v[i]);
    }
    scanf("%d",&weight);
    memset(dp,-1,sizeof(dp));
    printf("价值总和最大为：%d\n",rec(0,weight));
    return 0;
}

方法三：动态规划法

接下来，我们来仔细研究一下前面的算法利用到的这个记忆化数组。记dp[i][j]为根据rec的定义，从第i个物品开始挑选总重小于j时，总价值的最大值。于是我们有如下递推式：

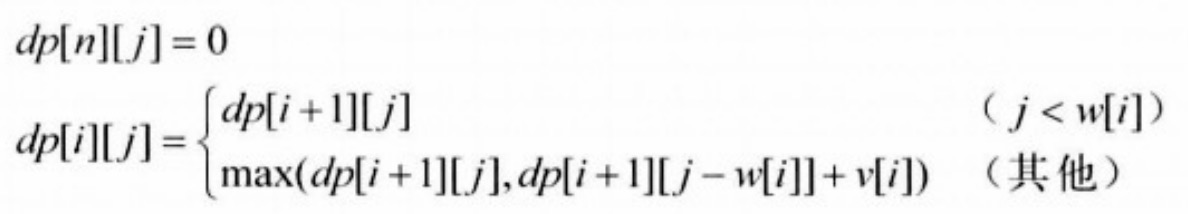
如上所示，不用写递归函数，直接利用函数递推式将各项的值计算出来，简单地用二重循环也可以解决这一问题

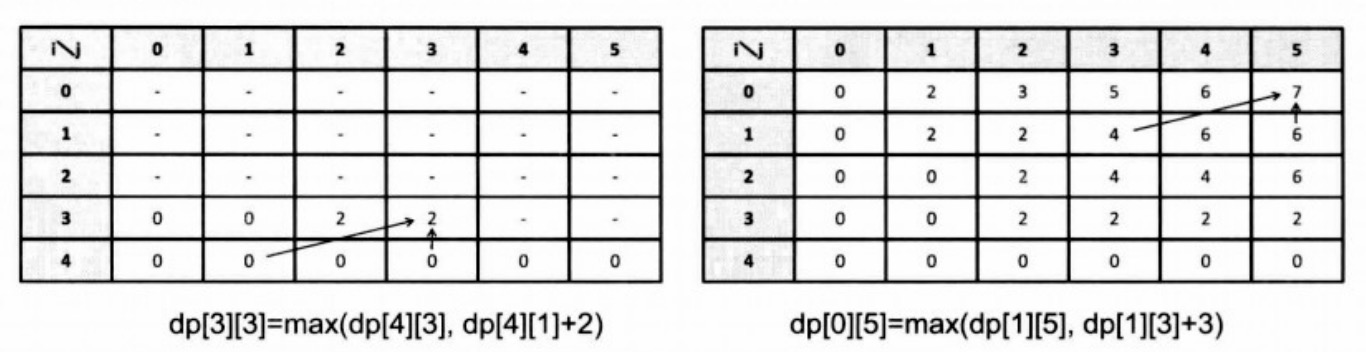
参考代码：

#include <iostream>
#include<cstring>
using namespace std;
#define MAX 101
int n,i,j,weight;
int w[MAX],v[MAX];
int dp[MAX][MAX];
int main()
{
    scanf("%d",&n);
    for(i=0;i<n;i++){
        scanf("%d%d",&w[i],&v[i]);
    }
    scanf("%d",&weight);
    memset(dp,0,sizeof(dp));
    for(i=n-1;i>=0;i--){
        for(j=0;j<=weight;j++){
            if(j<w[i]){
                dp[i][j]=dp[i+1][j];
            }
            else{
                dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);
            }
        }
    }
    printf("价值总和最大为：%d\n",dp[0][weight]);
    return 0;
}

分析：

这个算法的复杂度与前面相同，也是O(nW)，但是简洁了很多。以这种方式一步步按顺序求出问题的解的方法被称作动态规划，也就是常说的DP。解决问题时，即可以按照如上方法从记忆化搜索出发推导出递推式，熟练后也可以直接得出递推式。记得数组的初始化

输出结果：

二、最长公共子序列问题（LCS)

问题描述：

限制条件：

1≤n,m≤1000

输入：

n=4

m=4

s="abcd"

t="becd"

输出：

3（"bcd")

辨析最长公共子序列和最长公共子串：

最长公共子序列：

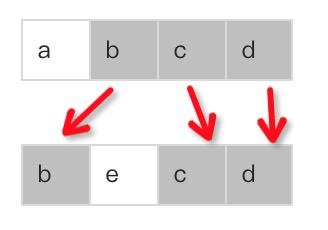
最长公共子串

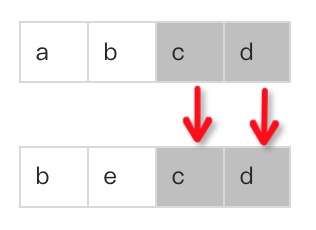
分析：

定义dp[i][j]:=s1...sj和t1...tj对应的LCS的长度

由此，s1...si+1和t1...tj+1对应的公共子列可能是：

当si+1=tj+1时，在s1...sj和t1...tj公共子列末尾追加上si+1
s1...si和t1...tj+1和的公共子列

s1...si+1和t1...tj的公共子列

三者中的某一个，所以就有如下的递推关系成立：

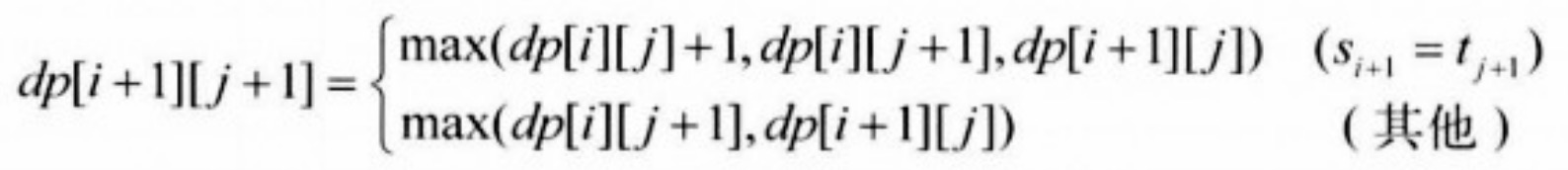
这个递推式可用O(nm)计算出来，dp[n][m]就是LCS的长度。

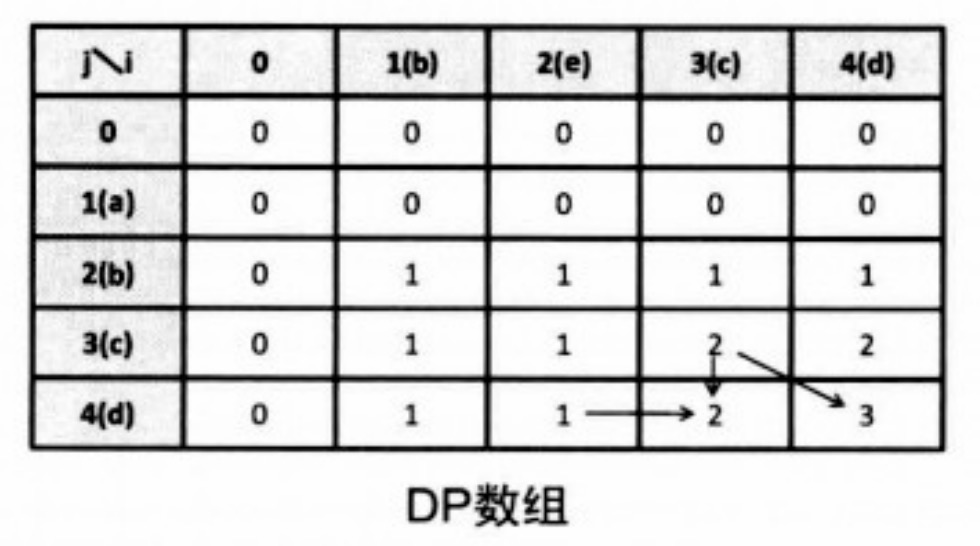
参考代码：

#include <iostream>
using namespace std;
#define N 1000
int m,n;
char s[N],t[N];
int dp[N+1][N+1];
int main()
{
    int i,j;
    scanf("%d%d",&n,&m);
    scanf("%s",s);
    scanf("%s",t);
    for(i=0;i<n;i++){
        for(j=0;j<m;j++){
            if(s[i]==t[j]){
                dp[i+1][j+1]=dp[i][j]+1;
            }
            else{
                dp[i+1][j+1]=max(dp[i][j+1],dp[i+1][j]);
            }
        }
    }
    printf("%d\n",dp[n][m]);
}

输出结果：

三、数塔问题

问题描述：

有形如图中所示的一个灯塔，从顶部出发，在每一结点可以选择向左走或是向右走，一直走到底层，要求找出一条路径，使路径上的数值和最大

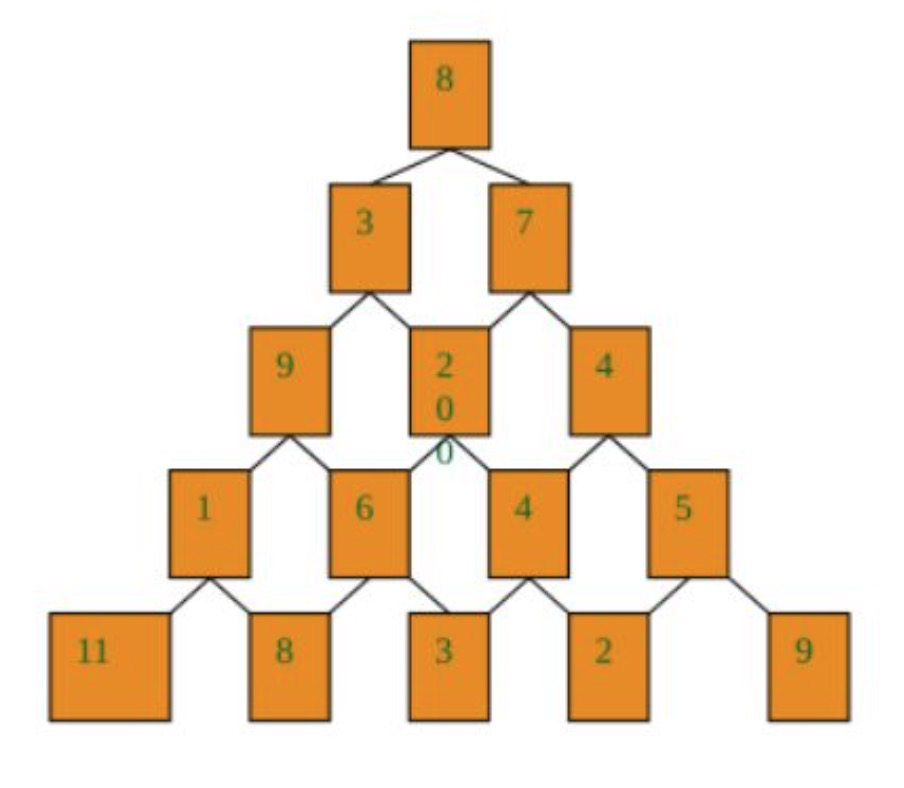
分析：

使用动态规划考虑数塔问题时，可以自底向上找最大路径和，自顶向下找最优路径

上一层的走法，取决于下一层的最优解，举例：

如果经过第三层9，则第三层中1和6肯定选择6，

如果经过第三层2，则第三层中6和4肯定选择6，

如果经过第三层4，则第三层中4和5肯定选择5，

......

经过一次次决策，问题降了一阶，四层数塔问题变成三层数塔问题，如此循环往复，最后得到一层数塔的最优值

首先使用一个二维数组num记录数塔的原始值（下三角矩阵）:

8
3	7
9	20	4
1	6	4	5
11	8	3	2	9

其次，初始化dp，dp的初始值即为num对应的值

递推式为dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1])

本题中，dp数组为：

49
37	41
26	34	18
12	14	7	14
11	8	3	2	9

最后通过

for(i=1;i<n;i++){
    value=dp[i-1][j]-num[i-1][j];
    if(value==dp[i][j+1]){
        j++;
    }
    printf("->%d",num[i][j]);
}

求得最大路径和对应的路径

参考代码：

#include <iostream>
using namespace std;
#define N 50
int num[N][N];
int dp[N][N];
int n,i,j;

void countdp()
{
    int value;
    for(i=n-1;i>=0;i--){
        for(j=0;j<=i;j++){
            dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1]);
        }
    }
    j=0;
    printf("最大路径和：%d\n",dp[0][0]);
    printf("最大路径：%d",num[0][0]);
    for(i=1;i<n;i++){
        value=dp[i-1][j]-num[i-1][j];
        if(value==dp[i][j+1]){
            j++;
        }
        printf("->%d",num[i][j]);
    }
    printf("\n");
}

int main()
{
    printf("请输入灯塔的层数：\n");
    scanf("%d",&n);
    printf("请依次输入各层上的数据：\n");
    for(i=0;i<n;i++){
        for(j=0;j<=i;j++){
            scanf("%d",&num[i][j]);
            dp[i][j]=num[i][j]; 
        }
    }
    countdp();
}

输入输出样例：

四、最短路问题

问题描述：

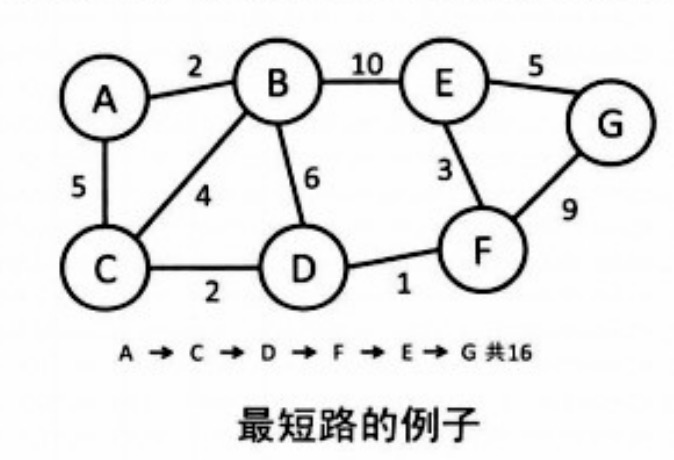
最短路问题是图论中最基础的问题，在程序设计竞赛试题中也经常出现。最短路是给定两个顶点，在以这两个点为起点和终点的路径中，边的权值和最小的路径。如果把权值当做距离，考虑最短距离的话就很容易理解了，智力游戏中的求解最少步数问题也可以说是一种最短路问题。

举例：

一、单源最短路问题1（Bellman-Ford)算法（只适用于给定图为DAG)

分析：

单源最短路问题是固定一个起点，求它到其他所有点的最短路的问题。终点也固定的问题叫做两点之间最短路问题。但是因为解决单源最短路问题的复杂度也是一样的，因此通常当做单源最短路问题来求解

记从起点s出发到顶点i的最短距离为d[i]。则下述等式成立。

d[i]=min{d[j]+(从j到i的边的权值)|e=(j,i)∈E}

如果给定的图是一个DAG(没有圈的有向图)，就可以按拓扑序给顶点编号，并利用这条递推关系式计算出d。但是，如果图中有圈，就无法依赖这样的顺序进行计算。在这种情况下，记当前到顶点i的最短路长度为d[i],并设初值d[s]=0,d[i]=INF(足够大的常数)，再不断使用这条递推关系式更新d的值，就可以算出新的d。只要图中不存在负圈，这样的更新操作就是有限的。结束之后的d就是所求的最短距离了。

举例：

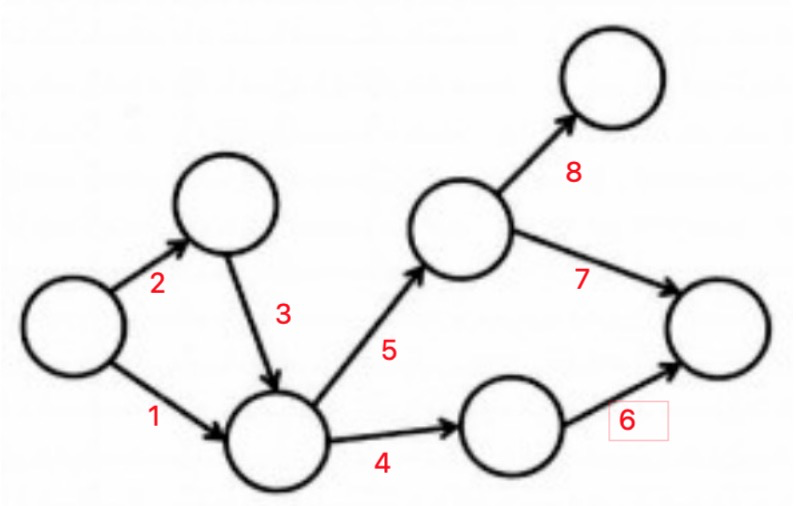
步骤：

对于每一个顶点我们给它一个编号，第i号顶点叫做Vi

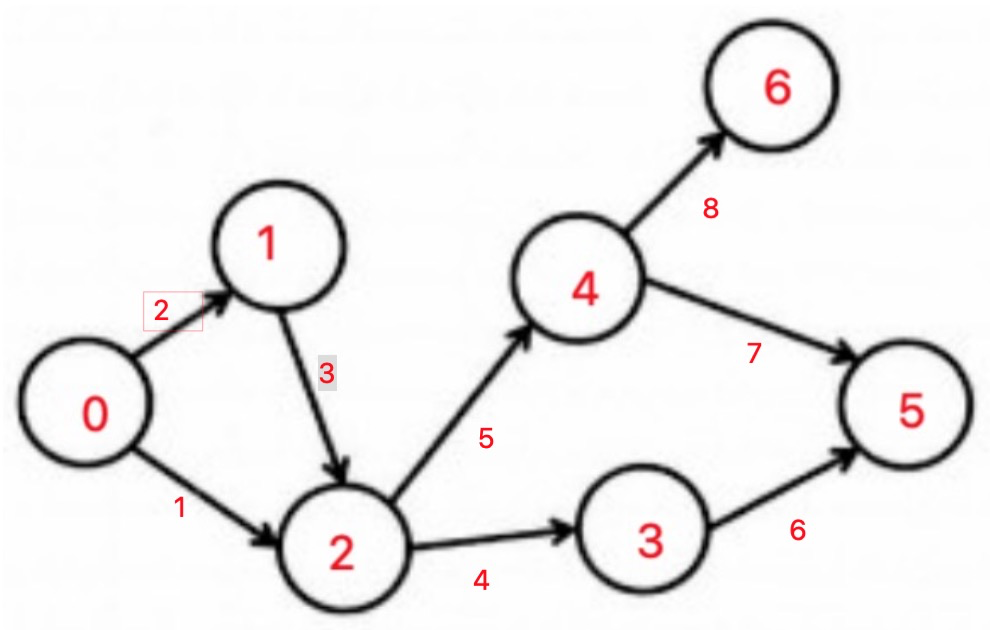
那么存在从顶点到顶点的边时就有i<j成立，这样的编号方式叫做拓拓扑序

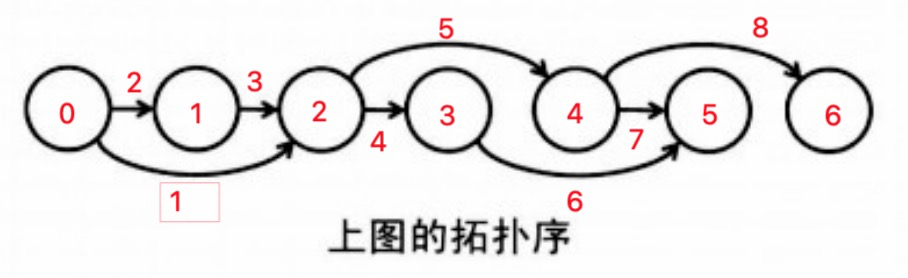
如果把图中的顶点按照拓扑序从左到右排列，那么所有的边都是从左指向右的。因此，通过这样的编号方式，有些DAG问题就可以使用DP来解决了。求解拓扑序的算法叫做拓扑排序

参考代码：

#include <iostream>
using namespace std;
#define max_E 50
#define INF 1000000
struct edge {int from,to,cost;}; // 从顶点from指向顶点to的权值为cost的边
edge es[max_E]; //边
int d[max_E];  // 最短距离
int V,E;  // V是顶点数，E是边数

// 求解从顶点s出发到所有点的最短距离
void shortest_path(int s)
{
    int i;
    for(i=0;i<V;i++){
        d[i]=INF;
    }
    d[s]=0;
    while(true){
        bool update = false;
        for(i=0;i<E;i++){
            edge e =es[i];
            if(d[e.from]!=INF&&d[e.to]>d[e.from]+e.cost){
                d[e.to]=d[e.from]+e.cost;
                update=true;
            }
        }
        if(!update){
            break;
        }
    }
}
int main()
{
    int s,i;
    printf("请输入顶点数：");
    scanf("%d",&V);
    printf("请输入边数：");
    scanf("%d",&E);
    printf("请依次输入各边的起点、终端，以及两点之间的距离：\n");
    for(i=0;i<E;i++){
        scanf("%d%d%d",&es[i].from,&es[i].to,&es[i].cost);
    }
    printf("请输入起点：");
    scanf("%d",&s);
    shortest_path(s);
    for(i=0;i<V;i++){
        printf("%d->%d的最短距离为：%d\n",s,i,d[i]);
    } // 若最终输出结果≥INF则说明两点之间没有通路
}

输入输出样例：

如果在图中不存在从s可达的的负圈,那么最短路不会经过同一个顶点两次(也就是说，最多通过 |V|-1 条边), while(true)的循环最多执行|V|-1次，因此，复杂度是O(|V|x|E|)。反之，如果存在从s可达的负圈，那么在第|V|次循环中也会更新d的值，因此也可以用这个性质来检查负圈。如果-开始对所有的顶点i，都把d[i]初始化为0,那么可以检查出所有的负圈。

负圈又称负环，就是说一个全部由负权的边组成的环，这样的话不存在最短路，因为每在环中转一圈路径总长就会变小。

// 若返回true，则存在负圈
bool find_negative_loop()
{
    int i,j;
    memset(d,0,sizeof(d));
    for(i=0;i<V;i++){
        for(j=0;j<E;j++){
            edge e = es[j];
            if(d[e.to]>d[e.from]+e.cost){
                d[e.to]=d[e.from]+e.cost;
                if(i==V-1){
                    return true; // 如果第V次仍然更新了，则存在负圈
                }
            }
        }
        
    }
    return false;
}

若有帮助的话，请点个赞吧！😊