吃水果——组合、动态规划_分小朋友苹果对半分动态规划-CSDN博客

本文链接：https://blog.csdn.net/weixin_63001635/article/details/137648328

文章介绍了如何使用动态规划解决一个关于n个小朋友分配水果的问题，确保恰好有k个小朋友的水果与左边的不相同。通过组合数和快速幂的计算，给出了Java代码实现，展示了状态表示、状态计算过程以及最终的解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

思路

组合

题目要求n个小朋友中恰好有k个小朋友拿到的水果和左边的不一样，那说明另外n-k-1（除去k个和最左边的那个）个小朋友的水果要和左边的相同。

我们可以用 $C_{n-1}^k$ 来将n个小朋友划分k+1个部分。（即在n-1个空隙中插k个隔板分成k+1个部分）
每个部分小朋友选择的水果相同，第 i 组小朋友选择的水果和第 i-1 组的不相同。（i>1）

我们选择2~k 部分的最左边的小朋友（第一部分不算入k个里面）即选择了k个小朋友，可以保证，这个每个部分最左边的小朋友和前一个小朋友选择的水果不同，因此，我们找出了其中恰好有k个小朋友和左边相邻的小朋友水果不同。

用 $C_{n-1}^k$ 满足第一点， $m*(m-1)^k$ 满足第二点，其中 m 表示第一部分小朋友可以随意选择，其余部分不能选择与前一个相同的水果，即 $m-1$ 种，一共选 $k$ 次。

因此，故总共有 $C_{n-1}^k*(m)*(m-1)^k$ 种选法。

计算组合：递推存在公式 $C_i^j = C_{i-1}^j+C_{i-1}^{j-1}$

计算幂次方：快速幂快速幂（求解原理+例题）-CSDN博客

代码（java）

import java.util.*;

class Main{
    static int N = 2010 , mod = 998244353;
    static int n,m,k;
    static long[][] c = new long[N][N];
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        k = in.nextInt();
        long res = m; // m
        res = res*C(n-1,k)%mod; // C(n-1,k)
        res  = res*qmi(m-1,k,mod)%mod; // (m-1)^k
        System.out.print(res);
    }
    // 快速幂
    public static long qmi(long a,long k,long b){
        long res = 1;
        while(k!=0){
            if((k&1)==1){
                res = res*a%b;
            }
            a = a*a%b;
            k = k>>1;
        }
        return res;
    }
    // 递推 c[i][j] = c[i-1][j]+c[i-1][j-1]
    public static long C(int n,int k){
        for(int i=0;i<=n;i++){
            for(int j=0;j<=i;j++){
                if(j==0) c[i][j] = 1;
                else c[i][j] = (c[i-1][j]+c[i-1][j-1])%mod;
            }
        }
        return c[n][k];
    }
}

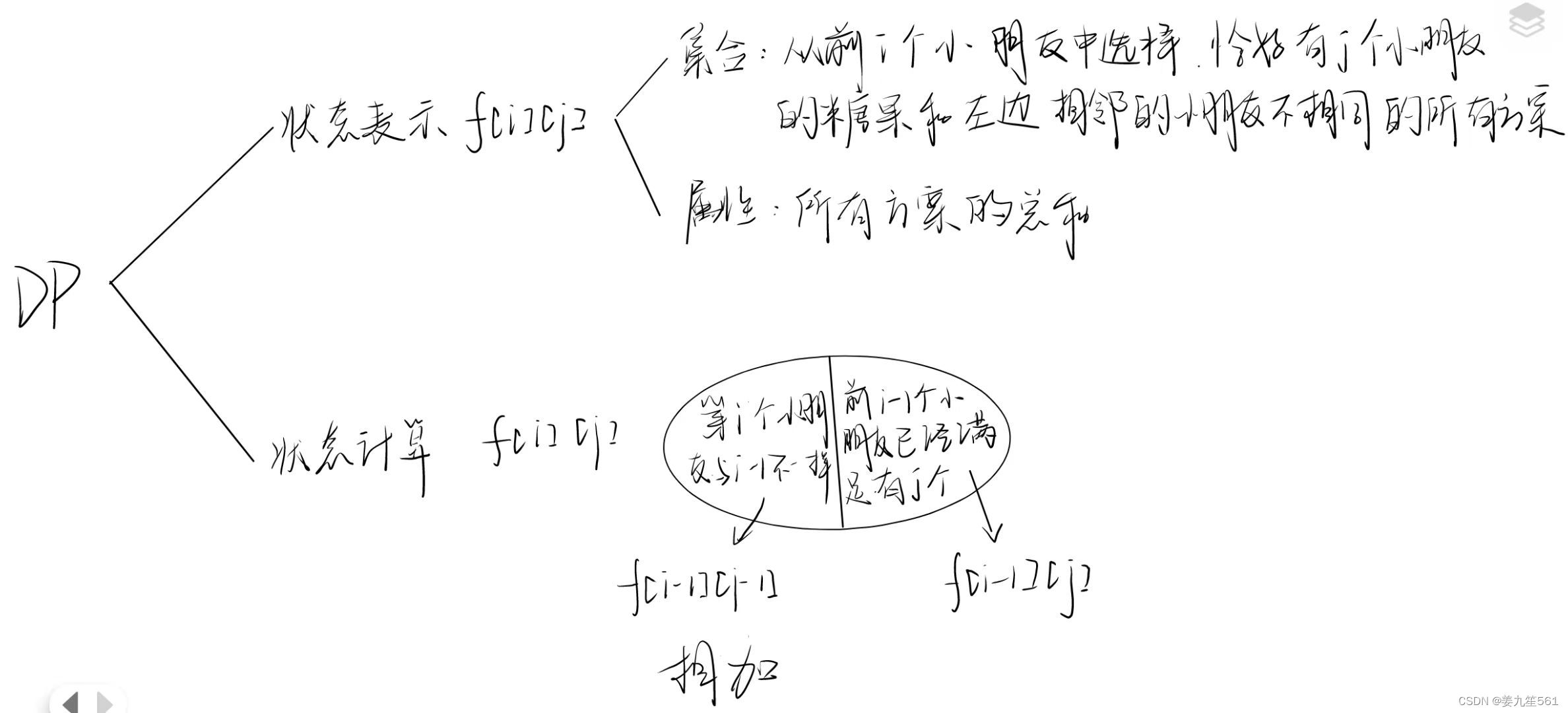
DP

状态表示： $f[i][j]$

集合：从前 i 个小朋友中选择，恰好有 j 个小朋友的水果和左边相邻的小朋友的水果不相同的所有方案。

属性：所有方案的和

状态计算：

第 i 个小朋友的糖果和第 i-1 不相同 $f[i][j] += f[i-1][j-1]$
前 i-1 个小朋友已经满足有 j 个不相同的 $f[i][j] += f[i-1][j]$

代码（java）

import java.util.*;

class Main{
    static int n,m,k,res;
    static final int mod = 998244353;
    static long[][] f = new long[2010][2010];
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        k = in.nextInt();
        for(int i=1;i<=n;i++) f[i][0] = m; //f[i][0]=m的定义是前i个同学拿完以后，恰有0个同学和左边的同学不一样，也就是所有同学都相等,有m种水果，即m种方案
        for(int i=2;i<=n;i++){
            for(int j=1;j<=k;j++){
                f[i][j] = (f[i-1][j]+f[i-1][j-1]*(m-1)%mod)%mod; // 乘以(m-1)是在以前的基础上，第i个可以选m-1种，乘上就是所有的方案
            }
        }
        System.out.println(f[n][k]);
    }
    
}