【数字信号处理】第三章 离散傅里叶变换DFT及FFT快速算法

---

前言

这里其实是整个数字信号处理最难的部分了, 大多数同学在这里栽跟头, 主要还是新概念.
在高中的时候面对新概念, 也烦, 但不至于到怕.
为什么现在怕了? 主要还是时间不够, 太快了. 这不, 半个学期过去马上就要迎来考试, 匆匆忙忙写下这篇, 希望能给自己和大家带来帮助.

记住, 考试只是辅助监督, 知识有没有学到是你自己的.

---

1 DFT定义和物理意义

N为采样点数, 也称为DFT的区间长度, 要求N≥序列长度

1.1 DFT \ ZT \ DTFT之间的关系

结论:

1. 序列x(n)的傅里叶变换X(ejw)是序列的Z变换X(z)在单位圆上的取值。
2. 序列x(n)的N点DFT变换X(k)是序列傅里叶变换X(ejw)在频率区间[0，2pi]上的N点等间隔采样，采样间隔为
   2pi /N。
3. 序列的N点DFT变换X(k)是序列的Z变换X()在单位圆上的N点等间隔采样，频率采样间隔为2pi /N
   
   这道立体里,
   求和长度n和采样点数N一样的时候, k!=0时等于0! 对称相减了!
   等比数列求和公式

---

2 DFT性质

1. 线性性质

2. 隐含周期性: X(k)采样点数N为周期 $X(k)=X(k+mN)和x(n)=x(n+mN)$

3. 循环移位性质: $y(n)=x((n+m){)}_N\cdot R_N(n)$
   具体顺序为, 先以N为周期延拓, 然后移位m个单位, 取0~N-1为主值

4. 时域的循环移位性质: 假如 $y(n)=x((n+m){)}_N\cdot R_N(n)$则
   $Y(k)=X(k)W_N^{-km}$

5. 频域的循环移位性质: 假如$Y(k)=X((k+l){)}_N{R}_N(k)$ 则
   $y(n)=x(n)W_N^{nl}$

6. 复共轭序列$x^{\ast }(n)的DFT为X^{\ast }(N-k)和x^{\ast }(N-n)的DFT为X^{\ast }(k)$
   N为序列的长度

7. 圆周共轭对称序列 $x_{ep}(n)$ 满足
   $$x_{ep}(n)=x_{ep}^{\ast }(N-n),0\le n\le N-1$$
   圆周共轭反对称序列 $x_{op}(n)$ 满足
   $$x_{op}(n)=-x_{op}^{\ast }(N-n),0\le n\le N-1$$
   任意有限长离散时间序列 $x(n)$ 可以分解成
   $$\begin{array}{rl}& x(n)=x_{ep}(n)+x_{op}(n)0\le n\le N-1\\ & \{\begin{array}{l}{x}_{ep}(n)=\frac{x(n)+x^{\ast }(\mathrm{N}-n)}{2}\\ x_{op}(n)=\frac{x(n)-x^{\ast }(\mathrm{N}-n)}{2}\end{array}\end{array}$$
   

8. 实数序列的对称性
   

9. 循环卷积定理:相当于线性卷积的基础上的移位+取主值
   

---

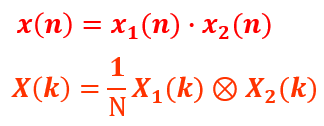
3 频率采样

在分析DFT和ZT关系的时候说道, DFT为在Z平面上单位圆等间隔采样

对DFT反变换得到的$x_N(n)$和原来的$x(n)$有什么关系?

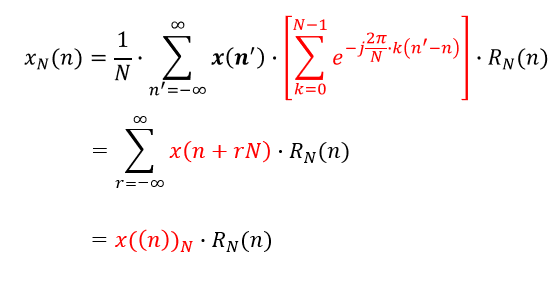
经过推导, 我们可以得到以下结论

$x_N(n)$为--------原来的$x(n)$以N为周期的周期延拓序列的主值序列
主值范围即0~N-1

---

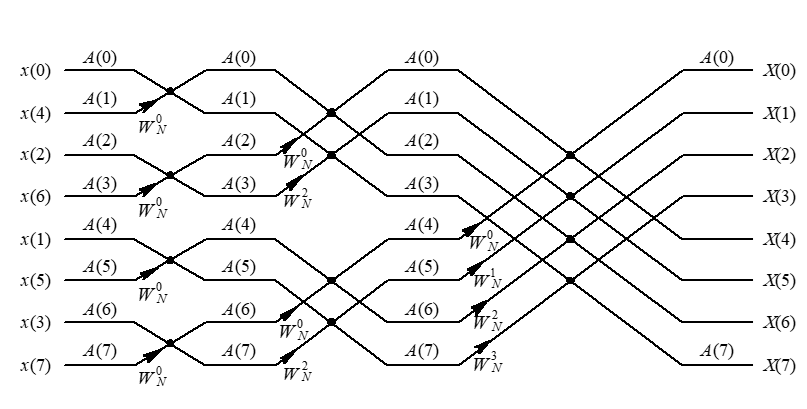
4 DFT的快速算法—FFT

主要是掌握时域-基2的FFT算法和计算DFT和FFT的运算复杂度

• 直接计算DFT的复杂度=$N^2复数乘法+N(N-1)复数加法$
• FFT的复杂度$\frac{N}{2}lo{g}_{2}N复数乘法+Nlo{g}_{2}N复数加法$
  
  

---

5 DFT应用举例

主要是计算离散线性卷积