三重积分的概念，计算（先一后二（投影穿线法））

1.概念：设三元函数f(x,y,z)在可求体积的有界闭域Ω（⊂ R3）上有定义，用分法∆把Ω以任意方式化成n个小区域Ω1，Ω2，...,Ωn,设它们的体积分别为：∆V1,∆V2,...∆Vn,任取一点作和式（称为函数f(x,y,z)在Ω上的积分和）

                              

记d(∆）=max{d(Ω1),d(Ω2),...d(Ωn)}(其中d(Ωk)表示Ωk的直径，显然d(∆)越小，积分和越精确，若极限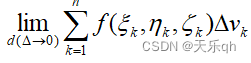

存在，则称函数f(x,y,z)在区域Ω上可积，并且把这个极限值称为函数f(x,y,z)在Ω上的三重积分，记作：

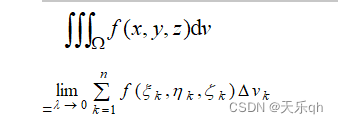
其中：“Ω”称为积分区域，“f（x,y,z）”称为被积函数；“f(x,y,z)dV”称为被积表达式“dV”称为体积微元，直角坐标写作dxdydz；

 

2.三重积分化为累次积分的计算

方法1 .  投影引线法 (“先一后二”)

 

 

 

 

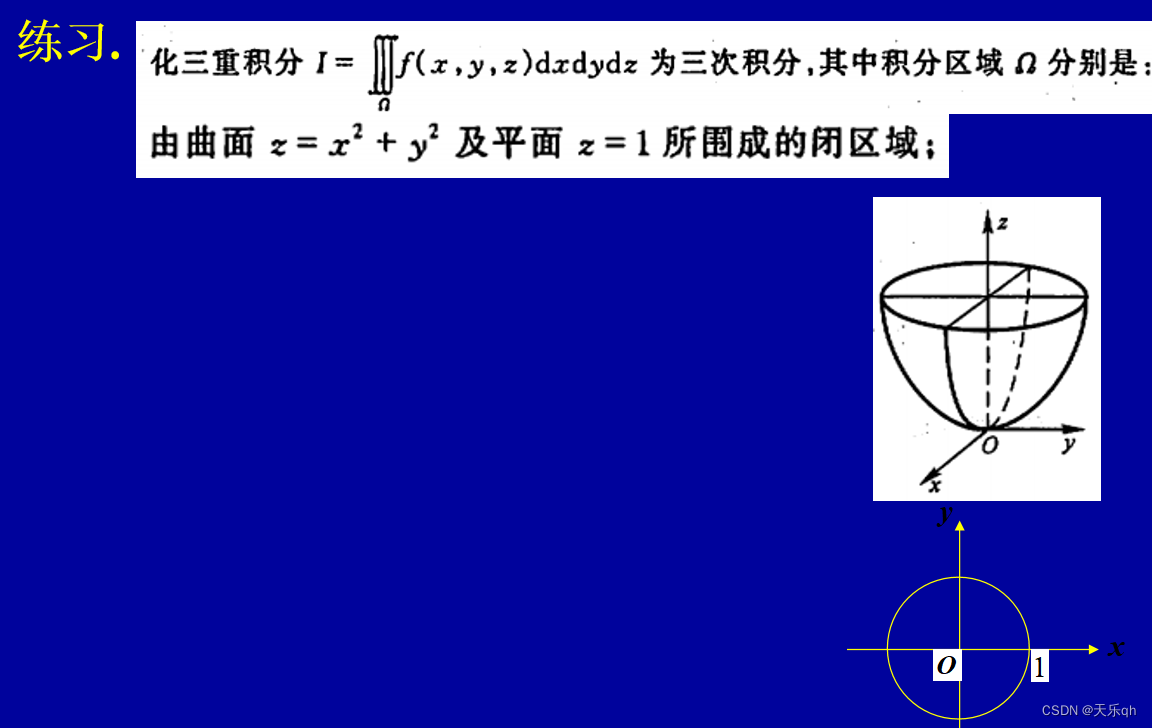
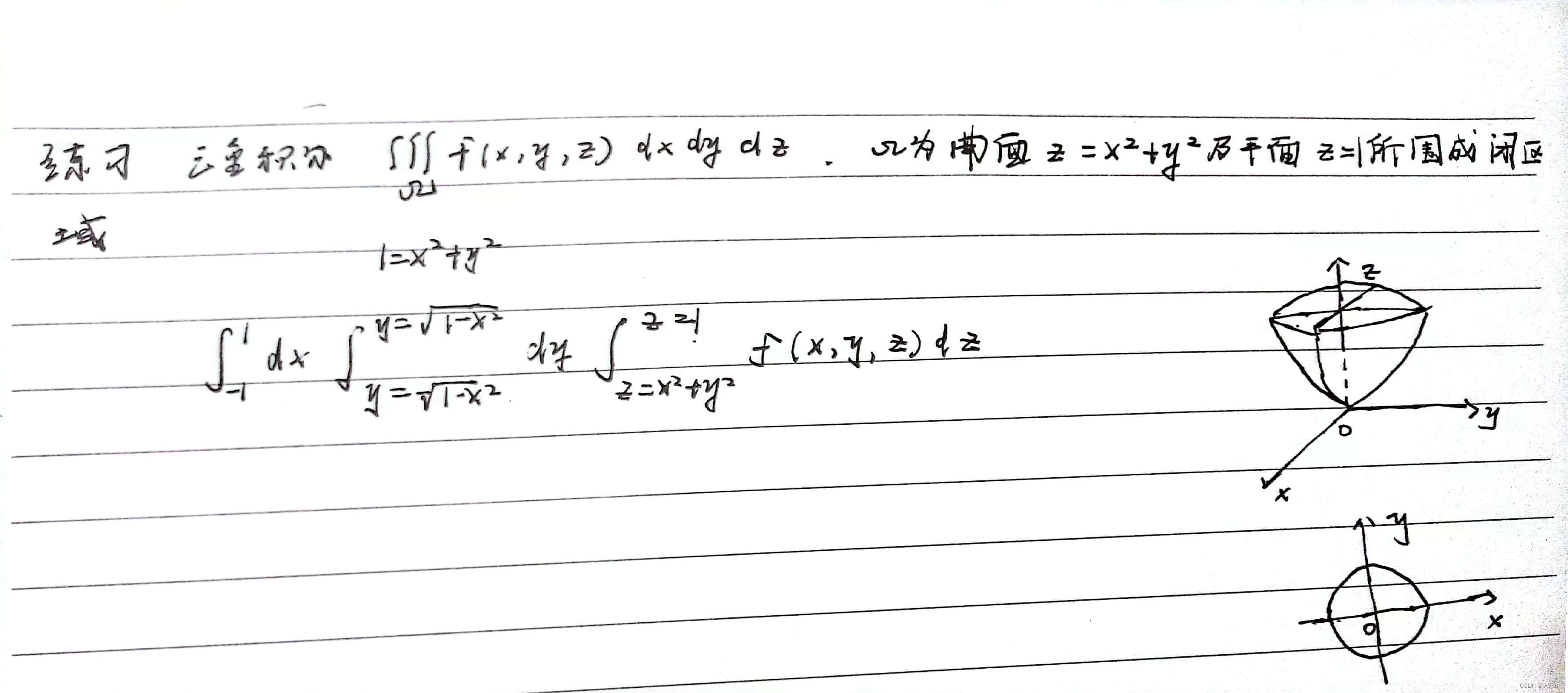
 总结

 方法2 .  截面法 (“先二后一”)  

转自应用高等数学（巢大版）