matlab学习笔记：第三章3.3矩阵的运算(调用函数)

不系之舟71

已于 2024-10-28 10:13:42 修改

阅读量1.1k

点赞数 14

文章标签： matlab 学习笔记

于 2024-10-18 17:21:19 首次发布

本文链接：https://blog.csdn.net/weixin_63883130/article/details/142951509

版权

1.调用函数

(1)常见的数学运算函数

例如abs, sin, round, log等。这些函数可以直接应用到矩阵上，所表示的含义是：对矩阵中的每个元素分别运用这些数学运算函数，因此返回的结果也是一个矩阵。

A = randi(9,3,4)
A1 = mod(A,3)
A2 = floor(A)
A3 = sqrt(A)
A4 = exp(A)
B = rand(3,4)
B1 = round(B,2)
B2 = floor(B)

(2)sum:求和函数

如果A是一个向量，则sum(A)可以计算A中所有元素的和。

如果A是一个矩阵，则sum(A,dim)可以计算A沿维度 dim 中所有元素的和。

dim=1表示沿着行方向，即计算每一列的和。当dim=1时，sum(A,1)可以简写成sum(A)

dim=2表示沿着列方向，即计算每一行的和。

A = 1:10
A1 = sum(A)
B = randi(9,3,4)
B1 = sum(B,1)       %如果dim=1，可以省略
B2 = sum(B,2)
B3 = sum(sum(B))    %先计算B的所有列的和，在计算行向量的和
B3_ = sum(B(:))     %用下标法索引所有的元素生成一个列向量，在计算列向量所有元素的和
B3__ = sum(B,'all') %也是用来计算B的所有元素的和

注意：指定如何处理 NaN 值

NaN（Not a Number）指不定值或缺失值。例如计算0/0 或 0*Inf会返回NaN

默认情况下，如果计算时有一个元素为NaN，那么最终会返回NaN；

我们可以在最后加一个输入参数: 'omitnan', 这样就会忽略NaN

(3)prod:求乘积函数（product）

prod函数的用法和sum函数的用法相同，它是用来计算乘积的。matlab官网手册用法如下：

用法：

B = prod(A)         
B = prod(A,"all")        %B = prod(A,"all") 返回 A 的所有元素的乘积。
B = prod(A,dim)          %B = prod(A,dim) 返回沿维度 dim 的乘积。
                         %例如，如果 A 为矩阵，则 prod(A,2) 为一个包含每一行乘积的列向量。
B = prod(A,vecdim)       %B = prod(A,vecdim) 根据向量 vecdim 中指定的维度返回乘积。例如，如果 A 
                         %是矩阵，则 prod(A,[1 2]) 返回 A 中所有元素的乘积，
                         %因为矩阵的每个元素包含在由维度 1 和 2 定义的数组切片中。
B = prod(___,outtype)    %使用上述语法中的任何输入参量按 outtype 指定的类返回数组。
                         %outtype 可以是 "double"、"native" 或 "default"
B = prod(___,nanflag)    %指定包含还是省略 A 中的 NaN 值。例如，prod(A,"omitnan") 
                         %在计算乘积时会忽略 NaN 值。默认情况下，prod 包括 NaN 值。

A = 1:9
A1 = prod(A)        %计算9！
B = randi(9,3,4)    %创建一个最大值为9的随机整数矩阵
B1 = prod(B,1)      %计算每一列的乘积，1可以省略
B2 = prod(B,2)      %计算每一行的乘积
C = [2,4,NaN,1,10]
C1 = prod(C,"omitnan")  %忽略缺失值
D = [5 3 -8   4;
    1 5 NaN 10;
    3 6 18  9]
D1 = prod(D,"omitmissing")  %计算D每列的乘积，忽略缺失值

(4)cumsum:计算累积和（cumulative sum）

如果A是一个向量，则cumsum(A)可以计算向量A的累积和（累加值）。

如果A是一个矩阵，则cumsum(A,dim)可以计算A沿维度 dim 中所有元素的累积和，具体的使用方法和sum函数类似。也可以在最后加一个输入参数: 'omitnan', 这样计算时会忽略NaN。

用法：

B = cumsum(A)
B = cumsum(A,dim)            %返回沿维度 dim 的元素的累积和。例如，如果 A 是矩阵，则 cumsum(A,2) 沿 A 的各行返回累积和。
B = cumsum(___,direction)    %可在上述任一语法的基础上指定计算方向。例如，umsum(A,2,"reverse"通过从尾到头计算 A 的第二个维度返回其中各行的累积和
B = cumsum(___,nanflag)      %指定包含还是省略 A 中的 NaN 值。例如，cumsum(A,"omitnan")在计算每个和时忽略 NaN 值。默认情况下，cumsum 包括 NaN 值

A = 1:10
A1 = cumsum(A)  %计算结果 1     3     6    10    15    21    28    36    45    55
A2 = sum(A)     %计算结果 55
B = randi(9,4,5)
B1 = cumsum(B,1)    %计算每列累计和
B2 = cumsum(B,2)    %计算每行累计和
C = [5 3 -8   4
    1 5 NaN 10; 
    3 6 18  9]
C1 = cumsum(C,'omitmissing')    %计算c矩阵每列累计和，忽略缺失值

(5)diff:计算差分（difference）

差分运算在和时间相关的数据中用的比较多。在原始序列中用下一个数值减去上一个数值可以得到一个新的序列，这个过程就是一阶差分；在一阶差分结果的基础上再进行一次一阶差分，就是二阶差分，MATLAB中计算差分的函数是diff，我们可以使用diff(A,n)命令计算向量A的n阶差分，当n等于1时，可以直接写成diff(A)。

diff函数也可以用在矩阵上面：diff(A,n,dim)表示沿矩阵A的维度dim方向上计算差分，当dim=1时沿着行方向计算，即得到每列的n阶差分；当dim=2时沿着列方向计算，即得到每行的n阶差分。类似的，dim=1时，diff(A,n,1)也可以简写成diff(A,n)。

注意，diff函数不支持使用'omitnan'参数来忽略向量或者矩阵中的NaN值。

A = [60 65 66 70 68 72 64 70]
A1 = diff(A)        %一阶差分，1可以省略
A2 = diff(A,2)      %二阶差分
A3 = diff(A,3)      %三阶差分
B = randi(9,4,5)
B1 = diff(B)        %计算每列的一阶差分
B2 = diff(b,1,2)    %计算每行的一阶差分

(6)mean:计算平均值（average/mean value）

如果A是一个向量，则mean(A)可以计算向量A的平均值。

如果A是一个矩阵，则mean(A,dim)可以计算A沿维度dim中所有元素的平均值。当dim=1时沿着行方向计算，即得到每列的平均值；当dim=2时沿着列方向计算，即得到每行的平均值。类似的，dim=1时，mean(A,1)也可以简写成mean(A)。

可以在最后加一个输入参数: 'omitnan', 这样计算时会忽略NaN

A = 1:2:9
A1 = mean(A)        %计算向量的平均值
B = randi(9,3,5)
B1 = mean(B)        %计算每列的平均值
B2 = mean(B,2)      %计算每行的平均值

(7)median:计算中位数（median）

中位数又称中值，我们将数据按从小到大的顺序排列，在排列后的数据中居于中间位置的数就是中位数。

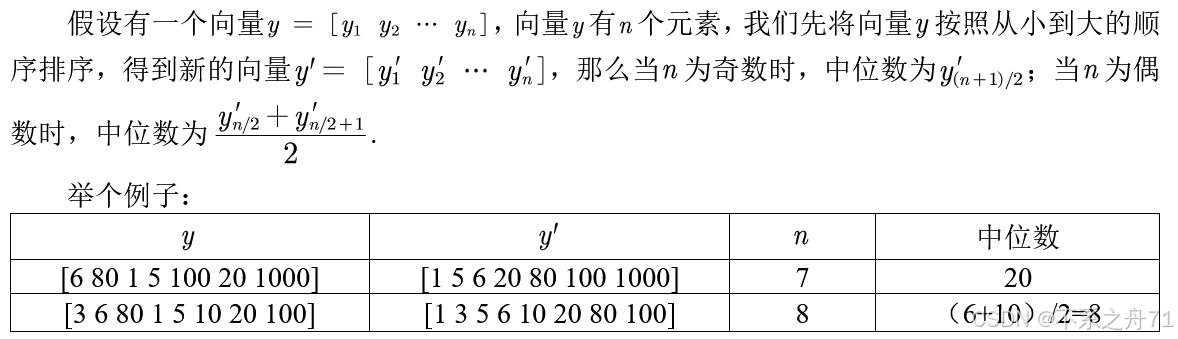
A = [6 80 1 5 100 20 1000]
A1 = median(A)
B = [5 3 -8   4
    1 5 NaN 10; 
    3 6 18  9]
B1 = median(B,1,'omitmissing')      %计算每列的中位数，忽略缺失值，其中1可以省略
B2 = median(B,2,'omitmissing')      %计算每行的中位数，忽略缺失值

(8)mode:计算众数（mode）

众数是指一组数据中出现次数最多的数。一组数据可以有多个众数，例如向量[1 3 -1 2 1 3]中，1和3都出现了两次，它们都是这组数据中的众数。MATLAB中可以使用mode函数计算数据的众数，调用方法也和mean函数类似，但是mode函数可以有多个返回值。以计算向量A的众数为例，直接调用mode(A)会返回A中出现次数最多的值。如果有多个值以相同的次数出现，mode函数将返回其中最小的值。如果A是一个矩阵，则mode(A,1)或者mode(A)可以沿着行方向进行计算，得到每一列的众数；mode(A,2)可以沿着列方向进行计算，得到每一行的众数，这里的1和2表示维度dim。

注意：使用mode函数计算众数时会自动忽略NaN值，我们不能额外添加'omitnan'参数，否则会报错。

用法：

M = mode(A)
M = mode(A,'all')    %M = mode(A,'all') 计算 A 的所有元素的众数。此语法适用于 MATLAB® R2018b 及更高版本。
M = mode(A,dim)      %M = mode(A,dim) 返回维度 dim 上的元素的模式。例如，如果 A 为矩阵，则 mode(A,2) 是包含每一行的出现次数最多值的列向量。
M = mode(A,vecdim)   %M = mode(A,vecdim) 计算向量 vecdim 所指定的维度上的众数。例如，如果 A 是矩阵，则 mode(A,[1 2]) 是 A 中所有元素的众数，因为矩阵的每个元素都包含在由维度 1 和 2 定义的数组切片中。
[M,F] = mode(___)    %[M,F] = mode(___) 支持上述语法中的任何输入参量，且可返回一个频率数组 F。F 与 M 大小相同，而且 F 的每个元素代表 M 中对应元素的出现次数。
[M,F,C] = mode(___)   %[M,F,C] = mode(___) 返回与 M 和 F 同样大小的元胞数组 C。C 中的每个元素都是与 M 中对应元素出现频率相同的所有值的排序向量。

A = [2 3 -1 2 1 3]
A1 = mode(A)
B = randi(9,4,5)
B1 = mode(B,1)      %对每列元素寻找众数
B2 = mode(B,2)      %对每行元素寻找众数
V = [3 3 1 4; 0 0 1 1; 0 1 2 4]
[M,F,C] = mode(V,2)     %C=3×1 cell array
    %{[       3]}
    %{2x1 double}
    %{4x1 double}
m = M   %M = [3;0;0] 每行中的众数
f = F   %F = [2;2;1] 每行众数出现的次数
c_1 = C{1}  %C{1} 为3，因为第一行中值 3 出现的次数为 F(1)            
C_2 = C{2}  %C{2} 为 2×1 向量 [0;1]，因为第二行中值 0 和 1 出现次数为 F(2)。
c_3 = C{3}  %C{3} 为 4×1 向量 [0;1;2;4]，因为第三行中所有值出现次数为 F(3)

(9) var:计算方差(variance)

如果A是一个向量，那么var(A, w)可以计算A的方差，当w=0时，表示计算样本方差，w=1时表示计算总体方差，另外，var(A, 0)也可以直接简写为var(A)。

如果A是一个矩阵，则var(A, w, dim)可以计算矩阵A沿维度dim上的方差。

dim = 1时表示沿着行方向进行计算，即得到每一列的方差；
dim = 2时表示沿着列方向进行计算，即得到每一行的方差。

当dim为1时，var(A, w, 1)可以简写为var(A,w)；若w为0，则可以进一步简写为var(A)，即默认情况下MATLAB会沿行方向计算得到每一列的样本方差。

注意：如果数据中存在NaN值，可以在var函数的最后加上'omitnan'参数来忽略NaN.

V = [6 8 10 12 14];  
V1 = var(V)  % 样本方差，等价于var(v,0)
V2 = var(V,1)  % 总体方差
B = randi(10,4,5)
A1 = var(B)  % 每一列的样本方差,也可以写成var(A,0)或者var(A,0,1) 
A2 = var(B,0,2)  % 每一行的样本方差
B = [9  7    10  10  NaN;
    10  NaN 10  5   10;
    2   3    2   9   8;
    10  6   10    2  10];  
B1 = var(B, 0, 2)  % 计算每一行的样本方差
B2 = var(B, 0, 2, 'omitnan')  % 忽略NaN值计算每一行的样本方差

(10)std:计算标准差（standard deviation）

标准差是方差的算术平方根，它也是用来反应数据离散程度的一个统计量。

既然有了方差为什么还需要标准差呢？这是因为方差和数据原本的量纲（即单位）是不一致的，对方差的计算公式进行量纲分析容易看出，方差的量纲是原始数据量纲的平方，因此对方差开根号，得到的标准差的量纲和原始数据的量纲一致。

在MATLAB中，我们可以使用std函数计算样本标准差和总体标准差，它和var函数的使用方法完全相同。

A = [6 8 10 12 14] 
A1 = std(A)         % 样本标准差，等价于std(v,0)
A2 = std(A,1)       % 总体标准差
C = randi(10,4,5)
B1 = std(C)         % 每一列的样本标准差,也可以写成std(A,0)或者std(A,0,1) 
B2 = std(C,0,2)     % 每一行的样本标准差
C = [9  7    10  10  NaN;
    10  NaN 10  5   10;
    2   3    2   9   8;
    10  6   10    2  10];  

C1 = std(C, 0, 2)  % 计算每一行的样本标准差
C2 = std(C, 0, 2, 'omitmissing') % 忽略NaN值计算每一行的样本标准差

(11)min:求最小值（minimum）

min函数主要有两种用法：

用法一：求两个矩阵对应位置元素的最小值: min(A,B)。矩阵A和矩阵B的大小可以不一样，只要保证矩阵A和矩阵B具有兼容的大小就能够计算

用法二：求向量或者矩阵中的最小值，可以指定沿什么维度计算并返回索引。

1）如果A是向量，则min(A)返回A中的最小值。如果A中有复数，则比较的是复数的模长。

2）如果A是矩阵，则min(A, [ ], 1)沿着A的行方向求每一列的最小值，也可以简写为min(A)；min(A, [ ], 2)沿着A的列方向求每一行的最小值。这里的1和2表示矩阵的维度（dim）。

3）在求向量或矩阵的最小值时，min函数可以有两个返回值：[m, ind] = min(A). 第一个返回值m是我们要求的最小值，ind是最小值在所在维度上的索引。如果最小元素出现多次，则 ind是最小值第一次出现位置的索引。

A = randi(9,3,4)
B = randi(10,3,4)
C = min(A,B)                %取矩阵A、B中的较小的元素形成新矩阵
D = min(A,5)                %取矩阵A与标量5中的较小值
E = min(A,[5,5,5,5])        %取矩阵A与向量[5,5,5,5]中的较小值
F = [5 6 7 3 5 3 10]
f = min(F)                  %向量F中的最小元素
G = [5.5  3+4i  6]          
g = min(G)                  %向量G中存在复数，复数按模长计算
H = randi(9,4,5)
H1 = min(H,[],1)            %矩阵H中每列的最小值
H2 = min(H,[],2)            %矩阵H中每行的最小值
%为什么中间要加一个空向量[ ]? 如果不加的话，就是将A中每个元素和1或者2比较大小，并返回较小值。
I = [5 6 7 3 5 3 10];
[min_I , ind] = min(I)      %求I的最小值并返回索引
J = [ 7  9  2  8
    1  5  1  3
    6  5  8  2];
[min_J , ind] = min(J,[ ],2) %求J每行的最小值并返回索引
j = min(J,[],'all')          %矩阵J的所以元素中最小的，或者min(J(:))
K = [5 6 7 NaN 5 3 10]
[min_K,ind] = min(K)
x = [1  NaN  3   5   2  NaN  1]
y = [2   5   4  NaN  2  NaN  9]
[min_xy,ind] = min(x,y)         %这样会报错：有两个输入数组时，不支持指定两个输出参量。

(12)max:求最大值（maximum）

max函数和min函数的用法相同，它是用来求最大值的函数。

(13)mink

求前k个最小值（这个函数在2017b版本中才推出）

mink是用来求出前k个最小值的函数，它的使用方法类似于我们之前学的一些函数，例如sum和mean函数。

1）如果A是一个向量，则mink(A,k)可以计算向量A的前k个最小值。

2）如果A是一个矩阵，则mink(A,k,dim)可以计算A沿维度dim的前k个最小值。

当dim=1时沿着行方向计算，即得到每列的前k个最小值；

当dim=2时沿着列方向计算，即得到每行的前k个最小值。

类似的，dim=1时，mink(A,k,1)也可以简写成mink(A,k).

A = [1,5,0,4,9,9,3,5,8]
a = mink(A,3)
B = randi(9,5,6)
b1 = mink(B,3,1)        %每列前三个最小的元素
b2 = mink(B,3,2)        %每行前三个最小的元素

(14)maxk

求前k个最大值（这个函数在2017b版本中才推出）

使用方法和mink类似

(15)topkrows

返回矩阵按照排序顺序的前若干行

这个函数的用法和sortrows函数类似，sortrows函数基于某一列对整个矩阵进行排序，而topkrows函数则只返回排序后的前k行（默认是降序排列）。

A = randi(9,3,4)
A1 = topkrows(A,2)        %返回按降序排序的数组A的前2行。
A2 = topkrows(A,1,[3,2],'ascend')

参考：数学建模清风老师《MATLAB教程新手入门篇》https://www.bilibili.com/video/BV1dN4y1Q7Kt/