记录一些基本的公式和概念,不能作为学习概率论的教程。
供个人使用
使用教材:概率论与数理统计教材【西安交通大学出版】
第一章
1.1 随机事件
必然事件( ):在试验中⼀定会发⽣的事件。
不可能事件( ):在试验中不可能发⽣的事件。
概率为0不一定为不可能事件。
事件的运算
- 子事件
- 事件的和、差、积
- 对立事件
- De Morgan対偶法则
1.2 概率
古典概率计算
高中学习的排列组合....
1.3 各种概念&公式
条件概率
全概率
Bayes公式
1.4 事件的独⽴性
第二章
2.1 一维随机变量
离散型
二项分布
泊松分布
二项分布当n足够大的时候,可以近似为泊松分布,
超几何分布
连续型
正态分布
指数分布
指数分布具有无记忆性的特点
均匀分布
2.2 二维随机变量
联合分布律,边缘分布率...
二维正态分布,二维均匀分布
2.3 条件变量
离散型变量
连续型变量
2.4 随机变量的相互独立性
2.5 随机变量函数的概率分布
离散型变量
连续型变量
1个变量的情况:
多个变量的情况:
1.随机变量和的密度函数 Y=X1+X2
2.随机变量商的密度函数 Y=X2/X1
3.max{X1,X2,...} 和 min{X1,X2,X3} 的分布
第四章
4.1 数学期望
离散型数学期望:
连续型数学期望:

数学期望的性质:
1.线性性质(不写了
2.若干个独立随机变量之积的期望等于各变量的期望之积,即
4.2 方差
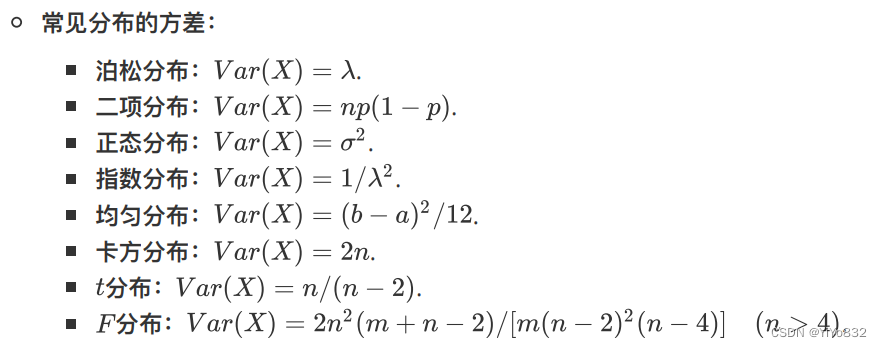
方差的性质:

4.3 协方差,相关系数和矩
协方差

相关系数
相关系数p的定义式为
当p=0时,则称X,Y不相关
矩
原点矩
中心矩
3.4 协方差矩阵
第五章
5.1 大数定理
设是独立同分布的随机变量,记它们的公共均值为a.又设它们的方差存在并记为
.则对任意给定的
>0,有
5.2 中心极限定理
核心公式如下:
第六章
6.1 总体和样本
在一个统计问题里,研究对象的全体叫做总体,构成总体的每个成员称为个体。根据个体的数量指标数量,定义总体的维度,如每个个体只有一个数量指标,总体就是一维的,同理,个体有两个数量指标,总体就是二维的。总体就是一个分布,数量指标就是服从这个分布的随机变量。
假设个变量是相互独立的,则有如下公式:
6.2 常用的统计量
有如下常用统计量:
样本均值
样本方差:
k阶原点矩
k阶中心距
p位数:
次序统计量
-
称为该样本的最小次序统计量;
-
称为该样本的最大次序统计量;
常见性质:
如果总体X的方差和均值均存在,则有如下性质:
6.3 几大分布(重点公式)
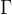 函数
函数
卡方分布
性质(记住)

T分布
性质(记住)
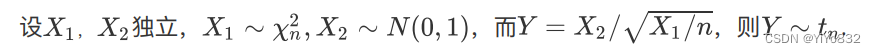
F分布
性质(记住)
设独立,
,而
,则
其他重要性质
1.设独立同分布,有公共的正态分布
.记
.则
2.设的假定同1,则
3.设独立,
各有分布
各有分布
,则
若,则
第七章
7.1 点估计
矩估计
核心思想就是找到各个参数和中心距或者原点矩的关系,用样本矩代替总体矩(可以是原点矩也可以是中心矩);计算出参数。
最大似然估计
核心公式如下:

最大似然估计步骤:
-
写出似然函数;
-
对似然函数取对数,并整理;
-
求参数向量的偏导,令其为0,得到似然方程;
-
求解似然方程,其解为参数值。
7.2 估计量的评选标准
无偏性
还有渐进无偏性
有效性
对于两个估计参数的选取需要基于一个度量无偏估计优劣的准则。有效性作为这样的准则,反映了参数估计值和参数真值的波动,波动大小可用方差来衡量,波动越小表示参数的估计越有效。
可以看到前者方差小,有效性好。
相合性
1.相合估计量或一致估计量
2.均方相合估计量
7.3 区间估计
双侧/单侧区间


常见查表


第八章
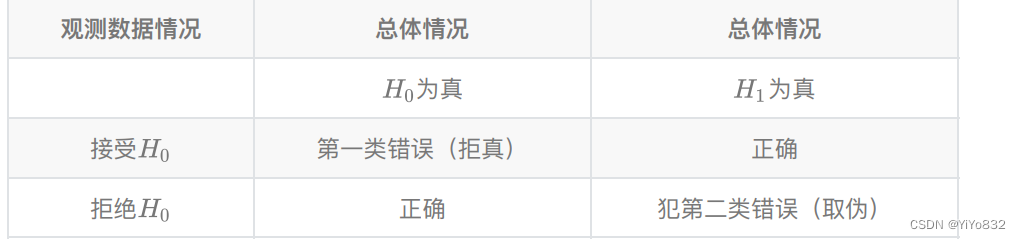
8.1 假设检验的基本概念
在统计上这两个⾮空不相交参数集合称作统计假设,简称假设。通过样本对⼀个假设作 出对与不对的判断,则称为该假设的⼀个检验。若检验结果否定该命题,则称拒绝这个假设,否则 就接受(不拒绝)这个假设。 假设可分为两种:
1. 参数假设检验,即已经知道数据的分布,针对总体的某个参数进⾏假设检验;
2. ⾮参数假设检验,即数据分布未知,针对该分布进⾏假设检验。
建⽴假设—>选择检验统计量,给出拒绝域形式—>选择显著性⽔平—>给出拒绝域—>做出判断
8.2 参数的假设检验
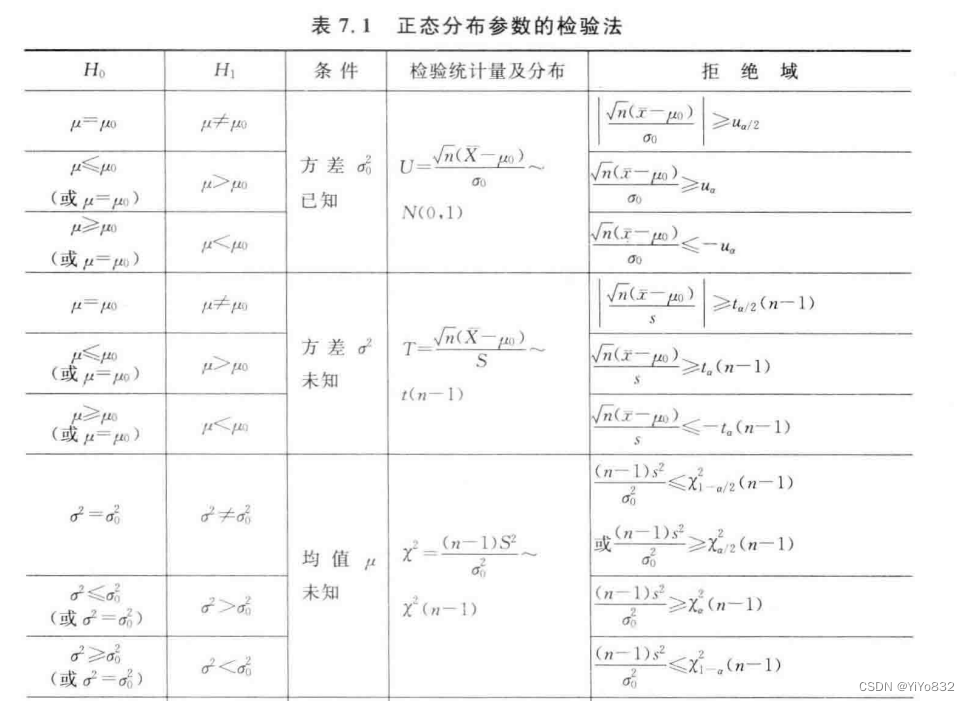
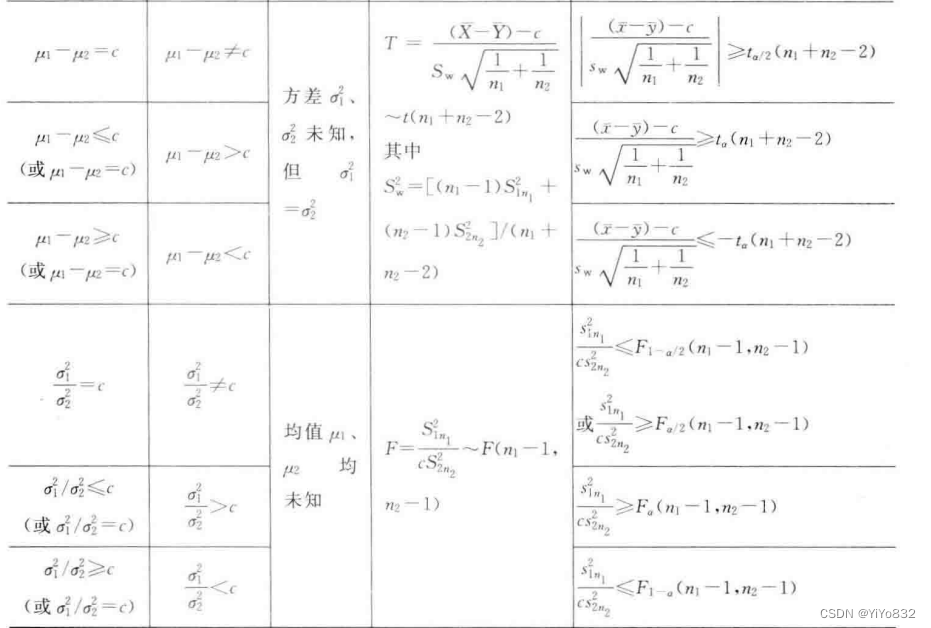
8.3 分布的假设检验

























 162
162

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








