目录
前言:
本篇先进行劝退,需要一些C++语法基础,之后你必须掌握二叉搜索树才能看懂这篇文章。
平衡二叉树非常重要,它是由三个大佬发明的,也称AVL树,它是学习红黑树的基础。本篇主要使用C++的迭代方法实现,当然也会提供递归版本。如果你压根知道什么是平衡二叉树或者只是对它的一些旋转操作有些模糊,请你去B站看看up 蓝不过海呀 的平衡二叉树章节(平衡二叉树(AVL树)_哔哩哔哩_bilibili),看完之后对接下来的学习有帮助。那么接下来,开始学习之旅吧。
一:判断一棵树是否为平衡二叉树
在开始讲解红黑树之前,我们先来做一道题目:力扣-110.平衡二叉树。
这里先说平衡二叉树的定义是什么:左右两棵子树高度差绝对值不超过1。
我们先传入根节点,之后获取左子树高度和右子树高度,并递归判断是否为平衡二叉树,因为本篇重点为如何构建平衡二叉树,所以这里不详细解释只给出代码(伪代码):
int _GetHeight(Node* root)
{
if (root == nullptr)
return 0;
//max (左子树高度, 右子树高度) + 1
int leftH = _GetHeight(root->_left);
int rightH = _GetHeight(root->_right);
return leftH > rightH ? leftH + 1 : rightH + 1;
}
bool _IsBalanceTree(Node* root)
{
if (root == nullptr)
return true;
//看左子树高度和右子树高度差
int leftH = _GetHeight(root->_left);
int rightH = _GetHeight(root->_right);
//获取高度差
int diff = rightH - leftH;
//为了方便调试 我们这里异常就打印出来
if (abs(diff) > 1)
{
return false;
}
return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}二:明确思路
一个好的程序员其实敲代码时间不会很长,最长的的是在敲代码前苦思冥想的时间。
我们这里使用非递归方法,会比递归好想一些,但是鱼与熊掌不可兼得,总要付出一些代价。
1.为什么使用平衡二叉树
我们知道,一般情况下,搜索二叉树的查找时间是O(logN),这个时间复杂度已经很恐怖了。但是存在一种极端情况,就是如果我们插入的都是有序数据时,搜索二叉树就会退化为链表,只有一侧有数据,时间复杂度退化为O(N),这样使用搜索二叉树就没有什么效益了。
为了避免这种极端情况,我们三个大佬就研究出了一种平衡树,也就是之前说的左右子树高度差绝对值不超过1。
2.旋转
此时有{ 1, 2, 3 }这3个数据插入树(以下我们说的树都是平衡二叉搜索树)中,你会发现他们都在一边。

此时该怎么办?对没错,就是旋转。
2.1 左旋
上述情况,我们可以将根节点向左旋转,将 “2” 作为新的根节点:

2.2 右旋
如果我们插入的是 { 3, 2, 1 } 呢?聪明的你肯定想到了就右旋这棵树:

那么好,恭喜你已经掌握了两个最基本的武器,我们就是利用这两个武器来完成平衡树的!
3.冲突节点
你肯定还有疑问?就这?没有其他情况了?有。我们先不考虑树很高的情况,这里先把冲突节点的问题解决。当我们左旋时,根节点的右孩子的左节点(有些拗口,不过大家可以看图)可能会存在节点,这是根节点向左旋就会产生冲突,所以这里有一个口诀:冲突的左孩变右孩。
也就是说,当左旋时有冲突节点,该节点变成根节点的右孩子(别急看图,原谅作者不会搞动画,必须抽空学习一下了!)。

(以上图中,subR表示parent右孩子,subRL表示subR的左孩子,下面例子中,我们都这样举例)
当然,右旋的话就是冲突的右孩变左孩:

4.平衡因子
既然我们已经知道了如何旋转,旋转的时候如何解决冲突。但是我们怎么知道什么时候进行旋转呢?这时候我们就需要用到平衡因子了。也就是说,每个节点中都有一个成员变量,就是平衡因子,它是判断我们是否需要旋转树的关键。
我们想:是不是当前树的左子树高度和右子树高度差绝对值大于2时,就应该旋转了?对,没错。但是我们要计算出平衡因子的具体值,这样才能知道该如何旋转它。
本篇使用的 平衡因子_bf = 右子树高度 - 左子树高度。
所以,是不是当_bf(平衡因子)为2时,我们至少知道此时应该左旋这个节点;反之_bf为-2时,该右旋这个节点(当然有其他情况,不过我们后面补充)。
5.双旋
我们之前已经说明了两种情况:左旋 和 右旋。
它们是最基本的单旋,我们将所有节点标注上_bf再次观察:
(当没有冲突节点时左旋)

(当有冲突节点时左旋)

(当有没冲突节点时右旋)

(当有冲突节点时右旋)

但是难道只有这两种情况吗?当然还有其他情况,比如我们一开始就是这样插入的:
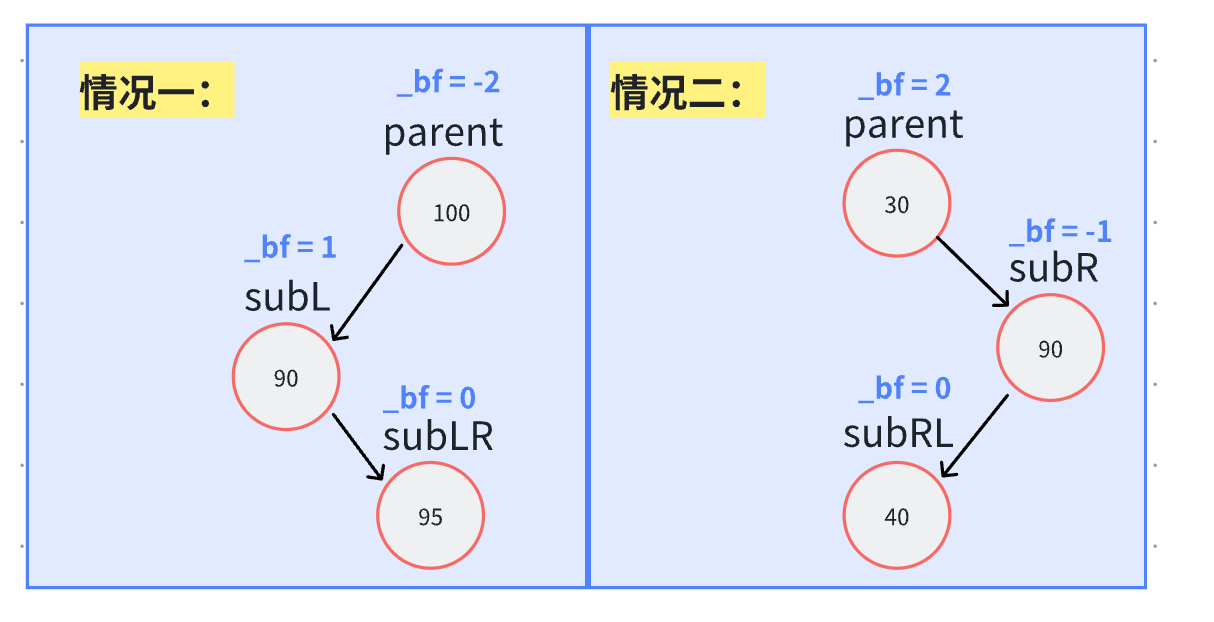
你可能会想,对情况一右旋,情况二左旋会不会解决问题?

你会发现无论如何使用左旋和右旋都解决不了,所以以上方法不行,但是怎么办呢?
此时我们需要对其旋转两次,就情况一而言,首先是对subL左旋,之后对parent右旋。
5.1 左右双旋(LR)
对情况一而言,我们需要对subL先左旋,之后右旋:

通过上图我们发现,最终还是会转换为单旋。
5.2 右左双旋(RL)

通过上图我们可以发现(parent的孩子通通以cur统称) ,当cur和parent的平衡因子异号时,需要双旋,同号时,只需要单旋。
所以其实一共有以下四种情况:

而且我们可以发现,LL型进行右单旋;RR型进行左单旋;LR型先左旋后右旋;RL型先右旋后左旋。
6.平衡因子的更新
本篇主要讲解迭代法,那么_bf该如何更新呢?
我们可以发现,根据本篇的规则,当向右边插入,该节点_bf应当自增1,当向左边插入应当自减1。因为树要保持平衡,所以我们插入节点时,当当前节点不是非常平衡时(也就是1或者-1时)应当继续向上调整,比如:

或者另一种情况:

但是如果 _bf == 0 时,则说明不用继续向上更新,因为此时两边平衡,没有必要更新。
7.冲突节点问题补充
大家看到这里可以想一下,这里我们会循环调整,所以我们最开始说的单旋那种有冲突节点的情况会存在吗?对,根本不存在!因为有冲突节点的之前树就已经被调整到平衡状态了,那么是否说明我们可以不考虑冲突节点了呢?并不是,比如以下这棵树:
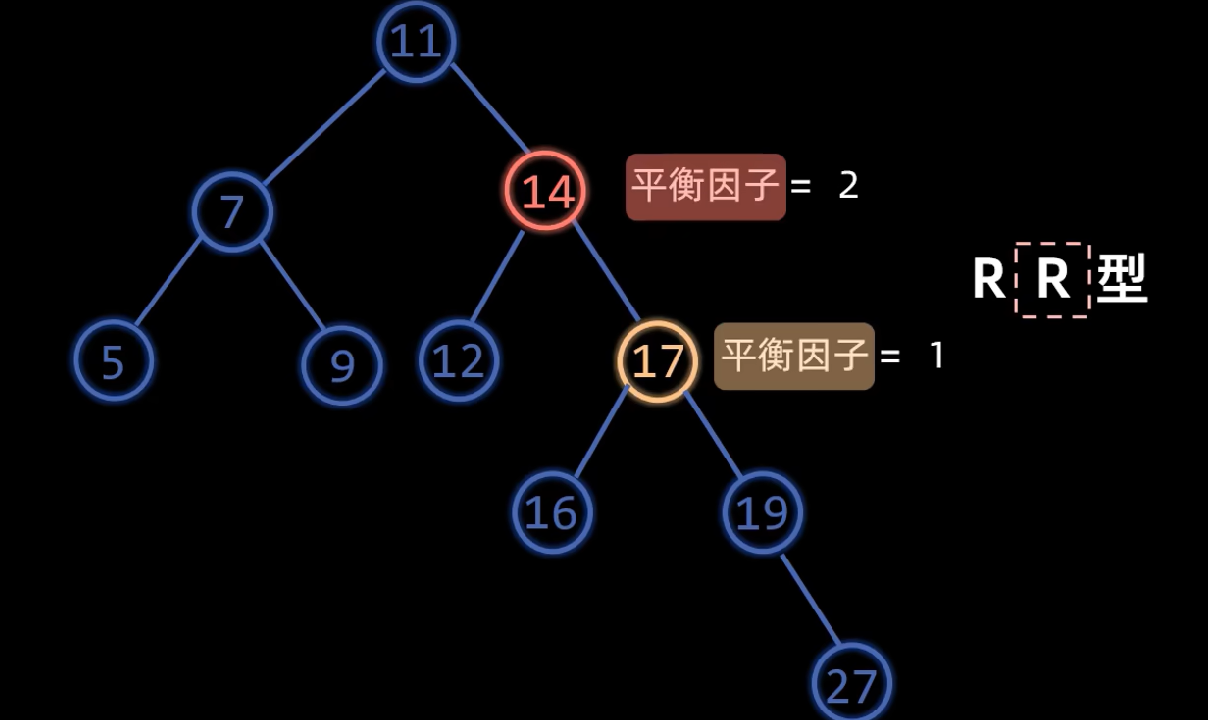
此时有冲突节点,我们左旋:

其实这里有一个结论:只要旋转,就不用继续往上调整了!
也就意味着我们只要进行了旋转操作,树就平衡了。
三:创建平衡二叉树
1.定义树节点
我们要明确思路,因为是迭代法,我们要去找父节点,所以这里我们定义树要有三个指针,左孩子,右孩子和父母,因为要调整树的平衡,所以要有平衡因子来作为判断旋转的依据,所以我们这样定义树节点(这里使用pair作为对象,是为了能够存储键值对,所以提供两个模板参数)。
成员变量名称前加上 "_" 方便和后面作区分。
template<class K, class V>
struct AVLTreeNode
{
pair<K, V> _kv;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
int _bf; // balance factor
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
{}
};这样树节点就定义好了。
2.定义树
因为树节点名称太长,所以这里现对其重命名。树中成员有一个根节点即可。使用编译器提供的默认构造方法。
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
AVLTree() = default;
private:
Node* _root = nullptr;
};3.插入节点
插入节点非常复杂,因为我们会去调整树,对其旋转,所以这里先按照二叉搜索树的逻辑写一个插入方法:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent; //记得更新其父节点
return true;
}这里就是二叉搜索的逻辑,只不过是加上了_parent的修改,这里不在赘述。
3.1 平衡因子的迭代调整
当我们插入节点时,上面讲到,如果平衡因子为-1或者1时,要迭代向上调整;为0时无需调整;为-2或2时旋转树且只旋转一次,所以我们先把大逻辑写好:
//因为可能更新到根
// 更新平衡因子
while (parent)
{
if (cur == parent->_left)
parent->_bf--;
else
parent->_bf++;
if (parent->_bf == 0)
{
break; //已经平衡 无需处理
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
// 继续往上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 不平衡了,旋转处理
//...
//旋转完以后就不用处理了
break;
}
else
{
//此时旋转也解决不了问题 直接报错
assert(false);
}
}3.2 左单旋方法(RR类型)
当 parent->_bf == 2 && cur->_bf == 1 此时是RR类型,我们要进行左旋操作。
这里我们完善左旋函数(因为左旋使用者不会调用也不能调用,所以写成私有函数):
//这里我们使用的非递归 所以一种4种情况 我们每个都单独写一遍
//先写LL 左单旋
void RotateL(Node* parent)
{
//这里需要记录传入节点的父节点
Node* parentP = parent->_parent;
//先把大逻辑写好 这里和递归的左旋逻辑一样 但是需要考虑的情况很多
//比如 _bf平衡因子 _parent 等
Node* subR = parent->_right; //还是一样 先记录要作为根节点的值
Node* subRL = subR->_left; //之后记录冲突节点
parent->_right = subRL; //冲突的左孩变右孩
subR->_left = parent; //新根左孩是旧根
//先考虑所有节点的 父节点 最先考虑subR, subRL
//因为subRL可能为空 所以判断一下
if (subRL)
{
subRL->_parent = parent;
}
parent->_parent = subR; //这一步不需要判断 当不平衡时旋转 parent绝不为空
//此时需要判断parentP是否为空
if (parentP)
{
//不为空时 subR作为新的根节点 一定要改变其parent
subR->_parent = parentP;
//此时不为空 需要判断 parent 在 parentP 的哪一边
if (parent == parentP->_left)
{
//在左边
parentP->_left = subR;
}
else
{
//在右边
parentP->_right = subR;
}
}
else
{
//此时parentP为空 旋转好的节点作为根节点
_root = subR;
//还需要更新subR->_parent
subR->_parent = nullptr;
}
//之后就是_bf的更新了
//parent的高度降低了 这里是直接降低了2层 因为我们是 == 2/-2 所以直接置0
parent->_bf = 0;
//新的根节点变平衡了 所以也置零
subR->_bf = 0; //之后后面会向上更新
}因为冲突节点可能为空,所以我们要单独判断。而且我们发现,单旋只有两个节点高度改变,且调整完之后高度平衡,所以更新两个高度改变节点的_bf,都是0。
还要记得更新_parent节点。且可能要改变根节点(大家可以看一下注释,很清楚)。
3.3 右单旋方法(LL类型)
当 parent->_bf == -2 && cur->_bf == -1 此时是LL类型,我们要进行右旋操作。这里我们完善右旋函数:
//RR 右单旋
void RotateR(Node* parent)
{
//还是要记录传入节点的父节点
Node* parentP = parent->_parent;
//还是先把大逻辑写好
//这里是冲突的右孩变左孩
Node* subL = parent->_left;
Node* subLR = subL->_right;
//之后开始旋转
subL->_right = parent;
parent->_left = subLR;
//之后还是一样 先考虑他们_parent
parent->_parent = subL;
//先考虑 subLR 是否为空
if (subLR)
{
subLR->_parent = parent;
}
//考虑传入节点是否为根节点
if (parent == _root)
{
subL->_parent = nullptr;
_root = subL;
}
else
{
//判断在传入节点的哪一侧
if (parent == parentP->_left)
{
parentP->_left = subL;
}
else
{
parentP->_right = subL;
}
subL->_parent = parentP; //记得更新新根节点的_parent
}
//之后就是 _bf 平衡因子 只有两个改变了 都变为了0
parent->_bf = 0;
subL->_bf = 0;
}这里和左旋就是镜像了。
为了方便各位理解,这里使用抽象图来说明插入的一些情况。
3.4 RL双旋抽象图

①当 h = 0 时:


也就意味着a,b,c,d没有节点,60就是当前插入的节点。此时RL双旋后,该树平衡。
所以我们如果写RL函数,里面可以复用左单旋和右单旋,但是我们要更新_parent和_bf,但是我们之前写的单旋函数里面都会改变调整节点的_bf, 所以我们要在旋转前记录_bf。至于记录哪个,其实就是插入节点(cur)的_bf。
//RL 右左双旋 void RotateRL(Node* parent) { //记住 在外满足条件 parent->_bf == 2 && cur->_bf == -1 才会使用这个双旋 //此时我们要判断cur->_left的平衡因子来更新新的平衡因子 //这里我们还需要改变平衡因子 必须在旋转之前拿到平衡因子 Node* subR = parent->_right; Node* subRL = subR->_left; int bf = subRL->_bf; //关键就看要插入节点的parent的平衡因子 //我们直接复用代码即可 RotateR(subR); //先将右节点右旋 RotateL(parent); //再将传入节点左旋 //... }
②当 h = 1 时:
⑴此时插入的位置在右边:
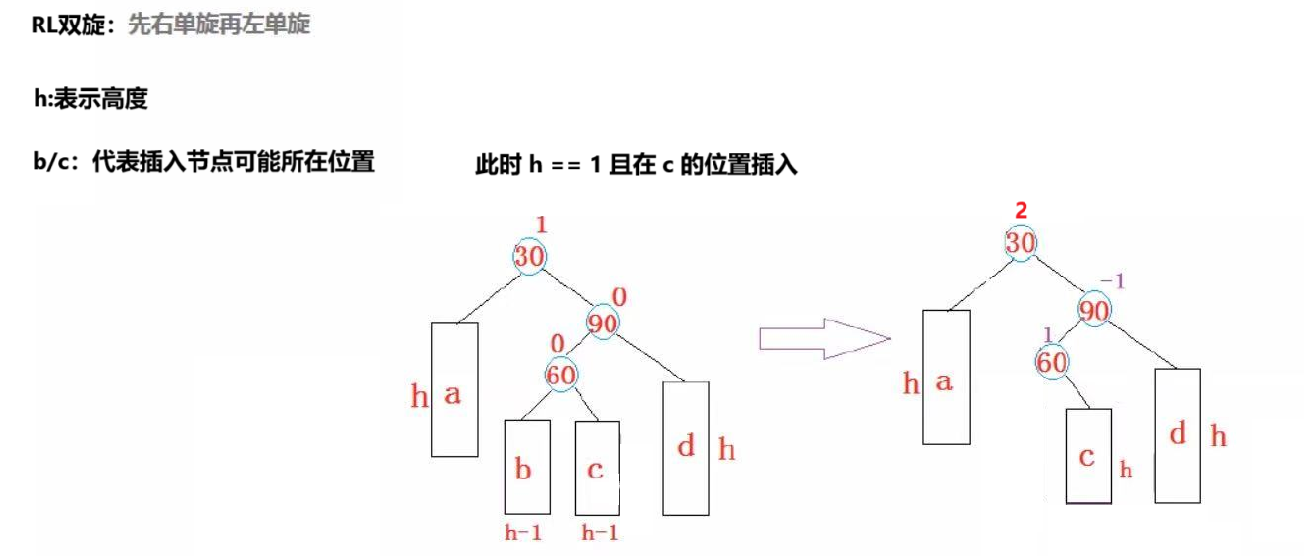

⑵此时插入的位置在左边:


所以此时我们就可以给出RL方法了:
//RL 右左双旋
void RotateRL(Node* parent)
{
//记住 在外满足条件 parent->_bf == 2 && cur->_bf == -1 才会使用这个双旋
//此时我们要判断cur->_left的平衡因子来更新新的平衡因子
//这里我们还需要改变平衡因子 必须在旋转之前拿到平衡因子
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf; //关键就看要插入节点的parent的平衡因子
//我们直接复用代码即可
RotateR(subR); //先将右节点右旋
RotateL(parent); //再将传入节点左旋
if (bf == 0)
{//这时的情况就是
// a ----> parent
// \
// b ----> subR
// /
// c ----> subRL c就是新插入的节点 最后一定平衡
subR->_bf = 0;
subRL->_bf = 0;
parent->_bf = 0;
//之后就是其他的插入情况 就是可能会插入 c 的左边或者右边
//所以我们就要通过subRL(c)的平衡因子来判断情况
}
else if (bf == 1)
{
//这里是插入 c 的右边
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
//这里是插入 c 的左边
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else
{
assert(false);
}
}③当 h = 2 时:
我们先来观察抽象图,当 h = 2 时:

RL双旋总结:
其实最终就像我们之前 h = 1 一样,最终subRL都会变为新的根节点,所以调整后一定两边平衡,也就是说 subRL->_bf = 0 。
而subR->_bf 和 parent->_bf 是根据插入节点在 subRL 左边还是右边决定的(以 h = 1 为例)。
- 当插入 subRL 的右边时(subRL->_bf = 1),最终会使插入节点在 subR 的左边,从而 subR->_bf = 0 。而 parent->_bf = -1 。
- 当插入 subRL 的左边时(subRL->_bf = -1),最终会使插入节点在 parent 的右边,从而 parent->_bf = 0 。而 subR->_bf = 1 。
- 最终 subRL 都会变为新的根节点,左右两边平衡,所以 subRL->_bf = 0 。
3.5 LR双旋抽象图

①当 h = 0 时:


②当 h = 1 时:
⑴此时插入的位置在右边:


⑵此时插入的位置在左边:


这里就不介绍 h = 2 了,因为和RL是一样的。
所以我们给出LR方法:
//LR 左右双旋
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
//旋转之前需要记录 subLR 的平衡因子
int bf = subLR->_bf;
//先对parent的左边节点左旋
RotateL(subL);
RotateR(parent); //再对parent右旋
//当原来只有三个节点时 最后每个平衡因子都是0
if (bf == 0)
{
// a
// /
// b
// \
// c
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
//此时插入节点在 c 的右边
subL->_bf = -1;
subLR->_bf = 0;
parent->_bf = 0;
}
else if (bf == -1)
{
//此时插入节点在 c 的左边
subL->_bf = 0;
subLR->_bf = 0;
parent->_bf = 1;
}
else
{
assert(false);
}
}LR双旋总结:
但是我们最终都可以得出和RL类似的结果:
最终subLR都会变为新的根节点,所以调整后一定两边平衡,也就是说 subLR->_bf = 0 。
而subL->_bf 和 parent->_bf 是根据插入节点在 subLR 左边还是右边决定的(以 h = 1 为例)。
- 当插入 subLR 的右边时(subLR->_bf = 1),最终会使插入节点在 parent 的左边,从而 parent->_bf = 0 。而 subL->_bf = -1 。
- 当插入 subLR 的左边时(subLR->_bf = -1),最终会使插入节点在 subL 的右边,从而 subL->_bf = 0 。而 parent->_bf = 1 。
- 最终 subLR 都会变为新的根节点,左右两边平衡,所以 subLR->_bf = 0 。
4.其他方法(拷贝构造)
之后就是其他方法了,比如拷贝构造了,Find查找函数了,等等。你可能会问,删除呢?哈哈,这个小编精力有限,等有空了再搞定。这里其他方法对各位而言应该轻而易举,这里就不在一一赘述。
这里还是要强调和其他树的拷贝构造不同的是,我们要考虑其 _bf 和 _parent ,这里我们需要多添加几条语句:
四:AVL树迭代方法全部代码
这里先给出头文件(AVLTree.h)代码:
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
template<class K, class V>
struct AVLTreeNode
{
pair<K, V> _kv;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
int _bf; // balance factor
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
{}
};
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
AVLTree() = default;
AVLTree(const AVLTree<K, V>& t)
{
_root = Copy(t._root);
}
AVLTree<K, V>& operator=(AVLTree<K, V> t)
{
swap(_root, t._root);
return *this;
}
~AVLTree()
{
Destroy(_root);
_root = nullptr;
}
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//因为可能更新到根
// 更新平衡因子
while (parent)
{
if (cur == parent->_left)
parent->_bf--;
else
parent->_bf++;
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
// 继续往上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 不平衡了,旋转处理
if (parent->_bf == 2 && cur->_bf == 1)
{
//左旋
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
//右旋
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
//可以发现规律 同号单旋 异号双旋
//这里我们先把步骤写全 RL 右左双旋
RotateRL(parent);
}
else
{
//左右双旋
RotateLR(parent);
}
//旋转完以后就不用处理了
break;
}
else
{
//此时旋转也解决不了问题 直接报错
assert(false);
}
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
//写一个中序遍历
void Inorder()
{
//写一个子函数
_Inorder(_root);
cout << endl;
}
void Preorder()
{
_Preorder(_root);
cout << endl;
}
//写一函数 检查自己是否是平衡树
bool IsBalanceTree()
{
return _IsBalanceTree(_root);
}
//获取树高
int GetHeight()
{
return _GetHeight(_root);
}
private:
//因为没有必要给用户提供旋转、销毁等函数 所以写成私有的
int _GetHeight(Node* root)
{
if (root == nullptr)
return 0;
//max (左子树高度, 右子树高度) + 1
int leftH = _GetHeight(root->_left);
int rightH = _GetHeight(root->_right);
return leftH > rightH ? leftH + 1 : rightH + 1;
}
bool _IsBalanceTree(Node* root)
{
if (root == nullptr)
return true;
//看左子树高度和右子树高度差
int leftH = _GetHeight(root->_left);
int rightH = _GetHeight(root->_right);
//获取高度差
int diff = rightH - leftH;
//if (abs(diff) > 1 || root->_bf != diff)
// return false; //这里顺便把平衡因子检查了
//为了方便调试 我们这里异常就打印出来
if (abs(diff) > 1)
{
cout << root->_kv.first << "高度差异常" << endl;
return false;
}
if (root->_bf != diff)
{
cout << root->_kv.first << "平衡因子异常" << endl;
return false;
}
return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << " ";
_Inorder(root->_right);
}
void _Preorder(Node* root)
{
if (root == nullptr)
return;
cout << root->_kv.first << ":" << root->_kv.second << " ";
_Preorder(root->_left);
_Preorder(root->_right);
}
//这里我们使用的非递归 所以一种4种情况 我们每个都单独写一遍
//先写LL 左单旋
void RotateL(Node* parent)
{
//这里需要记录传入节点的父节点
Node* parentP = parent->_parent;
//先把大逻辑写好 这里和递归的左旋逻辑一样 但是需要考虑的情况很多
//比如 _bf平衡因子 _parent 等
Node* subR = parent->_right; //还是一样 先记录要作为根节点的值
Node* subRL = subR->_left; //之后记录冲突节点
parent->_right = subRL; //冲突的左孩变右孩
subR->_left = parent; //新根左孩是旧根
//先考虑所有节点的 父节点 最先考虑subR, subRL
//因为subRL可能为空 所以判断一下
if (subRL)
{
subRL->_parent = parent;
}
parent->_parent = subR; //这一步不需要判断 当不平衡时旋转 parent绝不为空
//此时需要判断parentP是否为空
if (parentP)
{
//不为空时 subR作为新的根节点 一定要改变其parent
subR->_parent = parentP;
//此时不为空 需要判断 parent 在 parentP 的哪一边
if (parent == parentP->_left)
{
//在左边
parentP->_left = subR;
}
else
{
//在右边
parentP->_right = subR;
}
}
else
{
//此时parentP为空 旋转好的节点作为根节点
_root = subR;
//还需要更新subR->_parent
subR->_parent = nullptr;
}
//之后就是_bf的更新了
//parent的高度降低了 这里是直接降低了2层 因为我们是 == 2/-2 所以直接置0
parent->_bf = 0;
//新的根节点变平衡了 所以也置零
subR->_bf = 0; //之后后面会向上更新
}
//因为要把所有的旋转情况都写一遍 所以这里写右单旋 RR
//RR 右单旋
void RotateR(Node* parent)
{
//还是要记录传入节点的父节点
Node* parentP = parent->_parent;
//还是先把大逻辑写好
//这里是冲突的右孩变左孩
Node* subL = parent->_left;
Node* subLR = subL->_right;
//之后开始旋转
subL->_right = parent;
parent->_left = subLR;
//之后还是一样 先考虑他们_parent
parent->_parent = subL;
//先考虑 subLR 是否为空
if (subLR)
{
subLR->_parent = parent;
}
//考虑传入节点是否为根节点
if (parent == _root)
{
subL->_parent = nullptr;
_root = subL;
}
else
{
//判断在传入节点的哪一侧
if (parent == parentP->_left)
{
parentP->_left = subL;
}
else
{
parentP->_right = subL;
}
subL->_parent = parentP; //记得更新新根节点的_parent
}
//之后就是 _bf 平衡因子 只有两个改变了 都变为了0
parent->_bf = 0;
subL->_bf = 0;
}
//RL 右左双旋
void RotateRL(Node* parent)
{
//记住 在外满足条件 parent->_bf == 2 && cur->_bf == -1 才会使用这个双旋
//此时我们要判断cur->_left的平衡因子来更新新的平衡因子
//这里我们还需要改变平衡因子 必须在旋转之前拿到平衡因子
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf; //关键就看要插入节点的parent的平衡因子
//我们直接复用代码即可
RotateR(subR); //先将右节点右旋
RotateL(parent); //再将传入节点左旋
if (bf == 0)
{//这时的情况就是
// a ----> parent
// \
// b ----> subR
// /
// c ----> subRL c就是新插入的节点 最后一定平衡
subR->_bf = 0;
subRL->_bf = 0;
parent->_bf = 0;
//之后就是其他的插入情况 就是可能会插入 c 的左边或者右边
//所以我们就要通过subRL(c)的平衡因子来判断情况
}
else if (bf == 1)
{
//这里是插入 c 的右边
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
//这里是插入 c 的左边
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
//LR 左右双旋
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
//旋转之前需要记录 subLR 的平衡因子
int bf = subLR->_bf;
//先对parent的左边节点左旋
RotateL(subL);
RotateR(parent); //再对parent右旋
//当原来只有三个节点时 最后每个平衡因子都是0
if (bf == 0)
{
// a
// /
// b
// \
// c
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
//此时插入节点在 c 的右边
subL->_bf = -1;
subLR->_bf = 0;
parent->_bf = 0;
}
else if (bf == -1)
{
//此时插入节点在 c 的左边
subL->_bf = 0;
subLR->_bf = 0;
parent->_bf = 1;
}
else
{
assert(false);
}
}
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newNode = new Node(root->_kv);
newNode->_left = Copy(root->_left);
newNode->_right = Copy(root->_right);
//记得赋值平衡因子
newNode->_bf = root->_bf;
//更新_parent
if (newNode->_left)
newNode->_left->_parent = newNode;
if (newNode->_right)
newNode->_right->_parent = newNode;
return newNode;
}
private:
Node* _root = nullptr;
};之后是测试文件:
#include"AVLTree.h"
void testAVL()
{
AVLTree<int, int> t;
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 14, 9, 5, 17, 11, 12, 7, 19, 16, 27 };
for (auto e : a)
{
t.Insert({ e, e });
//cout << e << t.IsBalanceTree() << endl; //方便调试报错
}
cout << "中序遍历为:";
t.Inorder();
cout << "前序遍历为:";
t.Preorder();
if (t.IsBalanceTree())
{
cout << "t是平衡树" << endl;
}
else
{
cout << "t不是平衡树" << endl;
}
if (t.Find(2)) //只是测试Find代码
{
cout << "2是树中节点" << endl;
}
else
{
cout << "2不是树中节点" << endl;
}
cout << "测试拷贝构造" << endl;
AVLTree<int, int> t1(t);
if (t1.IsBalanceTree())
{
cout << "t1是平衡树" << endl;
}
else
{
cout << "t1不是平衡树" << endl;
}
}
int main()
{
testAVL();
return 0;
}以上数组构建的AVL树为:

其运行结果为:

总结:
本来小编想把使用C语言递归方式创建AVL树写出来,但是代码粘贴上去之后发现太多了,有机会在写一篇相关文章吧。
如果你能看到这,恭喜你,你几乎可以独立写出AVL树了,非递归方法很复杂,但是我们理解的就会很好,之后,我们就可以进阶到红黑树了,这是你成为数据结构大佬的重要一环,大家敬请期待!
麻烦您动动小手点个赞吧,写了快2天,真的不容易,谢谢老铁焖支持!
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








