力扣热题100之盛最多水的容器

题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

代码

方法一

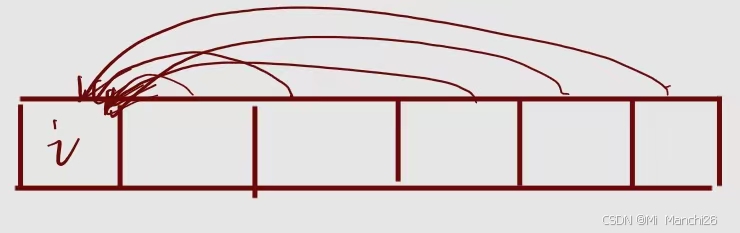
依次遍历到倒数第二个数，这种方法的时间复杂度较大，差不多是O(n的平方)

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_area=0
        for i in range(len(height)-1):
            for j in range(len(height)-1, i, -1):
                cur_area=(j-i)*min(height[i],height[j])
                if max_area<cur_area:
                    max_area=cur_area
        return max_area          

方法二

思想和方法一一致都是双指针左右两边往中间走，但是可以根据木桶效应将上面的两个for循环简化：
重点就是如何移动指针：每次比较左右指针的高度，移动较矮的一侧的指针。

因为容器的面积受限于较矮的一侧。如果保持较矮的一侧不动，移动高的一侧，容器的面积只会因为宽度减小而更小（因为这时高度没变，或者时因为移动高的一侧高度变得更小）。只有移动较矮的一侧，才有可能在后续找到更高的垂线，从而抵消宽度减小的影响，甚至获得更大的面积。

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_area=0
        left,right=0,len(height)-1
        while left<right:
            cur_area=(right-left)*min(height[right],height[left])
            if height[right]<height[left]:
                right-=1
            else:
                left=+1
            max_area=max(cur_area,max_area)
        return max_area