R语言单位根检验详细版

5%的玄学

于 2023-12-07 22:21:18 发布

阅读量4.7k

点赞数 54

文章标签： java 前端 javascript r语言

本文链接：https://blog.csdn.net/weixin_64832161/article/details/134825177

版权

一、数据

1978-2002年中国农村居民家庭人均纯收入对数序列{}和生活消费支出对数序列{}的相对变化关系如下表所示。

year	x	y	lnx	lny
1978	133.6	116.1	4.89485	4.754452
1979	160.7	134.5	5.079539	4.901564
1980	191.3	162.2	5.253843	5.08883
1981	223.4	190.8	5.408964	5.251226
1982	270.1	220.2	5.598792	5.394536
1983	309.8	248.3	5.735927	5.514638
1984	355.3	273.8	5.872963	5.612398
1985	397.6	317.4	5.985446	5.760163
1986	423.8	357	6.049262	5.877736
1987	462.6	398.3	6.136863	5.987205
1988	544.9	476.7	6.300602	6.166887
1989	601.5	535.4	6.399427	6.283014
1990	686.3	584.6	6.531315	6.370928
1991	708.6	619.8	6.563291	6.429397
1992	784	659.8	6.664409	6.491937
1993	921.6	769.7	6.826111	6.646001
1994	1221	1016.8	7.107425	6.924416
1995	1577.7	1310.4	7.363723	7.178088
1996	1926.1	1572.1	7.563253	7.360168
1997	2090.1	1617.2	7.644967	7.388452
1998	2162	1590.3	7.678789	7.371678
1999	2210.3	1577.4	7.700884	7.363533
2000	2253.4	1670.1	7.720195	7.420639
2001	2366.4	1741	7.769125	7.462215
2002	2476	1834	7.8144	7.514255

二、画时序图

```{r}
library(readxl)
b<-read_excel("C:/Users/Lenovo/Desktop/A1_27.xlsx")
x<-ts(b$lnx,start = 1978)   #人均纯收入对数序列
y<-ts(b$lny,start = 1978)   #消费支出对数序列
c1<-min(x,y)
c2<-max(x,y)
plot(x,ylim=c(c1,c2),col=1,ylab="x,y")
lines(y,lty=2,col=2)
legend("topleft",legend=c("居民家庭人均纯收入对数序列","居民生活消费支出对数序列"),col=c(1,2),lty=c(1,2),bty="n");
```

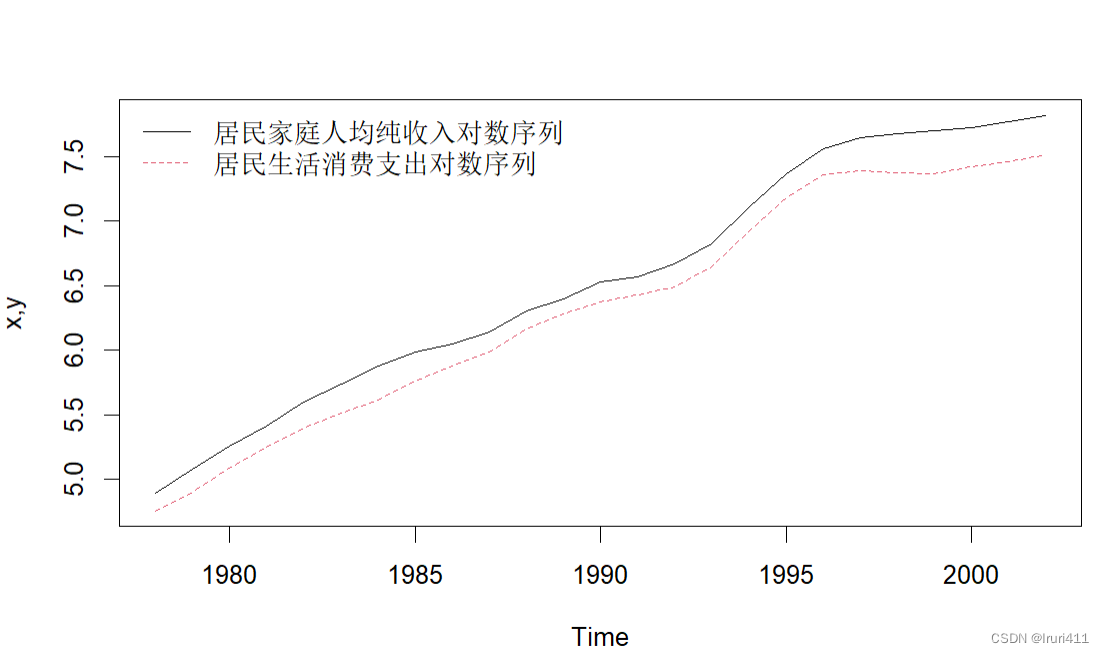
三、检验是否平稳

对序列的平稳性检验主要分为两种检验方法:一种根据时序图和自相关图的特征做出判断的图检验方法；另一种是构造检验统计量进行假设检验的方法。本文主要以第二种检验方式为主进行介绍，第一种方法较简单且具有主观性。

单位根检验

常用的单位根检验包括DF检验、ADF检验、PP检验、KPSS检验

1.DF检验

ADF检验原假设和备择假设
情形	原假设	备择假设
I	含单位根的非平稳时间序列	零均值平稳时间序列
II	含单位根的非平稳时间序列	非零均值平稳时间序列
III	含单位根的非平稳时间序列	趋势平稳序列

(1)当序列基本走势呈现无规则上升或下降并反复时，将其归于为无漂移项自回归模型

(2)当序列基本走势呈现明显的随时间递增或递减且趋势不太陡峭时，将其归为带漂移项自回归模型

(3)当序列基本走势随时间快速递增时，则将其归为带趋势项回归过程

```{r}
library(fBasics)
library(fUnitRoots)
adfTest(x,lag=1,type="nc")  #无漂移项
adfTest(x,lag=1,type="c")   #带漂移项
adfTest(x,lag=1,type="ct")  #带漂移项和趋势项
```

p值> $\alpha$ ，接受原假设，该序列不平稳。

2.ADF检验

在R语言中，fUnitRoots程序包中的函数adfTest( )、urca程序包中的函数ur.df( )、aTSA程序包中的函数adf.test( )以及tseries程序包中的函数adf.test( )均可进行ADF检验。具体函数命令格式可以在rstudio中通过(?程序命令)进行查找与学习。由于ADF检验有一个基本假定Var( $\varepsilon _t$ )= $\sigma ^2$ ，这导致ADF检验主要适用于方差齐性，对异方差序列的平稳性检验效果不佳。

ADF检验原假设和备择假设
情形	原假设	备择假设
I	含单位根的非平稳时间序列	零均值平稳时间序列
II	含单位根的非平稳时间序列	非零均值平稳时间序列
III	含单位根的非平稳时间序列	趋势平稳序列

p值< $\alpha$ ，拒绝原假设，p值> $\alpha$ ,接受原假设， $\alpha$ 一般取0.05

```{r}
library(aTSA)
adf.test(x)  #x表示居民人均收入对数序列
```

上述Type1,Type2,Type3对应上述三种情形，由上述结果可以看出所有p值都> $\alpha$ ,所以不平稳。

如果p值均小于 $\alpha$ ，则选取p值最小的那种类型，p值越小越有把握拒绝原假设

```{r}
library(fBasics)
library(fUnitRoots)
adfTest(x,lag=1,type="nc")   #nc表示无漂移项(没有常数项)第一种类型
adfTest(x,lag=1,type="c")    #c表示有漂移项(常数项)第二种类型
adfTest(x,lag=1,type="ct")   #ct表示带趋势项第三种类型
```

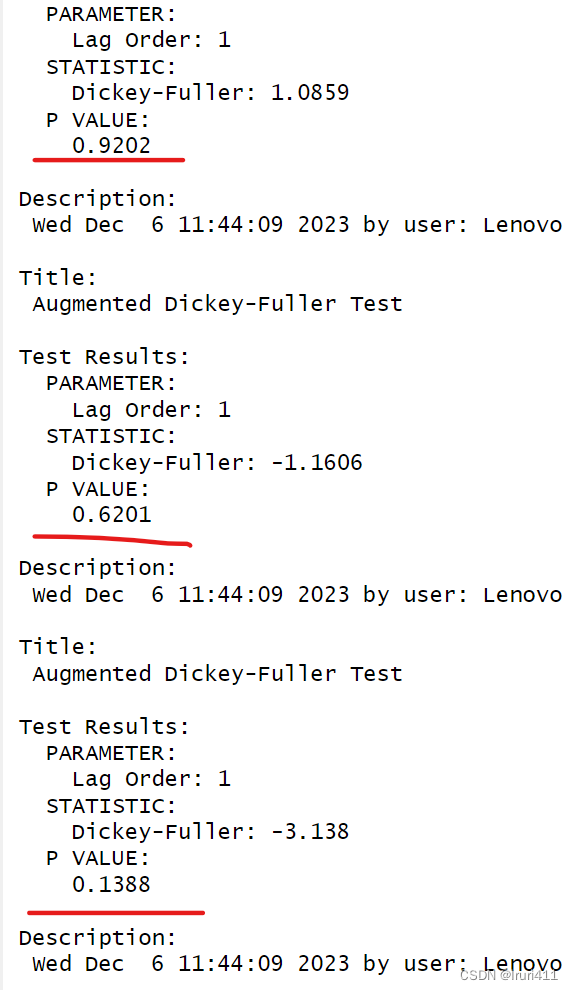
在显著性水平取0.05时，可以认为中国农村居民家庭人均纯收入为非平稳序列。

3.PP检验

原假设	备择假设
$\rho$ =0，序列不平稳	序列平稳

PP检验量可适用于异方差场合的平稳性检验，R软件中可使用urca程序包中的ur.pp( )函数

命令格式如下：adf.test(x,type=,model=,lags=,use.lag=)

该函数的参数说明：

-x:需要进行PP单位根检验的序列名

-type:检验统计量类型。type可以取"Z-alpha"和"Z-tau"两个值

-model:回归模型的类型。model通常可取两个值，model="constant"意味着模型中含有漂移项，而无时间趋势。model=“trend”意味着模型中不含漂移项，而含时间趋势

```{r}
library(urca)
pp.x <- ur.pp(x, type="Z-tau", model="constant", lags="short")
summary(pp.x)
pp.x <- ur.pp(x, type="Z-tau", model="trend", lags="short")
summary(pp.x)
```

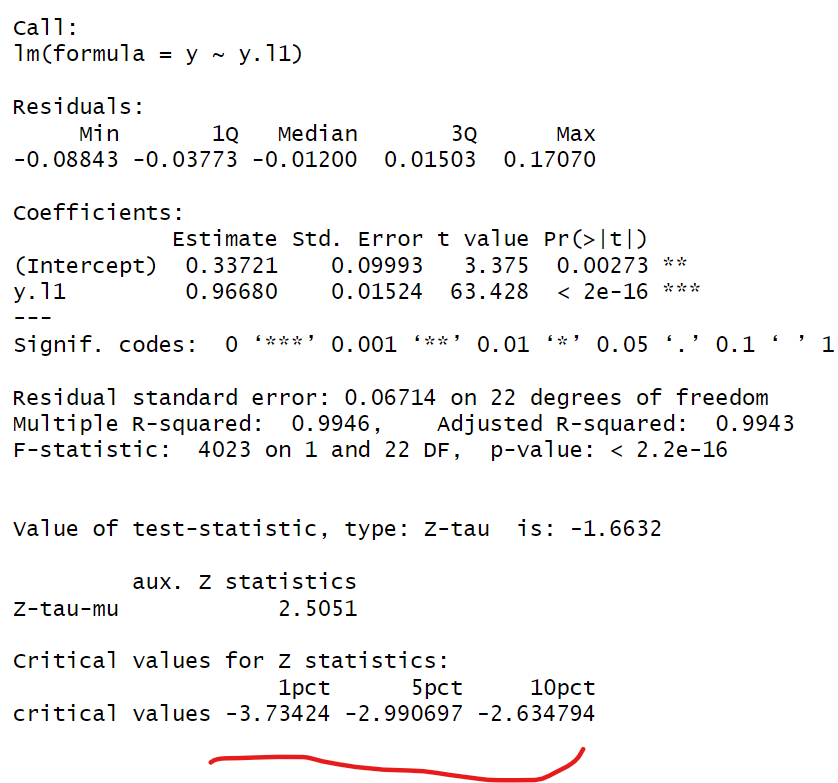
由上图可以看出对应的检验统计量为-1.6632，1%显著性水平下的临界值为-3.73424；5%显著性水平下的临界值为-2.990697；10%显著性水平的临界值为-2.634794，-1.6632>-2.634794，故在10%的显著性水平下可接受原假设，认为该序列不平稳。

4.KPSS检验

上述检验的缺陷在于它们的原假设为"有单位根"，这是因为在数据量不够或者缺乏足够证据时，往往无法拒绝原假设，这时，一些人就觉得应该得到"有单位根"(不平稳)的结论。实际上，只能得到“没有足够证据说明没有单位根”(没有足够证据说平稳)的结论，而不能得到“有证据说不平稳”的结论。KPSS检验最大的特点是它的原假设是序列平稳或趋势平稳，备择假设是序列有单位根。

KPSS检验的原假设和备择假设
原假设	备择假设
序列平稳或趋势平稳	不平稳

在R语言中，urca程序包中的函数ur.kpss( )或程序包tseries中的函数kpss.test( )可进行KPSS检验.函数ur.kpss( )的命令格式如下：

命令格式如下：

ur.kpss(x,type=,lags=,use.lag=)

-x:需要进行PP单位根检验的序列名

-type:检验模型的类型。type可以取"mu"和"tau"两个值.type="mu"意味着检验模型中含有常数项；type="tau"意味着检验模型中含有常数项和时间趋势项

-lags:滞后阶数，可取三个值:lags="short"或"long",表示两个特定阶数。lags="nil"表示无误差修正

-use.lag:使用者自己指定的阶数

```{r}
library(tseries)
kpss.test(x, null = "Level", lshort = TRUE)
kpss.test(x, null = "Trend", lshort = TRUE)
```

p=0.01< $\alpha$ =0.05，拒绝原假设，该序列不平稳。

p=0.1> $\alpha$ =0.05,接受原假设即平稳，这个是趋势平稳也就是说提取趋势后序列平稳，所以和上述结果没有冲突本质上也是不平稳，并且告诉了我们需要提取趋势后平稳。