复习日
仔细回顾一下之前14天的内容,没跟上进度的补一下进度。
作业:
尝试找到一个kaggle或者其他地方的结构化数据集,用之前的内容完成一个全新的项目,这样你也是独立完成了一个专属于自己的项目。
要求:
- 有数据地址的提供数据地址,没有地址的上传网盘贴出地址即可。
- 尽可能与他人不同,优先选择本专业相关数据集
- 探索一下开源数据的网站有哪些?
对于数据的认识,很重要的一点是,很多数据并非是为了某个确定的问题收集的,这也意味着一份数据你可以完成很多不同的研究,自变量、因变量的选取取决于你自己-----很多时候针对现有数据的思考才是真正拉开你与他人差距的最重要因素。
现在可以发现,其实掌握流程后,机器学习项目流程是比较固定的,对于掌握的同学来说,工作量非常少。所以这也是很多论文被懂的认为比较水的原因所在。所以这类研究真正核心的地方集中在以下几点:
- 数据的质量上,是否有好的研究主题但是你这个数据很难获取,所以你这个研究有价值
- 研究问题的选择上,同一个数据你找到了有意思的点,比如更换了因变量,做出了和别人不同的研究问题
- 同一个问题,特征加工上,是否对数据进一步加工得出了新的结论-----你的加工被证明是有意义的。
后续我们会不断给出,在现有框架上,如何加大工作量的思路。
出于设备性能考虑,我这里选用的一个基于低浓度气体下传感器阵列数据分类问题的比较小规模的数据集:Gas sensor array low-concentration - UCI Machine Learning Repository,这个数据集每行代表一个气体样本,前两列是标签信息,第1列:气体类型标签(gas labels);第2列:浓度标签(concentration labels),从第3列开始是传感器响应数据,使用了10种不同的气体传感器,每个传感器贡献900个响应点,所以总共为89行9002列
一、导入数据和读取
import pandas as pd #用于数据处理和分析,可处理表格数据。
import numpy as np #用于数值计算,提供了高效的数组操作。
import matplotlib.pyplot as plt #用于绘制各种类型的图表
import seaborn as sns #基于matplotlib的高级绘图库,能绘制更美观的统计图形。
# 设置中文字体(解决中文显示问题)
plt.rcParams['font.sans-serif'] = ['SimHei'] # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
data = pd.read_csv('gsalc.csv') #读取数据
data.info()
data.isnull().sum() # 没有缺失值,省去缺失值的步骤
说明数据就两列为‘object’类型,其他全是数值型,并且查看数据后发现这两列是标签,该数据集也没有缺失值,所以只需要对连续变量进行处理
二、数据可视化----热力图
所有列全用来热力图肯定不实用,分十个传感器来比较有实践意义
#X = data.iloc[:, 2:].columns.tolist() # 传感器数据(第3列开始)
# 计算变量间的相关系数
#correlation_matrix = data[X].corr()
# 设置图片清晰度,默认值通常是 100,所以设置为 300 会使图像更清晰
#plt.rcParams['figure.dpi'] = 300
# 绘制热力图
#plt.figure(figsize=(12, 10))
#sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
#plt.title('连续变量的热力图')
sensor_names = ['TGS2603','TGS2630','TGS813','TGS822',
'MQ-135','MQ-137','MQ-138','2M012','VOCS-P','2SH12']
plt.figure(figsize=(15,12))
for i, name in enumerate(sensor_names, 1):
plt.subplot(4, 3, i)
# 提取单传感器900个时间点的相关性
sensor_data = data.iloc[:, 2+(i-1)*900 : 2+i*900]
sns.heatmap(sensor_data.corr(),
cmap='coolwarm',
cbar=False,
square=True)
plt.title(f'传感器 {name}')
plt.tight_layout()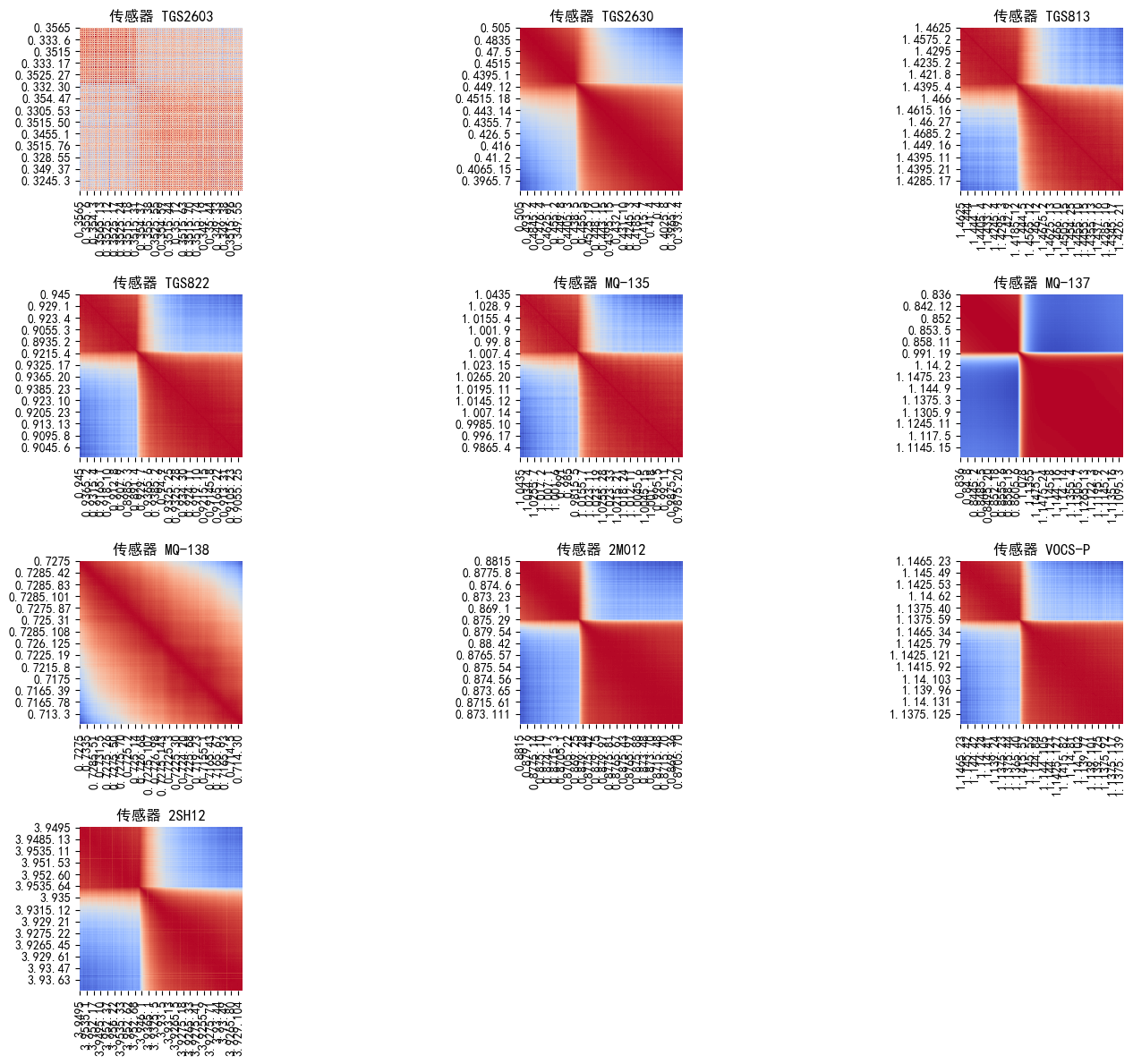
三、变量标准化
根据这个气体传感器数据集的特点,强烈建议进行归一化/标准化处理,原因如下:
- 不同传感器(如TGS系列和MQ系列)的响应范围和量纲可能差异很大
- 9000个特征点跨10种传感器,数值尺度不统一
- 机器学习模型对尺度敏感的算法(如SVM、神经网络等)需要标准化
from sklearn.preprocessing import StandardScaler
# 读取数据(前两列是标签)
data = pd.read_csv('gsalc.csv')
gas_labels = data['ethanol'] # 第1列:气体类型标签
conc_labels = data['100ppb'] # 第2列:浓度标签
sensor_data = data.iloc[:, 2:] # 第3列开始:传感器数据(9000列)
# 标准化处理,分传感器进行
sensor_scaled = np.zeros_like(sensor_data)
for i in range(10): # 10个传感器
start_col = i * 900
end_col = (i + 1) * 900
scaler = StandardScaler()
sensor_scaled[:, start_col:end_col] = scaler.fit_transform(sensor_data.iloc[:, start_col:end_col])
# 重建DataFrame(保留标签列)
processed_data = pd.DataFrame(
sensor_scaled,
columns=[f"feat_{i}" for i in range(sensor_scaled.shape[1])] # 列名可自定义,但这里不改了
)
processed_data.insert(0, 'gas_label', gas_labels)
processed_data.insert(1, 'concentration', conc_labels)
# 检查第一个传感器标准化后的均值和方差
print("均值:", np.mean(sensor_scaled[:, :900]), "(应接近0)")
print("方差:", np.std(sensor_scaled[:, :900]), "(应接近1)")
# ---------结果如下----------
均值: 1.1354490658838055e-16 (应接近0)
方差: 1.0 (应接近1)# 原始数据 vs 标准化后数据(以第一个传感器为例)
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(sensor_data.iloc[0, :900]) # 第一个样本的原始数据
plt.title("TGS2603 原始数据")
plt.subplot(1, 2, 2)
plt.plot(sensor_scaled[0, :900]) # 标准化后
plt.title("标准化后")
plt.show()
四、划分数据集
from sklearn.model_selection import train_test_split
# 使用标准化后的数据(processed_data),特征:从第3列开始的所有传感器数据(已标准化)
X = processed_data.drop(['gas_label', 'concentration'], axis=1) # 特征,axis=1表示按列删除
# 标签:第1列是气体类型,第2列是浓度(根据任务目标二选一)
y_gas = processed_data['gas_label'] # 气体分类任务
y_conc = processed_data['concentration'] # 浓度回归任务
# 划分数据集(以气体分类为例)
X_train, X_test, y_train, y_test = train_test_split(X, y_gas,
test_size=0.2, # 20%测试集
random_state=42, # 随机种子
stratify=y_gas # 保持气体类别分布一致
)五、训练预测
先不调参
# 数据进入机器学习模型训练预测
from sklearn.ensemble import RandomForestClassifier #随机森林分类器
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score # 用于评估分类器性能的指标
from sklearn.metrics import classification_report, confusion_matrix #用于生成分类报告和混淆矩阵
import warnings #用于忽略警告信息
warnings.filterwarnings("ignore") # 忽略所有警告信息
# --- 1. 默认参数的随机森林 ---
print("--- 1. 默认参数随机森林 (训练集 -> 测试集) ---")
import time # 这里介绍一个新的库,time库,主要用于时间相关的操作,因为调参需要很长时间,记录下会帮助后人知道大概的时长
start_time = time.time() # 记录开始时间
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train) # 在训练集上训练
rf_pred = rf_model.predict(X_test) # 在测试集上预测
end_time = time.time() # 记录结束时间
print(f"训练与预测耗时: {end_time - start_time:.4f} 秒")
print("\n默认随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred))
print("默认随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred))
用贝叶斯优化进行调参,选用三折交叉验证(算力不行就少点吧
from skopt import BayesSearchCV
from skopt.space import Integer # 定义整数型参数空间(如 n_estimators 的取值范围)
# 定义要搜索的参数空间
search_space = {
'n_estimators': Integer(50, 200), # 树数量
'max_depth': Integer(3, 15), # 最大深度
'min_samples_split': Integer(2, 10), # 分裂最小样本数
'min_samples_leaf': Integer(1, 5) # 叶节点最小样本数
}
# 创建贝叶斯优化搜索对象
bayes_search = BayesSearchCV(
estimator=RandomForestClassifier(random_state=42),
search_spaces=search_space,
n_iter=32, # 迭代次数,值越大效果越好但耗时越长,可根据需要调整
cv=3, # 3折交叉验证,这个参数是必须的,不能设置为1,否则就是在训练集上做预测了
n_jobs=-1,
scoring='accuracy'
)
start_time = time.time()
# 在训练集上进行贝叶斯优化搜索
bayes_search.fit(X_train, y_train)
end_time = time.time()
print(f"贝叶斯优化耗时: {end_time - start_time:.4f} 秒")
print("最佳参数: ", bayes_search.best_params_)
# 使用最佳参数的模型进行预测
best_model = bayes_search.best_estimator_
best_pred = best_model.predict(X_test)
print("\n贝叶斯优化后的随机森林 在测试集上的分类报告:")
print(classification_report(y_test, best_pred))
print("贝叶斯优化后的随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, best_pred))

六、SHAP库可视化
有点麻烦的是数据维度太高了,要采样来计算shap值
import shap
# 创建 SHAP 解释器,用优化后的随机森林
explainer = shap.TreeExplainer(bayes_search.best_estimator_)
# 计算 SHAP 值(基于测试集)
# 由于数据维度过高,随机选取测试样本和100个代表性特征
sample_idx = np.random.choice(X_test.shape[0], min(50, X_test.shape[0]), replace=False)
feature_idx = np.random.choice(X_test.shape[1], 100, replace=False) # 随机选100个特征和样本
shap_values = explainer.shap_values(X_test.iloc[sample_idx, feature_idx]) # 返回长度为2的列表(对应二分类),这个计算很耗时
# 搞清楚数据维度
print("shap_values shape:", shap_values.shape)
print("shap_values[0] shape:", shap_values[0].shape) # 表示第一个样本的SHAP值,形状为(特征数量,2)
print("shap_values[:, :, 0] shape:", shap_values[:, :, 0].shape) # 这里使用了切片操作 [:, :, 0],意味着选取所有样本、所有特征在第三维上索引为0的元素,即分类为0
print("X_test shape:", X_test.shape)图就不想画了

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








