密码学归约证明——基于伪随机函数的消息鉴别码方案

皮皮罴

已于 2022-12-23 17:40:45 修改

阅读量295

点赞数

分类专栏：现代密码学文章标签：密码学安全

于 2022-12-23 17:38:40 首次发布

本文链接：https://blog.csdn.net/weixin_65617488/article/details/128421346

版权

现代密码学专栏收录该内容

9 篇文章 3 订阅

订阅专栏

1. 消息鉴别码实验 $Macforge_{A,\Pi }\left ( n \right )$

运行 $Gen\left ( 1^{n} \right )$ 得到密钥 $k$ ，即 $k\leftarrow Gen(1^n)$ 。

敌手 $A$ 获得输入 $1^n$ ，且能够访问预言机 $Mac$ ，最终输出 $(m,t)$ ，其中 $t$ 为消息 $m$ 的鉴别码。设 $Q$ 为敌手 $A$ 访问预言机 $Mac$ 的问询集合。

当且仅当 $Vrfy_k(m,t)=1$ 且 $m \notin Q$ ，实验输出1。其中 $Vrfy$ 是鉴别码方案的验证方法。

如果一个消息鉴别码 $MAC$ 方案，满足 $\forall PPT$ 敌手，存在可忽略函数 $negl(n)$ ，使实验 $Pr[Mac-forge_{A,\Pi} (n)=1]\leq negl(n)$ ，我们称其为适应性选择消息攻击下存在性不可伪造的，即 $CMA$ 安全的。

2. 伪随机函数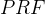 $PRF$

令 $\large F:\left \{ 0,1 \right \}^{*}\times \left \{ 0,1 \right \}^{*}\rightarrow \left \{ 0,1 \right \}^{*}$ 是有效的、长度保留的、带密钥的函数。如果对于所有多项式时间的区分器 $\large D$ ，存在可忽略函数 $negl(n)$ ，满足

$\large \left | Pr\left [ D^{F_{k}\left ( \cdot \right )}\left ( 1^{n} \right )=1 \right ] -Pr\left [ D^{f\left ( \cdot \right )}\left ( 1^{n} \right )=1 \right ]\right |\leq negl\left ( n \right )$

则 $\large F$ 是一个伪随机函数，其中 $\large k\leftarrow \left \{ 0,1 \right \}^{n}$ 是随机均匀选择的， $\large f\left ( \cdot \right )$ 是将 $\large n$ 比特字符串映射到 $\large n$ 比特字符串的函数集合中均匀随机选择出来的。

这部分在《密码学归约证明——选择明文攻击下的不可区分性》中已经有所描述。

3. 基于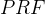 $PRF$ 的 $CMA$ 安全的消息鉴别码方案

$Gen$ ：输入参数 $1^n$ ，均匀随机选择 $k\leftarrow {\{0,1\}}^n$ ；
$Mac$ ：输入密钥 $k$ 和消息 $m \in {\{0,1\}}^n$ ，输出标记 $t:=F_k(m)$ 。
$Vrfy$ ：输入密钥 $k$ 、消息 $m$ 和标记 $t \in {\{0,1\}}^n$ ，当且仅当 $t=F_k(m)$ 时输出1。

此方案我们只考虑密钥、消息和标记的长度相同的情况（即长度保留）。因此，倘若 $Mac$ 接收到长度不为 $n$ 的消息 $m$ ，则不输出； $Vrfy$ 接收到长度不为 $n$ 的标记，输出0。

4. 适应性选择消息攻击下存在性不可伪造

若 $F$ 是一个 $PRF$ ，则上述构造方案 $\Pi$ 是长度为 $n$ 的定长消息的 $CMA$ 安全的 $MAC$ 方案。

思路类似于之前的归约证明方式，定义一个区分器 $D$ 可以区分随机函数与 $PRF$ ，将此区分器归约到攻破上述 $MAC$ 方案。

假设一个消息鉴别码方案 $\Pi'=(Gen',Mac',Vrfy')$ 是将上述 $MAC$ 方案中的 $PRF$ 替换为随机函数的变体 $MAC$ 。因此在此种情况下，敌手 $A$ 可以认为 $m$ 是均匀分布在 $\{0,1\}^n$ 上的，因此 $Pr[Macforge_{A,\Pi'}(n)=1]\leq \frac{1}{2^n}$ 。

现在构造区分器 $D$ ，目标是区分 $PRF$ 与随机函数 $f$ ：区分器 $D$ 给定输入 $1^n$ ，并且可以访问预言机 $O:\{0,1\}^n\rightarrow \{0,1\}^n$ ：

运行 $A(1^n)$ 。当敌手 $A$ 向其 $MAC$ 预言机问询消息 $m$ 时，区分器 $D$ 向 $O$ 问询并得到应答 $t$ ，返回给 $A$ 。
$A$ 最终输出 $(m,t)$ ：区分器 $D$ 向 $O$ 问询并得到应答 $t'$ ，若 $t'=t$ 且 $A$ 从未问询过 $m$ ，则区分器输出1。