数字图像处理中的傅里叶变换

一、文章简介

当我们谈论数字图像处理和信号处理时，傅里叶变换是一个不可忽视的重要概念。它为我们提供了一种强大的工具，能够深入理解数字信号和图像的内在结构。或许对于初次接触这个领域的同学来说，傅里叶变换可能显得有些抽象，但正是这个变换让我们能够在数字处理的世界中发现隐藏在信号背后的奥秘。

• 本文不会讲述晦涩难懂的数学原理 ，而是期望以一种直观感受的形式尝试去解析傅里叶变换的核心概念，并探讨其在数字图像处理中的重要性。
• 无论是否有过相关经验，我们将以简明易懂的方式探讨傅里叶变换的基础原理，帮助同学们建立起对这一概念的认识。通过本文，我们旨在让每一位读者都能够轻松理解傅里叶变换的背后逻辑，并在数字图像处理的旅程中更加得心应手。让我们一同踏上这段有趣而富有挑战的学习之旅吧！

二、先直观理解傅里叶变换

许多教学资源上讨论的都是时域和频率域的关系，例如下面的图片：





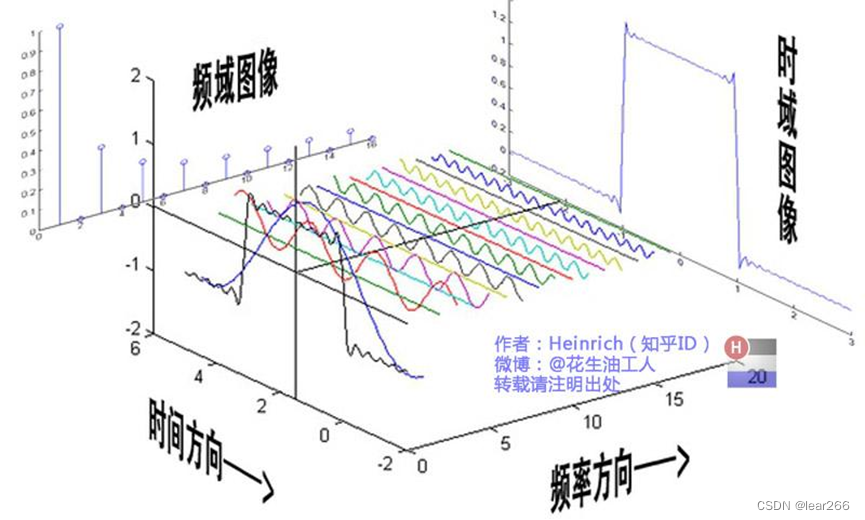
但在数字图像处理领域，我们讨论的是空间域与频率域的关系。啥是空间域，简单来说就是一张图像（为了方便解释，这里都用灰度图像）

（没错又是我lena）

就一张图像哪来的什么频率呢？别着急，咱慢慢来。
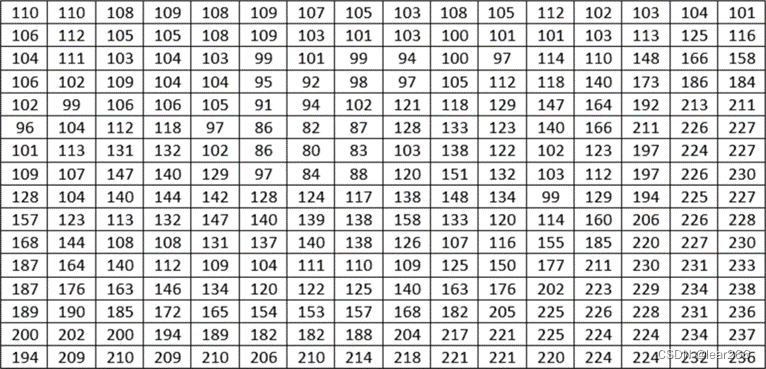
计算机里的图像，本质上就是由一个个像素方块组成，而每个像素方块有它对应的灰度值（不理解没关系，可以简单认为灰度值就代表了颜色，黑色取值为0，白色取值为255，然后从黑到白中间的深灰色、灰色、浅灰色……都有它对应的0~255中间的取值）。这样看，这张图像在计算机里面就是一个矩阵（lena图片某个部分的像素值）：



这也没有什么频率啊？不着急，咱们从一个3d的视角看这样的图像矩阵：



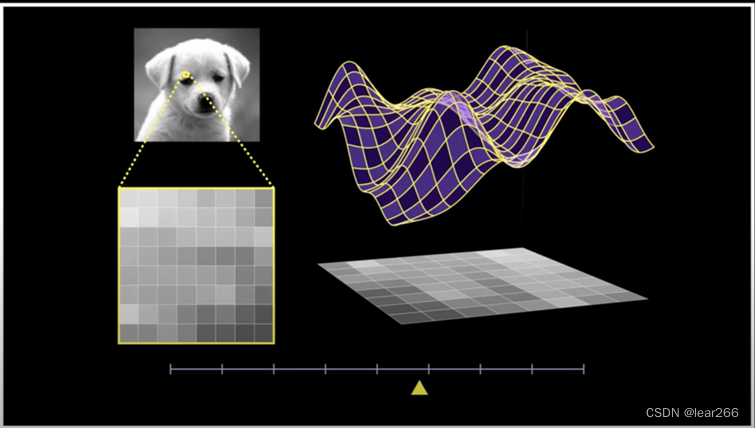
然后我们再分别以图像的x轴、y轴（或者说矩阵的第一维和第二维）为横轴，以灰度值为纵轴，这样就可以得到两个函数，分别表示灰度值在x轴和y轴的变化情况，如下图：

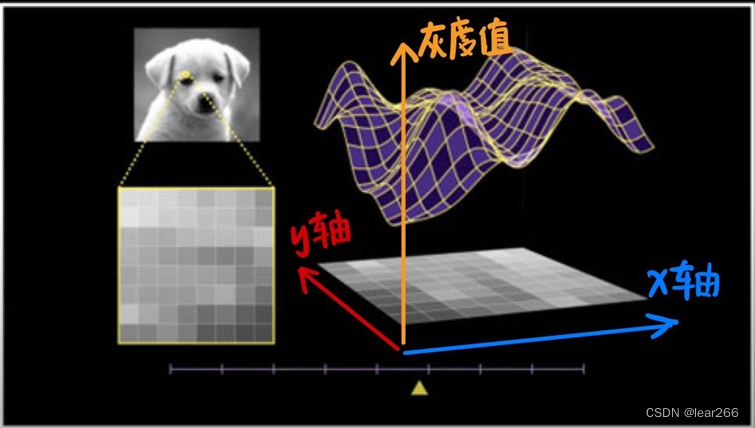
这个图片上某一点的灰度值是一个关于x和y的函数，我们记作$f(x,y)$，那么想要求$f(x,y)$与x的关系（或者说关于x的边缘分布），就要让$f(x,y)$对y进行积分，有$g(x)={\int }_{-\infty }^{\infty }f(x,y)dy$，求$f(x,y)$与y的关系也是同理：$h(y)={\int }_{-\infty }^{\infty }f(x,y)dx$


我们把灰度值叫做z轴，那么我们现在y-z平面和x-z平面上分别有一个函数h(y)和g(x)，接下来应该如何做呢？想想我们在时域时，通过傅里叶变换，将其转化到频率域（没关系，先记着这里有个傅里叶变换，原理我们后面再介绍），简单来说就是做了下面的变换：

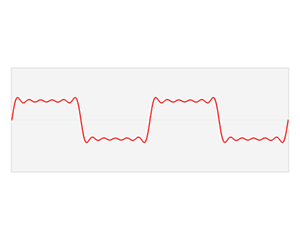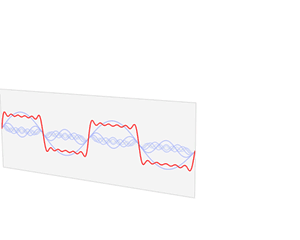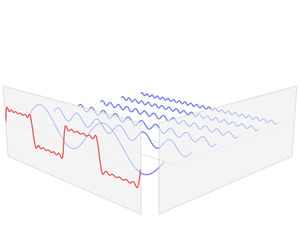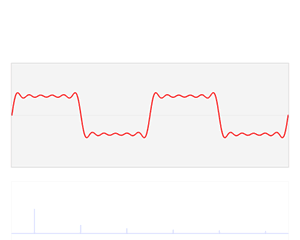
也就是上面贴过的图：

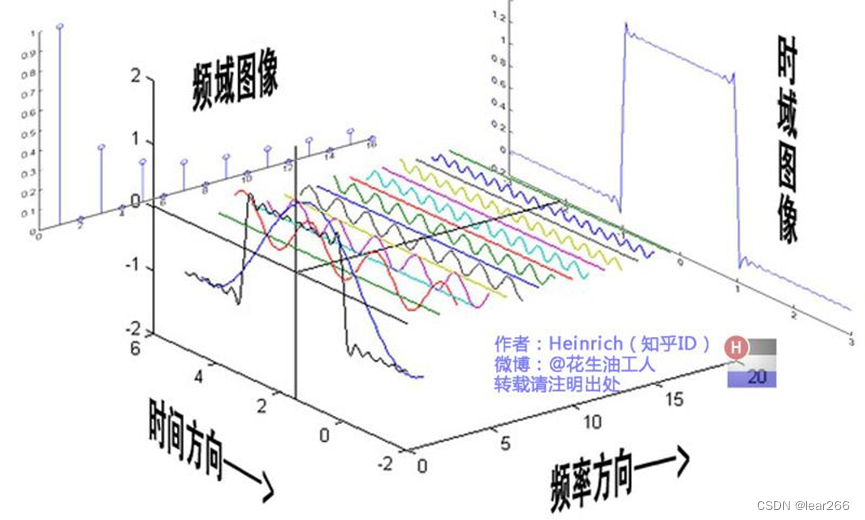
（这里还埋了一个小坑，所有连续的函数都可以由一堆正弦和余弦函数表示，没关系，先记着有这样一个东西）


现在我们把y-z平面和x-z平面上的函数h(y)和g(x)都做这样的变换，分别映射到了v-k平面和u-k平面，在这里k就是振幅，而v和u是我们任意起的一个符号，现在，我们已经进入频率空间了。


还记得y-z平面和x-z平面实际上都是脱胎于一张图像吗：

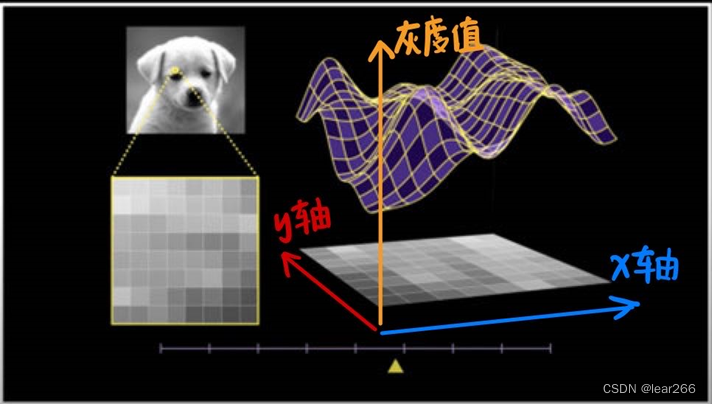
那咱们也把v-k平面和u-k平面组合成一张图像，以u-v为轴，并且将k映射到灰度值，即k越大，对应的那一点越亮。于是乎，我们终于由原来的x-y轴图像变换到了u-v频率图像，从空间域变换到了频率域

（右边是原图，左边是傅里叶变换之后的图片）

对于左边的那张频率图，没有什么物理意义是我们肉眼能看出来的，但是仍然是有一些能辅助我们理解的地方：

• 左边图像的每个点与右边图像的每个点不存在对应关系
• 左边图像上的某个点(u,v)，其实是代表了一个信号$f(x)=Asin(f_{0}x+\theta )$（这个配合后面的公式理解）
• 左边图像中间代表低频信号，越向外越代表高频信号（即频率是和点的位置相关的）

三、离散傅里叶变换公式

（数学公式轰炸警告⚠）
不想听数学的同学可以跳过这一节了，想了解一下的同学可以接着往下看。

先说结论：
原图像 --------------DFT------------------------>
<---------------------IDFT-----------------频率图像

1. 二维离散傅里叶变换（Discrete Fourier Transform，DFT）
   $F(u,v)={\sum }_{x=0}^{M-1}{\sum }_{y=0}^{N-1}f(x,y)\cdot e^{-i2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right),}$
   $u=0,1,...,M-1,v=0,1,...,N-1$
   
   这个公式的作用是将一张图片变换到频率域

2. 二维逆离散傅里叶变换（IDFT）
   $f(x,y)=\frac{1}{MN}{\sum }_{x=0}^{M-1}{\sum }_{y=0}^{N-1}F(u,v)\cdot e^{i2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right),}$
   $x=0,1,...,M-1,y=0,1,...,N-1$
   
   这个公式的作用是将图片的频率域表示变换回一张图片

这样我们就可以理解上面的频域图像中的某一点具有什么含义了：

首先，每一个点的函数值$F(u,v)$都存在实部Re和虚部Im，这就有了以下振幅A和相位P的公式：
$A(u,v)=\sqrt{\text{Re}(F(u,v){)}^2+\text{Im}(F(u,v){)}^2}$
$P(u,v)=\arctan 2\left(\text{Im}(F(u,v)),\text{Re}(F(u,v))\right)$

这样我们就知道频率域图像中的每一点(u,v)都代表了某个频率的信号，而且能定性知道这个信号的振幅是大还是小。知道振幅其实就是知道这个频率的信号的占比是多少，振幅越大就是占比越多。比如下图，频率域图像中间部分比较亮，所以就是低频信号占比较多。

接下来是公式的理解和推导时间

傅里叶级数

傅里叶告诉我们：任何周期函数都可以表示为不同频率的正弦函数和/或余弦函数加权之和。
直观的感受：

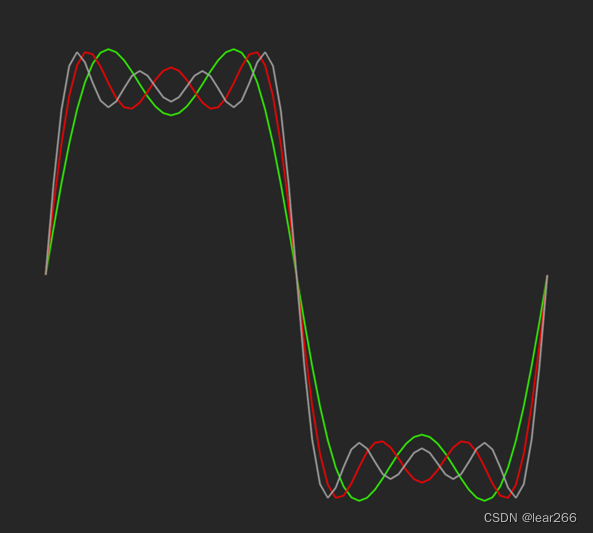
我们可以从线性代数的层面上去理解。
①首先，当我们有了空间中的一组正交基{$q_1,q_2,q_3\dots$}后，我们可以把空间中的任意向量表示为这组基的线性组合：
$v=x_1{q}_1+x_2{q}_2+...+x_n{q}_n$

②而当我们想要求得系数x1时，可以利用正交基的性质（$q_1{q}_1^T=1,q_1{q}_2=0,...,q_1{q}_n=0$）求得：$q_1^{T}v=x_1$,同理对其他的也有$q_i^{T}v=x_i$

③现在我们把{$1，sinx，cosx，sin2x，cos2x\dots$}看作空间的正交基{$q_1,q_2,q_3\dots$},· 对于该空间的向量或者说函数，表示为这组基的线性组合，为方便这里的系数分别用an与bn表示：
$f(x)=\frac{a_0}{2}+b_{1}sinx+a_{1}cosx+b_{2}sin2x+a_{2}cos2x+\dots$
即为：
$f(x)=\frac{a_0}{2}+{\sum }_{n=1}^{\infty }{a}_{n}cos(nx)+b_{n}sin(nx)$

④接下来我们想求这组基的系数$a_0,b_n,a_n$，该怎么做呢？与上面一样，利用正交基的性质！
对$a_n$有：
$f(x)cos(nx)=\frac{a_0}{2}cos(nx)+({\sum }_{n=1}^{\infty }{a}_{n}cos(nx)+b_{n}sin(nx))cos(nx)$
两边同时求积分：
${\int }_{-\pi }^{\pi }f(x)cos(nx)dx={\int }_{-\pi }^{\pi }{a}_{n}cos(nx)cos(nx)dx$
由于基之间的正交性质，只剩下$a_n$:
${\int }_{-\pi }^{\pi }f(x)cos(nx)dx={\int }_{-\pi }^{\pi }{a}_n\frac{cos(2nx+1)}{2}dx$,
解得：
$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)cos(nx)dx$,
同理有：
$a_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }f(x)dx$
$b_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)sin(nx)dx$，

这就是傅里叶级数。
傅里叶级数可以解决周期函数的问题，那么非周期函数应该如何解决呢？
别急，这就轮到我们大名鼎鼎的傅里叶变换出场了！

傅里叶变换

傅里叶还告诉我们：非周期函数也可以表示为不同频率的正弦函数和/或余弦函数的加权积分。
即：
$f(x)={\int }_{-\infty }^{\infty }(a_{w}sin(wx)+b_{w}cos(wx))dw$，
此外，欧拉还告诉我们：
$e^{i\psi }=cos\psi +isin\psi$，
所以：
$cos\psi =\frac{e^{i\psi }+e^{-i\psi }}{2}$
$sin\psi =\frac{e^{i\psi }-e^{-i\psi }}{2}$，
也就是说：
$cos(wx)=\frac{e^{iwx}+e^{-iwx}}{2}$
$sin(wx)=\frac{e^{iwx}-e^{-iwx}}{2}$，
那么就有：
$f(x)={\int }_{-\infty }^{\infty }(c_w{e}^{iwx})dw$,
其中$c_w$是与$a_w$和$b_w$相关的系数，
令$2\pi \mu =w$，
同时令$c_w=F(\mu )$，
则有$f(x)={\int }_{-\infty }^{\infty }(F(\mu )e^{i2\pi \mu x})d\mu$，
于是，我们成功把f(x)用频率域的函数F(μ)来表示，我们称这个式子为傅里叶反变换(频率域->时域)。
当我们想要从时域转化到频率域，也就是说想要求出F(μ)时，应该怎么做呢？
还记得我们当时是如何求出基的系数吗？没错，通过同样的操作我们也可以求出在这冲情况下的基的系数（也就是F(μ)）：
$F(\mu )={\int }_{-\infty }^{\infty }(f(x)e^{-i2\pi \mu x})dx$,
我们称之为傅里叶变换(时域->频率域)

离散傅里叶变换

当你来到这，恭喜你，最烧脑的地方已经结束了 ，但是还有一些问题：图像可是离散的（表示为一个个像素点），我要怎么对一个离散的东西求傅里叶变换？
简单，把积分变成求和就行了：
$F(\mu )={\sum }_{-\infty }^{\infty }(f(x)e^{-i2\pi \mu x})$
$f(x)={\sum }_{-\infty }^{\infty }(F(\mu )e^{i2\pi \mu x})$

但是但是，图像不仅是离散的，还是二维的，应该怎么办？
答案是，对两个维度都求和，就得到了我们上面出现过的式子：
DFT
$F(u,v)={\sum }_{x=0}^{M-1}{\sum }_{y=0}^{N-1}f(x,y)\cdot e^{-i2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right),}$
IDFT
$f(x,y)=\frac{1}{MN}{\sum }_{x=0}^{M-1}{\sum }_{y=0}^{N-1}F(u,v)\cdot e^{i2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right),}$

快速傅里叶变换

FFT（Fast Fourier Transformation），是一种对离散傅里叶变换的加速算法，要了解这个算法，首先要做一些前置知识的准备。

多项式的两种表示

①系数表示法
$f(x)=a_0+a_{1}x+a_2{x}^2+....+a_n{x}^n$，由于基是定好的，那么在知道了$a_0,a_1,...,a_n$后，我们就能够确定$f(x)$，即将$f(x)$用{$a_0,a_1,...,a_n$}进行表示

②点值表示法
$f(x)=a_0+a_{1}x+a_2{x}^2+....+a_n{x}^n$，在给定了n个满足函数的点后，也能够确定$f(x)$，所以可以将$f(x)$表示为{$(x_0,f(x_0)),(x_1,f(x_1)),...,(x_n,f(x_n))$}

多项式相乘

当我们求$f(x)g(x)$的时候，可以用上述的两种方式。
如果使用系数表示法，复杂度是$O(n^2)$，因为$f(x)$的每一个系数都要和$g(x)$的每个系数做乘法，从而得到新的系数。
如果使用点值表示法，复杂度可以是$O(n)$，因为当我们对两个多项式都取一样的{$x_0,..,x_n$}的时候，求$f(x)g(x)$只要n个点对应的函数值相乘就行。
所以多项式相乘时，我们可以使用点值表示法来进行一定的加速。

单位根

以单位圆点为起点，单位圆的n等分点为终点，在单位圆上可以得到n个复数，设幅角为正且最小的复数为$w_n^0$

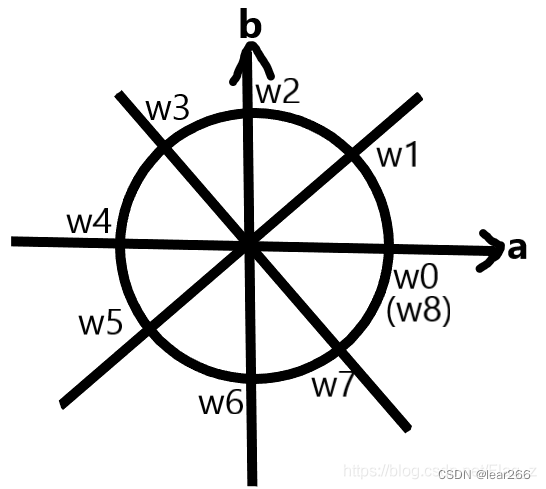
我们可以看到$w_n^k$对应的点为$(cos\frac{k}{n}2\pi ,sin\frac{k}{n}2\pi )$，即对应着复数$cos\frac{k}{n}2\pi +isin\frac{k}{n}2\pi$

单位根的性质

1. $(w_n^1{)}^k=w_n^k$
2. $w_n^k=w_{2n}^{2k}$
3. $w_n^k=-w_n^{k+\frac{n}{2}}$
4. $w_n^0=w_n^n=1$

FFT的推导

对于$f(x)=a_0+a_{1}x+a_2{x}^2+...,a_{n-1}{x}_{n-1}$，我们都可以假设$n=2^s$，因为即使$f(x)$的项数没有刚好为2的整数次幂，也可以在后面补零，使得项数为$2^s$。

然后按照$a_i$下标的奇偶性将$f(x)$拆分成两部分：
$f(x)=(a_0+a_2{x}^2+a_4{x}^4+...+a_{n-2}{x}^{n-2})+(a_{1}x+a_3{x}^3+a_5{x}^5+...+a_{n-1}{x}^{n-1})$，
令：
$f_1(x)=a_0+a_{2}x+a_4{x}^2+...+a_{n-2}{x}^{\frac{n}{2}-1}$
$f_2(x)=a_1+a_{3}x+a_5{x}^2+...+a_{n-1}{x}^{\frac{n}{2}-1}$，

则$f(x)=f_1(x^2)+x{f}_2(x^2)$

然后我们使用点值表示，所取的点就是上面介绍的单位根
带入$x=w_n^k$，有：
$$\begin{gathered} f(w_n^k)=f_1(w_n^{2k})+w_n^k{f}_2(w_n^{2k}) \\ =f_1(w_{\frac{n}{2}}^k)+w_n^k{f}_2(w_{\frac{n}{2}}^k) \end{gathered}$$，
带入$x=w_n^{k+\frac{n}{2}}$,有：
$$\begin{gathered} f(w_n^{k+\frac{n}{2}})=f_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}{f}_2(w_n^{2k+n}) \\ =f_1(w_{\frac{n}{2}}^k)-w_n^k{f}_2(w_{\frac{n}{2}}^k) \end{gathered}$$


这样，我们在求出$f_1(w_{\frac{n}{2}}^k)$和$f_2(w_{\frac{n}{2}}^k)$后，就能$O(1)$地求出$f(w_n^{k+\frac{n}{2}})$和$f(w_n^k)$，而要求出$f_1(w_{\frac{n}{2}}^k)$和$f_2(w_{\frac{n}{2}}^k)$,就要求出$f_1(w_{\frac{n}{4}}^k)$和$f_2(w_{\frac{n}{4}}^k)$，…，这样就转化为了一个分治的过程。

所以我们可以以$O(logn)$求出$f_1(w_{\frac{n}{2}}^k)$和$f_2(w_{\frac{n}{2}}^k)$，进而可以以$O(nlogn)$求出所有的$f(w_n^k)$

而反观我们的离散傅里叶变换$F(u,v)={\sum }_{x=0}^{M-1}{\sum }_{y=0}^{N-1}f(x,y)\cdot e^{-j2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right),}$，其实也是这样一个函数相乘的过程，所以可以通过这个原理进行加速。

代码实现

OpenCV实现FFT
OpenCV实现DFT

四、傅里叶变换在数字图像处理中的应用

频谱分析

既然知道了频率图像的每一部分都对应着原图像的某些部分，那么我们常常可以通过频域分析信号中不同频率的成分，并进行相应的操作，比如说：

1. 频谱可视化：傅里叶变换可以将信号分解为不同频率的分量，形成频谱图。通过分析频谱图，我们可以清晰地看到信号中哪些频率的成分占主导地位，帮助我们理解信号的频率结构。

2. 滤波器设计：在频谱分析中，我们可以设计各种滤波器，如低通、高通、带通和带阻滤波器，以选择或排除特定频率范围内的信号成分。这对于信号处理、通信系统和音频处理等领域非常重要。

3. 信号去噪：通过傅里叶变换，我们可以将信号分解为频域中的成分。在频域中，我们可以过滤掉噪声或不需要的成分，然后通过逆傅里叶变换将处理后的信号还原到时域。

4. 频域分析：傅里叶变换使得信号在频域中的分析变得更加方便。例如，我们可以通过分析频率域中的谱峰来估计信号的主要频率，或者通过计算谱宽来了解信号的频率分布。

而以下则是具体场景的应用：

图像处理

假如我在空间中取得了一张照片，但是因为射线的原因导致了噪音，请问我应该如何去除噪音呢？
直接上代码：
陷波滤波器

五、参考文章

超详细易懂FFT（快速傅里叶变换）及代码实现
快速傅里叶变换（FFT）超详解
直观理解傅里叶分析及在图像上的应用
傅里叶变换