Atcoder Beginner Contest 309——D-F讲解

前言

由于最近期末考试，所以之前几场都没打，给大家带了不便，非常抱歉。

这个暑假，我将会持续更新，并给大家带了更好理解的题解！希望大家多多支持。

由于，$A\sim C$ 题比较简单，所以就不写了，如果大家有不会的，可以私信问我。

---

D - Add One Edge

1. Description

Problem Statement

We have an undirected graph with $(N_1+N_2)$ vertices and $M$ edges. For $i=1,2,\dots ,M$, the $i$-th edge connects vertex $a_i$ and vertex $b_i$.

The following properties are guaranteed:
Vertex $u$ and vertex $v$ are connected, for all integers $u$ and $v$ with $1\le u,v\le N_1$.
Vertex $u$ and vertex $v$ are connected, for all integers $u$ and $v$ with $N_1+1\le u,v\le N_1+N_2$.
Vertex $1$ and vertex $(N_1+N_2)$ are disconnected.
Consider performing the following operation exactly once:
choose an integer $u$ with $1\le u\le N_1$ and an integer $v$ with $N_1+1\le v\le N_1+N_2$, and add an edge connecting vertex $u$ and vertex $v$.
We can show that vertex $1$ and vertex $(N_1+N_2)$ are always connected in the resulting graph; so let $d$ be the minimum length (number of edges) of a path between vertex $1$ and vertex $(N_1+N_2)$.
Find the maximum possible $d$ resulting from adding an appropriate edge to add.

Definition of "connected" Two vertices $u$ and $v$ of an undirected graph are said to be connected if and only if there is a path between vertex $u$ and vertex $v$. ### Constraints

$1\le N_1,N_2\le 1.5\times 10^5$
$0\le M\le 3\times 10^5$
$1\le a_i\le b_i\le N_1+N_2$
$(a_i,b_i)\ne (a_j,b_j)$ if $i\ne j$.
Vertex $u$ and vertex $v$ are connected for all integers $u$ and $v$ such that $1\le u,v\le N_1$.
Vertex $u$ and vertex $v$ are connected for all integers $u$ and $v$ such that $N_1+1\le u,v\le N_1+N_2$.
Vertex $1$ and vertex $(N_1+N_2)$ are disconnected.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N_1$ $N_2$ $M$
$a_1$ $b_1$
$⋮$
$a_M$ $b_M$

Output

Print the answer.

Sample Input 1

3 4 6
1 2
2 3
4 5
4 6
1 3
6 7

Sample Output 1

5

If we set $u=2$ and $v=5$, the operation yields $d=5$, which is the maximum possible.

Sample Input 2

7 5 20
10 11
4 5
10 12
1 2
1 5
5 6
2 4
3 5
9 10
2 5
1 4
11 12
9 12
8 9
5 7
3 7
3 6
3 4
8 12
9 11

Sample Output 2

4

---

2. Solution

根据这个图以及题目大意，可以看出题目中所给的无向图一定是分成了两个连通块，并且起点 $1$，终点 $N_1+N_2$一定不再同一个连通块内部。

（1）对于连通块 $1$，我们只需计算起点 $1$ 到连通块内各个顶点的最短距离，取出最长的距离 $re{s}_1$。
（2）对于连通块 $2$，我们只需计算终点 $N_1+N_2$ 到连通块内各个顶点的最短距离，取出最长的距离 $re{s}_2$。

最后的答案就是 $re{s}_1+re{s}_2+1$，因为我们中间还要加一条边，所以距离还会多 $1$。

---

3.Code

#include <iostream>
#include <cstring>
#include <queue>
#include <vector>

using namespace std;

const int N = 3e5 +10;

int n1, n2, m;
int u, v;
vector<int> g[N];
int dist[N], st[N];

void bfs(int start) //模版（不多说了，不会的可以问我）
{
	memset(dist, 0x3f, sizeof dist);
	memset(st, 0, sizeof st);
	queue<int> q;
	q.push(start);
	dist[start] = 0;
	
	while (q.size())
	{
		auto t = q.front();
		q.pop();
		
		if (st[t]) continue;
		st[t] = 1;
		
		for (auto c : g[t])
			q.push(c), dist[c] = min(dist[c], dist[t] + 1);
	}
}

int main()
{
	cin >> n1 >> n2 >> m;
	
	while (m --)
	{
		cin >> u >> v;
		g[u].push_back(v), g[v].push_back(u);
	}
	
	bfs(1); //求连通块1内点1到其他点的最短距离
	int res1 = 0;
	for (int i = 1; i <= n1; i ++)
		res1 = max(res1, dist[i]);//取出到所有点中最短距离中最长的
		
	bfs(n1 + n2);//求连通块2内点N1+N2到其他点的最短距离
	int res2 = 0;
	for (int i = n1 + 1; i <= n1 + n2; i ++)
		res2 = max(res2, dist[i]); //取出到所有点中最短距离中最长的
		
	cout << res1 + res2 + 1 << endl;
	
	return 0;
}

4. Time Complexity: $O(N_1+N_2)$

---

E - Family and Insurance

1.Description

Problem Statement

There is a family consisting of person $1$, person $2$, $\dots$, and person $N$. For $i\ge 2$, person $i$’s parent is person $p_i$.
They bought insurance $M$ times. For $i=1,2,\dots ,M$, person $x_i$ bought the $i$-th insurance, which covers that person and their descendants in the next $y_i$ generations.
How many people are covered by at least one insurance?

Constraints

$2\le N\le 3\times 10^5$
$1\le M\le 3\times 10^5$
$1\le p_i\le i-1$
$1\le x_i\le N$
$1\le y_i\le 3\times 10^5$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$ $M$
$p_2$ $\dots$ $p_N$
$x_1$ $y_1$
$⋮$
$x_M$ $y_M$

Output

Print the answer.

Sample Input 1

7 3
1 2 1 3 3 3
1 1
1 2
4 3

Sample Output 1

4

The $1$-st insurance covers people $1$, $2$, and $4$, because person $1$’s $1$-st generation descendants are people $2$ and $4$.

The $2$-nd insurance covers people $1$, $2$, $3$, and $4$, because person $1$’s $1$-st generation descendants are people $2$ and $4$, and person $1$’s $2$-nd generation descendant is person $3$.

The $3$-rd insurance covers person $4$, because person $4$ has no $1$-st, $2$-nd, or $3$-rd descendants.
Therefore, four people, people $1$, $2$, $3$, and $4$, are covered by at least one insurance.

Sample Input 2

10 10
1 1 3 1 2 3 3 5 7
2 1
5 1
4 3
6 3
2 1
7 3
9 2
1 2
6 2
8 1

Sample Output 2

10

---

2.Solution

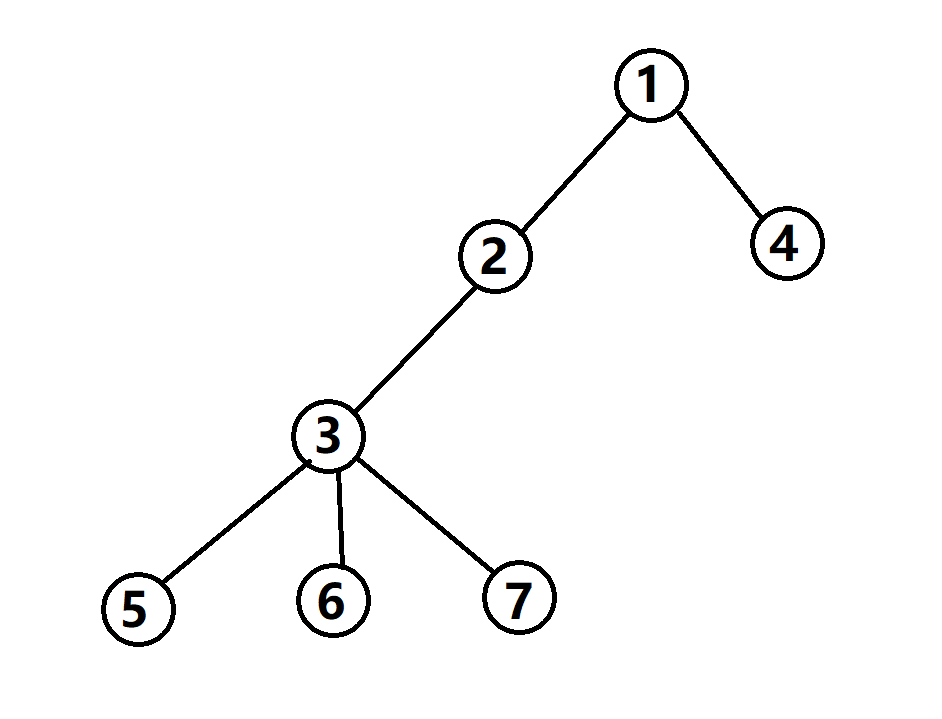
这是样例中所对应的树。

这道题可以运用动态规划。
设 $f_i$ 表示 $i$ 号节点的保险还能延续到多少代。

那么转移就非常简单了：
$f_i=\max (f_i,f_{p_i}-1)$ （注：$p_i$ 即题目中所说的含义）。

之后，就进行对每一个点判断：
如果 $f_i\ge 0$，那么$res++$。

最后的答案就是 $res$。（不太明白的话，可以看看代码~~~）

---

3.Code

#include <iostream>
#include <cstring>

using namespace std;

const int N = 3e5 + 10;

int n, m;
int f[N], p[N];

int main()
{
	cin >> n >> m;
	
	p[1] = 1;
	for (int i = 2; i <= n; i ++)
		cin >> p[i];
	
	memset(f, -1, sizeof f);
		
	while (m --)
	{
		int x, y;
		
		cin >> x >> y;
		
		f[x] = max(f[x], y); //进行最初的赋值，表示x节点可以延续y代
	}
	
	for (int i = 1; i <= n; i ++)
		f[i] = max(f[i], f[p[i]] - 1);
		
	int res = 0;
	for (int i = 1; i <= n; i ++)
		if (f[i] >= 0)
			res ++;
			
	cout << res << endl;
}

4.Time Complexity: $O(N)$

---

F - Box in Box

1. Description

Problem Statement

There are $N$ boxes. The $i$-th box has a shape of a rectangular cuboid whose height, width, and depth are $h_i,w_i$, and $d_i$, respectively.
Determine if there are two boxes such that one’s height, width, and depth are strictly greater than those of the other after rotating them if necessary.

Constraints

$2\le N\le 2\times 10^5$
$1\le h_i,w_i,d_i\le 10^9$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$h_1$ $w_1$ $d_1$
$⋮$
$h_N$ $w_N$ $d_N$

Output

Print Yes if there are two boxes such that one’s height, width, and depth are strictly greater than those of the other after rotating them if necessary; print No otherwise.

Sample Input 1

3
19 8 22
10 24 12
15 25 11

Sample Output 1

Yes

If you rotate the $2$-nd box to swap its height and depth, the $3$-rd box will have greater height, depth, and width.

Sample Input 2

3
19 8 22
10 25 12
15 24 11

Sample Output 2

No

Sample Input 3

2
1 1 2
1 2 2

Sample Output 3

No

---

2. Solution

都放在视频里拉~~~，不懂得话可以再来问我。

ABC 309 F题

线段树没有学的同学可以点这里！

---

3. Code

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;

int n;
struct Node1
{
	int h, w, d;
	void change() //保证h, w, d升序
	{
		if (h > w) swap(h, w);
		if (w > d) swap(w, d);
		if (h > w) swap(h, w);
	}
	bool operator< (const Node1 &t)const //重载小于号
	{
		if (t.h == h)
			return w > t.w;
		return h < t.h;
	}
}cube[N];
vector<int> discrete;
struct Node2
{
	int l, r;
	int mn;
}seg[8 * N]; //*8的原因是我们后面插入的时候为了离散化的方便，将Wi - 1也做成了节点

int find(int x) //离散化
{
	return lower_bound(discrete.begin(), discrete.end(), x) - discrete.begin() + 1;
}

void pushup(int u)
{
	seg[u].mn = min(seg[u << 1].mn, seg[u << 1 | 1].mn);
}

void build(int u, int l, int r) //建树
{
	if (l == r)
		seg[u] = {l, l, 0x3f3f3f3f};
	else
	{
		seg[u] = {l, r};
		int mid = l + r >> 1;
		build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
}

void modify(int u, int x, int d) //单点修改
{
	if (seg[u].l == x && seg[u].r == x)
		seg[u].mn = min(seg[u].mn, d);
	else
	{
		int mid = seg[u].l + seg[u].r >> 1;
		if (x <= mid) modify(u << 1, x, d);
		else modify(u << 1 | 1, x, d);
		pushup(u);
	}
}

int query(int u, int l, int r) //区间查询
{
	if (seg[u].l >= l && seg[u].r <= r)
		return seg[u].mn;
		
	int mid = seg[u].l + seg[u].r >> 1, res = 0x3f3f3f3f;
	if (l <= mid) res = query(u << 1, l, r);
	if (r > mid) res = min(res, query(u << 1 | 1, l, r));
	
	return res;	
}

int main()
{
	cin >> n;
	
	for (int i = 1; i <= n; i ++)
		cin >> cube[i].h >> cube[i].w >> cube[i].d, cube[i].change();
		
	sort(cube + 1, cube + 1 + n);
	
	for (int i = 1; i <= n; i ++) discrete.push_back(cube[i].w), discrete.push_back(cube[i].w - 1);
	sort(discrete.begin(), discrete.end());
	discrete.erase(unique(discrete.begin(), discrete.end()), discrete.end());
	
	build(1, 0, discrete.size());
	
	for (int i = 1; i <= n; i ++)
	{
		int ans = query(1, 0, find(cube[i].w - 1));
		
		if (ans < cube[i].d)
		{
			cout << "Yes" << endl;
			return 0;
		}
		
		modify(1, find(cube[i].w), cube[i].d);
	}
	
	cout << "No" << endl;
}

东望苍苍，西望茫茫，叶落花凋泪满裳