MATLAB之机械原理之解析法之直角坐标法之曲柄摇杆机构和双曲柄运动仿真设计

闲扯：

        最近又变得有时间了。回忆起了去年做的这个小东西，还有很多可以改进的地方，这几天就认真研究了一下，有所感悟，也确实改进升级了一些，完整代码在最下方。（后续好像可以初步做出一个小的gui来实现你给定杆长，就可以生成运动动画的效果，这是后话，最近有时间也会找机会做出来发布）

回顾：

        本文紧接上一篇文章：MATLAB之机械原理之解析法之直角坐标法之曲柄摇杆机构运动仿真设计_matlab怎么表示两杆间夹角固定-CSDN博客

是对上文出现的一些错误进行纠正和一些改进。

如果您对此有兴趣，可以先看看上一篇文章后再阅读这篇文章，可能会更好理解，感谢。

发现错误：

        首先上文说到：

        上述代码通过设定a，b两个未知数，来记录一个位置中的C的位置信息，使用solve来进行求解，后将a，b的信息依次带入C的位移矩阵之中。需要注意的是，也是困扰了我很久的是，联立方程进行求解时，得到a，b会有多解的情况，数学上理解是因为有平方存在，求解时会有正和负两种情况，在机械四杆机构中理解，则是会出现BC杆位于AD下方的情况。

        这个其实是没问题的，但是我误以为得到的解就是一组一组排好队了的，只要选择第一行，就是第一组解，选第二行就是第二组解，这似乎在曲柄摇杆机构中是使用的，但是放到双曲柄机构中就会出现动画跳跃不连续的情况了。

        实际上，利用matlab中的solve函数求解方程，得到多组解的情况，解的信息贮存在矩阵中是按一定规律排序的（似乎是升序，但不满足我们所要求的分组），也就是说上文贮存c点横坐标信息的A矩阵，和组成c点纵坐标信息的B矩阵（都是2×126的大小），除了A,B矩阵相同位置的解信息是对应的，例如A矩阵第2行第三列的横坐标信息对应着B矩阵第2行第三列的纵坐标信息。

其他什么都说明不了，可能A矩阵第一行的前100列都是第一组解的信息，但是第一行101列到125列都是第二组解的信息了，而第一行的126列又是第一组信息了，所以要先对贮存c的坐标信息的A、B矩阵进行预处理，让其变成第一行是一组解，第二行是另一种解，真正实现精确分类。

纠正措施：

        为了纠正这个错误，我苦思冥想了2天，试了好几种方法，就在今天下午终于找到了最最合适的方法（不辛苦命苦）。

        也分享一下我最开始的一些思路，如果大家对我的这个问题有兴趣，可以帮大家开拓思路，

如果对错误不成熟的思路没兴趣，也可以直接看思路三，我的最终处理方法:

思路1：

        我最开始是想，既然运动动画要连续，其实每个精确点之间的距离其实不大，例如每次运动我们设置转动pi/50，其实也就是3.6°，假设边长是130，其实每次转动的幅度很小了，所以如果是同一组坐标，变化量应该不大，如果出现了突变，一下加了很多，或者少了很多，那不就是说明数据不是同一组，就编写个if函数检测，用diff函数计算这一列的值减去前一列的值再取绝对值，如果差值大过阈值，就把这列的第一行第二行换位，如果不超过阈值就说明是同一组的，不换位保持不变。

        我也初步写出了程序，也有一点效果，但是在后续测试中发现几个问题，首先阈值不好确定，不方便后续如果要模块化做一个自动生成器。还有就是，有时候虽然是不同组数据，但其实数值很接近。例如某一列的第一行是180.96，第二行是179.69，就差一点点，根本检测不出来，然后一次检测错误，后续检测更错了，只得先放弃这个思路。（不辛苦命苦+1）

思路2：

        我后面又想到，在机构运动过程中（默认曲柄初始角度60°，曲柄逆时针转动），c点的横坐标是不是先减小，再增大，再减小。是不是可以利用单调性来求解呢，同样利用diff函数，计算矩阵前后素质之间的差，大于0的话就说明单增，小于0就单减。

        但是，先减后增再减的规律是我默认曲柄初始角度60°的情况下得出来的，而且曲柄摇杆机构也不太满足这个情况，无奈再次放弃这个思路。（不辛苦命苦+2）

思路3：

        开始到正题了，主要是用到了机械原理中的错位不连续原理。刚刚开始学这个原理时候也只是用来画图时候检验机构有没有画错，但就在刚刚突然想起来这个原理，在这一样适用。

        何为错位不连续原理呢，太官方的话我就不解释了，可以查阅机械原理这本书或者网上查询一下。我这里用口语简单描述一下其判断方法。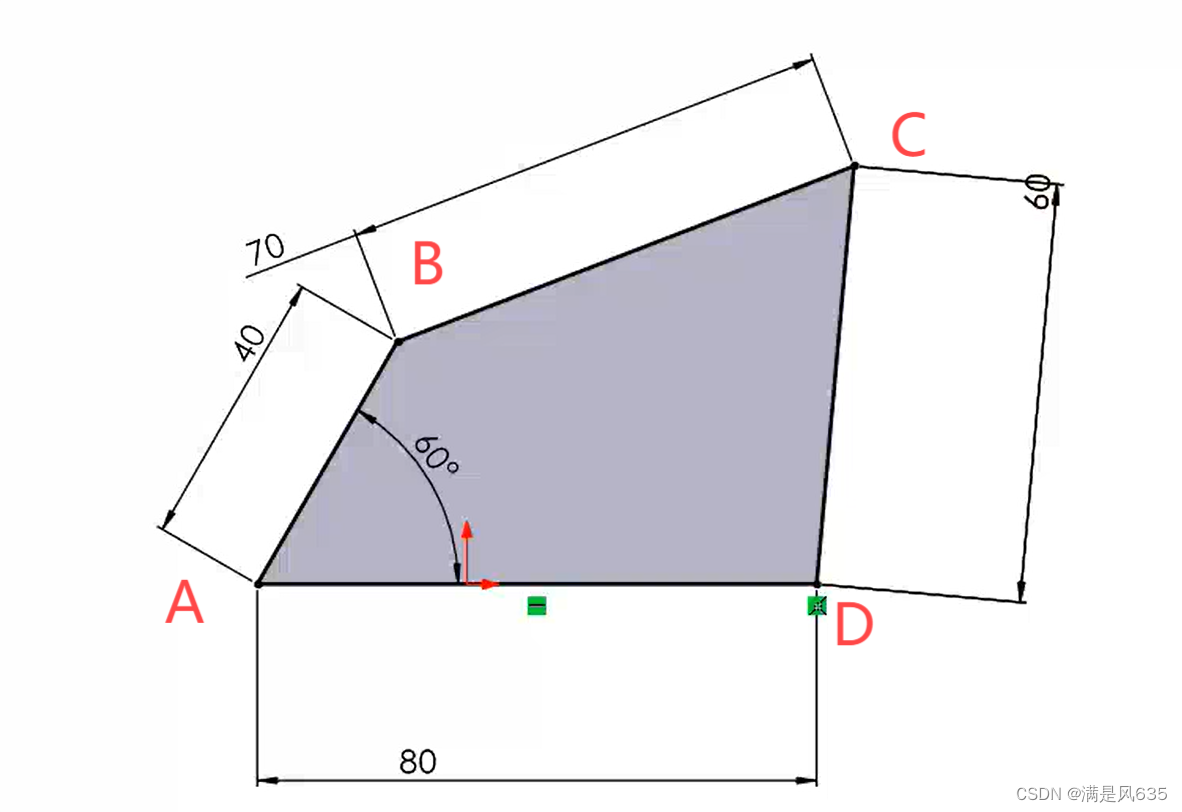

        仔细观察上图，以A点为坐标原点建系，则D的坐标(80,0),而AB杆作为曲柄逆时针运动为原动件，在这个过程中，你假设有一条线，依次穿过B点，C点，D点，无论对应运动到哪个位置，这条线都是顺时针方向（大致效果如下）。

        

        换言之，就是在运动过程中，B点始终在杆CD的一侧（上图对应着始终在杆cd左侧的情况，视角沿着矢量dc看），要么一直在左边，要么一直在右边。结合下列视频观察可能会比较明了。

机构运动1

        仔细观察上方视频的机构运动，重点留心B点相对杆cd的位置，不难发现，在整个运动过程中，B点始终在杆cd的左侧。

机构运动2

        仔细观察上方视频的机构运动，重点留心B点相对杆cd的位置，不难发现，在整个运动过程中，B点始终在杆cd的右侧。

        上边两个视频也就是有两组解对应的运动情况。

修改程序：

        有了这个思路，便开始着手改进程序，最初版本的程序一样可以在上一篇文章中找到，本次的代码其实和其大体一致，核心原理还是机械原理的直角坐标法。但是之前的代码对得到的数据没有处理直接带入使用，容易出现错误情况，本次代码改进好了这一问题。

        具体改进的方法是用上了矢量叉积的知识点，如果感兴趣可以听我给你分析一下，（不感兴趣也可以直接复制下面代码运行就好了）。

        如果有一条线（杆cd），和一个点（b点），只要确保b点一直在杆cd的一侧，在同一侧就是同一组解。而b点始终在杆cd一侧，构建矢量bd，和矢量cd，用矢量bd叉积矢量cd则始终为正或者始终为负（为正可以则b点一直在杆cd右侧，为负则b点一直在杆cd左侧）.

        那我们可以构建两个矢量，一个是vq1，矢量bd；一个是vq2，矢量cd；matlab中矢量叉积函数是cross（），这个函数是对三维矢量进行矢量叉积运算的，所以我们也把vq1，vq2后面加一个0，方便运算。具体操作如下（此处代码只是为了介绍原理，想运行程序不用理会这处代码，直接复制后方完整代码就好）：

for q=1:1:num1
    vq1=[Xb(q)-Xd,Yb(q)-Yd,0]; %矢量bd，后面填个零方便计算
    vq2=[A(1,q)-Xd,B(1,q)-Yd,0]; %矢量cd，后面填个零方便计算
    result=cross(vq1,vq2); %cross叉乘函数，得到一个1×3的矩阵，
    
    if result(1,3)>0 %如果叉乘大于0，也就是说是b点在cd右侧的这组解
        %就把这组解放到第二行去，这样第二行都是b点在cd右侧的这组解，第一行就都是另一种解
        A([1, 2],q)=A([2,1],q);
        B([1, 2],q)=B([2,1],q);
    end
    %将处理好的A、B矩阵信息带入进c点坐标中，A(1,q)的话就是选第一行的那组解，A(2,q)的话就是选第二行的那组解
    Xc(q)=real(A(1,q));
    Yc(q)=real(B(1,q));
end

        矢量叉积得到的结果为一个1×3的矩阵result，重点就看第三个数据，如果这个数据大于0，则说明b点在杆cd右侧，if函数满足条件，就把这个解统一放到第二行去，循环遍历后，就可以将所有b点在杆cd右侧的解都放到第二行去，第一行就都是b点在杆cd左侧的那组解。实现了对解按行分类的目的了。     

        确实是新手，上一篇文章的代码是直接复制在内容上了，这次学乖了（不辛苦命苦+3），详细代码都在下面并配了较为详细的注释，复制全文进matlab中运行就可以了，如果想修改铰链四杆的参数，需要提前规划好铰链四杆机构各个杆长，然后套进程序中就行。

        备注：目前程序只适用曲柄摇杆机构和双曲柄机构，且杆ab为原动件。

        

% 直角坐标法

format long %设置数据格式，高精度
syms a b ; %定义两个变量，a，b

Wa=pi/50; %设置曲柄转速，弧度制
num1=ceil(2*pi/Wa); %根据曲柄转速，则计算转一周有多少精确点

% 设置杆长和a、d点坐标信息
Xa=0;
Ya=0; 
Xd=60.5;
Yd=0;
Lab=80.896;
Lbc=230.5664;
Lcd=221.8;

% 提前为b、c、以及变量A、B、M定义好矩阵大小，都是零矩阵
Xb=zeros(1,num1); 
Yb=zeros(1,num1);
Xc=zeros(1,num1);
Yc=zeros(1,num1);
A=zeros(2,num1);
B=zeros(2,num1);
M=zeros(1,num1);

theatA=pi/3; %设置初始曲柄与x轴角度
f=1:1:num1; %定义f为递增矩阵，增量为1

% M是用来贮存各个精确点角度信息的
M(f)=theatA+Wa*(f-1);

% 计算b点在各个精确点的坐标信息，通过for循环，将各个信息带入进提前准备好的零矩阵中
for i=1:1:num1

    Xb(i)=Xa+Lab*cos(M(i));
    Yb(i)=Ya+Lab*sin(M(i)); 

end

% 通过bc杆已知和cd杆已知还有d坐标已知，列方程求c的坐标信息
%A矩阵贮存c点的横坐标信息，B矩阵贮存c点的纵坐标信息，
%这里通过for循环，是计算每个精确点的c的坐标信息，并将其带入提前准备好的A、B两个零矩阵中
for q=1:1:num1
    eq1=(a-Xd).^2+(b-Yd).^2-Lcd.^2==0; %方程组1，利用dc杆已知列的方程
    eq2=(a-Xb(q)).^2+(b-Yb(q)).^2-Lbc.^2==0; %方程组2，利用bc杆已知列的方程
    [A(:,q),B(:,q)]=solve([eq1,eq2],[a,b]); %求解方程组，并将数据带入A、B矩阵中

end

%到这为止，以及得到了b点的坐标信息，还有c点的坐标信息，（a，d坐标信息也已知）
% 但值得注意的是，上述循环中求解c的坐标会出现多解的情况
% 在数学上解释是因为这是二元二次方程求解，会有多解
% 在机械四杆机构中解释是因为是有两个可行域的（也就是给你这四个杆，是可以有两种装法，也就有两种运动情况）
% 所以还需对A、B这两个矩阵进行处理，最后得到合适的坐标信息，确定出c点坐标

%A、B矩阵都是2×num1大小的矩阵，我最开始以为，A、B的第一行数据就是一组解，第二行数据是第二组解
%这在曲柄摇杆机构中确实适用好像，但在双曲柄机构中就会有问题，运动动画会有跳跃现象，不连续
%利用机构运动的错位不连续原理，可以对解进行分类，分成正确的两组
%错位不连续（机械原理中的知识点），说人话就是，四杆机构在一个可行域内运动时候，b点一直只会在cd杆的一侧（要么左边，要么右边）
%左边是一组解，右边的情况也是一组解，如果b点在cd杆左侧，则矢量bd叉乘矢量cd就小于0，反之大于0的话，b点就在cd杆右侧
for q=1:1:num1
    vq1=[Xb(q)-Xd,Yb(q)-Yd,0]; %矢量bd，后面填个零方便计算
    vq2=[A(1,q)-Xd,B(1,q)-Yd,0]; %矢量cd，后面填个零方便计算
    result=cross(vq1,vq2); %cross叉乘函数，得到一个1×3的矩阵，
    
    if result(1,3)>0 %如果叉乘大于0，也就是说是b点在cd右侧的这组解
        %就把这组解放到第二行去，这样第二行都是b点在cd右侧的这组解，第一行就都是另一种解
        A([1, 2],q)=A([2,1],q);
        B([1, 2],q)=B([2,1],q);
    end
    %将处理好的A、B矩阵信息带入进c点坐标中，A(1,q)的话就是选第一行的那组解，A(2,q)的话就是选第二行的那组解
    Xc(q)=real(A(1,q));
    Yc(q)=real(B(1,q));
end

% 正常绘图
v=moviein(100);

for w=1:1:num1
    clf;   
    hold on
    plot(Xa,Ya,'*r',Xb(w),Yb(w),'*g')
    line([Xa,Xb(w)],[Ya ,Yb(w)]);
    plot(Xb(w),Yb(w),'*',Xc(w),Yc(w),'*')
    line([Xb(w),Xc(w)],[Yb(w),Yc(w)]);
    plot(Xd,Yd,'*r',Xc(w),Yc(w),'*g')
    line([Xd,Xc(w)],[Yd ,Yc(w)]);
    
    axis([-(ceil(Xd+Lcd)+10) ceil(Xd+Lcd)+10 -(ceil(Xd+Lcd)+10) ceil(Xd+Lcd)+10 ])
    v(w)=getframe;
end
 grid
  movie(v)
 hold off

        唠叨几句：

        刚刚结束考研事宜，有些清闲，想起来这个小东西，这几天都在思考改进让其更加高效准确。这次改进确实让我收获很多，虽然看似只是多了一步对数据进行处理分组后再带入画图，但就是这一步也有很多知识点，错位不连续，矩阵运算，矢量叉积等等，也困扰了我两天，所幸最后有了一个较为满意的效果，没让我大败而归。

        最后再总结一下：

        其实这次改进就是修复了上一篇文章中的小bug，更为合理了，更有理论支撑了，其主要就是结合了机械原理的错位不连续原理和矢量叉积原理。本文是对上一篇文章的补充改进，如果感兴趣，希望能够先阅读上一篇文章后，（上方有链接）再来思考这篇文章，我觉得还是很有意思的，也可以提前在b站上温习一下矢量叉积和错位不连续的知识点方便理解。

        后续应该会继续完成之前的小目标，通过matlab的gui设计成一个曲柄摇杆生成器，这次改进其实也已经向这个目标迈出了坚实的一步。若有成果，后续会继续发布。

        本人学习matlab时间不长，也并非专业计算机编程专业，纯属兴趣爱好，若有人对此感兴趣，有任何看法或建议，都很欢迎在评论区留言讨论。你能看到这，我已经万分感谢。