学习《图解密码技术》记录学习第五章中RSA算法的加密与解密

最新推荐文章于 2024-07-19 14:50:02 发布

御风楼@主人

最新推荐文章于 2024-07-19 14:50:02 发布

阅读量604

点赞数 13

文章标签：密码学

本文链接：https://blog.csdn.net/weixin_67944207/article/details/138151985

版权

RSA加密公式：

在RSA中,明文、密钥和密文都是数字。RSA的加密过程可以用下列公式来表达,这个公式很重要，因此我们把它框起来。

密文= 明文^E mod N (RSA加密公式)

RSA 的密文是对代表明文的数字的E次方求 mod N的结果，这个余数就是密文。

加密公式中出现的两个数——E 和 N，到底都是什么数呢？RSA 的加密是求明文的E 次方 mod N，因此只要知道 E 和 N 这两个数，任何人都可以完成加密的运算。所以说，E 和N 是 RSA 加密的密钥，也就是说，E 和 N 的组合就是公钥。

有一个很容易引起误解的地方需要大家注意——E和N这两个数并不是密钥对（公钥和私钥的密钥对)。E 和 N 两个数才组成了一个公钥，因此我们一般会写成“公钥是(E,N)”或者“公钥是{E,N}”这样的形式，将E和N用括号括起来。

RSA解密公式：

明文=密文^D mod N (RSA解密公式)

对表示密文的数字的 D 次方求 mod N 就可以得到明文。

这里所使用的数字 N 和加密时使用的数字 N 是相同的。

数 D 和数 N 组合起来就是 RSA 的解密密钥，因此D 和 N 的组合就是私钥。只有知道 D 和 N两个数的人才能够完成解密的运算。

大家应该已经注意到，在 RSA 中，加密和解密的形式是相同的。加密是求“E 次方的 modN”，而解密则是求“D 次方的 mod N”，这真是太美妙了。

当然，D也并不是随便什么数都可以的，作为解密密钥的 D，和数字 E 有着相当紧密的联系。否则,用E加密的结果可以用D来解密这样的机制是无法实现的。

加密与解密公式如下图：

生成密钥对

刚刚已经讲过，RSA 的加密是求“E 次方的 mod N”，解密是求“D 次方的 modN”，那么这里需要用到的三个数——E、D 和 N 到底应该如何生成呢？

由于E 和 N 是公钥，D 和 N 是私钥，因此求E、D 和 N这三个数就是生成密钥对。RSA 密钥对的生成步骤如下。

(1)求 N

(2)求L(L是仅在生成密钥对的过程中使用的数)

(3)求 E

(4)求D

下面我们逐一来进行讲解。

(1)求 N

1.首先准备两个很大的质数（关键字：很大质数，太小容易被破解质数：质数是指只能被1和自身整除的正整数，即除了1和它本身以外没有其他正整数能整除它，类如：2、3、5、7、11等都是质数，因为它们只能被1和自身整除。相反，像4、6、8、9等数都不是质数，因为它们可以被除了1和自身以外的其他数整除。）

2.我们将这两个很大的质数称为p和q

3.准备好两个很大的质数之后，我们将这两个数相乘，其结果就是数 N。也就是说，数 N可以用下列公式来表达。

N=px q (p、q为质数)

举例（举例数字我就弄小一点）

𝑝=7 和 q=11

N=px q

=77

(2)求L

下面我们来求数L。

L这个数在RSA的加密和解密过程中都不出现,它只出现在生成密钥对的过程中。

L是p-1和q-1的最小公倍数(最小公倍数，lcm)如果用lcm(X,Y)来表示“X和Y的最小公倍数”，则L可以写成下列形式。

L= Icm(p -1, q-1) (L是p-1和q-1的最小公倍数)

求最小公倍数公式：LCM(a,b)×GCD(a,b)=a×b

先将lcm（p-1，q-1）中的p-1套入上述公式即等于：a

q-1套入上述公式即等于：b

GCD（是求最大公约数，根据欧几里德算法来计算两个整数的最大公约数）：

欧几里德算法:GCD(a,b)=GCD(b,amodb)

GCD(a,b) 表示两个正整数 𝑎a 和 𝑏b 的最大公约数，mod 是求模运算，表示取 𝑎a 除以 𝑏b 的余数。欧几里德算法的递归特性：每次迭代都将原来的两个数转化为较小的数和余数。最终，当余数为0时，较小的数即为两个整数的最大公约数。

假设我们要计算整数48和18的最大公约数。

48➗18商=2，余数12。
18➗12商=1，余数6。
12➗6商=2，余数0。

因为最后的余数是0，所以最大公约数为前一个除数，即6。

所以，48和18的最大公约数是6。

例如，对于数56和42，用辗转相除法进行计算：

56 ÷ 42 商= 1，余数14
42 ÷ 14 商= 3，余数0

因为最后的余数为0，所以42和56的最大公约数为14。

好的，让我们用小一点的数来举例说明。

𝑝=7 和 q=11。

首先，我们计算 𝐿=LCM(𝑝−1,𝑞−1)

=LCM(7-1,11-1)

=LCM(6,10)

将LCM(6,10)套入求最小公倍数公式：LCM(a,b)×GCD(a,b)=a×b

LCM(6,10)×GCD（6，10）=6×10

LCM(6,10)×GCD（6，10）=60

LCM(6,10)=60➗GCD（6，10）

欧几里德算法:GCD(a,b)=GCD(b,amodb)

即： LCM(6,10)=60➗GCD（10，6mod b）

GCD（10，6mod b）=10➗6商=1 余数4

6➗4商=1 余数 2

4➗2商=2 余数0

LCM(6,10)=60➗2

=30

即：L=30

(3)求E

下面我们来求数 E。

E 是一个比 1 大、比L 小的数。此外，E 和L 的最大公约数必须为1。如果用ged(X, Y)来表示X和Y的最大公约数,则E和L之间存在下列关系。

1<E<L

GCD(E, L) = 1 E和L的最大公约数为1（E和L互质)

要找出满足 GCD(E，L) = 1 的数，还是要使用伪随机数生成器。通过伪随机数生成器在 1 < E<L 的范围内生成E的候选数,然后再判断其是否满足 GCD(E, L) = 1 这个条件。求最大公约数可以使用欧几里得的辗转相除法。

L=30,那么满足条件的有：4、7、8、9、11、12、13、14、16、17、18、19、20、21、22、23、24、25、26、27、28、29

简单来说,之所以要加上E和L的最大公约数为1这个条件,是为了保证一定存在解密时需要使用的数 D。

现在我们已经求出了E和N，也就是说我们已经生成了密钥对中的公钥。

(4)求D

下面我们来求数 D。

数D是由数E计算得到的。D、E和L之间必须具备下列关系。

1<D<L

E x D mod L = 1

E=4、7、8、9、11、12、13、14、16、17、18、19、20、21、22、23、24、25、26、27、28、29 假设我们取得的是其中的质数7

L=30

则 7×Dmod 30 = 1

因为数小我们就逐步尝试：

当 (D = 1 ) 时， (7 × 1 mod 30 = 7 mod 30 = 7 )，不满足条件。
2. 当 (D = 2 ) 时， (7 × 2 mod 30 = 14 mod 30 = 14 )，不满足条件。
3. 当 (D = 3 ) 时， (7 × 3 mod 30 = 21 mod 30 = 21 )，不满足条件。
4. 当 (D = 4 ) 时， (7 × 4 mod 30 = 28 mod 30 = 28 )，不满足条件。
5. 当 (D = 5 ) 时， (7 × 5 mod 30 = 35 mod 30 = 5 )，不满足条件。
6. 当 (D = 6 ) 时， (7 × 6 mod 30 = 42 mod 30 = 12 )，不满足条件。
7. 当 (D = 7 ) 时， (7 × 7 mod 30 = 49 mod 30 = 19 )，不满足条件。
8. 当 (D = 8 ) 时， (7 × 8 mod 30 = 56 mod 30 = 26 )，不满足条件。
9. 当 (D = 9 ) 时， (7 × 9 mod 30 = 63 mod 30 = 3 )，不满足条件。
10. 当 (D = 10 ) 时， (7 × 10 mod 30 = 70 mod 30 = 10 )，不满足条件。
11. 当 (D = 11 ) 时， (7 × 11 mod 30 = 77 mod 30 = 17 )，不满足条件。
12. 当 (D = 12 ) 时， (7 × 12 mod 30 = 84 mod 30 = 24 )，不满足条件。
13. 当 (D = 13 ) 时， (7 × 13 mod 30 = 91 mod 30 = 1 )，满足条件。
D=13

只要数 D 满足上述条件,则通过E和N进行加密的密文,就可以通过D 和 N 进行解密。

E × D mod L=1 这样的公式在上一节的时钟运算中也出现过（5.5.4 节)。要保证存在满足条件的D,就需要保证E和L的最大公约数为1，这也正是(3)中对E所要求的条件。

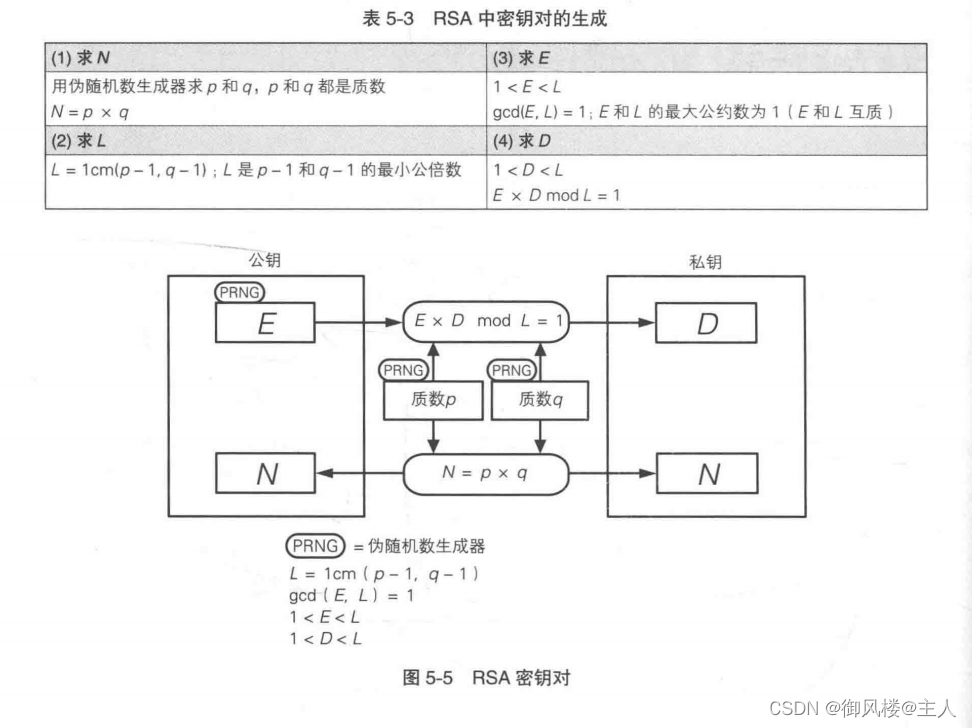
简单来说，E x D mod L=1 保证了对密文进行解密时能够得到原来的明文。现在我们已经求出了 D 和 N，也就是说我们也生成了密钥对中的私钥。上面的内容中出现了很多符号和公式，我们先来整理一下（表5-3、图 5-5）。