dp处理旅行商问题

目录

1.问题陈述

2.基本思想

3.算法描述

4.算法程序代码及其结果

5.算法分析

6.算法运行过程

7.解决题目的源代码程序

---

1.问题陈述

某售货员要到若干个城市去推荐商品，已知各城市之间的路程(或旅费)。他要选定一条从驻地出发，经过其它每个城市有且仅有一次，最后回到驻地的路线，使总路程(或旅费)最小。

用下面图形来举例，有四个地区：

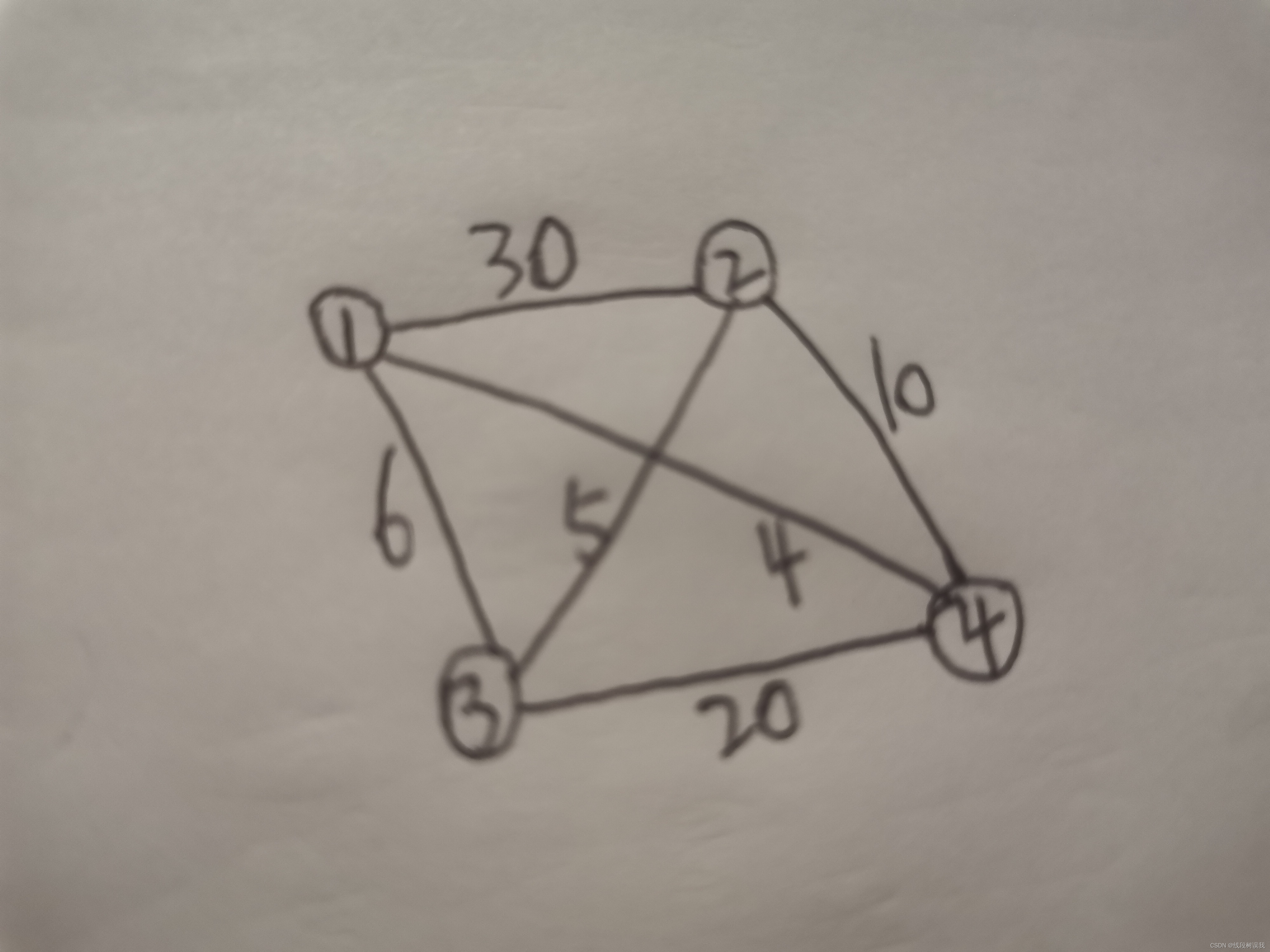
2.基本思想

• 解决方法：首先尝试暴力解法，枚举点的全排列，假设有n个点的话，那么共有n!个全排列，一个排列就是一条路径，那么时间复杂度就达到了O(n!)，这里我们使用状态压缩dp来处理这个问题，那么时间复杂度将降低到O()
• 图的保存形式：设G=(V,E)是一个有n个顶点的无向带权图，V表示点，E表示边，在程序中采       用邻接矩阵来保存这类图并进行dp处理
• 状态压缩DP的处理：将问题的状态用二进制位来表示，每个二进制位代表某个状态的存在或    缺失。通过位运算和状态压缩技巧，可以将状态压缩为一个整数，用该整数来表示问题的状态。

3.算法描述

• 状态压缩是dp的一个小技巧，一般应用于集合问题里面。主要是把对dp状态的处理转换为二进制的位操作，让代码变的简洁和提高算法效率；
• 首先定义dp的状态，用dp[S][j]表示从起点出发经过集合S里面的所有点最终到达终点j时的最短路径，然后根据dp思想，让集合S从小集合递推到大集合，逐步扩展到整个图，最终得到的下面代码的最终结果就是答案，此时的S表示包含图上所有点的集合,k∈(1,n)；    

min(dp[S][k]+dis[k][1])

• 如何求dp[S][j]?可以从S-j集合递推到S集合，假设有一点k它在S-j集合里面，那么dp[S][j]状态就可以由dp[S-j][k]状态推导出来，状态转移方程如下所示，集合S初始时只包含起点，然后逐步将图中的顶点包含进来，直到最后包含所有点。这个过程用状态转移方程实现；

  dp[S][j]=min(d[S][j],dp[S-j][k]+dis[k][j])

• 如何操作集合S?用一个二进制数表示集合S,这个二进制上的每一位都代表图上的一个点，该位置上值为1表示该点在集合里面，为0表示该点不在集合里面，例如S=1010,其中1的位置分别处在2、4位(因为地图是从1开始编号，所以这里用逻辑序号表示），表示集合中包含这两个点。

4.算法程序代码及其结果

int n;  //点的个数，也就是城市数量
int dis[21][21]； //保存城市之间的信息，邻接矩阵保存
int dp[1<<20][21]; //状态转移数组
int yasuodp(int n,int **dis){	
	memset(dp,0x3f,sizeof(dp));//初始化为最大值	
	dp[1][1]=0;  //dp初始状态，集合S里面只包含点1，起点和终点都是1，值为0	
	for(int s=1;s<(1<<n);s++)//从小集合0001遍历到整个图1111，共2^n次		
	{	
		for(int i=1;i<=n;i++)//枚举点	
		{	
			if((s>>(i-1))&1)//判断点i是否在集合里面
				for(int j=1;j<=n;j++)//枚举到达i的点j
		             if((s^(1<<(i-1)))>>(j-1)&1)//判断点j是否在集合s-i里面						
						        dp[s][i]=min(dp[s][i],dis[j][i]+dp[s^(1<<(i-1))][j]);			
		}		
	}
	int result=dp[(1<<n)-1][1];	
	for(int i=1;i<=n;i++)		
		result=min(result,dp[(1<<n)-1][i]+dis[i][1]）;//遍历求最小值			
			return result;			
}

上面图运行结果如下(文章最后会附上源代码，这个函数只是做个介绍)：

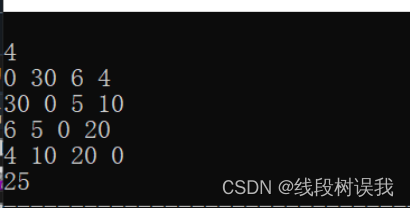
说明：

• s>>(i-1))&1

说明：判断点i是否在S集合里面(集合S里面的序号是从0开始编号的)原理：i因为是表示逻辑序号，所以第i位实际上是表示集合S里面的第(i-1)位，判断点i在不在集合里面，就是判断集合S的第(i-1)位是不是为1，首先使用位运算右移符号‘>>’将集合S中的第(i-1)位移动到第一位[s>>(i-1)]，然后与1相与，如果结果为1就表示集合S里面的第(i-1)位为1，表明点i在集合S里面

• s^(1<<(i-1))

说明：将集合S里面的第(i-1)位赋为0

原理：1<<(i-1)表明将1左移(i-1)位，旨在构造一个二进制数[1...(i-1)个0]，然后与集合S相异或，就可以将集合S里面的第(i-1)位赋为0，得到集合(S-i)

• s^(1<<(i-1))>>(j-1)&1

说明：判断点j是否在S-i集合里面

原理:前两个运算的结合，s^(1<<(i-1))不多解释，就是构造S-i集合，将集合s里面的第(i-1)位赋为0，然后>>(j-1)&1就是判断点j是否在S-i集合里面

5.算法分析

时间复杂度：时间复杂度从O(n!)降低到了O(),由代码可知算法主要由3个for循环构成，第1个for循环从1遍历到-1,共有约次，所以复杂度约为O()，在加上后面两个各n次的for循环，所以总复杂度为O()

可知当n=8时O(n!)的复杂度已经超过了O()的复杂度，并且在n=20时，O(n!)的复杂度已经达到了O()复杂度的上亿倍。

优点：

• 算法效率高：状态压缩DP可以大幅度减少计算时间，尤其在处理指数级别的状态空间时，相对于传统的动态规划算法，它可以显著提高算法的效率。
• 时间复杂度低：通过状态压缩技巧，可以避免重复计算相同的子问题。这可以进一步加速算法的执行速度，大幅减少算法的计算时间。

缺点

•  实现复杂：状态压缩DP相对于传统的动态规划算法来说，实现难度较高。需要处理位运算相关的操作，这可能增加了代码的复杂性和难度。
• 不适用于所有问题：状态压缩DP适用于满足子问题的无后效性和最优子结构性质的问题。

改进方法：

•  动态规划剪枝：使用动态规划剪枝技术来减少不必要的计算，提前终止某些分支的计算，以减少计算量。
• 邻近搜索策略：通过邻近搜索策略指导状态压缩DP的计算过程，优先考虑与当前状态相邻的状态，以有针对性地搜索最优解。

6.算法运行过程

dp的初始状态除了dp[1][1]=0外，其他值都初始化为最大值,又可知集合s是由集合s-i推导出来的，所以如果集合s-i里面不包含起点1的话，那么dp的值是肯定为最大值的。如下所示：

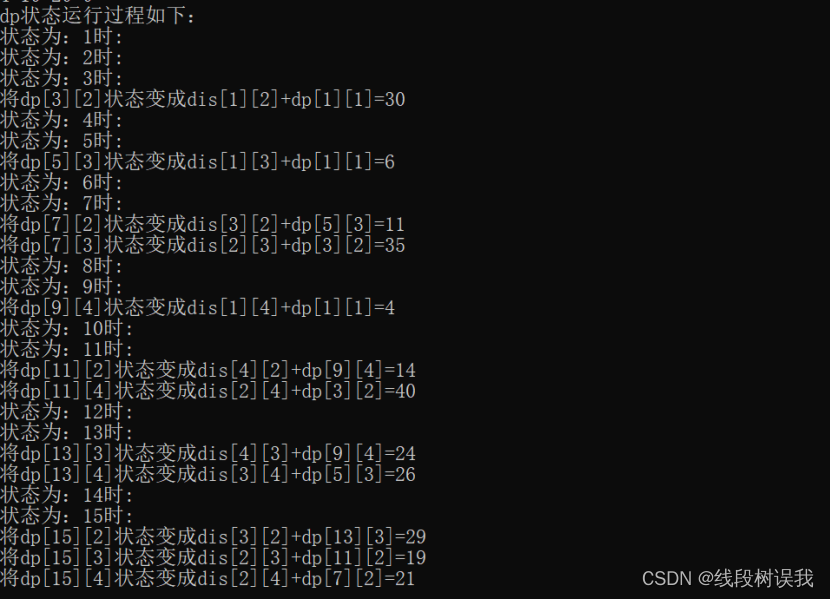
当你的状态处在不包含起点时，是肯定求得最大不会有所改变的，保持原最大值。

最后当求得所有dp最优状态时，根据代码

  int result=dp[(1<<n)-1][1];     
     for(int i=1;i<=n;i++)         
         result=min(result,dp[(1<<n)-1][i]+dis[i][1]； 

  求出最终结果，因为求得的dp[s][i]表示从起点出发经过集合S里面的所有点最终到达终点i时的最短路径,所以最后要加上dis[i][1],表示最终返回起点

7.解决题目的源代码程序

#include <bits/stdc++.h>
using namespace std;
int dis[21][21], dp[1 << 20][21];
int main() {
	int n;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++)
			scanf("%d", &dis[i][j]);
	}
	memset(dp, 0x3f, sizeof(dp));
	dp[1][1] = 0;
	for (int s = 1; s < (1 << n); s++) {
		for (int i = 1; i <= n; i++) {
			if ((s >> (i - 1)) & 1)
				for (int j = 1; j <= n; j++)
					if ((s ^ (1 << (i - 1))) >> (j - 1) & 1)
						dp[s][i] = min(dp[s][i], dis[j][i] + dp[s ^ (1 << (i - 1))][j]);
		}
	}
	int result = dp[(1 << n) - 1][1];
	for (int i = 1; i <= n; i++) {
		result = min(result, dp[(1 << n) - 1][i] + dis[i][1]);
	}
	printf("%d", result);
}