代入定理也就是整体替换,能够进行整体替换的原因是每一个逻辑变元的运算结果非1即0,无论是单个逻辑变元还若干个逻辑变元经过运算之后,都是这个结果,所以可以使用一个逻辑式来代替一个逻辑变元。


以上是带入定理的两个例子。通过代入定理可以将之前学过的两变量公式进而拓展为多变量公式。
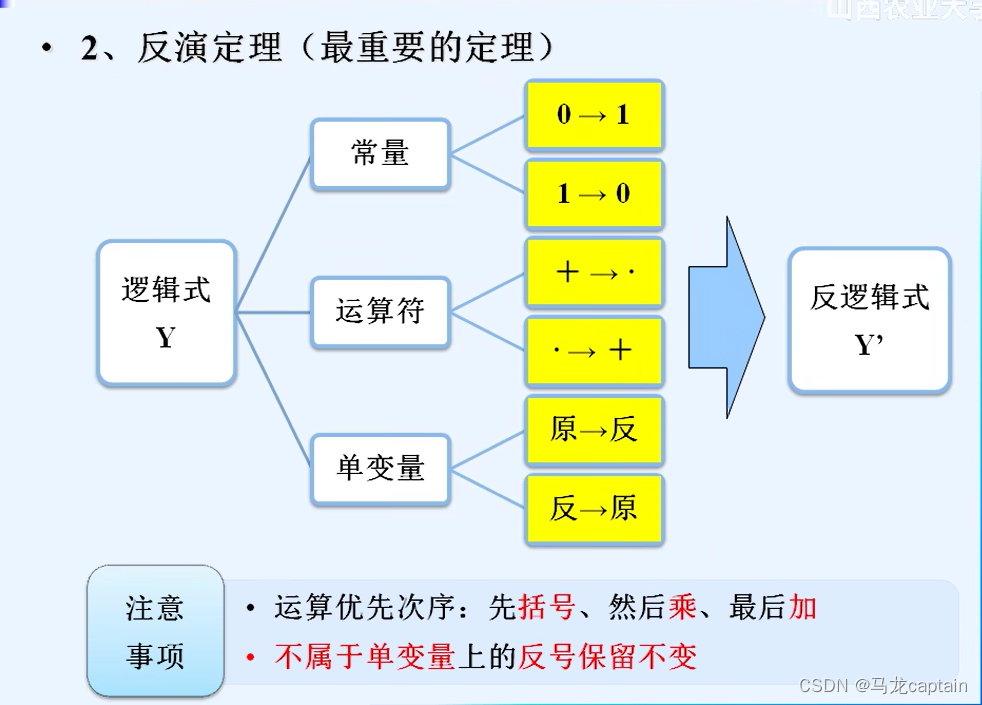
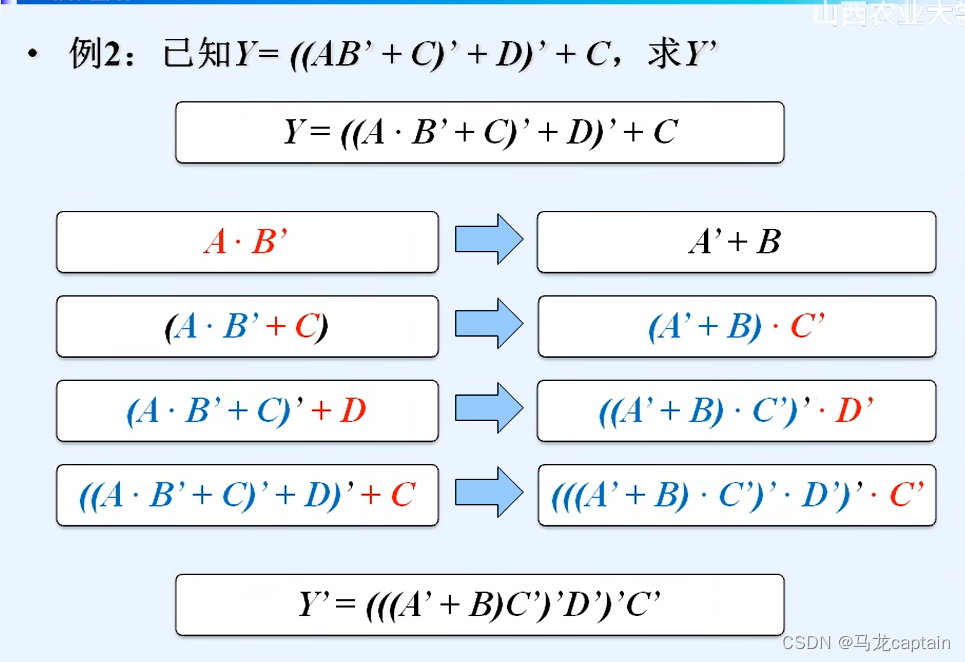
一个逻辑式可以通过反演定理得到它的反逻辑式。


对偶定理:

代入定理也就是整体替换,能够进行整体替换的原因是每一个逻辑变元的运算结果非1即0,无论是单个逻辑变元还若干个逻辑变元经过运算之后,都是这个结果,所以可以使用一个逻辑式来代替一个逻辑变元。


以上是带入定理的两个例子。通过代入定理可以将之前学过的两变量公式进而拓展为多变量公式。

一个逻辑式可以通过反演定理得到它的反逻辑式。



对偶定理:


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


