数据结构
测试题
1.舞会[dance.cpp]
在一个不知名院校与中南大学的联谊舞会上,男士们和女士们同时进入舞厅时,各自排成一队。跳舞开始时, 依次从男生队(m 人,不超过 100)和女生队(w 人,不超过 100)的队列头部各出一人配成舞伴。规定每 个舞曲只能有一对跳舞者。若两队初始人数不相同,则较长的那一队中未配对者等待下一轮舞曲。现要求 写一个程序,模拟上述舞伴配对问题,输出每一首舞曲出场的舞伴的编号。 已经给出了“队列”类的部分代码,这是一个循环队列,你需要完善其中的 push()、pop()、front()、empty()、 full()函数。
【输入样例】 3 4 //第一行为两队的人数 m,w 10 //第二行为舞曲的数目 num(不超过 1000)
【输出样例】 // 共 num 行,每行 2 个整数,分别表示男女舞伴的编号 1 1 2 2 3 3 1 4 2 1 3 2 1 3 2 4
#include<bits/stdc++.h>
using namespace std;
const int MAXSIZE = 10000;
template<class T>
class cQueue
{ int head, tail, maxSize;
T *data;
public:
cQueue();
~cQueue();
void push(const T& x);
T front();
void pop();
bool empty();
bool full();
int size();
void clear();
};
template<class T>
cQueue<T>::cQueue()
{ data = new T[MAXSIZE];
maxSize = MAXSIZE;
head = tail = 0;
}
template<class T>
cQueue<T>::~cQueue()
{ delete data;
}
template<class T>
void cQueue<T>::push(const T& x)
{
data[tail++]=x;
tail=tail%maxSize;
}
template<class T>
T cQueue<T>::front()
{
return data[head];
}
template<class T>
void cQueue<T>::pop()
{
head++;
head=head%maxSize;
}
template<class T>
bool cQueue<T>::empty()
{
return head==tail;
}
template<class T>
bool cQueue<T>::full()
{
return head==(tail+1)%maxSize;
}
template<class T>
int cQueue<T>::size()
{ return (tail - head + maxSize)%maxSize;
}
template<class T>
void cQueue<T>::clear()
{ head = tail = 0;
}
int main()
{ int m, w, num;
cQueue<int> qM, qW;
cin>>m>>w>>num;
for(int i=1; i<=m; i++) qM.push(i);
for(int i=1; i<=w; i++) qW.push(i);
for(int k=1; k<=num; k++)
{ cout<<qM.front()<<" "<<qW.front()<<endl;
qM.push(qM.front()); qM.pop();
qW.push(qW.front()); qW.pop();
}
qM.clear();
for(int i=1; i<=MAXSIZE-1; i++) qM.push(i);
if(qM.full()) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
for(int i=1; i<=10; i++) qM.pop();
for(int i=1; i<5; i++) qM.push(i);
if(qM.full()) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
错误点:判满时,返回的是 return head ==(tail+1)%maxSize;两个等于号
2.栈[stack.cpp]
程序实现了“栈”的功能,输入正整数 n,则将整数 1 至 n 压入栈,然后依次输出栈里的所有数据。 main()函数已经完成,你仅仅需要完善“栈”类的所有函数。 【输入样例】6 【输出样例】 6 5 4 3 2 1 Yes
#include<bits/stdc++.h>
using namespace std;
const int MAXSIZE = 10000;
template<class T>
class cStack
{ int head, maxSize;
T *data;
public:
cStack();
~cStack();
bool push(const T& x);
T top();
void pop();
bool empty();
bool full();
int size();
void clear();
};
template<class T>
cStack<T>::cStack()
{
maxSize=MAXSIZE;
head=-1;
data=new T[maxSize];
}
template<class T>
cStack<T>::~cStack()
{
delete data;
}
template<class T>
bool cStack<T>::full()
{
return head==maxSize-1;//注意这个!!是maxSize-1
}
template<class T>
bool cStack<T>::push(const T& x)
{
if(!full())//要先判断是否满了
{
data[++head]=x;
return true;//因为是bool类型的 所以有个返回值true
}
else
{
return false;
}
}
template<class T>
T cStack<T>::top()//注意 cStack<T>
{
return data[head];
}
template<class T>
void cStack<T>::pop()
{
head--;
}
template<class T>
bool cStack<T>::empty()
{
return head==-1;
}
template<class T>
int cStack<T>::size()//?
{
return head+1;//因为head是从-1开始的
}
template<class T>
void cStack<T>::clear()//注意这个!!
{
head=-1;
}
int main()
{ int n;
cStack<int> st;
cin>>n;
for(int i=1; i<=n; i++) st.push(i);
while(st.size())
{ cout<<st.top()<<endl;
st.pop();
}
st.clear();
for(int i=1; i<=MAXSIZE; i++) st.push(i);
if(st.full()) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
错误点:每个函数名称都是cStack,注意写!构造函数和析构函数前没有函数类型
3.分段逆转链表【rlink.cpp】
给定一个带头结点的单链表和一个整数 K,要求你将链表中的每 K(不大于 100)个结点做一次逆转。 例如给定单链表 1→2→3→4→5→6 和 K=3,你需要将链表改造成 3→2→1→6→5→4;如果 K=4,则应该 得到 4→3→2→1→5→6。第一个输入 n 表示构造一个从 1 到 n 的链表,第二个输入表示逆转的结点数。
#include<bits/stdc++.h>
using namespace std;
struct tNode
{ int data;
tNode *Next;
};
tNode *creatLink(int n);
tNode *revLink(tNode *head, int k);
int N, K;
int main()
{ tNode *head;
cin>>N>>K;
head = creatLink(N);
head = revLink(head,K);
while(head != NULL)
{
cout<<head->data<<" ";
head = head->Next;
}
return 0;
}
tNode *creatLink(int n)
{ tNode *head = new tNode;
head->data = 1;
head->Next = NULL;
tNode *cur = head;
for(int i=2; i<=n; i++)
{
tNode * tmp = new tNode;
tmp->data = i;
tmp->Next = NULL;
cur->Next = tmp;
cur = tmp;
}
return head;
}
tNode *revLink(tNode *head, int k)
{
tNode* tmp1=head;
tNode* tmp2=head;
int len;
int xunhuan;
int i , j;
while (tmp2!=NULL)
{
tmp2=tmp2->Next;
len++;
}
xunhuan=len/k;
for (j=1;j<=xunhuan;j++)
{
for ( i=0;i<k;i++)
{
tmp1->data=j*k-i;
tmp1=tmp1->Next;
}
}
return head;
}
/*
测试样例:
1、 输入:6 3
输出:3 2 1 6 5 4
2、 输入:6 4
输出:4 3 2 1 5 6
3、 输入:7 3
输出:3 2 1 6 5 4 7
4、 输入:7 4
输出:4 3 2 1 5 6 7
5、 输入:8 2
输出:2 1 4 3 6 5 8 7
*/
4.插入排序【insert.cpp】
输入 n(n<=10 7)个 int 范围的整数,采用直接插入排序算法对这些数据从小到大排序。输出每一趟排 序后的数据。
【输入样例】 5 // n 30 30 900 800 800
【输出样例】
30 30 900 800 800
30 30 900 800 800
30 30 800 900 800
30 30 800 800 900
#include<bits/stdc++.h>
using namespace std;
const int MAXSIZE = 10000;
int A[MAXSIZE];
void insert(int a[], int n)
{
int p,i,j;
for(i=1; i<n; i++)
{
int temp=a[i];
p=i;//空位置
for(j=i-1; j>=0; j--) //依次比较
{
if(temp<a[j])
{
a[p]=a[j];
p=j;
}
else
{
break;
}
}
a[p]=temp;
for(int k=0;k<n;k++)
{
cout<<a[k]<<" ";
}
cout<<endl;
}
}
int main()
{
int n;
cin>>n;
for(int i=0; i<n; i++) cin>>A[i];
insert(A, n);
return 0;
}
错误点:注意处理输出的位置
5.第 K 大的数【kBig.cpp】
输入 n(n<=10 7)个数,每个数都是介于 0 到 m(m<=10000)之间的整数,输出数据中第 k(k<=n) 大的数。
【输入样例】 5 1000 3 // n, m, k
30 30 900 800 800
【输出样例】800
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m,k;
cin>>n>>m>>k;
int a[1000];
for(int i=0;i<n;i++)
{
cin>>a[i];
}
sort(a,a+n);
cout<<a[k]<<endl;
return 0;
}
6.二分查找【bSearch.cpp】
利用二分查找算法实现 int sqrt(int x)函数。sqrt(x)计算并返回正整数 x 的平方根。由于返回类型是整数, 结果只保留整数的部分,小数部分将被舍去。 提示: 1)函数应返回最准确的平方根值。例如,224 的平方根是 15 而不是 14。 2)二分查找的下界为 1,初始上界可以设定为 x。在二分查找的每一步中,我们只需要比较中间元素 mid 的平方与 x 的大小关系,并通过比较的结果调整上下界的范围。 输入格式:正整数 x 输出格式:x 的平方根(整数) 【样例输入 1】225 【样例输出 1】15
【样例输入 2】257 【样例输出 2】16
#include<bits/stdc++.h>
using namespace std;
int Sqrt(int x)
{
int L=1,R=x;
while(L<=R)
{
int mid=(L+R)/2;
if(mid*mid<x)
{
L=mid+1;
}
else
{
R=mid-1;
}
}
//返回最准确的平方根值
if(abs(x-L*L)<=abs(x-(L-1)*(L-1)))
{
return L;
}
else
{
return L-1;
}
}
int main()
{ int a;
cin >> a;
cout << Sqrt(a);
return 0;
}
7.最小和之和【minSum.cpp】
在一组数据中,记所有比数字 A 小的数的和为 A 的最小和。例如在 1 3 4 5 中,1 的最小和为 0, 3 的最 小和为 1,4 的最小和为 1+3=4,5 的最小和为 1+3+4=8。要求: 1)将给出的 20 个数据从小到大打印出来,以一个空格分隔,最后一位数字后无空格但需要换行。 2)求给出的 20 个数据中所有数字最小和之和并输出结果。 注意: 1、给出的每组数据中不会出现大小相等的数字; 2、数据都为自然数,且不大于 10000。
【输入样例】20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
【输出样例】 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1140
#include<bits/stdc++.h>
#include<algorithm>
using namespace std;
int main()
{
int a[20];
for(int i=0;i<20;i++)
{
cin>>a[i];
}
sort(a,a+20,less<int>());
for(int k=0;k<20;k++)
{
cout<<a[k]<<" ";
}
cout<<endl;
int res=0;
for(int j=0;j<20;j++)
{
int sum=0;
for(int p=0;p<j;p++)
{
sum=sum+a[p];//注意这里不是p,是a[p]!!!!
}
res=res+sum;
}
cout<<res<<endl;
return 0;
}
8.铁轨【railway.cpp]
每辆火车都从 A 方向驶入车站 C,再从 B 方向驶出车站 C,同时它的车厢可以进行某种形式的重新组 合。组合方式为:最晚驶入车站 C 的车厢停在最前面,可在任意时间将停在最前面的车厢驶出车站 C。假 设从 A 方向驶来的火车有 n 节车厢(n<=1000),分别按顺序编号为 1,2,…,n。假定在进入车站之前每节车 厢之间都是不连着的,并且它们可以自行移动,直接到处在 B 方向的铁轨上。另外假定车站 C 里可以停放 任意多节的车厢。但是一旦当一节车厢进入车站 C,它就不能再回到 A 方向的铁轨上了,并且一旦当它进 入 B 方向的铁轨后,它就不能再回到车站 C。负责车厢调度的工作人员需要知道能否使它以 a1,a2,…, an 的顺序从 B 方向驶出。 请写一个程序,用来判断能否得到指定的车厢顺序。 输入格式: 第一行输入 t(1<=t<=10),表示测试数据的组数。 第一行一个整数 n,表示有 n 节车厢。 接下来一行有 n 个整数,表示对应顺序。 输出格式: 输出仅一行。若可以,则输出“Possible”,否则输出“Impossible”。
【输入样例】 1 5 3 5 4 2 1
【输出样例】Possible
#include <iostream>
#include <stack>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)//对于每一组来说
{
int n;
cin>>n;//每一组中车的数量
int a[n];//将预期的输出序列存放在里面
bool flag=true;
for(int i=0; i<n; i++) //注意循环还是i
{
cin>>a[i];
}
stack<int> s;//代表车站c
int cur=1;//cur代表此时准备的输出的那辆车编号 1 2 3 4 5
for(int i=0; i<n; i) //注意循环还是i
{
while(!s.empty() && a[i]==s.top())//此时栈顶不空且栈顶就等于应该驶出的那个编号,那就驶出
{
s.pop();
i++;
}
if(a[i]==cur)//如果希望驶出的车辆和原本顺序一样
{
cur++;//直接输出
i++;
}
else if(a[i]!=cur) //不是预期输出 ,那就进站
{
s.push(cur);
cur++;
}
else if(!s.empty() && s.top()>a[i])
{
flag =false;//不可能的
break;
}
}
if(flag)
{
cout << "Possible" << endl;
}
else
{
cout << "Impossible" << endl;
}
}
return 0;
}
9.奖学金评选【prize.cpp】
某大学正在评奖学金。候选人有 N 位(不超过 1000 人),取前 M 名。主要依据是他们平时 K 门(不 超过 100 门)必修课成绩,其中这 K 门必修课已按重要性从高到低排列好输入到了学生的个人档案中。在 更重要的科目取得更高分的学生排在前面。例如,A 第一重要的科目 96,第二门 89;B 第一门也是 96,第 二门 93。则按照规则,B 排在 A 的前面。为了避免获奖者偏科现象的发生,校长亲自指示获奖学生不能有 科目分数低于 85。现在将候选人编码 1~N,依次输入自己必修课的成绩(已按重要性降序排列),试求获 奖人员名单。(注意获奖的人数可能不足 M)
【输入样例】 7 3 2 93 92 89 96 87 93 93 96 94 79 88 93 91 97
//解释:第一行为候选人数 N、获奖人数 M 和必修课门数 K。
第二行至第(N+1)行,为编码 1~N 的 候选人必修课成绩记录(已按重要性降序排列)。
【输出样例】4 1 7 //解释:按排名由高到低输出获奖编号,用空格分隔。 【技巧提示】预处理时,如果有成绩<85,则做一标记,不参与排序;预处理时,应记录学生的编码。
#include<bits/stdc++.h>
using namespace std;
struct jiegou
{
int* chengji;
bool fuhe = true;
int bianhao = false;
};
int main()
{
int N, M, K; //N是候选人数 M是取前多少名发奖金 K是成绩有几门
cin >> N >> M >> K;
jiegou xuesheng[N];
for (int i = 0; i < N; i++)
{
xuesheng[i].bianhao = i + 1;
xuesheng[i].chengji = new int[K];
for (int j = 0; j < K; j++)
{
cin >> xuesheng[i].chengji[j];
if (xuesheng[i].chengji[j] < 85)
xuesheng[i].fuhe = false;
}
}
for (int i = 0; i < K; i++)
{
for (int a = 0; a < N; a++)
{
for (int b = a + 1; b < N; b++)
{
if (xuesheng[a].chengji[i] < xuesheng[b].chengji[i] )
{
if (i!=0)
{
if ( xuesheng[a].chengji[i-1] <= xuesheng[b].chengji[i-1] )
{
swap(xuesheng[a], xuesheng[b]);
}
}
else
swap(xuesheng[a], xuesheng[b]);
}
}
}
}
int mingci=0;
for (int i = 0; i < N; i++)
{
if (xuesheng[i].fuhe==1)
{
mingci++;
if (mingci==M)
{
cout<<xuesheng[i].bianhao;
}
}
}
return 0;
}
统计字符【cal.cpp】

$$
$$
#include<bits/stdc++.h>
using namespace std;
int cnt[26]; // 统计每个大写字母出现的次数
int main()
{
char s[100];
for (int i = 0; i < 4; i++)
{
gets(s); // 读入一行字符串
int len = strlen(s);
for (int j = 0; j < len; j++)
{
if (s[j] >= 'A' && s[j] <= 'Z') // 如果是大写字母,统计次数
{
cnt[s[j]-'A']++;
}
}
}
int max=0;
for (int i =0; i<26; i++)
{
if (cnt[i]>max)
{
max=cnt[i];
}
}
for (int i = max; i > 0; i--) // 输出柱状图,从上到下逐行输出 *
{
for (int j = 0; j < 26; j++)
{
if (cnt[j] >= i) // 如果该字母出现的次数大于等于当前行号,输出 *
{
cout << "* ";
}
else // 否则输出空格
{
cout << " ";
}
}
cout << endl;
}
for (int i = 0; i < 26; i++) // 输出字母和冒号
{
cout << char('A'+i) << " ";
}
cout << endl;
return 0;
}
匹配次数【match.cpp】

#include<bits/stdc++.h>
using namespace std;
int main()
{
char p[1000];
char s[1000];
gets(p);
gets(s);
int len_p=strlen(p);
int len_s=strlen(s);
int tmp =0;
int i =0;
int result=0;
for (tmp=0;tmp<=len_s-len_p;tmp++)
{
bool flag=true;
for (i=0;i<len_p;i++)
{
if (p[i]!=s[tmp+i])
flag=false;
}
if (flag)
result++;
}
cout<<result;
return 0;
}
/*
【输入样例】
aba
He abababa
【输出样例】
3
*/
后缀表达式计算

#include <bits/stdc++.h>
#include <stack>
using namespace std;
int main()
{
stack<double> st;
const int size=80;//限制表达式最长为79个字符
char buf[size];//存储表达式的输入缓冲区
gets(buf);
int i=0;
while(buf[i]!='@')
{
int a,b;
switch(buf[i])
{
case '+':
a=st.top();
st.pop();//先删除才能再取下一个
b=st.top();
st.pop();
st.push(a+b);
break;
case '-':
a = st.top();
st.pop();
b = st.top();
st.pop();
st.push(b - a);//后取出来的做被减数
break;
case '*':
a = st.top();
st.pop();//取出之后要删除才能取下一个
b = st.top();
st.pop();
st.push(a * b);
break;
case '/':
a = st.top();
st.pop();//取出之后要删除才能取下一个
b = st.top();
st.pop();
st.push(b / a);//后取出来的做被除数
break;
case ' ':
break;
default:
//说明是操作数要进栈,字符要转换成数值
if(int(buf[i-1]-'0')<=9&&int(buf[i-1]-'0')>=0 && i!=0)
{
a = st.top();
st.pop();//取出之后要删除才能取下一个
st.push(int(int(buf[i]-'0')+10*a));
}
else
st.push(int(buf[i]-'0'));
}
i++;
}
printf("%.6f\n",double(st.top()));
return 0;
}
pretree 前序遍历

#include<bits/stdc++.h>
using namespace std;
struct tNode
{
int id;//节点编号
int du;//结点的度数
tNode * zi[4];//孩子结点的数组,因为每一个孩子也有相对应的编号和度数,所以是tNdoe型
};
//前序遍历
void preOrder(tNode *p)
{
if(!p)
{
return;
}
cout<<p->id<<" ";
for(int i=0; i<p->du; i++)
{
preOrder(p->zi[i]);
}
}
int main()
{
int n;
cin>>n;
//先创建一棵树,动态分配内存
tNode *tree=new tNode[n+1];//因为树的编号是从1开始的
//按照编号往树中填充结点
for(int i=1; i<=n; i++)
{
int bianhao,du;
cin>>bianhao>>du;//先输入每个结点的编号和度
tree[bianhao].id=bianhao;
tree[bianhao].du=du;
//输入每个结点的子节点
for(int j=0; j<du; j++)
{
int son;
cin>>son;
tree[bianhao].zi[j]=&tree[son];//将子节点存储在父节点的孩子数组中
//因为数组中都是一些元素,而子节点都是一些指针,必须用取址符才能将子节点存进去
}
}
preOrder(tree+1);//因为第一个元素tree[0] 被置成空节点,树根是从tree[1]开始的
delete[] tree;//动态内存释放
return 0;
}
/*
输入:
5
1 3 2 3 4
2 1 5
3 0
5 0
4 0
输出:1 2 5 3 4
*/
一些常用的语法
memset

vector
typedef struct
<[(7条消息) 结构体定义 typedef struct 用法详解和用法小结_无敌的黑星星的博客-CSDN博客](https://blog.csdn.net/qq_41848006/article/details/81321883?ops_request_misc=%7B%22request%5Fid%22%3A%22167870866216800197010401%22%2C%22scm%22%3A%2220140713.130102334…%22%7D&request_id=167870866216800197010401&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_positive~default-2-81321883-null-null.142v73control_1,201v4add_ask,239v2insert_chatgpt&utm_term=typedef struct&spm=1018.2226.3001.4187)>
上标用:sup标签
例如:a<sup>10</sup>
结果为:a10
下标用:sub标签
例如:a<sub>10</sub>
结果为:a10
sort函数
<[[(9条消息) C++ Sort函数详解_zhangbw的博客-CSDN博客](https://blog.csdn.net/qq_41848006/article/details/81321883?ops_request_misc=%7B%22request%5Fid%22%3A%22167870866216800197010401%22%2C%22scm%22%3A%2220140713.130102334…%22%7D&request_id=167870866216800197010401&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_positivedefault-2-81321883-null-null.142v73control_1,201v4add_ask,239v2insert_chatgpt&utm_term=typedef struct&spm=1018.2226.3001.4187)>
(1)第一个是要排序的数组的起始地址。
(2)第二个是结束的地址(最后一位要排序的地址)
(3)第三个参数是排序的方法,可以是从大到小也可是从小到大,还可以不写第三个参数,此时默认的排序方法是从小到大排序。
没有参数时是从小到大;
若要实现从大到小排序:
//在外面定义一个complare函数
bool complare(int a,int b)
{
return a>b;
}
int main()
{
sort(a,a+10,complare);
//在这里就不需要对complare函数传入参数了,//这是规则
}
Sort函数使用模板
Sort(start,end,排序方法)
Sort函数的第三个参数可以用这样的语句告诉程序你所采用的排序原则
less<数据类型>()//从小到大排序
greater<数据类型>()//从大到小排序
sort(a, a+10 , less<int>() );//从小到大排序
sort(a, a+10 , greater<int>() );//从大到小排序
//还可对字符串排序,把<int>改成<char>即可
stack库 & queue库

第二章 顺序表
2.1线性表
n个元素组成的有限序列,k0,k1…kn-1,k0为开始结点,没有前驱,仅有一个后继,kn-1为终点,没有后继,仅一个前驱
2.1.1线性表的实现
#include <iostream>
using namespace std;
struct LinearList
{
int* data;//存数据的数组
int MaxSize;//最大空间
int count;//已有元素个数
};
void InitList(LinearList* L, int sz);//初始化
void FreeList(LinearList* L);//释放空间
bool ListEmpyt(LinearList* L);//判空
bool ListFull(LinearList* L);//判满
int ListLength(LinearList* L);//求表长
int GetElem(LinearList* L, int i);//读取第i个元素
int LocateElem(LinearList* L, int x);//确定元素x的位置
bool InsertElem(LinearList* L, int x, int i);// i位置插入新节点x
bool DeleteElem(LinearList* L, int i);//删去i位置的元素
void Reverse(LinearList* L);//将表倒置
bool huiwen(LinearList* L); //判断表是不是对称的
int main()
{
LinearList L;
int sz;
cin>>sz;
InitList(&L,sz);
}
void InitList(LinearList* L, int sz)
{
if(sz>0)
{
L->MaxSize=sz;
L->count=0;
L->data=new int[sz];//动态申请内存空间
}
}
void FreeList(LinearList* L)//释放空间
{
delete[]L->data;
}
bool ListEmpyt(LinearList* L)//判空
{
if(L->count <=0)
{
return true;
}
else
{
return false;
}
}
bool ListFull(LinearList* L)//判满
{
if(L->count >= MaxSize)
{
return true;
}
else
{
return false;
}
}
int ListLength(LinearList* L)//求表长
{
return L->count;
}
int GetElem(LinearList* L, int i)//读取第i个元素
{
//先判断有没有第i个元素
if(i<0 || i>=L->count)
{
return -1;
}
else
{
return L->data[i];
}
}
int LocateElem(LinearList* L, int x)//确定元素x的位置
{
for(int i=0;i<L->count;i++)
{
if(L->data[i]==x)
{
return i;
}
}
return -1;
}
bool InsertElem(LinearList* L, int x, int i)//i位置插入新节点x
{
//先判断是否有第i个位置
if(i<0 || i>L->count || L->count==L->MaxSize )
{
return false;
}
else
{
//i之后的元素都要后移
for(int j=L->count;j>i;j--)//倒着来,j是最后一个元素
{
L->data[j]=L->data[j-1];
}
L->data[i]=x;
L->count++;
return true;
}
}
bool DeleteElem(LinearList* L, int i)//删去i位置的元素
{
if(i<0 || i>L->count || L->count==L->MaxSize )
{
return false;
}
else
{
//从i开始(包括i)都要往前移
for(int j=i;j<L->count;j++)
{
L->data[j]=L->data[j+1];
}
L->count--;
return true;
}
}
void Reverse(LinearList* L)//将表倒置
{
//前一半的元素和后一半的元素交换
for(int i=0;i<L->count/2;i++)
{
int temp=L->data[i];
L->data[i]=L->data[L->count-i-1];
L->data[L->count - i -1] = tmp;
}
}
bool huiwen(LinearList* L) //判断表是不是对称的
{
for(int i=0;i<L->count;i++)
{
if(L->data[i]==L->data[L->count-i-1])
{
return true;
}
}
return false;
}
2.1.2求集合的并运算
struct Array
{
int* array;
int arraysize;
int arraylength;
};
int GetElem(Array* a, int i)//取值
{
if (i < 0 || i >= a->arraylength)
return -1;
else
return a->array[i];
}
void Union(LinearList* va, LinearList* vb)//集合并运算
{
int m= va->count;
int n= vb->count;
for(int i=0;i<m;i++)
{
int x=GetElem(vb, i);//x逐个取vb中的值
int k=LocateElem(va, x);//找x在va中的位置
if(k==-1)//没有找到,那就把x插入a
{
InsertElem(va, x, n);//将x插到va的尾部
n++;//长度要加一
}
}
}
2.1.3求集合的交运算
void Intersection(LinearList* va, LinearList* vb)
{
int m= va->count;
int n= vb->count;
int i=0;
while(i<m)
{
int x=GetElem(vb, i);//x逐个取vb中的值
int k=LocateElem(va, x);//找x在va中的位置
if(k==-1)//不在则删去
{
DeleteElem(vb, i);//删去vb中该元素
m--;
}
else
{
i++;
}
}
}
主函数
int main()
{
Array va, vb;//定义两个数组,即向量
int s1, s2;//两个数组的大小
cin >> s1 >> s2;
InitArray(&va, s1);
InitArray(&vb, s2);
int data1[10], data2[10];
//输入数据
for (int i = 0; i < 5; i++)
{
cin >> data1[i];
InsertElem(&va, data1[i], i);
}
for (int j = 0; j < 5; j++)
{
cin >> data2[j];
InsertElem(&vb, data2[j], j);
}
//求并集
Union(&va, &vb);
for (int i = 0; i < va.arraylength; i++)
cout << va.array[i] << " ";
cout << endl;
// 求交集
Intersection(&va, &vb);
for (int j = 0; j < vb.arraylength; j++)
cout << vb.array[j] << " ";
cout << endl;
return 0;
}
2.1.4约瑟夫问题
设n个人围成一个圆圈,按一指定方向,从第s个人开始报数,报数到m为止,报数为m的人出列,然后从下一个人开始从新报数,报数为m的人又出出列…,直到所有人全部出列为止。对任意给定的n,s,m,求按出列次序等到的人员顺序表
*求解思路:*先给这n个人编号,把n个数存入数组p中,某个人出列即把数组中对应元素删除,后面的元素前移,将删去的元素补至数组最后的位置,然后对前n-1个元素重复上述过程。
void Josephus(LinearList* L, int n, int s, int m)
{
int k=1;
for(int i=0;i<n;i++)//将人员编号存入数组L中
{
InsertElem(L,k,i);
k++;
}
int s1=s; //s1是s的后一个人 实际上是从s1-1开始报数的 因为数组从零开始存储 然后真实值和序号差1
for(int j=n;j>=1;j--)//j为当前剩余人数
{
s1=(s1-1+m)%j;//从s1-1位置开始报数,求出的是出列者的位置
if(s1==0)//此时需出列的是最后位置的人
s1==j;//因为是相差1
int w=GetElem(L,s1-1); //哪个位置的人应该出来
DeleteElem(L, s1 - 1);//删去这个位置的元素 即把这个人从队列里面拿出来 后面的元素前移
InsertElem(L, w, n - 1);//把删去的元素放到末尾
}
cout<<L->data[0];//留到最后的元素
}
2.3 栈-后进先出
基本内容
栈的插入和删除操作只允许在表尾一端进行,称之为栈顶
栈顶指针top,指向最后一个进栈的元素(指向an-1),取值为0-MaxSize-1
//栈空:top=-1;
//栈满:top=MaxSize-1;
2.3.1栈的代码实现
#include <iostream>
using namespace std;
class myStack
{
int *a;//存放栈元素的数组
int top;//实际上是下标,因为代表指向某元素,所以称为指针
int MaxSize;
public:
myStack(int sz)//构造函数
{
MaxSize=sz;
top=-1;
a=new int[MaxSize];
}
~myStack();
void clear();//置空
bool empty();//判空
bool full();//判满
bool push(int item);//压栈
bool pop();//出栈
int dutop();//读取栈顶元素
};
myStack::~myStack()
{
delete a;
}
void myStack::clear()
{
top=-1;
}
bool myStack::empty()
{
if(top==-1)
{
return true;
}
else
return false;
}
bool myStack::full()
{
if(top==MaxSize-1)
{
return true;
}
else
return false;
}
bool myStack::push(int item)//压栈
{
if(!full())
{
a[++top]=item;//top指向的是原来的最后一个元素,所以要先++top让它指向下一个位置,再把元素放进去
return true;
}
else
{
return false;
}
}
bool myStack::pop()//出栈
{
if(empty())
return false;
top--;
return true;
}
int myStack::dutop()
{
return a[top];
}
//--------------------------------测试------------------------------
int main()
{
myStack st(1000);//首先先建立一个这样子的栈
for(int i=0;i<=10;i++)
{
st.push(i);
}
while(!st.empty())
{
cout<<st.dutop()<<endl;
st.pop();
}
return 0;
}
2.3.2顺序栈的模板类
#include<bits/stdc++.h>
using namespace std;
template<class T>
class myStack
{
T *a;
int maxSize;
int top;
public:
myStack(int sz)//构造函数写进public
{
maxSize = sz;
top = -1;
a = new T[maxSize];
}
~myStack();
void clear();
bool empty();
bool full();
bool push(T x);
bool pop();
int dutop();
};
template<class T>
myStack<T>::~myStack()
{
delete a;
}
template<class T>
void myStack<T>::clear()
{
top = -1;
}
template<class T>
bool myStack<T>::empty()
{
return top == -1;
}
template<class T>
bool myStack<T>::full()
{
return top == maxSize - 1;
}
template<class T>
bool myStack<T>::push(T x)
{
if (!full())
{
a[++top] = x;//top是前++,top指向的位置已有元素要先加一再放元素
return true;
}
else
{
return false;
}
}
template<class T>
bool myStack<T>::pop()
{
if(empty()) return false;
top--;
return true;
}
template<class T>
int myStack<T>::dutop()
{
return a[top];
}
//测试模板栈
//int main()
//{
// myStack <int>st(1000);//int型的栈
// for (int i = 1; i <= 10; i++)
// st.push(i);
// while (!st.empty())
// {
// cout << st.dutop() << endl;
// st.pop();
// }
// return 0;
//}
2.3.3后缀表达式
基本内容
扫描,如遇到操作数则压栈,如遇操作符则将栈顶的两个元素弹出进行计算后将结果压栈
只需要一个栈
代码实现
int main()
{
//假设运算符只有+、-、*、/,操作数都是个位数
myStack st=myStack(80);
const int size=80;//限制表达式最长为79个字符
char buf[size];//存储表达式的输入缓冲区
cin>>buf;
int i=0;
while(buf[i]!='\0')
{
int a,b;
switch(buf[i])
{
case '+':
a=st.dutop();
st.pop();//先删除才能再取下一个
b=st.dutop();
st.pop();
st.push(a+b);
break;
case '-':
a = st.dutop();
st.pop();
b = st.dutop();
st.pop();
st.push(b - a);//后取出来的做被减数
break;
case '*':
a = st.dutop();
st.pop();//取出之后要删除才能取下一个
b = st.dutop();
st.pop();
st.push(a * b);
break;
case '/':
a = st.dutop();
st.pop();//取出之后要删除才能取下一个
b = st.dutop();
st.pop();
st.push(b / a);//后取出来的做被除数
break;
default:
//说明是操作数要进栈,字符要转换成数值
st.push(int(buf[i]-'0'));
}
i++;
}
cout << st.dutop() << endl;
return 0;
}
2.3.4中缀表达式
基本内容
当前扫到的运算符的优先级比前一个的低,那就计算前一个运算符
即:高则压栈,低则计算
注:)的优先级最低
关键在于处理好括号,保证括号内的运算能优先进行
用一个字符栈保存运算符、一个数字栈(这里采用vector动态数组,因为方便修改末尾元素)保存运算结果。
主要步骤
输入中缀表达式,从头开始遍历,若当前字符为开括号,直接入字符栈;
若当前字符为闭括号,不断弹出字符栈顶运算符,直到栈顶为开括号,将其弹出;
若当前字符为数字,将其转化成整型后压栈,
若当前字符opt为运算符** 比较opt和字符栈顶符号top,只要字符栈非空且栈顶元素不是开括号且优先级:top>=opt,就弹栈,然后同步弹出数字栈两个元素,做运算,结果再压回数字栈。结束以后把opt入字符栈。
**当前表达式遍历完后如果字符栈还有元素,要全部弹完,**一样是和数字栈的元素做运算,后者剩下的最后一个元素就是表达式的值。
代码实现
#include<iostream>
#include<stack>
#include<vector>
#include<string>
using namespace std;
int level(char a)//返回运算符的优先级
{
int lev=0;
if(a == '+' || a =='-')
{
lev=1;
}
else if (a == '*' || a == '/')
lev = 2;
return lev;
}
int cal(int x, int y, char opt) //四则运算
{
int ret=0;
if (opt == '+') ret = x + y;
else if (opt == '-') ret = x - y;
else if (opt == '*') ret = x * y;
else if (opt == '/') ret = x / y;
return ret;
}
void popcal(stack<char>& s,vector<int> &num)//弹栈,做运算,再存栈 s是运算符栈,num是数据栈
{
char opt=s.top();//读取栈顶的运算符
s.pop();
int x=num.back();//back函数:vector中返回 尾元素的函数
num.pop_back();//也是自带的
int y=num.back();
num.pop_back();
num.push_back(cal(x,y,opt));//运算结果压栈
}
int main()
{
stack<char> s;//运算符栈
vector<int> num;// 整数的动态数组(整数栈),最终剩下的一个数就是表达式的值
string infix;//中缀表达式
for(int i=0;i<infix.length();i++)//开始遍历表达式
{
if(infix[i]=='(')
{
s.push(infix[i]);//压栈
}
else if(infix[i]==')')
{
if(!s.empty())
{
while(s.top()!='(')
{
popcal(s,num);
}
s.pop();//把运算符中的'('弹出
}
}
else if (infix[i] == '+' || infix[i] == '-' || infix[i] == '*' || infix[i] == '/')
{
while(!s.empty() && s.top()!='(' && level(s.top())>=level(infix[i]))
{
popcal(s,num);
}
s.push(infix[i]);//若栈顶是'(',默认输入运算符优先级最高,直接压栈
}
else//扫描到数字时
{
int temp=infix[i]-'0';
num.push_back(temp);
}
}
while(!s.empty())
{
popcal(s,num);//符号栈为空才算完
}
int result=num.back();
cout<<result;
return 0;
}
2.3.5中缀表达式转后缀表达式
假定中缀表达式存放在向量E中,等价的后缀表达式存放在向量A中;使用栈Sptr,栈中的表目为字符型.
1)从左至右扫描向量E.遇操作数压入A;
遇左开括号‘(’和暂时不能确定计算次序的运算符压入Sptr;
遇‘+’,‘-’符,看栈顶元素,弹出栈顶的非‘(’元素A,遇到的‘+’,‘-’ 压入Sptr;
遇‘* ’ ,‘ /’符,依次看栈Sptr中的元素,仅当栈顶元素为‘ * ’,‘ /’ 时弹栈压入A, 再将遇到的‘*’,‘/’ 压 入Sptr;
遇‘)’时,依次弹出栈顶的运算符直到弹出一个‘(’为止.
2)若中缀表达式已扫描完,而栈中还有运算符,则依次弹出栈顶的运算符压入A.
//没有考虑次方运算
//输入只能是数字和运算符号
#include<bits/stdc++.h>
#include<stack>
using namespace std;
//中缀转后缀
int main()
{
stack<char >operators;
string s;
getline(cin, s);
int i = 0;
string str;
while (s[i] != '\0')
{
//如果是数字
if (s[i] >= '0' && s[i] <= '9')
{
string num;
num += s[i];
//考虑数字位数不止一位
while ((s[i + 1] >= '0' && s[i + 1] <= '9') || s[i + 1] == '.')
{
num += s[++i];
}
str += num+' ';
}
else if (s[i] == ' ')
{
}
//否则是符号
else
{
char c = s[i];
if (c == '(')
{
operators.push(c);
}
else if (c == ')')
{
while (!operators.empty() && operators.top() != '(')
{
char s1 = operators.top();
str += s1;
operators.pop();
}
operators.pop();
}
else if (c == '*' || c == '/')
{
if (!operators.empty() && (operators.top() == '*' || operators.top() == '/'))
{
char s1 = operators.top();
str += s1;
operators.pop();
}
operators.push(c);
}
else if (c == '+' || c == '-')
{
while (!operators.empty() && operators.top() != '(') //top()的使用必须保证栈顶不为空 ,因此先判断empty()
{
char s1 = operators.top();
str += s1;
operators.pop();
}
operators.push(c);
}
}
i++;
}
while (!operators.empty())
{
char s1 = operators.top();
str += s1;
operators.pop();
}
cout << str << endl;
return 0;
}
/*
样例
输入样例
中缀:
(1+1*2)*1+3*2/1
输出样例
后缀:
1 1 2 * + 1 * 3 2 * 1 / +
*/
2.4队列-先进先出
2.4.1简单队列
基本内容
插入操作只允许在表尾,删除操作只允许在表头
允许插入的一端叫做队尾,允许删除的一端叫做队头
队头指针front,指向队头元素;队尾指针rear,指向即将入队的元素,即尾的下一个元素
代码实现
#include <iostream>
using namespace std;
struct cQueue
{
int *a;
int MaxSize;
int front,rear;//实际上是下标,因为代表指向某元素,所以称为指针
};
//初始化
void init(cQueue *q,int sz) //定义了一个队列q
{
q->a=new int[sz];//存队列中的元素
q->MaxSize=sz;
q->front=q->rear=0;
}
//释放空间
void flush(cQueue *q)
{
delete q->a;
}
//判空
bool empty(cQueue *q)
{
if(q->front==q->rear)
{
return true;
}
}
//判满
bool full(cQueue *q)
{
if(q->rear==q->MaxSize) //因为rear指向的是即将入队的元素的下标,如果==MaxSize,那说明 已经有MaxSize-1个元素了,已经满了
{
return true;
}
}
//清空
void clear(cQueue *q)
{
q->front=q->rear=0;
}
//求队长
int size(cQueue *q)
{
return q->rear - q->front;
}
//插入x
bool push(cQueue *q,int x)
{
if(full(q))
return 0;
q->a[q->rear++]=x;//?
return 1;
}
//删除队头元素
void pop(cQueue *q)
{
q->front++;
}
//读取队头元素
int front(cQueue *q)
{
return q->a[q->front];
}
//测试队列
int main()
{
cQueue q;
init(&q,100);
for(int i=0;i<=10;i++)
{
push(&q,i);
}
cout<<size(&q)<<endl;
while(size(q))
{
cout<<front(&q)<<" ";
pop(&q);//从队头开始输出一个删除一个
}
}
2.4.2循环队列
关键点:最多只能存储MaxSize-1个元素
size=(rear-front+maxsize)%maxsize;
入队:push(x):
a[rear++]=x;
rear=%maxsize;
出对:pop:
front++;
front %= maxsize;
代码实现
#include <iostream>
using namespace std;
class cQueue
{
int head;
int rear;
int maxSize;
int *a;
public:
void init(int sz);//初始化
bool empty();
bool full();
int size();//求队长
void push(int x);//队尾插入元素
void pop();//删除队头元素
int front(); //读取队头
} ;
void cQueue::init(int sz)
{
head = rear = 0;
maxSize = sz;
a = new int[sz];
}
bool cQueue::empty()
{
return head == rear;
}
bool cQueue::full()
{
//rear即将追上head
return head == (rear+1)%maxSize;//?
}
int cQueue::size()
{
return (rear-head+maxSize)%maxSize;
}
void cQueue::push(int x)
{
a[rear++] = x;
rear = rear % maxSize;
//循环队列
}
void cQueue::pop()
{
head++;
head = head%maxSize;
}
int cQueue::front()
{
return a[head];
}
//循环队列的测试
//int main()
//{
// cQueue q;
// q.init(20);
// for (int i = 1; i <=15; i++)
// {
// q.push(i);
// }
// while (q.size())
// {
// cout << q.front() << " ";
// q.pop();
// }
// return 0;
//}
求解舞伴问题
//周末舞会上,男士们女士们进入舞厅时,各自排成一队。跳舞开始时,依次从男队和女队的队头上各处一人配成舞伴。
//规定每首舞曲只能有一对跳舞者。若两队初始人数不相同,则较长的那一队中为配对者等待下一轮舞曲开始。
int main()
{
int man, lady, m;//男士、女士的人数,舞曲数
cQueue qM,qL;//男士、女生的队列
cin >> man >> lady >> m;
qM.init(1000);
qL.init(1000);
//将男士女士加入队列
for (int i = 1; i <= man; i++)
qM.push(i);
for (int i = 1; i <= lady; i++)
qL.push(i);
for (int i = 1; i <= m; i++)
{
int a, b;
a = qM.front();//a从头开始
qM.pop();//删去队头,即为出去的舞者
qM.push(a);//再将刚刚出去的舞者放入队尾
b = qL.front();
qL.pop();
qL.push(b);
cout<<a<<" "<<b<<endl;
}
return 0;
}
求解约瑟夫问题–用队列实现
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
queue<int >q;//用q队列来存放这n个人
int k=0;//报的该数
for(int i=0;i<n;i++)
{
q.push(i);
}
int temp;
while(q.size())
{
k++;
temp=q.front();//取队头的元素
q.pop();
if(k==m)//当报到m时
{
cout<<temp <<" ";
k=0;//将k置零
}
else
{
q.push(temp);
}
}
return 0;
}
2.4.3优先级队列
#include <iostream>
using namespace std;
#define maxSize 50
class PQueue
{
private:
int pqlist[maxSize];
int count;
public:
PQueue();
~PQueue(){delete pqlist;}
void PQInsert(int item);
int PQDelete();
void ClearPQ();
int PQEmpty();
int PQFull();
int PQLength();
};
PQueue::PQueue()
{
count = 0;
}
void PQueue::PQInsert(int item)
{
//优先级存储空间是否已满
if (count == maxSize)
{
cout << "已满" << endl;
return;
}
pqlist[count] = item;
count++;
}
int PQueue::PQDelete()
{
//找最小优先级
int min;
int i, minindex = 0;
if (count > 0)
{
//找最小优先级
min = pqlist[0];
for (i = 1; i < count; i++)
{
if (pqlist[i] < min)
{
min = pqlist[i];
minindex = i;
}
}
//替换最小元素
pqlist[minindex] = pqlist[count - 1];
count--;
}
//若优先级为空算法结束
else
{
cout << "优先级已空" << endl;
return NULL;
}
return min;
}
void PQueue::ClearPQ()
{
count = 0;
}
int PQueue::PQEmpty()
{
return count == 0;
}
int PQueue::PQFull()
{
return count == maxSize;
}
int PQueue::PQLength()
{
return count;
}
int main()
{
PQueue q;
int n;
for (int i = 0; i < 10; i++)
{
cin >> n;
q.PQInsert(n);
}
cout << q.PQDelete() << endl;
return 0;
}
第三章 链表
3.1单链表
3.1.1单链表结点类
//苏佳慧版
//节点类
template<class T>
class Node
{
public:
T data;//数据域
Node<T>* next;//指针域
//构造函数1
Node()
{
next = NULL;
}
//构造函数2
Node(const T& item)
{
data = item;
next = NULL;
}
~Node();//析构函数
//获取下一节点指针
Node<T> *NextNode() const;
//删除结点
Node *DeleteAfter()
{
//保存当前节点的后继结点
Node<T> *ptr = next;
//若没有后继结点返回空指针
if (ptr == NULL)
return NULL;
//当前结点指向其原来后继的后继,即ptr的后继
next = ptr->next;
//返回被删除结点的指针
return ptr;
}
//得到该结点的值
Node<T> *getdata()const
{
return data;
}
};
//佟亚龙版//-----------------------------------------------链表类 -----------------------------------------------------------
template<class T>
class LinkedList
{
private:
Node<T> *front, *rear, *head, *ptr;//指向表头、表尾的指针
Node<T> *cur, *pre;//用于指向当前和前一个结点的指针
int size;//当前节点个数
int position;//当前位置
//申请及释放单链表结点空间的函数
Node<T> *GetNode(const T& item, Node<T> *ptr = NULL);
void FreeNode(Node<T> * p);
public:
LinkedList();//构造函数
~LinkedList();//析构函数
//重载的赋值运算符
LinkedList<T>& operator = (const LinkedList<T> & orgList);
//获取单链表的结点个数
int Size() const;
//判断单链表是否为空
bool empty()const;
//重新定位当前单链表结点
int NextNode();
int SetPosition(int pos);
int GetPosition() const;
//插入结点
void InsertAfter(const T& item);//当前位置之后插入节点
void InsertAt(const T& item); //就在当前位置插入节点
//删除链表结点的函数
void DeleteAt();
void DeleteAfter();
//修改和访问数据的函数
T GetData()const;
void SetData (const T& item);
//清空链表的函数
void Clear();
};
//申请及释放单链表结点空间的函数
template<class T>
Node<T> *LinkedList<T>::*GetNode(const T& item, Node<T> *ptr = NULL)
{
Node<T> *newNode = new Node<T>(item, ptr);
//若动态内存申请失败则给出相应的提示并返回空指针
if(!newNode)
{
cout << "申请失败" <<endl;
return NULL;
}
//返回新生成的结点指针
return newNode;
}
template<class T>
void LinkedList<T>::FreeNode(Node<T> * p)
{
//若ptr为空,给出相应提示并返回
//####if(!ptr)
if(!p)
{
cout << "FreeNode error!" << endl;
return;
}
//释放结点占用的内存空间
//####delete ptr;
delete p;
return;
}
//构造函数 (建立一个空链表)
template<class T>
LinkedList<T>::LinkedList()
{
//####head = pre = new Node<T>(0,NULL);//附加头结点
head = pre = new Node<T>(0);
front = rear = NULL;
cur = NULL;
size = 0;
position = -1;
}
//析构函数
template<class T>
LinkedList<T>::~LinkedList()
{
//清空单链表,释放所有的结点空间
Clear();
}
//单链表类中重载赋值运算符的函数
template<class T>
LinkedList<T>& LinkedList<T>::operator = (const LinkedList<T>& orgList)
{
Node<T> *p = orgList.front;
//清空本链表
Clear();
//将单链表 orgList中的元素复制到本单链表
while(p)
{
InsertAfter(p->data);
p = p->NextNode();
}
//设置当前结点
SetPosition(orgList.position);
return *this;
}
//获取表的大小
template<class T>
int LinkedList<T>::Size() const
{
return size;
}
//判断表是否为空
template<class T>
bool LinkedList<T>::empty() const
{
if (size == 0)
return true;
else
return false;
}
//将后继结点设置为当前结点的函数
template<class T>
int LinkedList<T>::NextNode()
{
//若当前结点存在,则将其后继结点设置为当前节点
if (position >= 0 && position < size)
{
position++;
pre = cur;
//####cur = cur->NextNode();
cur = cur->next;
}
else//否则将当前位置设为表尾
{
position++;
}
return position;//返回新位置
}
//重置当前结点的位置
template<class T>
int LinkedList<T>::SetPosition(int pos)
{
if (!size)//若链表为空
return -1;
if (pos < 0 ||pos > size - 1)
{
cout << "越界" << endl;
return -1;
}
pre = NULL;
cur = front;
position = 0;
for (int k = 0; k < pos; k++)
{
position++;
pre = cur;
cur = cur->next;
}
return position;//返回当前结点的位置
}
//取出当前结点位置
template<class T>
int LinkedList<T>::GetPosition() const
{
return position;
}
//在当前结点后插入结点
template<class T>
void LinkedList<T>::InsertAfter(const T& item)
{
//####Node<T> *p = new Node<T>(item, NULL);
Node<T> *p = new Node<T>(item);
if (!cur)//空链表
{
head->next = p;
rear = p;
//####此处加入设置front指针
front = p;
}
else
{
p->next = cur->next;//不考虑位置:头、中间、尾
cur->next = p;
if (!p->next)//当前位置是链尾
rear = p;
}
size++;
cur = p;//cur指向新结点
}
//在当前结点处插入新的结点
template<class T>
void LinkedList<T>::InsertAt(const T& item)
{
Node<T> *p = new Node<T>(item);
p->next = cur;
pre->next = p;
cur = p;
size++;
if (!rear)//尾结点为空,说明是空链
{
rear = p;
//####此处加入设置front指针
front = p;
}
}
//删除当前结点
template<class T>
void LinkedList<T>::DeleteAt()
{
Node<T> *oldNode;
if(!cur)//若链表为空或已经到达表尾
{
cout << "DeleleAt:current position is invalid!" << endl;
return;
}
if (!pre)//说明要删除的是表头结点
{
oldNode = front;
front = cur->next;
}
else//说明要删除的是表中结点
{
oldNode = pre->DeleteAfter();
}
if (oldNode == rear)//删除表尾结点,则修改表尾指针
{
rear = pre;
}
cur = oldNode->next;//后继结点作为新的结点
FreeNode(oldNode);//释放当前结点
size--;//链表大小减一
}
//删除当前结点后继
template<class T>
void LinkedList<T>::DeleteAfter()
{
Node<T> *oldNode;
if (!cur || cur == rear)//若无当前结点或者已经到达链表尾
{
cout << "DeleteAfter:current position in invalid!" << endl;
return;
}
oldNode = cur->DeleteAfter();//保存被删除的结点指针并删除该节点
if (oldNode == rear)//删除的是表尾结点
{
rear = cur;
}
FreeNode(oldNode);
}
//获取当前结点数据
template<class T>
//####T LinkedLlist<T>::GetData() const
T LinkedList<T>::GetData() const
{
if (!cur)//若链表为空或已经到达表尾
{
cout << "Data:current node not exist!" << endl;
return NULL;
}
return cur->data;
}
//修改当前结点数据
template<class T>
//####void LinkedList<T>::Setdata(const T& item)
void LinkedList<T>::SetData(const T& item)
{
if (!cur)//若链表位空或已经到达表尾
{
cout << "Data:current node does not exist!" << endl;
return;
}
cur->data = item;//修改当前结点的数据
}
//清空链表
template<class T>
void LinkedList<T>::Clear()
{
Node<T> *cur = front, *nextNode;
while (cur)
{
nextNode = cur->next;//保存后继结点指针
FreeNode(cur);//释放当前结点
cur = nextNode;//原后继结点成为当前结点
}
//修改链表数据
front = rear = pre = cur = NULL;
size = 0;
position = -1;
}
int main()
{
LinkedList<int> L;
for (int i = 0; i<=10; i++)
{
L.InsertAfter(i);
}
// 在第五个位置插入666
L.SetPosition(5);
L.InsertAt(666);
L.SetPosition(0);//将当前结点调回头结点
cout << "LinkedList: " << endl;
while(L.NextNode() != L.Size())
{
cout <<L.GetData() << " ";
}
cout << endl;
}
实现插入结点
#include <iostream>
using namespace std;
template<class T>
class Node
{
public:
T data;//数据域
Node<T>* next;//指针域
//构造函数1
Node()
{
next = NULL;
}
//构造函数2
Node(const T& item)
{
data = item;
next = NULL;
}
//获取下一节点指针
Node<T> *NextNode() const;
//删除结点
Node *DeleteAfter()
{
//保存当前节点的后继结点
Node<T> *ptr = next;
//若没有后继结点返回空指针
if (ptr == NULL)
return NULL;
//当前结点指向其原来后继的后继,即ptr的后继
next = ptr->next;
//返回被删除结点的指针
return ptr;
}
//得到该结点的值
T getdata(Node *p)
{
return p->data;
}
//在当前结点后插入一个结点
void InsertAfter(Node<T> *p)
{
//将当前结点的后继结点连接到结点p之后
p->next = next;
//将p作为当前节点的后继结点
next = p;
}
};
int main()
{
Node<int> nd1(100), nd2(200), nd3(300), *p;
nd1.InsertAfter(&nd2);
nd1.InsertAfter(&nd3);
p = &nd1;
while (p)
{
cout <<p->data<<" ";
p = p->next;
}
cout << endl;
return 0;
}
3.1.2单链表链表类
#include<bits/stdc++.h>
using namespace std;
//节点类
template<class T>
class Node
{
public:
T data;//数据域
Node<T>* next;//指针域
//构造函数1
Node()
{
next = NULL;
}
//构造函数2
Node(const T& item)
{
data = item;
next = NULL;
}
//获取下一节点指针
Node<T> *NextNode() const;
//删除结点
Node *DeleteAfter()
{
//保存当前节点的后继结点
Node<T> *ptr = next;
//若没有后继结点返回空指针
if (ptr == NULL)
return NULL;
//当前结点指向其原来后继的后继,即ptr的后继
next = ptr->next;
//返回被删除结点的指针
return ptr;
}
//得到该结点的值
Node<T> *getdata()const
{
return data;
}
};
//-----------------------------------------------链表类 -----------------------------------------------------------
template<class T>
class LinkedList
{
private:
Node<T> *front, *rear, *head, *ptr;//指向表头、表尾的指针
Node<T> *cur, *pre;//用于指向当前和前一个结点的指针
int size;//当前节点个数
int position;//当前位置
//申请及释放单链表结点空间的函数
Node<T> *GetNode(const T& item, Node<T> *ptr = NULL);
void FreeNode(Node<T> * p);
public:
LinkedList();//构造函数
~LinkedList();//析构函数
//重载的赋值运算符
LinkedList<T>& operator = (const LinkedList<T> & orgList);
//获取单链表的结点个数
int Size() const;
//判断单链表是否为空
bool empty()const;
//重新定位当前单链表结点
int NextNode();
int SetPosition(int pos);
int GetPosition() const;
//插入结点
void InsertAfter(const T& item);//当前位置之后插入节点
void InsertAt(const T& item); //就在当前位置插入节点
//删除链表结点的函数
void DeleteAt();
void DeleteAfter();
//修改和访问数据的函数
T GetData()const;
void SetData (const T& item);
//清空链表的函数
void Clear();
};
//申请及释放单链表结点空间的函数
template<class T>
Node<T> *LinkedList<T>::*GetNode(const T& item, Node<T> *ptr = NULL)
{
Node<T> *newNode = new Node<T>(item, ptr);
//若动态内存申请失败则给出相应的提示并返回空指针
if(!newNode)
{
cout << "申请失败" <<endl;
return NULL;
}
//返回新生成的结点指针
return newNode;
}
template<class T>
void LinkedList<T>::FreeNode(Node<T> * p)
{
//若ptr为空,给出相应提示并返回
//####if(!ptr)
if(!p)
{
cout << "FreeNode error!" << endl;
return;
}
//释放结点占用的内存空间
//####delete ptr;
delete p;
return;
}
//构造函数 (建立一个空链表)
template<class T>
LinkedList<T>::LinkedList()
{
//####head = pre = new Node<T>(0,NULL);//附加头结点
head = pre = new Node<T>(0);
front = rear = NULL;
cur = NULL;
size = 0;
position = -1;
}
//析构函数
template<class T>
LinkedList<T>::~LinkedList()
{
//清空单链表,释放所有的结点空间
Clear();
}
//单链表类中重载赋值运算符的函数
template<class T>
LinkedList<T>& LinkedList<T>::operator = (const LinkedList<T>& orgList)
{
Node<T> *p = orgList.front;
//清空本链表
Clear();
//将单链表 orgList中的元素复制到本单链表
while(p)
{
InsertAfter(p->data);
p = p->NextNode();
}
//设置当前结点
SetPosition(orgList.position);
return *this;
}
//获取表的大小
template<class T>
int LinkedList<T>::Size() const
{
return size;
}
//判断表是否为空
template<class T>
bool LinkedList<T>::empty() const
{
if (size == 0)
return true;
else
return false;
}
//将后继结点设置为当前结点的函数
template<class T>
int LinkedList<T>::NextNode()
{
//若当前结点存在,则将其后继结点设置为当前节点
if (position >= 0 && position < size)
{
position++;
pre = cur;
//####cur = cur->NextNode();
cur = cur->next;
}
else//否则将当前位置设为表尾
{
position++;
}
return position;//返回新位置
}
//重置当前结点的位置
template<class T>
int LinkedList<T>::SetPosition(int pos)
{
if (!size)//若链表为空
return -1;
if (pos < 0 ||pos > size - 1)
{
cout << "越界" << endl;
return -1;
}
pre = NULL;
cur = front;
position = 0;
for (int k = 0; k < pos; k++)
{
position++;
pre = cur;
cur = cur->next;
}
return position;//返回当前结点的位置
}
//取出当前结点位置
template<class T>
int LinkedList<T>::GetPosition() const
{
return position;
}
//在当前结点后插入结点
template<class T>
void LinkedList<T>::InsertAfter(const T& item)
{
//####Node<T> *p = new Node<T>(item, NULL);
Node<T> *p = new Node<T>(item);
if (!cur)//空链表
{
head->next = p;
rear = p;
//####此处加入设置front指针
front = p;
}
else
{
p->next = cur->next;//不考虑位置:头、中间、尾
cur->next = p;
if (!p->next)//当前位置是链尾
rear = p;
}
size++;
cur = p;//cur指向新结点
}
//在当前结点处插入新的结点
template<class T>
void LinkedList<T>::InsertAt(const T& item)
{
Node<T> *p = new Node<T>(item);
p->next = cur;
pre->next = p;
cur = p;
size++;
if (!rear)//尾结点为空,说明是空链
{
rear = p;
//####此处加入设置front指针
front = p;
}
}
//删除当前结点
template<class T>
void LinkedList<T>::DeleteAt()
{
Node<T> *oldNode;
if(!cur)//若链表为空或已经到达表尾
{
cout << "DeleleAt:current position is invalid!" << endl;
return;
}
if (!pre)//说明要删除的是表头结点
{
oldNode = front;
front = cur->next;
}
else//说明要删除的是表中结点
{
oldNode = pre->DeleteAfter();
}
if (oldNode == rear)//删除表尾结点,则修改表尾指针
{
rear = pre;
}
cur = oldNode->next;//后继结点作为新的结点
FreeNode(oldNode);//释放当前结点
size--;//链表大小减一
}
//删除当前结点后继
template<class T>
void LinkedList<T>::DeleteAfter()
{
Node<T> *oldNode;
if (!cur || cur == rear)//若无当前结点或者已经到达链表尾
{
cout << "DeleteAfter:current position in invalid!" << endl;
return;
}
oldNode = cur->DeleteAfter();//保存被删除的结点指针并删除该节点
if (oldNode == rear)//删除的是表尾结点
{
rear = cur;
}
FreeNode(oldNode);
}
//获取当前结点数据
template<class T>
//####T LinkedLlist<T>::GetData() const
T LinkedList<T>::GetData() const
{
if (!cur)//若链表为空或已经到达表尾
{
cout << "Data:current node not exist!" << endl;
return NULL;
}
return cur->data;
}
//修改当前结点数据
template<class T>
//####void LinkedList<T>::Setdata(const T& item)
void LinkedList<T>::SetData(const T& item)
{
if (!cur)//若链表位空或已经到达表尾
{
cout << "Data:current node does not exist!" << endl;
return;
}
cur->data = item;//修改当前结点的数据
}
//清空链表
template<class T>
void LinkedList<T>::Clear()
{
Node<T> *cur = front, *nextNode;
while (cur)
{
nextNode = cur->next;//保存后继结点指针
FreeNode(cur);//释放当前结点
cur = nextNode;//原后继结点成为当前结点
}
//修改链表数据
front = rear = pre = cur = NULL;
size = 0;
position = -1;
}
int main()
{
LinkedList<int> L;
for (int i = 0; i<=10; i++)
{
L.InsertAfter(i);
}
// 在第五个位置插入666
L.SetPosition(5);
L.InsertAt(666);
L.SetPosition(0);//将当前结点调回头结点
cout << "LinkedList: " << endl;
while(L.NextNode() != L.Size())
{
cout <<L.GetData() << " ";
}
cout << endl;
}
3.1.3单链表实现栈和队列
#include<bits/stdc++.h>
using namespace std;
template <class T>
class cNode//结点类
{
public:
T data;
cNode<T> *next;
cNode(const T& item)
{
data = item;
next = NULL;
}
~cNode(){}
};
template <class T>
class cStack//栈
{
cNode<T> *front;
int count;
public:
cStack()
{
front = NULL;
count = 0;
}
~cStack()
{
clear();
}
void push(T x)
{
cNode<T> *p = new cNode<T>(x);//先创建一个新的结点
p->next = front;//新的结点指向front
front = p;//新的front改为p
count++;
}
void pop()
{
cNode<T> *p = front;
if (p)//p要是非空
{
count--;
front = front->next;
delete p;
}
}
T top()//读取栈顶元素
{
return front->data;
}
bool empty()
{
if(count == 0)
return true;
else
return false;
}
void clear()
{
cNode<T> *p = front;
while(p)//只要p不是空,说明还没清空
{
cNode<T> *t = p;//先将p储存下来
p = p->next;
delete t;
}
count = 0;
}
int size()
{
return count;
}
};
template<class T>
class cQueue//队列
{
cNode<T> *front, *rear;
int count;//元素个数
public:
cQueue()//构造函数
{
front = rear = 0;
count = 0;
}
~cQueue()//析构函数
{
clear();
}
//入队
void push(T x)
{
cNode<T> *p = new cNode<T>(x);
count++;
if (!rear)//rear不存在,是空链表
front = rear = p;
else
{
rear->next = p;
rear = p;
}
}
//出队
void pop()
{
cNode<T> *p = front;
count--;
front = front->next;
if (!front)//是空队列
rear=NULL;
delete p;
}
//读取队首元素
T top()
{
return front->data;
}
//判空
bool empty()
{
return !count;
}
//求队长
int size()
{
return count;
}
//清空队列
void clear()
{
cNode<T> *p = front;
while(p)
{
cNode<T> *t = p;
p = p->next;
delete t;
}
count = 0;
}
};
int main()
{
cStack<int> st;
cQueue<int> q;
for (int i = 1; i <= 10; i++)
{
st.push(i);
}
cout <<"栈的元素个数是:" << st.size()<<endl;
while (!st.empty())
{
cout << st.top() << endl;
st.pop();
}
cout << endl;
for (int i = 1; i <= 10; i++)
{
q.push(i);
}
cout << "队列的元素个数是:" << q.size() << endl;
while (!q.empty())
{
cout << q.top() << endl;
q.pop();
}
return 0;
}
第四章 排序
4.1插入排序
4.1.1直接插入排序
关键在于空位的处理
将第一个看做是排好的,从第二个开始排,
将待排序的放入temp

#include<bits/stdc++.h>
using namespace std;
template <class T>
void DirecInsSort(T* a, int n)
{
int i,j,p;//p为空位置
for(i=1;i<n;i++)//默认第一个排好,所以从1开始
{
int temp=a[i];//先把a[i]放入temp;那么i位置就空了
p=i;
for(j=i-1;j>=0;j--)//依次比较a[i-1,i-2....0]
{
if(temp<a[j])
{
a[p]=a[j];//把j放入之前的空位置,那么j就变成了空位置
p=j;
}
else
{
break;
}
}
a[p]=temp;
}
}
//---------------测试
int main()
{
int a[5];
for (int i =0;i<5;i++)
{
cin>>a[i];
}
DirecInsSort<int>(a, 5);
for (int i =0;i<5;i++)
{
cout<<a[i]<<" ";
}
}
4.1.2折半插入排序
#include<bits/stdc++.h>
using namespace std;
//折半插入
void BinInsSort(int *a,int n)
{
int i,L,R;//L和R是下标
for (int i =1; i<n; i++)//依次插入第1到第n个元素
{
int temp=a[i];
L=0;
R=i-1;
while(L<=R)//条件
{
int m =(L+R)/2;
if (temp<a[m])//在m之前插入
R=m-1;
else//在m之后找插入点
{
L=m+1;
}
}
//当L>R之后,L就是要找的插入点
for (R=i; R>L; R--)
{
a[R]=a[R-1];//相当于从最后一个也就是i位置到L之后的元素都要向后挪一个
}
a[L]=temp;//L位置就是要插入的元素
}
}
//------------------------
int main()
{
int a[10]={0};
a[1]=2;
a[2]=112;
a[6]=9;
BinInsSort(a,10);
for(int i=0; i<10; i++)
cout<<a[i]<<" ";
}
4.1.3 shell排序
#include<bits/stdc++.h>
using namespace std;
//shell排序
void ShellSort(int *a,int n)//n是元素个数 eg: 28 13 72 85 39 41 6 20
{
int i,j,h;
int s,temp;//s是组数
int x=0;
for(s=n/2; s>=1; s=s/2)//第一层循环是组数 每完成一次,就让当前组数再/2得下一次的组数 eg:第一次s=4
{
for(i=s;i<n;i++) //第二层循环是组的编号(每一组里的靠后的元素),所以i=s 第一次i=s=4-> 39 第二次 i=5-> 41
{
temp=a[i]; //组中后面的元素 第一次temp=39 第二次temp=41
j=i-s;//组中前面的元素
//第一次4-4=0; ->a[j]=28 第二次 temp=5-4=1 ->a[1]=13
while(j>=0 && temp<a[j])//对于每一个组进行插入排序
{
a[j+s]=a[j];
j=j-s;
}
a[j+s]=temp;
}
}
}
//--------------------------------
int main()
{
int a[10]={0};
a[1]=2;
a[2]=112;
a[6]=9;
ShellSort(a,10);
for(int i=0;i<10;i++)
cout<<a[i]<<" ";
}
4.2选择排序
4.2.1直接选择排序
#include<bits/stdc++.h>
using namespace std;
//直接选择排序--从待排序中选出最小的放在已排序的后面
void DirectSelectSort(int A[],int n)
{
int i,j,k;
int temp;
for(i=0;i<n-1;i++)//共有n-1次
{
k=i;//用k来存最小的那个数的角标
for(j=i+1;j<n;j++)
{
if(A[j]<A[k])//如果j比i小
{
k=j;
}
}
if(i!=k)//如果i不是最小的,最小的是k,那就把k放在最前面
{
temp=A[k];
A[k]=A[i];
A[i]=temp;
}
}
}
//---------------------------------------------
int main()
{
int a[10]={0};
a[1]=2;
a[2]=112;
a[6]=9;
DirectSelectSort(a,10);
for(int i=0;i<10;i++)
cout<<a[i]<<" ";
}
4.2.2树形选择排序
#include<bits/stdc++.h>
using namespace std;
//树形排序:从小到大(可能需要更改一下编译器的位数)
template<class T>
void treeSort(T* a, int n)
/* 对a[0 : n-1]进行树形选择排序。
返回后a[0 : n-1]为从小到大排序结果。
*/
{
#define Left(i) (2*(i)-2*n)
#define Right(i) (2*(i)-2*n+1)
#define Father(i) (n+(i)/2)
//#define Brother(i) ((i)&1 ? (i)-1:(i)+1)
#define Root (2*n-2)
#define min(a,b) (a)<(b)?(a):(b)
#define INF_VALUE 0x3FFFFFFF
T* t = new T(2*n-1);
memcpy(t, a, sizeof(T)*n);
//第1轮选择
for(int i=n; i<=Root; i++)
t[i]= min(t[Left(i)],t[Right(i)]);
a[0]=t[Root];
//第2轮至第n轮选择
for(int k=1; k<=n-1; k++)
{ // 将上一轮的最小值修改为无穷大INF_VALUE。
// 沿着等于t[Root]的分枝向下直到叶结点t[sel]=t[Root]
int sel=Root;
int left=Left(sel);
while(left>=0) // 判断sel是否为叶节点
{
sel = (t[sel]==t[left]) ? left : (left+1);
left=Left(sel);
}
t[sel]=INF_VALUE;
// 本轮选择:从叶往根从t[sel]往t[Root]选择最小值
sel=Father(sel);
while(sel<=Root)
{
t[sel] = min(t[Left(sel)],t[Right(sel)]);
sel = Father(sel);
}
a[k]=t[Root];
}
delete t;
}
//---------------------------------
int main()
{
int a[10]={0,45,723,23,3,45,5,8,9,12345};
treeSort(a, 10);
for(int i=0; i<10; i++)
cout<<a[i]<<" ";
return 1;
}
4.3交换排序
4.3.1快速排序!!!(重点)
从待排记录中任意选一个记录,左边的和这个比,找到比他大的拿出来,右边的和这个比,比他小的拿出来,然后把拿出的两个交换,然后循环操作,直到左边界等于右边界
#include <bits/stdc++.h>
using namespace std;
void swap(int &a, int &b)
{
int temp = a;
a = b;
b = temp;
}
void quickSort(int nums[], int left, int right)
{
if (left >= right)
return;
int jizhun=nums[left];
int i = left, j = right;
while (i <= j)
{
while (nums[j] > jizhun)
j--;
while (nums[i] <jizhun)
i++;
if (i <= j)
{
swap(nums[i], nums[j]);
i++;
j--;
}
}
quickSort(nums, left, j);
quickSort(nums, i, right);
}
int main()
{
int nums[10] = {3, 5, 2, 6, 8, 1, 0, 4, 7, 9};
quickSort(nums, 0, 9);
for (int i = 0 ; i < 10; i++)
{
cout << nums[i] << " ";
}
}
#include <iostream>
using namespace std;
void swap(int &a, int &b)
{
int temp = a;
a = b;
b = temp;
}
void quickSort(int nums[], int left, int right)
{
if (left >= right)
return;
int pivot = nums[left + (right - left) / 2];
int i = left, j = right;
while (i <= j)
{
while (nums[i] < pivot)
i++;
while (nums[j] > pivot)
j--;
if (i <= j)
{
swap(nums[i], nums[j]);
i++;
j--;
}
}
quickSort(nums, left, j);
quickSort(nums, i, right);
}
int main()
{
int nums[10] = {3, 5, 2, 6, 8, 1, 0, 4, 7, 9};
quickSort(nums, 0, 9);
for (int i = 0 ; i < 10; i++)
{
cout << nums[i] << " ";
}
}
4.3.2冒泡排序
//冒泡排序
#include<bits/stdc++.h>
using namespace std;
template <class T>
void BubbleSort(T A[], int n)
{
int i, j;
bool flag;
T temp;
for (i = n-1, flag = 1; i > 0 && flag; i--)//用flag控制是否继续比较
{
flag = false;//设置未交换标志
for (j = 0; j < i; j++)
{
if (A[j+1] < A[j])
{
flag = true;//有交换发生要修改置换标志
temp = A[j+1];
A[j+1] = A[j];
A[j] = temp;
}
}
}
}
4.4归并排序
#include<bits/stdc++.h>
using namespace std;
void TwoWayMerge(int Dst[],int Src[],int s,int e1,int e2)
{
//两个子文件归并为一个子文件
//原数组中[s:e1]与[e1+1:e2]归并到目的数组中[s:e2]
int s1,s2;
for(s1=s,s2=e1+1;s1<=e1 && s2<=e2;)//两段数据都是从头开始的
{
if(Src[s1]<=Src[s2])
{
Dst[s]=Src[s1];
s++;
s1++;
}
else
{
Dst[s]=Src[s2];
s++;
s2++;
}
}
if(s1<=e1)//左序列和右序列已经比较完了,此时右序列是空了,就把左序列剩下的放进去
{
memcpy(&Dst[s],&Src[s1],(e1-s1+1)*sizeof(int));
}
else
{
memcpy(&Dst[s],&Src[s2],(e2-s2+1)*sizeof(int));
}
}
void OnePassMerge(int Dst[],int Src[],int len,int n)
{
//一趟归并:每两个相邻子文件归并,子文件长度为len
int i;
for(i=0;i+2*len<n;i=i+2*len)//从第一组开始 两组两组合并 所以是2*len ,最后一对之前,因为到最后时i+2*len=n了
{
TwoWayMerge(Dst,Src,i,i+len-1,i+2*len-1);
}
if(i<n-len)//最后剩下的是大于一个组的,所以还得执行二并一
{
TwoWayMerge(Dst,Src,i,i+len-1,n-1);
}
else//只剩下了一组,那么不用排,直接把剩下的复制
{
memcpy(&Dst[i],&Src[i],(n-1)*sizeof(int));
}
}
//归并排序
void MergeSort(int A[],int n)
{
int k=1;//初始子文件的长度
int *B=new int(n);
while(k<n)
{
OnePassMerge(B,A,k,n);
k<<=1;//移位,相当于k*2
if(k>=n)
{
memcpy(A,B,n*sizeof(int));
}
else
{
OnePassMerge(A,B,k,n);
k<<=1;
}
}
delete B;
}
int main()
{
int a[10]={0,45,723,23,3,45,5,8,9,12345};
MergeSort(a, 10);
for(int i=0; i<10; i++)
cout<<a[i]<<" ";
return 0;
}
4.5基数排序
#include<bits/stdc++.h>
using namespace std;
const int MAXSIZE = 10000;
template<class T>//
class cQueue
{ int m_head, m_tail, m_maxSize;
T *m_a;//
public:
cQueue();
~cQueue();
bool push(const T& x);//
T front();//
void pop();
bool isEmpty();
bool isFull();
int size();
void clear();
};
template<class T>
cQueue<T>::cQueue()
{ m_a = new T[MAXSIZE];
m_maxSize = MAXSIZE;
m_head = m_tail = 0;
}
template<class T>
cQueue<T>::~cQueue()
{ delete m_a;
}
template<class T>
bool cQueue<T>::push(const T& x)
{ if(isFull()) return 0;
m_a[m_tail++] = x;
return true;
}
template<class T>
T cQueue<T>::front()
{ //if(m_head == m_tail) return NULL;//???
return m_a[m_head];
}
template<class T>
void cQueue<T>::pop()
{ if(m_head < m_tail) m_head++;
}
template<class T>
bool cQueue<T>::isEmpty()
{ return (m_head == m_tail) ? true : false;
}
template<class T>
bool cQueue<T>::isFull()
{ return (m_tail == m_maxSize) ? true : false;
}
template<class T>
int cQueue<T>::size()
{ return m_tail - m_head;
}
template<class T>
void cQueue<T>::clear()
{ m_head = m_tail = 0;
}
//基数排序:从小到大
template <class T>
void rSort(T a[],int n)
{
cQueue<T> que[10];//建0-9这样的十个队列
//确定回合数R--根据最大的那个数
int R=0;
T mx=a[0];
for(int i=1;i<n;i++)//找最大值mx
{
mx=max(a[i],mx);
}
while(mx)
{
R++;
mx/=10;
}
//基数排序
int d=1;
for(int i=1;i<=R;i++) //第1个回合到第R个回合
{
//将数据分配到10个队列中
for(int j=0;j<n;j++)
{
int t=a[j]/d%10;//
que[t].push(a[j]);
}
d *= 10;
//收集 10个队列里的数据
int p=0;
for(int j=0;j<10;j++)
{
while(que[j].size())
{
a[p++]=que[j].front();
que[j].pop();
}
}
}
}
int main()
{
int a[10]={0,45,723,23,3,45,5,8,9,12345};
rSort(a, 10);
for(int i=0; i<10; i++)
cout<<a[i]<<" ";
return 0;
}
第五章 查找
5.1结构
#include<bits/stdc++.h>
using namespace std;
struct tNode
{
int key;
};
tNode A[1000];
5.2顺序查找
将每个结点的关键字与给定的待查找的关键值进行比较,直到找到或者遍历完所有结点
//顺序查找
template<class T>
int SeqSearch( T A[],int n, char key)
{
for(int i=0;i<n;i++)
{
if(A[i].key==key)
{
return i;//成功 返回下标
}
}
return -1;
}
5.3折半查找(要求有序)
排序->找到中间结点->将其值与给定关键值比较,相等则成功->若当前值大于关键值,在前半部分寻找->否则在后半部分寻找
//先实现排序--快排
//快速排序
void QSort(int A[],int low,int high)//low最左,high最右
{
int i,j;
if(low>=high)
{
return;
}
i=low;
j=high;
int temp=A[i];//把A[i]变空位,A[i]保存进了temp
while(i<j)
{
while(i<j && A[j]>temp) //j必须小于temp 才会放至左半边,不满足时继续往前找
{
j--;
}
if(i<j)//满足A[j]<temp时
{
A[i]=A[j];//就把 A[j]放入A[i];
i++;
}
while(i<j && A[i]<=temp)
{
i++;
}
if(i<j)
{
A[j]=A[i];
j--;
}
}
A[i]=temp;
QSort(A,low,j-1);
QSort(A,i+1,high);
}
template<class T>
int BinarySearch(T A[],int n,int key)
{
int low,high,mid;//位置下标
//初始查找区间为整个表
low=0;
high=n-1;
QSort(A,low,high);
while(low<=high)
{
//计算中间结点的位置
mid= (low+high)/2;
if(key==A[mid].key)
{
return mid;
}
else if(key>A[mid].key)
{
//继续查找后半部分
low=mid+1;
}
else
{
//继续查找前半部分
high=mid-1;
}
}
}
5.4分块查找
#include <stdio.h>
#include <iostream>
#include <stdlib.h>
using namespace std;
//索引表
typedef struct //把struc结构体t定义为一种类型,可以用它再继续定义其他的
{
int key;//这个索引块中最大关键字的值
int start,end;//索引表中第一个元素的下标和块结束的下标
}Node;//索引块结构
//多个索引块构成一个索引表
typedef struct
{
Node idx[10];//表项
int len;//表长
}IdxTable;//索引表结构
//对于块来说,每一块中关键字最大的元素是要小于下一块中关键字最小的元素
//分块查找
IdxTable table;// table就是索引表
int BlockingSearch(int key,int a[])
{
//折半查找遍历索引表
int low,high,mid;
low=1;//因为high是从len 就是长度,所以low是从1开始的
high=table.len;
while(low<=high)
{
mid=(low+high)/2;
if(key<=table.idx[mid].key)//要找的key 小于了索引块的关键字
{
//顺序查找
if(key<=table.idx[mid-1].key)//为什么还要判断mid-1?
{
high=mid-1;
}
else
{
for(int i=table.idx[mid].start;i<table.idx[mid].end;i++)
{
if(key==a[i])
{
return (i+1);
}
}
return 0;
}
}
else
{
low=mid+1;
}
}
return 0;
}
int main()
{
int i;//key的下标
int a[] = {22,12,13,8,9,20,33,42,44,38,24,48,60,58,74,49,86,53 };
//索引表
table.idx[1].key = 22; table.idx[1].start = 0; table.idx[1].end = 5; // 22 0 5
table.idx[2].key = 48; table.idx[2].start = 6; table.idx[2].end = 11; // 48 6 11
table.idx[3].key = 86; table.idx[3].start = 12; table.idx[3].end = 17; // 86 12 17
table.len = 3;
int key;
cin>>key;
i=BlockingSearch(key,a);
cout<<i<<" ";
return 0;
}
5.5 KMP!!!
#include<bits/stdc++.h>
using namespace std;
bool compare(char *q,char *p,int len) //比较前后缀是否相同
{
for (int i = 0; i < len; i++)
{
if (q[i] != p[i])
return false;
}
return true;
}
void getNext(char* p, int next[])
{
next[0] = -1; //next数组里面储存的是 下一次子串的比较指针应该指向的位置;
next[1] = 0;
for (int i = 2; i < strlen(p); i++)
{
for (int j = i-1 ; j >= 0; )
{
if (j == 0)
{
next[i] = 0;
break;
}
if (compare(p, p + i- j, j))//比较前后缀
{
next[i] = j;
break;
}
else
j--;
}
}
for (int i = 1; i < strlen(p); i++)
{
if (p[i]==p[next[i]])
{
next[i] = next[next[i]];
}
}
}
int main()
{
int next[1000];
char T[1000], P[1000];
cin >> T >> P;
getNext(P, next);
int i, j;
for (i = 0, j = 0; i < strlen(P) && j < strlen(T);)
{
if (P[i] == T[j])
{
i++;
j++;
continue;
}
if (next[i] >= 0)
{
i = next[i];
}
else
{
i = 0;
j++;
}
}
if (i>=strlen(P))
{
cout << j - strlen(P) << endl;
}
else
cout << "don`t exist";
}
BF(朴素查找算法)算法
int brute_force_search(const char* text, const char* pattern)
{
int n = strlen(text);
int m = strlen(pattern);
for (int i = 0; i <= n - m; ++i) {
int j;
for (j = 0; j < m; ++j) {
if (text[i + j] != pattern[j]) {
break;
}
}
if (j == m) { // 找到匹配位置
return i;
}
}
return -1; // 没有找到
}
第六章 树
6.1树的概念
6.1.1基本术语
度数:结点的子树的个数
树叶:没有子树的结点
分支节点:非终端结点
子孙:根为r的树中所有的结点都是r的子孙,除r外的叫做r的真子孙
祖先:从根r到结点p的路径(有且仅有一条这样的路径)上的所有结点都是p的祖先,除p外都是真祖先
层数:树根的层数为1,其他节点的层数为其父节点的层数+1
高度:结点的最大层数
树林:n个互不相交的树的集合
6.2二叉树
6.2.1二叉树的概念
每个结点至多有两个儿子,且有左右之分。
深度:二叉树的高度;只有一个根节点的话是1
6.2.2二叉树的性质
6.1任何一颗含有n个结点的二叉树恰有n-1条边
证明:除根结点外的其他结点都只有一条边于父节点相连
6.2深度为h的二叉树,至多有2h-1个结点
证明:第一层至多有21-1个……
6.3满二叉树:深度为h且有2h-1个结点的二叉树
*6.4完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
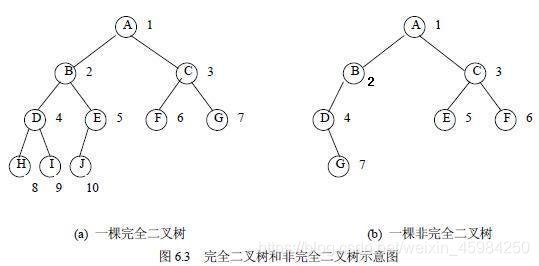
判断方法:
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
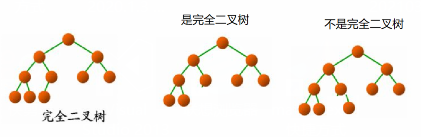
6.4完全二叉树的性质:若 对一棵有n个结点的完全二叉树的结点,按层次次序编号(每层从左至右),对任意一节点:
1).若i=1,则为根节点,若i>1,则结点i/2为其父节点
2).若2i>n,则结点i无左二子,否则2i为结点i的左二子
3).若2i+1>n,则结点i无右儿子,否则2i+1为其右儿子
6.5如果一棵二叉树每个分支节点都有两个儿子,设叶节点个数为n,则分支节点个数为n-1
证明:设分支节点个数为x,那么就有2x条边,结点总数为x+n;边为节点数-1;所以2x=x+n-1;所以x=n-1
6.2.3输入一棵二叉树,输出父节点
#include<bits/stdc++.h>
using namespace std;
输入一个二叉树 输出父节点
int main()
{
int n;
cin>>n;
char t[1000];
for(int i=1;i<=n;i++)
{
cin>>t[i];
}
char key;
cin>>key;
for(int i=1;i<=n;i++)
{
if(t[i]==key)
{
cout<< t[i/2] <<endl;
}
}
return 0;
}
6.2.4链接存储构建二叉树
//输入一颗二叉树,采取链式存储,输出该树最左边的全部结点的值
//输入: 节点数
//节点编号 数据 左孩子编号 右孩子编号
template<class T>
struct tNode
{
T data;//数据
int num;//编号
tNode *pL,*pR;//左右孩子指针
};
const int MAXSIZE=20000;
tNode<char> tree[MAXSIZE];
int main()
{
int N;
cin>>N;
int a,L,R;//L,R表示结点的编号
char d;//数据
for(int i=1;i<=N;i++)
{
cin>>a>>d>>L>>R;
tree[a].data=d;
tree[a].num=a;
if(!L)
{
tree[a].pL=NULL;
}
else
{
tree[a].pL=&tree[L];
}
if(!R)
{
tree[a].pR=NULL;
}
else
{
tree[a].pR=&tree[R];
}
}
//搜索
tNode<char> *p=&tree[1];
while(p)
{
cout<<p->data<<" ";
p=p->pL;
}
return 1;
}
/*
输入
8
1 A 2 3
2 B 0 4
3 C 5 6
4 E 7 8
5 F 0 0
6 G 0 0
7 H 0 0
8 I 0 0
*/
6.2.4树与二叉树的相互转化(孩子兄弟表示法)
结点:
1.结点的值
2.指向第一个孩子结点的指针
3.指向兄弟结点的指针
将树转换成二叉树的步骤是:
(1)加线。就是在所有兄弟结点之间加一条连线;
(2)抹线。就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;
(3)旋转。就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
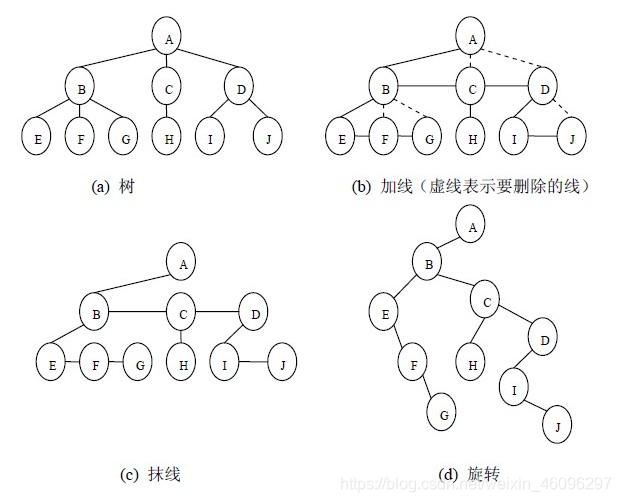
6.3二叉树的遍历
前序:先根后左后右
中序:先左后根后右
后序:先左后右后根
6.3.1非递归遍历
#include<bits/stdc++.h>
using namespace std;
/*
输入一棵二叉树,采用链接存储,非递归前序、中序、后续遍历二叉树。
【输入格式】
节点数
节点的编号 结点的值 左孩子编号 右孩子编号
//0表示没有孩子
【输出格式】
中序序列,中间用空格隔开
*/
template <class T>
struct tNode
{
int id;//结点编号
T data;//结点值
tNode *pL,*pR;
};
const int MAXSIZE=20000;
tNode<char> tree[MAXSIZE];//这棵树
int N;//结点的总个数
template <class T>
void preOrder(tNode<T> *p)//非递归前序遍历,p指向根节点
{
tNode<T> *st[1000];//动态的那个栈
int top=0;//
st[0]=p;//先把根节点压入
while(st[top] || top>0)//栈顶不为空,或者栈顶为空但top>0
{
if(st[top]!=NULL)//当栈顶元素不空
{
cout<<st[top]->data<<" ";//把值输出
st[top+1]=st[top]->pL ;//再把它的左孩子压入
top++;
}
else//栈顶此时为空
{
top--;//那就把栈顶弹出
st[top]=st[top]->pR;//用此时栈顶的右孩子取代栈顶
}
}
}
template<class T>
void inOrder(tNode<T> *p)
//非递归中序遍历。p指向根节点 --?
{
tNode<T> *st[1000];
int top=0;
st[0]=p;
do//先执行一遍循环代码再开始判断循环条件
{
while(st[top]!=NULL)
{
st[top+1]=st[top]->pL;
top++;
}
if(top>0)
{
cout<<st[--top]->data<<" ";
st[top]=st[top]->pR;
}
}while(top>0 ||st[top]!=NULL);
}
template<class T>
void postOrder(tNode<T> *p)
//非递归后序遍历。p指向根节点
{
tNode<T> *st[1000];
int tag[1000];//技巧:用tag[i]来记录st[i] 位置的结点的左右子树是否已被遍历;
//0表示左子树已被遍历,1表示左右子树均已遍历
int top=0;
st[0]=p;
tag[0]=0;
do
{
//将左边节点一次压进栈,最后压入NULL;
while(st[top])
{
st[top+1]=st[top]->pL;
tag[++top]=0;
}
while(tag[top-1]==1)
{
cout<<st[--top]->data<<" ";
}
//栈顶替换为次栈顶的右孩子
if(top>0)
{
st[top]=st[top-1]->pR;
tag[top-1]=1;
tag[top]=0;
}
}while(top!=0); //栈=0是结束标志
}
int main()
{
int id,L,R;
char d;
//构建二叉树
cin>>N;
for(int i=0;i<N;i++)
{
cin>>id>>d>>L>>R;
tree[id].data=d;
if(!L)
{
tree[id].pL=NULL;
}
else
{
tree[id].pL=&tree[L];
}
if(!R)
{
tree[id].pR = NULL;
}
else
{
tree[id].pR = &tree[R];
}
}
cout<<"前序序列:";
preOrder(&tree[1]); cout<<endl;
cout<<"中序序列:";
inOrder(&tree[1]); cout<<endl;
cout<<"后序序列:";
postOrder(&tree[1]);
return 0;
}
/*
输入样例1:
9
1 A 2 3
2 B 4 5
3 H 6 0
4 C 7 8
5 F 9 0
6 I 0 0
7 D 0 0
8 E 0 0
9 G 0 0
输出样例1;
前序序列:A B C D E F G H I
中序序列:D C E B G F A I H
后序序列:D E C G F B I H A
*/
6.3.2中序线索化二叉树
#include<bits/stdc++.h>
using namespace std;
/*
中序线索化二叉树。输出中序遍历序列。
【输入格式】
节点数
节点的编号 左孩子编号 右孩子编号(0表示没有孩子)
【输出格式】
中序遍历序列
*/
template<class T>
struct tNode
{
T data;
tNode *L,*R;
bool lTag, rTag;
};
const int MAXSIZE = 20000;
tNode<int> tree[MAXSIZE];
int N;
#define HasNoLeftSon(p) ((p)->lTag==1)//没有左孩子
#define HasLeftSon(p) ((p)->lTag==0)//有左孩子
#define HasNoRightSon(p) ((p)->rTag==1)//没有右孩子
#define HasRightSon(p) ((p)->rTag==0)//有右孩子
template<class T>
tNode<T>* BT_Threadize(tNode<T>* root, tNode<T>* pre)
//对以root为根的子树进行中序线索化。pre为以root为根
//的子树的中序首结点的中序前驱指针,返回以root为根的
//子树的中序尾结点指针
{
if (root==NULL)
return pre;
if (root->L) //对左子树来说pre始终是前驱
{
tNode<T>* last=BT_Threadize(root->L, pre);
last->R=root; //尾结点last的后继是根结点
}
else
{
root->L=pre;
root->lTag=1;
}
if (root->R)
return BT_Threadize(root->R, root);
else
{
root->rTag=1;
return root; //root为子树的尾节点
}
}
template<class T>
tNode<T>* BT_GetMidPrev(tNode<T>* p)
//获取中序线索化二叉树中结点p的中序前驱
{ //p没有左孩子:线索指向前驱
if( HasNoLeftSon(p))
return p->left;
//p有左孩子:前驱为左孩子的右子树的最右结点
tNode<T>* curr=p->left;//goto left son
while( HasRightSon(curr) ) //while curr has right son
curr=curr->right; //goto right son
return curr;
}
template<class T>
tNode<T>* BT_GetMidNext(tNode<T>* p)
//获取中序线索化二叉树中结点p的中序后继
{
if( HasNoRightSon(p) )
return p->R;
//goto right son:后继为右孩子的左子树的最左结点
tNode<T>* curr= p->R;
//here, curr is not NULL
while( HasLeftSon(curr) )
curr=curr->L; //goto left son
return curr;
}
template<class T>
void BT_TraRootMid(tNode<T>* root)
//中序线索化二叉树的中序遍历非递归算法
{
if (root==NULL) return;
//找中序首结点cur
tNode<T>* curr=root;
while( HasLeftSon(curr) ) curr=curr->L;
while (curr)//遍历后继结点
{
cout<<curr->data<<" ";
curr=BT_GetMidNext(curr);
}
}
int main()
{
int a, L, R;
//构建二叉树
cin>>N;
for(int i=0; i<N; i++)
{
cin>>a>>L>>R;
tree[a].data = a;
if(!L)
tree[a].L = NULL;
else
tree[a].L = &tree[L];
if(!R)
tree[a].R = NULL;
else
tree[a].R = &tree[R];
}
//中序线索化
tNode<int> *pre=NULL;
BT_Threadize(&tree[1], pre);
//中序遍历
BT_TraRootMid(&tree[1]);
return 0;
}
/*
输入样例1:
8
1 2 0
2 4 5
3 7 0
4 0 6
5 0 3
6 8 0
7 0 0
8 0 0
输出样例1;
4 8 6 2 5 7 3 1
*/
第七章 树形结构的应用
7.1二叉排序树
二叉树中的任何结点的左子树中的所有节点的关键字值都小于该节点的关键字值,右子树中所有节点的关键字值都大于该节点的关键字值
7.1.1二叉排序树的构建
7.1.2最佳二叉排序树(等概率)
扩充二叉树
对于一棵二叉树的结点,若出现空的子树,就增加一个对应的空叶节点,新增加的叶节点称为外部结点,原有结点称为内部节点
有n个内部节点时,有n+1个外部结点
也就是完全二叉树形式的二叉排序树
内外部路径长度
构建最佳二叉排序树
1.首先要将关键字排序(直接用sort函数)
2.折半查找法依次查找中间结点下标,第一次找到的作为根节点插入
后面用递归算法依次插入
#include<bits/stdc++.h>
using namespace std;
template<class T>
class node
{
public:
T data;
node*Rnode;
node*Lnode;
};
//后序遍历
void BackOrder(node<int>* t)
{
if(!t)
return;
BackOrder(t->Lnode);
BackOrder(t->Rnode);
cout<<(t->data)<<" ";
}
//前序遍历
void FrontOrder(node<int>* t)
{
if(!t)
return;
cout<<(t->data)<<" ";
FrontOrder(t->Lnode);
FrontOrder(t->Rnode);
}
//中序遍历
void InOrder(node<int>* t)
{
if(!t)
return;
InOrder(t->Lnode);
cout<<(t->data)<<" ";
InOrder(t->Rnode);
}
template<class T>
void createTree(node<T>* &r,T A[],int s,int e)
{
if (s>e)
return ;
int t = (s+e)/2;
r=new node<T>;
r->Lnode=r->Rnode=NULL;
r->data=A[t];
createTree(r->Lnode,A,s,t-1);
createTree(r->Rnode,A,t+1,e);
}
int main()
{
int n;
cin>>n;
int A[100];
for (int i =0; i<n; i++)
{
cin>>A[i];
}
sort(A,A+n);
node<int>* r=NULL ;
createTree(r,A,0,n-1);
cout<<"前序输出:";
FrontOrder(r);
cout<<endl;
cout<<"中序输出:";
InOrder(r);
}
/*测试用例
输入样例:
9
7 4 2 6 17 11 8 13 9
输出样例:
前序:8 4 2 6 7 11 9 13 17
中序:2 4 6 7 8 9 11 13 17
输入样例: //类型是string类型
8
abc efg zab cab cad efy rab xyz;
输出样例:
前序:efg cab abc cad rab efy xyz zab
中序:abc cab cad efg efy rab xyz zab
*/
7.1.3二叉排序树的查找、插入、删除结点
查找
从根节点起,沿左子树或者右子树向下搜索,当x<根节点的值,则沿着左子树下降搜索;当x>根节点的值,则沿着右子树下降搜索
template<class T>
tNode<T> *GetNode(tNode<T> *root,T x)
{
tNode<T> *cur=root;
while(cur && cur->data!=x)
{
if(x<cur->data)
{
cur=cur->pL;
}
else
{
cur=cur->pR;
}
}
return cur;
}
插入
如果是空树,则插入的结点作为根节点;如果不是空树,则插入的结点就与根节点比较,然后小于就往左走,如果左子树不存在,那么就把他放在左子树的位置;若存在,那就继续往左找;大于往右走;如果右子树不存在,那么就把他放在右子树的位置;若存在,那就继续往左找;
//在二叉排序树中插入结点
template<class T>
void insert(tNode<T>* root,T x)
{
tNode<T>*tmp=new tNode<T>;
tmp->data=x;
tmp->pL=tmp->pR=NULL;
while(root)//根节点存在
{
if(x<root->data)
{
if(!root->pL)
{
root->pL=tmp;
return;
}
else
{
root=root->pL;
}
}
else
{
if (!root->pR)
{
root->pR = tmp;
return;
}
else
root = root->pR;
}
}
}
删除t
分三种情况:
1.删除的结点为叶节点:直接判断是fa的左孩子还是右孩子然后删掉;
2.删除的结点有一个孩子:先判断t的孩子是左孩子还是右孩子;然后判断待t是fa的左节点还是右节点
//待删除的结点有一个孩子
if((t->pL!=NULL && t->pR==NULL )|| (t->pL==NULL && t->pR!=NULL))
{
if(t->pL!=NULL)//t只有左孩子
{
if(fa->pL==t)
{
fa->pL=t->pL;
}
if(fa->pR==t)
{
fa->pR=t->pL;
}
delete t;
}
else//t只有右孩子
{
if(fa->pL==t)
{
fa->pL=t->pR;
}
if(fa->pR==t)
{
fa->pR=t->pR;
}
delete t;
}
}
//待删除的结点有两个孩子
else
{
//找到t的左子树的最右边的结点Q-这是左子树的最大值(因为是二叉排序树)
//代替t,删除t,删除Q
tNode<T> *Q=t->pL;//从t的左孩子开始找
while(Q->pR)//一路向右
{
Q=Q->pR;
}
T temp=Q->data;//先保存Q
//因为要考虑Q是否有左子树,不能简单删除
//递归删除Q
DelNode(root,Q->data);
t->data=temp;//把原来t改成Q;
delete Q;
}
return root;
}
完整代码(包括遍历)
//在二叉排序树中删除根节点
#include<bits/stdc++.h>
using namespace std;
//结点类
template <class T>
class tNode
{
public:
T data;//结点的值
tNode *pL, *pR; //左右孩子指针
};
tNode<int> *root;
int N;
//在二叉排序树中插入结点
template<class T>
void insert(tNode<T>* root,T x)
{
tNode<T>*tmp=new tNode<T>;
tmp->data=x;
tmp->pL=tmp->pR=NULL;
while(root)//根节点存在
{
if(x<root->data)
{
if(!root->pL)
{
root->pL=tmp;
return;
}
else
{
root=root->pL;
}
}
else
{
if (!root->pR)
{
root->pR = tmp;
return;
}
else
root = root->pR;
}
}
}
//找到要删除的结点
template<class T>
tNode<T> *GetNode(tNode<T> *root,T x)
{
tNode<T> *cur=root;
while(cur && cur->data!=x)
{
if(x<cur->data)
{
cur=cur->pL;
}
else
{
cur=cur->pR;
}
}
return cur;
}
//找到某个结点的父节点
template<class T>
tNode<T> *GetFa(tNode<T> *root, tNode<T> *t)//注意 tNode<T> *t
{
tNode<T> *cur=root;
while(cur)
{
if(cur->pL==t ||cur->pR==t)
{
return cur;
}
else
{
if(t->data<cur->data)
{
cur=cur->pL;
}
else
{
cur=cur->pR;
}
}
}
return cur;
}
//删除某个结点
template<class T>
tNode<T>* DelNode(tNode<T> *root,T x)
{
tNode<T> *t=GetNode(root,x);
tNode<T> *fa=GetFa(root,t);//注意这是t
//待删除的为叶节点
if(t->pL==NULL && t->pR==NULL)
{
//判断待删结点是fa的左还是右孩子然后删掉
if(fa->pL==t)
{
fa->pL=NULL;
}
else
{
fa->pR=NULL;
}
//注意!!先改结点再删!!
delete t;
}
//待删除的结点有一个孩子
if((t->pL!=NULL && t->pR==NULL )|| (t->pL==NULL && t->pR!=NULL))
{
if(t->pL!=NULL)//t只有左孩子
{
if(fa->pL==t)
{
fa->pL=t->pL;
}
if(fa->pR==t)
{
fa->pR=t->pL;
}
delete t;
}
else//t只有右孩子
{
if(fa->pL==t)
{
fa->pL=t->pR;
}
if(fa->pR==t)
{
fa->pR=t->pR;
}
delete t;
}
}
//待删除的结点有两个孩子
else
{
//找到t的左子树的最右边的结点Q-这是左子树的最大值(因为是二叉排序树)
//代替t,删除t,删除Q
tNode<T> *Q=t->pL;//从t的左孩子开始找
while(Q->pR)//一路向右
{
Q=Q->pR;
}
T temp=Q->data;//先保存Q
//因为要考虑Q是否有左子树,不能简单删除
//递归删除Q
DelNode(root,Q->data);
t->data=temp;//把原来t改成Q;
delete Q;
}
return root;
}
//前序遍历函数
template <class T>
void preOrder(tNode<T> *t)//从根节点开始
{
if(!t)
return;
cout << t->data << " ";
//递归左右子树
preOrder(t->pL);
preOrder(t->pR);
}
//中序遍历函数
template <class T>
void inOrder(tNode<T> *t)//从根节点开始
{
if(!t)
return;
inOrder(t->pL);
cout << t->data << " ";
inOrder(t->pR);
}
int main()
{
int d;//数据
cin>>N;
int del[4];//待删数据
//构建根节点
cin>>d;
root=new tNode<int>;
root->data=d;
root->pL=root->pR=NULL;
//构建二叉树的其他部分,依次插入
for(int i=1;i<N;i++)
{
cin>>d;//输入数据
insert(root,d);
}
for(int j=0;j<4;j++)
{
cin>>del[j];
}
for(int k=0;k<4;k++)
{
DelNode(root,del[k]);
cout<<"前序:";
preOrder(root);
cout<<endl;
cout << "中序:";
inOrder(root);
cout << endl;
cout << "=================" << endl;
}
return 0;
}
/*
输入样例
9
7 4 2 6 17 11 13 8 9
4 6 11 13
输出样例
前序:7 2 6 17 11 8 9 13
中序:2 6 7 8 9 11 13 17
=================
前序:7 2 17 11 8 9 13
中序:2 7 8 9 11 13 17
=================
前序:7 2 17 9 8 13
中序:2 7 8 9 13 17
=================
前序:7 2 17 9 8
中序:2 7 8 9 17
=================
*/
7.2 Huffman最优二叉树
需要一个权值的数组w[ ]; --首先将权值结点初始化为叶节点–生成n-1个非叶结点ht[n+1…2*n-1] (最小的两棵合成一棵新的,新树的左右结点分别指向刚找到的那两棵小的)–在ht[1…k-1]中找权值最小的两棵树first, second–找到之后,创建其父节点–之后再前序+中序遍历
#include<bits/stdc++.h>
using namespace std;
template <class T>
struct node
{
T data;//叶节点的符号
int weight;//叶节点的权值
int father;//父节点编号,-1表示无父节点
int left;// 左儿子结点编号,-1表示无左儿子
int right; //右儿子结点编号,-1表示无右儿子
};
const int MAXSIZE = 20000;
const int INF = 1000000;//表示无穷大
int N;//结点的个数
int W[MAXSIZE/2];//储存权值的数组
node<char> ht[MAXSIZE]; //这棵Huffman树,根节点是ht[2*N-1]
int path[MAXSIZE/2];//记录叶节点的路径
//由n个权值w[0..n-1]生成Huffman树,存储在ht[]中
void creatHfm(int *w,int n)
{
//首先将权值结点初始化为叶节点
for(int k=1; k<=n; k++) //注意是从k=1开始
{
ht[k].weight=w[k-1];
ht[k].father=-1;
ht[k].left=-1;
ht[k].right=-1;
}
//生成n-1个非叶结点ht[n+1..2*n-1] (最小的两棵合成一棵新的,新树的左右结点分别指向刚找到的那两棵小的)
for(int k=n+1; k<=2*n-1; k++) //合成的那棵树先放到n+1的位置所以k=n+1
{
//先在ht[1..k-1]中找权值最小的两棵树first, second
int first=k,second=k;
ht[k].weight=INF;
for(int i=1; i<k; i++)
{
if(ht[i].father <0 && ht[i].weight<ht[first].weight)
{
second=first;
first=i;
}
else if(ht[i].father <0 && ht[i].weight<ht[second].weight)
{
second=i;
}
}
//找到之后,创建其父节点
ht[k].weight=ht[first].weight+ht[second].weight;
ht[k].left=first;//指向的那个位置!!!
ht[k].right=second;
ht[k].father=-1;
ht[first].father=k;//注意!father,first,second都是下标
ht[second].father=k;
}
}
void preOrder(int p)
{
if(p==-1)
{
return ;
}
if(ht[p].data)
{
cout<<ht[p].data<<" ";
}
else
{
cout<<"X";//非叶节点
}
preOrder(ht[p].left);
preOrder(ht[p].right);
}
void inOrder(int p)
{
if(-1 == p)
return;
inOrder(ht[p].left);
if(ht[p].data)
cout<<ht[p].data<<" ";
else
cout<<"X ";//非叶节点
inOrder(ht[p].right);
}
void prt(int d, char c)
{
cout<<c<<": ";
for(int i=0; i<d; i++)
cout<<path[i];
cout<<endl;
}
void dfs(int p, int d)
{
if(-1 == ht[p].left && -1 == ht[p].right)//搜索完一条路径
{
prt(d, ht[p].data);
return;
}
if(-1 != ht[p].left)
{
path[d] = 0;
dfs(ht[p].left, d+1);
}
if(-1 != ht[p].right)
{
path[d] = 1;
dfs(ht[p].right, d+1);
7.3堆排序
实质上是一棵完全二叉树的层次序列
插入:先把待插入的结点放在最后一个位置,然后进行上浮操作,也就是和父节点比(index/2),大于父节点就swap
删除:只删除根节点–先向下找到最后一个位置,然后如果比那个位置的元素小,那就交换,此时index在最上面,然后进行下沉操作
#include <iostream>
#include <vector>
using namespace std;
class Heap//堆
{
public:
Heap();//构造函数
void insert(int val);//插入一个值为val的结点
int remove();//删除堆顶点并返回其值
private:
vector<int> data;//存储堆结点的数组
void Up(int index);//上浮函数
void Down(int index);//下沉函数
};
Heap::Heap()
{
data.push_back(-1);//为了方便计算,data的第一个元素为-1
}
void Heap::insert(int val)
{
data.push_back(val);
Up(data.size()-1);
}
int Heap::remove()
{
if(data.size()<=1)
{
return -1;//堆为空
}
int ret=data[1];//根节点
data[1]=data.back() ;//back函数是找到数组中的最后一个元素
data.pop_back();//把尾元素删除
Down(1) ;//1位置
return ret;
}
void Heap::Up(int index)//indxs是数组中的位置下标
{
while(index >1 && data[index]>data[index/2])
{
swap(data[index],data[index/2]);
index=index/2;
}
}
void Heap::Down(int index)
{
while(index*2 < data.size())//它的孩子结点仍然小于size,表示不是最后那个,可以下沉
{
int child=index*2;
//一路向下找到最后一个孩子
if(child+1<data.size() && data[child+1]<data[child])
{
child++;
}
if(data[index]<data[child])
{
swap(data[index],data[child]);
index=child;
}
else
{
break;
}
}
}
int main()
{
Heap h;
h.insert(3);
h.insert(1);
h.insert(6);
h.insert(5);
h.insert(2);
h.insert(4);
while(true)//不断的删除元素并输出,直到堆为空;
{
int val=h.remove();//删除堆顶元素并将其值存储在变量 val 中
if(val==-1)
{
break;
}
cout<<val<<" ";
}
return 0;
}
第八章 图
8.1基本概念
8.2图的存储表示
8.2.1相邻矩阵表示图
8.2.2图的多重邻接表表示
#include<bits/stdc++.h>
using namespace std;
template<class T>
struct tVertex //顶点表
{
T data;
int firstEdge;
};
template<class T>
struct tEdge //边表
bool b; //访问标记
T i; //边的起点
int iLink; //i关联的下一条边的编号
T j; //边的终点
int jLink; //i关联的下一条边的编号
};
const int MAXSIZE = 200;
int N, M; //顶点数量、边的数量
tVertex<char> V[MAXSIZE]; //顶点表
tEdge<char> E[MAXSIZE]; //边表
int C=0; //边表中当前的边数量
//获取顶点x在顶点表中的编号(即下标),0表示不存在。
int vertexID(char x)
{
for(int i=1; i<=N; i++)
if(V[i].data == x) return i;
return 0;
}
//输出边表
void prt()
{
for(int i=1; i<=M; i++)
cout<<E[i].i<<" "<<E[i].iLink<<" "<<E[i].j<<" "<<E[i].jLink<<endl;
}
//在边表pos位置放入一条边(u,v)
void insertEdge(char u, char v, int pos)
{
//在边表位置pos放入一条边(u,v)
E[pos].i = u;
E[pos].j = v;
E[pos].iLink = 0;
E[pos].jLink = 0;
//修改边表
int k;
k = V[vertexID(u)].firstEdge; // k:u关联的第一条边在边表中的位置
//搜索此前u关联的最后一条边k,并指向pos
if(k != pos) //k=pos表明(u,v)是顶点u的第一条边
{
while(1)
{
if(E[k].i==u && E[k].iLink)
k = E[k].iLink;
else if(E[k].j==u && E[k].jLink)
k = E[k].jLink;
if(E[k].i==u && !E[k].iLink)
{
E[k].iLink = pos;
break;
}
if(E[k].j==u && !E[k].jLink)
{
E[k].jLink = pos;
break;
}
}
}
k = V[vertexID(v)].firstEdge; // k:v关联的第一条边在边表中的位置
//搜索此前v关联的最后一条边k,并指向pos
if(k != pos) //k=pos表明(u,v)是顶点v的第一条边
{
while(1)
{
if(E[k].i==v && E[k].iLink) k = E[k].iLink;
else if(E[k].j==v && E[k].jLink) k = E[k].jLink;
if(E[k].i==v && !E[k].iLink)
{
E[k].iLink = pos;
break;
}
if(E[k].j==v && !E[k].jLink)
{
E[k].jLink = pos;
break;
}
}
}
//prt();
}
int main()
{
int id; //顶点在顶点表中的位置
cin>>N;
for(int i=1; i<=N; i++)
{
cin>>V[i].data;
V[i].firstEdge = 0; //0:表示没有边
}
char x, y;
cin>>M;
for(int i=0; i<M; i++)
{
cin>>x>>y;
C++; //增加一条边,C也是边(x,y)在边表中的位置
//修改顶点表V
id = vertexID(x);
if(!V[id].firstEdge) V[id].firstEdge = C; //u首次出现
id = vertexID(y);
if(!V[id].firstEdge) V[id].firstEdge = C; //v首次出现
insertEdge(x, y, C); //(x,y)放入边表C位置
}
cout<<endl;
for(int i=1; i<=N; i++)
cout<<V[i].data<<" "<<V[i].firstEdge<<endl;
cout<<endl;
prt(); //输出边表
return 0;
}
/*
【输入样例1】
5
A B C D E
6
A B
A C
C B
D B
D C
C E
【输出样例1】
A 1
B 1
C 2
D 4
E 6
A 2 B 3
A 0 C 3
C 5 B 4
D 5 B 0
D 0 C 6
C 0 E 0
【输入样例2】
5
A B C D E
6
A B
A C
C B
D B
D C
E C
【输出样例2】同样的图,只是输入时边的端点不同
A 1
B 1
C 2
D 4
E 6
A 2 B 3
A 0 C 3
C 5 B 4
D 5 B 0
D 0 C 6
E 0 C 0
*/
8.3图的遍历
8.3.1宽度优先算法(BFS遍历)
(需要用到队列实现)图的宽度优先遍历(BFS)算法是一个分层搜索的过程,和树的层序遍历算法相同。在图中选中一个节点,作为起始节点,然后按照层次遍历的方式,一层一层地进行访问。
图的宽度优先遍历需要一个队列作为保存当前节点的子节点的数据结构。具体的算法如下所示:
(1) 顶点 V 入队列。
(2) 当队列非空时继续执行,否则算法为空。
(3) 出队列,获得队头节点 V,访问顶点 V 并标记 V 已经被访问。
(4) 查找顶点 V 的第一个邻接顶点 col。
(5) 若 V 的邻接顶点 col 未被访问过,则 col 进队列。
(6) 继续查找 V 的其他邻接顶点 col,转到步骤(5),若 V 的所有邻接顶点都已经被访问过,则转到步骤(2)。
#include<bits/stdc++.h>
#include<queue>
using namespace std;
const int MAXN = 100;
bool vis[MAXN] = {false}; // 标记每个节点是否被访问过
void bfs(int G[][MAXN], int n, int start)
{
queue<int> q;
q.push(start); // 将起始节点start加入队列
while(!q.empty())
{
int cur = q.front(); // 取出队头元素,即当前需要被访问的节点
q.pop();
if(vis[cur]) continue; // 如果节点已经被访问,则跳过本次循环
vis[cur] = true; // 标记该节点已经被访问
// 访问当前节点,并对其未访问的邻接顶点进行入队操作
cout << cur << " "; // 输出当前节点
for(int i = 0; i < n; i++)
{
if(!vis[i] && G[cur][i] != 0) // 当前节点cur到i有一条边且i未被访问
q.push(i);
}
}
}
// 示例使用:
int main()
{
int G[MAXN][MAXN] = {0};
int n, m, u, v;
cin >> n >> m; // 输入节点个数n和边数m
for(int i = 0; i < m; i++)
{
cin >> u >> v; // 输入一条边的两个节点u和v
G[u][v] = G[v][u] = 1; // 如果是无向图,则需要将G[v][u]也设为1
}
bfs(G, n, 0); // 从第0个节点开始进行宽度优先遍历
return 0;
}
8.3.2深度优先算法(DFS遍历)
访问规则:访问出发顶点,一路向下访问,直到不能再访问,返回上一层结点: 继续一路向下访问,直到不能再访问,返回上一层结点:……
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100;
bool vis[MAXN]; // 标记每个节点是否被访问过
void dfs(int G[][MAXN], int n, int cur)
{
vis[cur] = true; // 标记当前节点已经被访问
cout << cur << " "; // 输出当前节点
for(int i = 0; i < n; i++)
{
if(G[cur][i] != 0 && !vis[i]) // 当前节点cur到i有一条边且i未被访问
dfs(G, n, i);
}
}
// 示例使用:
int main()
{
int G[MAXN][MAXN] = {0};
int n, m, u, v;
cin >> n >> m; // 输入节点个数n和边数m
for(int i = 0; i < m; i++)
{
cin >> u >> v; // 输入一条边的两个节点u和v
G[u][v] = G[v][u] = 1; // 如果是无向图,则需要将G[v][u]也设为1
}
memset(vis, false, sizeof(vis)); //初始化所有节点都未被访问
dfs(G, n, 0); // 从第0个节点开始进行深度优先遍历
return 0;
}
8.4最小代价生成树
prim算法(普里姆)
从图中任意取出一个顶点,把他当作一棵树,然后从这棵树相接的边中选取一条最短(权值最小)的边,并将这条边及其所连接的顶点也并入这棵树中,此时得到一颗有两个顶点的树。然后在这棵树中相连的顶点中选取最短的边,并将图中的所有顶点并入树中为止,此时得到的树就是最小生成树。

kruskal算法(克鲁斯卡尔) (适用于边较少的稀疏图)
(1)将图中的所有边都去掉。(2)将边按权值从小到大的顺序添加到图中,保证添加的过程中不会形成环(3)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
#include<bits/stdc++.h>
using namespace std;
const int MAX_N=1000;
int n,m;//n为节点数;m为边数
struct Edge
{
int u,v,w;//起点,终点,权重
};
//定义一个边表
Edge edges[MAX_N];
int fa[MAX_N];
//判断两个结点是不是同一个树--判断当前元素x所在集合的根节点是不是x(如果是,相当于它之前没被并到其他集合中)
//如果不是,则递归的向上查找其根节点
int find(int x)
{
return fa[x]==x ? x:fa[x]=find(fa[x]);
}
//定义一个比较函数,用于给边表排序
bool cmp(const Edge& a,const Edge& b)
{
if(a.w !=b.w)
{
return a.w<b.w;
}
if(a.u != b.u)
{
return a.u<b.u;
}
return a.v<b.v;
}
void kruskal()
{
sort(edges,edges+m,cmp);
//让每个结点都成一棵独立的树
for(int i=1; i<=n; i++)
{
fa[i]=i;
}
//定义一个数组,存每次选中的边
vector<Edge> ret;
//遍历边
for(int i=0; i<m; i++)
{
int u=edges[i].u;
int v=edges[i].v;
int w=edges[i].w;
//判断是否是一棵树
//如果不属于同一棵树 --归并
if(find(u)!=find(v))
{
fa[find(u)]=find(v);
ret.push_back(edges[i]);//然后把这条边加入到集合
}
}
//输出最小生成树
for(int i=0; i<ret.size(); i++)
{
cout<<ret[i].u<<" "<<ret[i].v<<" "<<ret[i].w<<endl;
}
}
int main()
{
cin >> n >> m;
for (int i = 0; i < m; i++)
cin >> edges[i].u >> edges[i].v >> edges[i].w;
kruskal();
return 0;
}
/*
7 12
2 5 10
4 6 8
4 5 7
5 7 6
3 6 5
2 7 4
1 3 4
2 4 3
3 4 2
1 2 2
6 7 1
1 4 1
*/
8.5最短路径
Dijkstra 是一种经典的用于求解带权图最短路径问题的贪心算法。
该算法维护两个点集S和V-S,其中S表示已确定最短路径的节点集合,V-S则为未知最短路径的节点集合。算法每次从集合V-S中选择一个距离源点(s)最近的节点u加入到S中,并更新源点s到其他节点之间的最短路径。
具体实现过程如下:
1.定义数组dis[i] 表示源点s到i的最短路径长度,初始时将dis[s]赋值为0,其他节点的dis数组值设置为正无穷大。 2.定义visited[i]数组表示节点i在当前时刻是否已确定了最短路径,初始将visited[s]置为true。 3.重复下述步骤(直至所有节点都已确定最短路径) a) 从未确定最短路径的节点集合V-S中找出路径最短的一个节点u,并将其加入到S中。 b) 对于节点u的所有邻接节点v,如果通过节点u到达节点v的路径长度小于当前记录的最短路径,则更新dis[v]的值。 c) 重复执行a)、b)两步操作,直到所有节点均已确定最短路径。
经过以上操作后,dis数组中存储的即为源点s到各个节点的最短路径长度。
Dijkstra
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 10010; // 定义节点个数的最大值
const int INF = 0x3f3f3f3f; // 定义正无穷
int cost[MAXN][MAXN], d[MAXN]; //d里面存储的是到各个结点的最短距离 cost储存的是各边的长度
bool vis[MAXN];
void dijkstra(int s, int n) //n是总结点数 s是从哪个结点开始
{
for (int i = 1; i <= n; i++)
d[i] = cost[s][i];
memset(vis, 0, sizeof(vis));
vis[s] = true;
for (int i = 1; i < n; i++)
{
int u = -1;
for (int j = 1; j <= n; j++)
if (!vis[j] && (u == -1 || d[u] > d[j])) //寻找两块之间最小的边
u = j;
vis[u] = true;
for (int v = 1; v <= n; v++)
d[v] = min(d[v], d[u] + cost[u][v]);
}
}
int main()
{
int n, m, s;
cin>>n>>m>>s; //n是结点数 m是边数 s是开始的结点
memset(cost, INF, sizeof(cost)); // 初始化邻接矩阵
while (m--)
{
int u, v, w;
cin>>u>>v>>w;
cost[u][v] = w; // 输入有向边及其权值
}
dijkstra(s, n);
for (int i = 1; i <= n; i++)
printf("%d到%d的距离是%d",s,i,d[i]);
return 0;
}
拓扑排序(有环的有向图,一定不存在拓扑序)
#include<bits/stdc++.h>
using namespace std;
const int MAXN=100;
int Graph[MAXN][MAXN];//图的邻接矩阵
int indegree[MAXN];//每个顶点的入度
int sortedList[MAXN];//存拓扑排序的结果
void topo(int n)
{
int counter=0;//记录排好序的顶点数量
//初始化每个顶点的入度数组
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
if(Graph[j][i]!=0)//j到i有边
{
indegree[i]++;//i的入度+1;
}
}
}
//
int queue[MAXN];
int front=0,end=-1;
for(int i=0; i<n; i++)
{
if(indegree[i]==0)
{
queue[end]=i;
end++;
}
}
//开始进行拓扑排序
while(front<=end)
{
int cur=queue[front];//取队头元素
front++;
sortedList[counter]=cur;//加入结果序列
counter++;
//再把相关联的边删去,相关联的结点的度-1
for(int i=0; i<n; i++)
{
if(Graph[cur][i]!=0)
{
indegree[i]--;
if(indegree[i]==0)
{
queue[++end]=i;
}
}
}
}
if(counter!=n)//说明存在回路
{
cout<<"The Graph has a circle.\n";
}
else
{
for(int i=0; i<n; i++)
{
cout<<sortedList[i]+1<<" "; //输出拓扑排序的结果(注意要将结点编号+1,因为系统从0开始)
}
cout<<endl;
}
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=0; i<m; i++)
{
int u,v;
cin>>u>>v;
Graph[u-1][v-1]=1;
}
topo(n);
return 0;
}
/*
9 11
2 5
5 6
2 4
4 6
2 3
3 4
1 3
4 7
1 8
8 9
9 7
1 2 8 3 5 9 4 6 7
*/

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








