Excel实现简单仿真功能——新品投放市场盈利能力模型

一、问题

某公司想研究开发某一款新产品的盈利能力。

1.新产品研发的固定成本是随机的 服从正态分布, 均值 $2.2 billion（即2,200,000,000），标准差 $0.3 billion（即300,000,000） 固定成本只发生在第1年的开始。

2.第1年生产的单位变动成本服从正态分布, 均值 $7200, 标准差 $250。 从第2年到第5年，每一年的单位变动成本都等于前一年的变动成本乘以一个通货膨胀因子 每一年的通货膨胀因子都服从正态分布，且相互独立，均值1.05 (即平均5%增长) ，标准差0.02。

3.第1年汽车的销售单价为$13,000。 从第2年到第5年，每一年汽车的销售单价都等于前一年的销售单价乘以通货膨胀因子（成本和售价对应的因子相同）。

4.第1年的汽车需求服从正态分布，均值 100,000，标准差 20,000 。第2-5年，需求服从正态分布，均值为前一年的实际需求，标准差 20,000。

5.在年份 y，公司的生产量为年份 y 的期望需求 加上年份 y 需求的标准差，如果某一年的生产量大于实际需求，GF公司会在年末以30%的折扣打折销售剩余汽车。

6.现在需要通过Excel仿真了解未来五年内该产品投入市场后的盈利能力。（思路：通过生成随机数模拟需求、成本等自然变化）200次试验（replication），每次试验包含5年。 计算每次试验的5年总利润 计算200次试验下利润的均值、标准差、期望利润的95%置信区间。 生成5年总利润的频率表、直方图。

二、Excel单次仿真操作

1.单位可变成本与销售价格的生成

①首先生成第一年的单位可变成本与销售价格，第1年生产的单位可变成本服从正态分布, 均值 $7200, 标准差 $250，首先用Rand()函数生成200个0-1之间的随机数，再用NORM.INV函数生成200个服从均值 $7200, 标准差 $250正态分布的随机变量，用以模拟可变成本的分布。第一年的销售单价为￥13000，保持不变。

②第2-5年，可变成本与销售价格是前一年的值乘以通货膨胀因子，且通货膨胀因子服从均值1.05 ，标准差0.02的正态分布。继续使用Rand()函数，生成200个随机数，调用NORM.INV函数生成200个服从均值1.05 ，标准差0.02正态分布的随机变量，用以表示通货膨胀因子。

③通货膨胀因子生成完毕后，第二年的可变成本为前一年可变成本乘以今年的通货膨胀因子；第二年的销售单价为前一年的销售单价乘以今年的通货膨胀因子，且可变成本与销售单价乘以的是同一个通货膨胀因子，因此这里不需要生成两次随机数和随机变量。

④第3-5年的可变成本与销售单价生成方式与上述相同，按照

生成随机数→生成通货膨胀因子→用当年的通货膨胀因子乘以去年的数值→生成当年可变成本/销售单价

的顺序不断进行迭代，最终可以得到五年中每一年的通货膨胀因子、销售单价、可变成本。

2.需求与生产量的生成

①第一年产品需求服从正态分布，均值 100,000，标准差 20,000，调用Rand()函数和NORM.INV函数生成200个随机变量表示第一年的需求。

生产量为当年需求的期望+需求的标准差，因此第一年的生产量为均值100000+20000=120000保持不变，不随随机因素变动。

②第2-5年的需求服从正态分布，均值为前一年的实际需求，标准差 20,000。在第二年表格Expected Demand一栏输入上一年需求的实际值，再新建一列生成200个随机数，用NORM.INV函数，概率选择前面生成的随机数，均值选择Expected Demand对应的数值，标准差为20000，生成200个随机变量表示第二年的实际需求，第3-5年也以此类推，将上一年需求的实际值作为这一年正态分布的均值，标准差保持20000不变，以此生成每一年的实际需求。

③第2-5年的生产量为当年的需求期望+需求标准差，而当年的需求期望是上一年的需求实际值，因此当年的生产量应该为去年的需求实际值+标准差20000，每一年都以此类推，生成生产量的值。

3.固定成本的生成

①固定成本服从正态分布, 均值 $2.2 billion（即2,200,000,000），标准差 $0.3 billion（即300,000,000），且只发生在一年。调用RAND()函数和NORM.INV函数生成200个服从（2.2billion,0.3biliion）正态分布的随机变量，表示固定成本。

4.计算收益

①计算完每一年的可变成本、销售单价、实际需求、生产量之后，可以用这些数值计算每一年的收益（不包括固定成本），如果生产量大于实际需求，公司会在年末以30%的折扣打折销售剩余汽车，因此总体收益应该为销售额减去总体可变成本再加上打折卖出汽车的收入

每一年的收益计算公式为：

收益=MIN（生产量，实际需求）*销售单价-可变成本*生产量+MAX（生产量-实际需求，0）*销售单价*折扣

②由于在第1-5年的多次迭代后，实际需求出现了为负数的情况，为了避免实际需求为负时收益计算不准确，因此在计算收益时加上了IF条件语句，即当实际需求大于零时，按照上述公式计算收益，当需求小于零时，按照需求等于0计算，这时收益为将生产出的所有产品按折扣卖掉后减去总体可变成本，用于表示由于没有需求而造成的损失。

最终输入到Excel中的收益公式计算如下：

收益=IF（实际需求>0，MIN（生产量，实际需求）*销售单价-单位可变成本*生产量+MAX（生产量-实际需求，0）*销售单价*折扣比例，生产量*销售单价*折扣-生产量*单位可变成本）

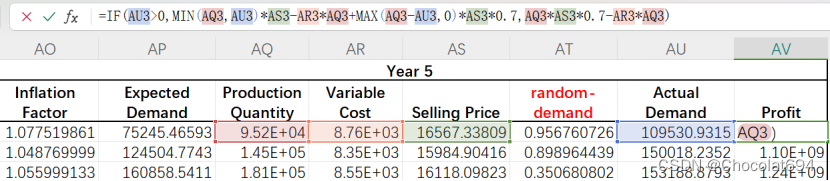
③五年总收益的计算。按照上述方法和公式计算完每一年收益后，需要计算这五年的总体收益，也就是该项目投入后的净利润。在将五年收益相加后，还需要减去固定成本，才是最终五年的总收益。

三、结果

1.总收益的平均值、方差、置信区间

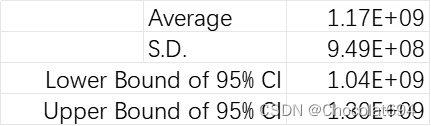
项目总收益在200次模拟中有正有负，也就是既有盈利的情况也有亏钱的情况，将这200次模拟得到的总收益计算平均值、方差以及95%的置信区间，得到收益分布的结果。

（上图为不断更新过程中的示例）

通过f9键不断更新模拟结果：

①平均值为正数，没有出现过负数的情况，大多分布在1.0E+09到1.25E+09之间，少数情况小于1.0E+09或者大于1.25E+09。

②标准差则基本在8.5E+08到1.0E+09区间内变动。

③95%置信区间的长度一般保持在0.3E+09左右，区间上界在1.0E+09左右，区间下界在1.3E+09左右，上下界的分布并未出现明显的大范围波动。

2.总收益的频率分布表、直方图，未盈利概率

用Frequency函数获取总收益在不同区间分布的频率，计算收益小于零所占的比例，并生成图表，按f9更新，观察趋势。

（上图为模拟过程中出现的频率图示例）

①未盈利百分比在不断模拟的过程中大多分布在8%-12%区间内，少数情况出现了6.5%、7.5%、11.5%、12.5%，极少数极端情况出现了15%、16%。

②从频率分布图来看，总收益在-1.00E+09到4.00E+09之间总体呈现对称分布，偶尔会近似形成正态分布、三角分布；少数情况会呈现轻度左偏或右偏。概率最大的收益大约在1.00E+09到2.0E+09之间。

四、结论

①从平均值、置信区间和盈利比率来看，总收益的期望在多次模拟和不断更新后依然保持为正数，且期望总收益在10位数量级；95%的置信区间没有出现过下界小于等于零的情况，且基本可以看作在1.0E+09到1.3E+09之间，这意味着在95%的水平上企业是能盈利的，且盈利数额大约分布在1.0E+09到1.3E+09左右，盈利规模和量级在10位数（十亿级别）。将仿真模拟的未盈利比率近似看作未盈利概率，该公司盈利的概率在85%-90%之间，盈利的可能性非常高。

②尽管该项目的收益平均值、95%置信区间表现乐观，表明该项目有足够信心盈利，但是从标准差来看，标准差在9位数量级，甚至有十分接近平均值的情况，这意味着该项目的盈利情况波动幅度较大，受到现实中随机因素的干扰程度高，表明投资该项目也具有一定的风险；该公司需要在风险和收益两个方面充分权衡，考虑是否能承担10%-15%可能性的亏损风险，做出是否开发新产品的决策。

③尽管该项目盈利概率大，且盈利数额最有可能集中在10位数量级，但是盈利收入的具体数额波动也非常大，公司需要考虑这个量级（十亿级别）的收入是否值得投资，与公司整体战略、总体体量比起来，是否有足够的资金周转完成项目开发以及是否愿意承担风险。

五、拓展——Excel模拟表计算

上文中的计算方法仅仅支持一次仿真实验，如果改变其中某个参数则全部需要重新计算一遍，因此可以采用Excel的模拟表计算功能，在改变参数情况下快速获得结果。

1.确定模拟表区域，按照上文的流程汇总到一个区域中，并记录参数和结果。

2.在数据-模拟分析点击之后就会出现模拟运算表，选择需要填入数据的表格范围，再选择，引入行引用的单元格（比如在行上面是列出的不同的固定成本，那么引用的单元格就是之前模拟计算区域所引用的固定成本单元格，模拟计算区域引用的固定成本只能是一个）

运行成功后就可以看到在不同参数取值时的模拟运算结果，不断更新随机数生成，总结平均值、方差可以对比参数不同时的结果。