线性回归算法笔记（2）

摘要：对于上一篇博客（HERE）本文使用torch.nn算法库，实现线性回归模型。此外，补充了梯度下降算法的底层逻辑。

0、问题描述

---

假设特征向量为$w$（设为$[-2,-3.4{]}^T$），$b=4.2$，样本为$X$，输出为$y$，同时加上一点噪声$ϵ$：

$$y=Xw+b+ϵ$$

后续就是要通过对大量$X,y$关系的学习探索$w,b$的取值。

1、数据集构建与初始化

---

定义真实的$w,b$参数，使用d2l算法库生成1000条高斯分布加噪声的随机数据作为训练集：

import numpy as np
import d2l
from d2l import torch as d2l
import torch
from torch.utils import data

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

构造一个pytorch数据迭代器。每轮次随机选取一定数目的训练数据。这样以后，就可以实现批量化训练：

def load_array(data_arrays, batch_size, is_train=True):
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size=10
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter))

输出如下：

[tensor([[ 1.7709,  0.8762],
         [-0.5039, -0.5574],
         [ 1.7404, -0.6892],
         [ 0.1441, -0.0245],
         [-0.9593, -0.8841],
         [-1.1815, -0.2625],
         [-0.8406,  0.4300],
         [-1.4473,  0.7672],
         [-1.9178,  0.1378],
         [ 1.5084, -0.6536]]),
 tensor([[ 4.7558],
         [ 5.0965],
         [10.0296],
         [ 4.5651],
         [ 5.2905],
         [ 2.7396],
         [ 1.0720],
         [-1.3107],
         [-0.1215],
         [ 9.4347]])]

2、定义模型

---

首先，使用nn模组定义模型、初始化参数：

import torch.nn
# 定义模型
model = nn.Sequential(nn.Linear(2, 1))

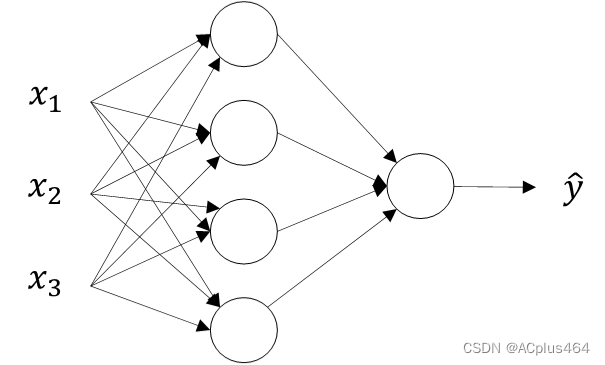
• nn.Sequencial是可以作为一个容器，封装若干个模型，比如nn.Linear()等。训练时让数据依次通过这些模型。
• nn.Linear(2, 1)即定义了一个拥有2个特征和1个标签的线性回归网络，也就是全连接层。

# 初始化模型参数
model[0].weight.data.normal_(0, 0.01)
model[0].bias.data.fill_(0)

此处为重点使用方法。

• model[0]访问到了第一层网络即定义的Linear层；
• model[0].weight是该层网络的所有权重形成的tensor。例如，对于nn.Linear(2, 1)而言，它初始weight就是tensor([[-0.0026, -0.0009]], requires_grad=True)；
• .data表示访问权重张量的底层数据（tensor）。例如，对于nn.Linear(2, 1)而言，它初始weight.data就是tensor([[-0.0026, -0.0009]]；
• .fill_(0)对偏置张量的底层数据进行就地（in-place）操作，将所有元素的值填充为0。

# 定义损失函数
loss = nn.MSELoss()

还是使用之前提到的均方误差损失，这也是最常用的损失函数之一。

# 定义优化算法的实现，需要传入2个参数
trainer = torch.optim.SGD(model.parameters(), lr=0.03)

为了定义优化算法，我们传入模型（全部layer）的全部参数和学习率，从而进行随机梯度下降。

3、训练过程

---

线性回归算法笔记（1）中有所提及，此处基本不变，不赘述。

num_epochs=3
for epoch in range(num_epochs):
    for X,y in data_iter:
        l = loss(model(X), y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    with torch.no_grad():
        l = loss(model(features), labels)
        print(f'epoch {epoch+1}, loss {l:f}')

4、补充内容：梯度下降算法的底层逻辑

---

4.1 基本概念

梯度：对于多元函数$L(x_1,x_2,...,x_n)$，其梯度是一个向量，记作$\nabla L$，即为函数变化率最大的方向和数值。有如下定义：$$\nabla L=\left(\frac{\partial L}{\partial x_1},\frac{\partial L}{\partial x_2},...,\frac{\partial L}{\partial x_n}\right)$$

例如，$L(x,y)=x^2+2y^2$，则$\nabla L=(2x,4y)$。

4.2 算法实现

假如初始时刻$L$上某点$P(x_{10},x_{20},...,x_{n0})$，我们需要让它运动到函数的极小值点处：

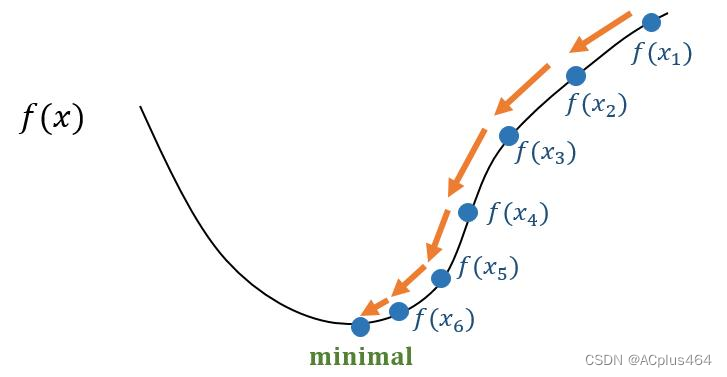
为了实现这一目的，我们可以进行多轮迭代。每一次迭代，都让$P$朝着梯度的反方向运动一定的距离。设学习率为$ϵ$，那么$P$的运动量可以设置成$ϵ\nabla L_P$。直到$P$的梯度值趋近于0，迭代结束。

为此，可以设置一个迭代结束的条件，比如：当梯度值$|\nabla L_P|$小于某个很小的值时，就结束该过程。

4.3 机器学习中的实际应用

对于机器学习，我们将损失函数$L$视作关于模型全部参数$\theta =({\theta }_1,{\theta }_2,...,{\theta }_n)$的函数（事实上也的确如此，这是可以证明的），即$L({\theta }_1,{\theta }_2,...,{\theta }_n)$。

那么，每epoch或batch训练完得到一组参数$\theta$都要根据此时其在损失函数$L(\theta )$上的位置，以梯度下降的算法迭代若干次到最低点，由此作为本轮此训练结束后的参数权值更新过程。

⭐都看到这里啦，不如点个免费的赞吧~