回归算法笔记

基本含义：

线性回归是一种有监督算法。

在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。

通俗点，线性回归的学习就是找到一个函数，使其能很好的拟合已知函数且很好的预测未知数据。
也可以理解为，期望所有数据比较均匀的分布在直线或者平面的两侧。

线性回归又分为
为了找到这个函数， 引用损失函数loss。
借用网络图片， 左侧图片为原始数据集， 右侧的直线是找到的一条loss值最小的直线， 使得该直线能很好的拟合原始数据集。

目标函数

线性回归包括一元线性回归，二元线性回归 和多元线性回归， 他们之间本质是一样的， 区别就是一元线性回归的目标函数是一元线性函数， 二元线性回归的目标函数是二元线性函数， 多元线性回归的目标函数是多元线性函数。
解释一下， 目标函数就是要找到 的最佳的函数。
通常我们定义目标函数如下：
它既可以表示一元线性函数，也可以表示多元线性函数。

公式中最后结果 ：Xθ， 一般理解为矩阵相乘。

损失函数loss

我们将上述的目标函数写成损失形式：

注释：
y^(i) —表示第i个样本的实际值，也可称为标签值
θ^(T)—表示参数θ的转置（是否需要转置要看初始设置θ的形状）
x^(i)—表示第i个样本的x数据， θx为第i个样本预测值
ε^(i)—表示第i个样本的差值，即， 真实值-预测值

线性回归模型最优的时候是所有样本的预测值和实际值之间的差值最小化，由于预测值和实际值之间的差值存在正负性，所以要求平方后的值最小化。也就是可以得到如下的一个目标函数：

现在的目标求出一个矩阵θ， 使得损失函数loss的值最小。
于是引入最小二乘法 和 梯度下降法：

最小二乘法:

---

最小二乘法可以参考同济大学出版的工程数学《线性代数》
也可参考其他博客写的最小二乘法： https://blog.csdn.net/lql0716/article/details/70165695.
刘建平的博客也写的很好：https://www.cnblogs.com/pinard/p/5976811.html
这里只给推倒公式：

公式中均为矩阵，这里引入一些矩阵的求导，

当损失函数loss取极小值时， 其梯度=0

注意：
只有当X^（T）X存在逆矩阵时，才能使用最小二乘法上述公式，为了避免这一麻烦， 我们通常添加一个λ倍的单位矩阵来优化此公式，

当然， 采用这种优化的时候，降低了部分精度， 但是无伤大雅。

优点:
1.无需像梯度下降法一样一步一步迭代更新，可直接求出目标θ的值.

缺点：
1.如果拟合函数不是线性的，这时无法使用最小二乘法，需要通过一些技巧转化为线性才能使用， 这时推荐用梯度下降法。
2.当样本特征n非常的大的时候，计算X^(T)X的逆矩阵是一个非常耗时的工作（nxn的矩阵求逆），甚至不可行。

一段简单的使用最小二乘法的代码：

import numpy as np
import matplotlib.pyplot as plt


# 1. 构造数据X, Y
x = np.array([
            [10], [15], [20], [30], [50], [60], [60], [70]
             ], dtype=np.float)
y = np.array([
            [0.8], [1.0], [1.8], [2], [3.2], [3], [3.1], [3.5]
             ], dtype=np.float)

# 2.为方便求解矩阵的逆,将numpy数组转化成矩阵对象
X = np.mat(x)
Y = np.mat(y)
I = (X.T * X).I   # 矩阵的逆, 要求数据类型必须是matrix(矩阵对象)
print('X.T * X矩阵的逆:', (X.T * X).I)

# 3. 参数求解
o = I * X.T * Y
o = o[0,0]
print(o)

plt.scatter(x, y)
x = np.linspace(10, 70)
print(x)
y = o*x
plt.plot(x,y)
plt.show()

运行结果：
X.T * X矩阵的逆: [[6.1633282e-05]]
0.05485362095531587
图片:

梯度下降法:

---

由于之前已经详细写过梯度下降法， 这里就不在重复写了。
有兴趣请看之前写的梯度下降法， 链接
也可参考其他大牛写的博客~

线性回归的过拟合

---

原因：
原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点

解决办法：
为了防止数据过拟合，也就是的θ值在样本空间中不能过大，可以在目标函数之上增加一个正则项。正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。
正则项一般使用L1正则和 L2正则，

• L1正则化是指权值向量θ中各个元素的绝对值之和，通常表示为∣∣θ∣∣1
• L2正则化是指权值向量θ中各个元素的平方和然后再求平方根，通常表示为∣∣θ∣∣2

正则化后的损失函数如下图：

岭回归 和 LASSO回归

---

使用L2正则的线性回归模型就称为Ridge回归(岭回归)
也就是添加L2正则化的损失函数，构建的线性回归：

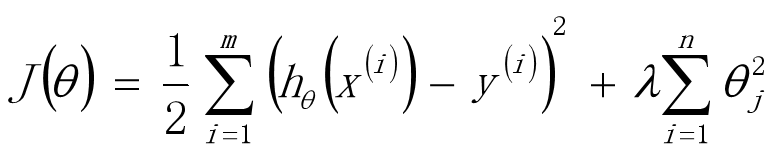
使用L1正则的线性回归模型就称为LASSO回归(Least Absolute Shrinkage and Selection Operator)
也就是添加L1正则化的损失函数，构建的线性回归：

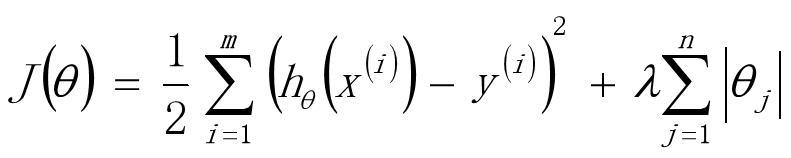
岭回归：回归得到的回归系数更符合实际，更可靠。另外，能让
估计参数的波动范围变小，变的更稳定。在存在病态数据偏多的研
究中有较大的实用价值。

L2-norm中，由于对于各个维度的参数缩放是在一个圆内缩放的，不可能导致有维度参数变为0的情况，那么也就不会产生稀疏解；实际应用中，数据的维度中是存在噪音和冗余的，稀疏的解可以找到有用的维度并且减少冗余，提高后续算法预测的准确性和鲁棒性

L1-norm可以达到最终解的稀疏性的要求

Ridge模型具有较高的准确性、鲁棒性以及稳定性(冗余特征已经被删除了)；LASSO模型具有较高的求解速度。

note：
sklearn中有完美的线性回归，岭回归 和 LASSO回归的API， 熟悉原理后可直接调用API：
线性回归：sklearn.linear_model.LinearRegression()

岭回归 ：sklearn.linear_model.Ridge(alpha=1.0)
alpha:正则化力度

岭回归 ：sklearn.linear_model.Lasso(alpha=1.0)
alpha:正则化力度

线性回归总结

---

1. 算法模型：线性回归(Linear)、岭回归(Ridge)、LASSO回归
2. 正则化：L1-norm、L2-norm
3. 损失函数/目标函数：
4. θ求解方式：最小二乘法(直接计算，目标函数是平方和损失函数)、梯度下降(MBGD)