一、实验目的
- (一)秉承 EIP-CDIO 的教学理念,以实验的方式,理解数值积分。
- (二)编写不同的数值积分算法,并用其计算所给的函数积分。
二、实验设备信息
- (一)设备信息:

-
(二)运行环境 : Python 3.8
-
(三)IDE : PyCharm Professional 2022.2.2
三、实验内容
(一)数值积分的基本思想

1.梯形公式

积分中值定理告诉我们,在积分区间
[
a
,
b
]
[a,b]
[a,b] 内存在一点
ζ
\zeta
ζ ,成立
∫
a
b
f
(
x
)
d
x
=
(
b
−
a
)
f
(
ζ
)
\int_a^b f(x) \mathrm{d} x=(b-a) f(\zeta)
∫abf(x)dx=(b−a)f(ζ)
就是说,底为
a
−
b
a-b
a−b 而高为
f
(
ζ
)
f(\zeta)
f(ζ) 的矩形面积恰等于所求曲边梯形的面积。我们将
f
(
ζ
)
f(\zeta)
f(ζ) 称为区间
[
a
,
b
]
[a,b]
[a,b] 上的平均高度,如果用两端点的“高度”
f
(
a
)
f(a)
f(a) 与
f
(
b
)
f(b)
f(b) 的算数平均值作为平均高度
f
(
ζ
)
f(\zeta)
f(ζ) 的近似值,这样导出的求积公式
∫
a
b
f
(
x
)
d
x
≈
b
−
a
2
[
f
(
a
)
+
f
(
b
)
]
(
1.1
)
\int_a^b f(x) \mathrm{d} x \approx \frac{b-a}{2}[f(a)+f(b)] \quad\quad\quad (1.1)
∫abf(x)dx≈2b−a[f(a)+f(b)](1.1)
便是梯形公式。
2.矩形公式
如果将梯形公式改用区间中点
c
=
a
+
b
2
c=\frac{a+b}{2}
c=2a+b 的“高度”
f
(
c
)
f(c)
f(c) 近似地取代平均高度
f
(
ζ
)
f(\zeta)
f(ζ) ,则又可导出所谓中矩形公式(简称矩形公式)
∫
a
b
f
(
x
)
d
x
≈
(
b
−
a
)
f
(
a
+
b
2
)
(
1.2
)
\int_a^b f(x) \mathrm{d} x \approx(b-a) f\left(\frac{a+b}{2}\right) \quad\quad\quad (1.2)
∫abf(x)dx≈(b−a)f(2a+b)(1.2)
3.基本形式
更一般地,在区间
[
a
,
b
]
[a,b]
[a,b] 上适当选取某些节点
x
k
x_{k}
xk ,然后用
f
(
x
k
)
f(x_{k})
f(xk) 的加权平均得到平均高度
f
(
ζ
)
f(\zeta)
f(ζ) 的近似值,这样构造出的求积公式具有下列形式:
∫
a
b
f
(
x
)
d
x
≈
∑
k
=
0
n
A
k
f
(
x
k
)
(
1.3
)
\int_a^b f(x) \mathrm{d} x \approx \sum_{k=0}^n A_k f\left(x_k\right) \quad\quad\quad (1.3)
∫abf(x)dx≈k=0∑nAkf(xk)(1.3)
式中
x
k
x_{k}
xk 称为求积节点;
A
k
A_{k}
Ak 称为求积系数,亦称伴随节点
x
k
x_{k}
xk 的权。权
A
k
A_{k}
Ak 仅仅与节点
x
k
x_{k}
xk 的选取有关,而不依赖于被积函数
f
(
x
)
f(x)
f(x) 的具体形式。
(二)代数精度的概念
如果某个求积公式对于次数不超过 m m m 的多项式均能准确地成立,但对于 m + 1 m+1 m+1 次多项式就不准确成立,则称该求积公式具有 m m m 次代数精度(或代数精确度)。
一般地,如果想让求积公式
(
1.3
)
(1.3)
(1.3) 具有
m
m
m 次代数精度,只要令它对于
f
(
x
)
=
1
,
x
,
…
,
x
m
f(x)=1,x,\dots,x^{m}
f(x)=1,x,…,xm 都能准确成立,这就要求
{
∑
A
k
=
b
−
a
∑
A
k
x
k
=
1
2
(
b
2
−
a
2
)
⋮
∑
A
k
x
k
m
=
1
m
+
1
(
b
m
+
1
−
a
m
+
1
)
(
1.4
)
\left\{\begin{array}{l} \sum A_k=b-a \\ \sum A_k x_k=\frac{1}{2}\left(b^2-a^2\right) \\ \vdots \\ \sum A_k x_k^m=\frac{1}{m+1}\left(b^{m+1}-a^{m+1}\right) \end{array}\right. \quad\quad\quad (1.4)
⎩⎪⎪⎪⎨⎪⎪⎪⎧∑Ak=b−a∑Akxk=21(b2−a2)⋮∑Akxkm=m+11(bm+1−am+1)(1.4)
如果我们事先选定求积节点
x
k
x_{k}
xk ,譬如,以区间
[
a
,
b
]
[a,b]
[a,b] 的等距分点作为节点,这时取
m
=
n
m=n
m=n 求解线性方程组
(
1.4
)
(1.4)
(1.4) 即可确定求积系数
A
k
A_{k}
Ak ,而使求积公式
(
1.3
)
(1.3)
(1.3) 至少具有
n
n
n 次代数精度。
1.求积公式的余项
若求积公式
(
1.3
)
(1.3)
(1.3) 的代数精度为
m
m
m ,则由求积公式余项的表达式可将余项表示为
R
[
f
]
=
∫
a
b
f
(
x
)
d
x
−
∑
k
=
0
n
A
k
f
(
x
k
)
=
K
f
(
m
+
1
)
(
η
)
(
1.8
)
R[f]=\int_a^b f(x) \mathrm{d} x-\sum_{k=0}^n A_k f\left(x_k\right)=K f^{(m+1)}(\eta) \quad\quad\quad (1.8)
R[f]=∫abf(x)dx−k=0∑nAkf(xk)=Kf(m+1)(η)(1.8)
其中
K
K
K 为不依赖于
f
(
x
)
f(x)
f(x) 的待定参数,
η
∈
(
a
,
b
)
\eta\in(a,b)
η∈(a,b) 。这个结果表明当
f
(
x
)
f(x)
f(x) 是次数小于等于
m
m
m 的多项式时,由于
f
m
+
1
(
x
)
=
0
f^{m+1}(x)=0
fm+1(x)=0 ,故此时
R
[
f
]
=
0
R[f]=0
R[f]=0 ,即求积公式
(
1.3
)
(1.3)
(1.3) 准确成立。而当
f
(
x
)
=
x
m
+
1
f(x)=x^{m+1}
f(x)=xm+1 时,
f
m
+
1
(
x
)
=
(
m
+
1
)
!
f^{m+1}(x)=(m+1)!
fm+1(x)=(m+1)! ,
(
1.8
)
(1.8)
(1.8) 式的左端
R
n
(
f
)
≠
0
R_{n}(f)\not=0
Rn(f)=0 ,故可求得
K
=
1
(
m
+
1
)
!
[
∫
a
b
x
m
+
1
d
x
−
∑
k
=
0
n
A
k
x
k
m
+
1
]
=
1
(
m
+
1
)
!
[
1
m
+
2
(
b
m
+
2
−
a
m
+
2
)
−
∑
k
=
0
n
A
k
x
k
m
+
1
]
(
1.9
)
\begin{aligned} K &=\frac{1}{(m+1) !}\left[\int_a^b x^{m+1} \mathrm{~d} x-\sum_{k=0}^n A_k x_k^{m+1}\right] \\ &=\frac{1}{(m+1) !}\left[\frac{1}{m+2}\left(b^{m+2}-a^{m+2}\right)-\sum_{k=0}^n A_k x_k^{m+1}\right] \end{aligned} \quad\quad\quad (1.9)
K=(m+1)!1[∫abxm+1 dx−k=0∑nAkxkm+1]=(m+1)!1[m+21(bm+2−am+2)−k=0∑nAkxkm+1](1.9)
带入余项
(
1.8
)
(1.8)
(1.8) 式中可以得到具体的余项表达式。
(三)插值型求积公式
1.基本概念
设给定一组节点
a
⩽
x
0
<
x
1
<
x
2
<
⋯
<
x
n
⩽
b
a \leqslant x_0<x_1<x_2<\cdots<x_n \leqslant b
a⩽x0<x1<x2<⋯<xn⩽b
且已知函数
f
(
x
)
f(x)
f(x) 在这些节点上的值,作插值函数
L
n
(
x
)
=
∑
k
=
0
n
y
k
l
k
(
x
)
L_n(x)=\sum_{k=0}^n y_k l_k(x)
Ln(x)=∑k=0nyklk(x) 。由于代数多项式
L
n
(
x
)
L_{n}(x)
Ln(x) 的原函数是容易求出的,我们取
I
n
=
∫
a
b
L
n
(
x
)
d
x
I_n=\int_a^b L_n(x) \mathrm{d} x
In=∫abLn(x)dx
作为积分
I
=
∫
a
b
f
(
x
)
d
x
I=\int_a^b f(x) \mathrm{d} x
I=∫abf(x)dx 的近似值,这样构造出的求积公式
I
n
=
∑
k
=
0
n
A
k
f
(
x
k
)
(
1.5
)
I_n=\sum_{k=0}^n A_k f\left(x_k\right) \quad\quad\quad (1.5)
In=k=0∑nAkf(xk)(1.5)
称为是插值型的,式中求积系数
A
k
A_{k}
Ak 通过插值基系数
l
k
(
x
)
l_{k}(x)
lk(x) 积分得出,即
A
k
=
∫
a
b
l
k
(
x
)
d
x
,
k
=
0
,
1
,
⋯
,
n
.
(
1.6
)
A_k=\int_a^b l_k(x) \mathrm{d} x, \quad k=0,1, \cdots, n . \quad\quad\quad (1.6)
Ak=∫ablk(x)dx,k=0,1,⋯,n.(1.6)
2.牛顿-科特斯公式
- 科特斯系数与辛普森公式
将积分区间
[
a
,
b
]
[a,b]
[a,b] 划分为
n
n
n 等分,步长
h
=
b
−
a
n
h=\frac{b-a}{n}
h=nb−a ,选取等距节点
x
k
=
a
+
k
h
x_{k}=a+kh
xk=a+kh 构造出的插值型求积公式
I
n
=
(
b
−
a
)
∑
k
=
0
n
C
k
(
n
)
f
(
x
k
)
(
2.1
)
I_n=(b-a) \sum_{k=0}^n C_k^{(n)} f\left(x_k\right) \quad\quad\quad (2.1)
In=(b−a)k=0∑nCk(n)f(xk)(2.1)
称为牛顿-科特斯公式,式中的
C
k
(
n
)
C_{k}^{(n)}
Ck(n) 称为科特斯系数。按
(
1.6
)
(1.6)
(1.6) 式,引进变换
x
=
a
+
t
h
x=a+th
x=a+th ,则有
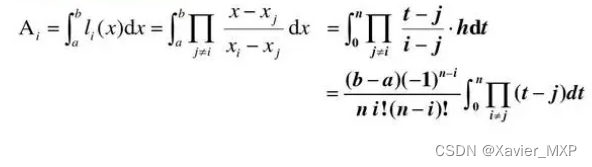
由于是多项式的积分,科特斯系数的计算不会遇到实质性的困难。
当
n
=
1
n=1
n=1 时,
C
0
(
1
)
=
C
1
(
1
)
=
1
2
C_{0}^{(1)}=C_{1}^{(1)}=\frac{1}{2}
C0(1)=C1(1)=21
这时的求积公式就是我们所熟悉的梯形公式
(
1.1
)
(1.1)
(1.1) 。
当
n
=
2
n=2
n=2 时,按
(
2.2
)
(2.2)
(2.2) 式,这时的科特斯系数为
C
0
(
2
)
=
1
4
∫
0
2
(
t
−
1
)
(
t
−
2
)
d
t
=
1
6
C
1
(
2
)
=
−
1
2
∫
0
2
t
(
t
−
2
)
d
t
=
4
6
C
2
(
2
)
=
1
4
∫
0
2
t
(
t
−
1
)
d
t
=
1
6
\begin{aligned} &C_0^{(2)}=\frac{1}{4} \int_0^2(t-1)(t-2) \mathrm{d} t=\frac{1}{6} \\ &C_1^{(2)}=-\frac{1}{2} \int_0^2 t(t-2) \mathrm{d} t=\frac{4}{6} \\ &C_2^{(2)}=\frac{1}{4} \int_0^2 t(t-1) \mathrm{d} t=\frac{1}{6} \end{aligned}
C0(2)=41∫02(t−1)(t−2)dt=61C1(2)=−21∫02t(t−2)dt=64C2(2)=41∫02t(t−1)dt=61
相应的求积公式是下列辛普森公式:
S
=
b
−
a
6
[
f
(
a
)
+
4
f
(
a
+
b
2
)
+
f
(
b
)
]
(
2.3
)
S=\frac{b-a}{6}\left[f(a)+4 f\left(\frac{a+b}{2}\right)+f(b)\right] \quad\quad\quad (2.3)
S=6b−a[f(a)+4f(2a+b)+f(b)](2.3)

当
n
=
4
n=4
n=4 时的牛顿-科特斯公式则特别称为科特斯公式,其形式是
C
=
b
−
a
90
[
7
f
(
x
0
)
+
32
f
(
x
1
)
+
12
f
(
x
2
)
+
32
f
(
x
3
)
+
7
f
(
x
4
)
]
(
2.4
)
C=\frac{b-a}{90}\left[7 f\left(x_0\right)+32 f\left(x_1\right)+12 f\left(x_2\right)+32 f\left(x_3\right)+7 f\left(x_4\right)\right] \quad\quad\quad (2.4)
C=90b−a[7f(x0)+32f(x1)+12f(x2)+32f(x3)+7f(x4)](2.4)
这里
h
=
b
−
a
4
h=\frac{b-a}{4}
h=4b−a ,
x
k
=
a
+
k
h
(
k
=
0
,
1
,
2
,
3
,
4
)
.
x_{k}=a+kh(k=0,1,2,3,4).
xk=a+kh(k=0,1,2,3,4).
表-1 列出科特斯系数表的一部分。
| n n n | C k ( n ) C_{k}^{(n)} Ck(n) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 2 \frac{1}{2} 21 | 1 2 \frac{1}{2} 21 | ||||||
| 2 | 1 6 \frac{1}{6} 61 | 2 3 \frac{2}{3} 32 | 1 6 \frac{1}{6} 61 | |||||
| 3 | 1 8 \frac{1}{8} 81 | 3 8 \frac{3}{8} 83 | 3 8 \frac{3}{8} 83 | 1 8 \frac{1}{8} 81 | ||||
| 4 | 7 90 \frac{7}{90} 907 | 16 45 \frac{16}{45} 4516 | 2 15 \frac{2}{15} 152 | 16 45 \frac{16}{45} 4516 | 7 90 \frac{7}{90} 907 | |||
| 5 | 19 288 \frac{19}{288} 28819 | 25 96 \frac{25}{96} 9625 | 25 144 \frac{25}{144} 14425 | 25 144 \frac{25}{144} 14425 | 25 96 \frac{25}{96} 9625 | 19 288 \frac{19}{288} 28819 | ||
| 6 | 41 840 \frac{41}{840} 84041 | 9 35 \frac{9}{35} 359 | 9 280 \frac{9}{280} 2809 | 34 105 \frac{34}{105} 10534 | 9 280 \frac{9}{280} 2809 | 9 35 \frac{9}{35} 359 | 41 840 \frac{41}{840} 84041 | |
| 7 | 751 17280 \frac{751}{17280} 17280751 | 3577 17280 \frac{3577}{17280} 172803577 | 1323 17280 \frac{1323}{17280} 172801323 | 2989 17280 \frac{2989}{17280} 172802989 | 2989 17280 \frac{2989}{17280} 172802989 | 1323 17280 \frac{1323}{17280} 172801323 | 3577 17280 \frac{3577}{17280} 172803577 | 751 17280 \frac{751}{17280} 17280751 |
(四)复合求积公式
1.复合梯形公式

将区间
[
a
,
b
]
[a,b]
[a,b] 划分为
n
n
n 等分,分点
x
k
=
a
+
k
h
,
h
=
b
−
a
n
,
k
=
0
,
1
,
…
,
n
x_{k}=a+kh,h=\frac{b-a}{n},k=0,1,\dots,n
xk=a+kh,h=nb−a,k=0,1,…,n ,在每个子区间
[
x
k
,
x
k
+
1
]
(
k
=
0
,
1
,
…
,
n
−
1
)
[x_{k},x_{k+1}](k=0,1,\dots,n-1)
[xk,xk+1](k=0,1,…,n−1) 上采用梯形公式
(
1.1
)
(1.1)
(1.1) ,则得
I
=
∫
a
b
f
(
x
)
d
x
=
∑
k
=
0
n
−
1
∫
x
k
x
k
+
1
f
(
x
)
d
x
=
h
2
∑
k
=
0
n
−
1
[
f
(
x
k
)
+
f
(
x
k
+
1
)
]
+
R
n
(
f
)
(
3.1
)
I=\int_a^b f(x) \mathrm{d} x=\sum_{k=0}^{n-1} \int_{x_k}^{x_{k+1}} f(x) \mathrm{d} x=\frac{h}{2} \sum_{k=0}^{n-1}\left[f\left(x_k\right)+f\left(x_{k+1}\right)\right]+R_n(f) \quad\quad\quad (3.1)
I=∫abf(x)dx=k=0∑n−1∫xkxk+1f(x)dx=2hk=0∑n−1[f(xk)+f(xk+1)]+Rn(f)(3.1)
记
T
n
=
h
2
∑
k
=
0
n
−
1
[
f
(
x
k
)
+
f
(
x
k
+
1
)
]
=
h
2
[
f
(
a
)
+
2
∑
k
=
1
n
−
1
f
(
x
k
)
+
f
(
b
)
]
(
3.2
)
T_n=\frac{h}{2} \sum_{k=0}^{n-1}\left[f\left(x_k\right)+f\left(x_{k+1}\right)\right]=\frac{h}{2}\left[f(a)+2 \sum_{k=1}^{n-1} f\left(x_k\right)+f(b)\right] \quad\quad\quad (3.2)
Tn=2hk=0∑n−1[f(xk)+f(xk+1)]=2h[f(a)+2k=1∑n−1f(xk)+f(b)](3.2)
称为复合梯形公式。
2.复合辛普森求积公式

将区间
[
a
,
b
]
[a,b]
[a,b] 分为
n
n
n 等分,在每个子区间
[
x
k
,
x
k
+
1
]
[x_{k},x_{k+1}]
[xk,xk+1] 上采用辛普森公式,若记
x
k
+
1
/
2
=
x
k
+
1
2
h
x_{k+1/2}=x_{k}+\frac{1}{2}h
xk+1/2=xk+21h ,则得
I
=
∫
a
b
f
(
x
)
d
x
=
∑
k
=
0
n
−
1
∫
x
k
x
k
+
1
f
(
x
)
d
x
=
h
6
∑
k
=
0
n
−
1
[
f
(
x
k
)
+
4
f
(
x
k
+
1
/
2
)
+
f
(
x
k
+
1
)
]
+
R
n
(
f
)
(
3.4
)
\begin{aligned} I &=\int_a^b f(x) \mathrm{d} x=\sum_{k=0}^{n-1} \int_{x_k}^{x_{k+1}} f(x) \mathrm{d} x \\ &=\frac{h}{6} \sum_{k=0}^{n-1}\left[f\left(x_k\right)+4 f\left(x_{k+1 / 2}\right)+f\left(x_{k+1}\right)\right]+R_n(f) \end{aligned} \quad\quad\quad (3.4)
I=∫abf(x)dx=k=0∑n−1∫xkxk+1f(x)dx=6hk=0∑n−1[f(xk)+4f(xk+1/2)+f(xk+1)]+Rn(f)(3.4)
记
S
n
=
h
6
∑
k
=
0
n
−
1
[
f
(
x
k
)
+
4
f
(
x
k
+
1
/
2
)
+
f
(
x
k
+
1
)
]
=
h
6
[
f
(
a
)
+
4
∑
k
=
0
n
−
1
f
(
x
k
+
1
/
2
)
+
2
∑
k
=
1
n
−
1
f
(
x
k
)
+
f
(
b
)
]
(
3.5
)
\begin{aligned} S_n &=\frac{h}{6} \sum_{k=0}^{n-1}\left[f\left(x_k\right)+4 f\left(x_{k+1 / 2}\right)+f\left(x_{k+1}\right)\right] \\ &=\frac{h}{6}\left[f(a)+4 \sum_{k=0}^{n-1} f\left(x_{k+1 / 2}\right)+2 \sum_{k=1}^{n-1} f\left(x_k\right)+f(b)\right] \end{aligned} \quad\quad\quad (3.5)
Sn=6hk=0∑n−1[f(xk)+4f(xk+1/2)+f(xk+1)]=6h[f(a)+4k=0∑n−1f(xk+1/2)+2k=1∑n−1f(xk)+f(b)](3.5)
称为复合辛普森求积公式。
(五)龙贝格求积公式
1.梯形法的递推化
复合求积方法可提高求积精度,实际计算时若精度不够可将步长逐次分半。设区间
[
a
,
b
]
[a,b]
[a,b] 分为
n
n
n 等分,共有
n
+
1
n+1
n+1 个分点,如果将求积区间再二分一次,则分点增至
2
n
+
1
2n+1
2n+1 个,将二分前后两个积分联系起来加以考察,注意到,每个子区间
[
x
k
,
x
k
+
1
]
[x_{k},x_{k+1}]
[xk,xk+1] 经过二分只增加了一个分点
x
k
+
1
2
=
1
2
(
x
k
+
x
k
+
1
)
x_{k+\frac{1}{2}}=\frac{1}{2}(x_{k}+x_{k+1})
xk+21=21(xk+xk+1) ,用复合梯形公式求得该子区间上的积分值为
h
4
[
f
(
x
k
)
+
2
f
(
x
k
+
1
2
)
+
f
(
x
k
+
1
)
]
\frac{h}{4}[f(x_{k})+2f(x_{k+\frac{1}{2}})+f(x_{k+1})]
4h[f(xk)+2f(xk+21)+f(xk+1)]
这里的
h
=
b
−
a
n
h=\frac{b-a}{n}
h=nb−a 代表二分前的步长,将每个子区间上的积分值相加得
T
2
n
=
h
4
∑
k
=
0
n
−
1
[
f
(
x
k
)
+
f
(
x
k
+
1
)
]
+
h
2
∑
k
=
0
n
−
1
f
(
x
k
+
1
2
)
T_{2 n}=\frac{h}{4} \sum_{k=0}^{n-1}\left[f\left(x_k\right)+f\left(x_{k+1}\right)\right]+\frac{h}{2} \sum_{k=0}^{n-1} f\left(x_{k+\frac{1}{2}}\right)
T2n=4hk=0∑n−1[f(xk)+f(xk+1)]+2hk=0∑n−1f(xk+21)
从而利用式
(
3.2
)
(3.2)
(3.2) 可导出下列递推公式:
T
2
n
=
1
2
T
n
+
h
2
∑
k
=
0
n
−
1
f
(
x
k
+
1
2
)
(
4.1
)
T_{2 n}=\frac{1}{2} T_n+\frac{h}{2} \sum_{k=0}^{n-1} f\left(x_{k+\frac{1}{2}}\right) \quad\quad\quad (4.1)
T2n=21Tn+2hk=0∑n−1f(xk+21)(4.1)
2.龙贝格算法
通过外推技巧,可得到统一形式的公式
T
m
(
h
)
=
4
m
4
m
−
1
T
m
−
1
(
h
2
)
−
1
4
m
−
1
T
m
−
1
(
h
)
(
4.9
)
T_m(h)=\frac{4^m}{4^m-1} T_{m-1}\left(\frac{h}{2}\right)-\frac{1}{4^m-1} T_{m-1}(h) \quad\quad\quad (4.9)
Tm(h)=4m−14mTm−1(2h)−4m−11Tm−1(h)(4.9)
上述处理方法通常称为理查森外推加速法。
设以
T
0
(
k
)
T_{0}^{(k)}
T0(k) 表示二分
k
k
k 次后求得的梯形值,且以
T
m
(
k
)
T_{m}^{(k)}
Tm(k) 表示序列
{
T
0
(
k
)
}
\{T_{0}^{(k)}\}
{T0(k)} 的
m
m
m 次加速值,则依递推公式
(
4.9
)
(4.9)
(4.9) 可得
T
m
(
k
)
=
4
m
4
m
−
1
T
m
−
1
(
k
+
1
)
−
1
4
m
−
1
T
m
−
1
(
k
)
,
k
=
1
,
2
,
⋯
(
4.11
)
T_m^{(k)}=\frac{4^m}{4^m-1} T_{m-1}^{(k+1)}-\frac{1}{4^m-1} T_{m-1}^{(k)}, \quad k=1,2, \cdots \quad\quad\quad (4.11)
Tm(k)=4m−14mTm−1(k+1)−4m−11Tm−1(k),k=1,2,⋯(4.11)
公式
(
4.11
)
(4.11)
(4.11) 也称为龙贝格算法,计算过程如下:
(1)取 k = 0 , h = b − a k=0,h=b-a k=0,h=b−a ,求 T 0 ( 0 ) = h 2 [ f ( a ) + f ( b ) ] T_{0}^{(0)}=\frac{h}{2}[f(a)+f(b)] T0(0)=2h[f(a)+f(b)] ,令 1 → k 1 \rightarrow k 1→k ( k k k 记区间 [ a , b ] [a,b] [a,b] 的二分次数)。
(2)求梯形值 T 0 ( b − a 2 k ) T_{0}(\frac{b-a}{2^{k}}) T0(2kb−a) ,即按递推公式 ( 4.1 ) (4.1) (4.1) 计算 T 0 ( k ) T_{0}^{(k)} T0(k) 。
(3)求加速值,按公式 ( 4.11 ) (4.11) (4.11) 逐个求出 T T T 表(表-2)的第 k k k 行其余各元素 T j ( k − j ) ( j = 1 , 2 , … , k ) T_{j}^{(k-j)}(j=1,2,\dots,k) Tj(k−j)(j=1,2,…,k) 。
(4)若 ∣ T k ( 0 ) − T k − 1 ( 0 ) ∣ < ε |T_{k}^{(0)}-T_{k-1}^{(0)}|<\varepsilon ∣Tk(0)−Tk−1(0)∣<ε(预先给定的精度),则终止计算,并取 T k 0 ≈ I T_{k}^{0} \approx I Tk0≈I ;否则令 k + 1 → k k+1 \rightarrow k k+1→k 转(2)继续计算。

(六)高斯求积公式
先研究带权积分
∫
a
b
f
(
x
)
ρ
(
x
)
d
x
\int_a^b f(x) \rho(x) dx
∫abf(x)ρ(x)dx ,这里的
ρ
(
x
)
\rho(x)
ρ(x) 为权函数,类似
(
1.3
)
(1.3)
(1.3) 式,它的求积公式为
∫
a
b
f
(
x
)
ρ
(
x
)
d
x
≈
∑
k
=
0
n
A
k
f
(
x
k
)
(
6.4
)
\int_a^b f(x) \rho(x) \mathrm{d} x \approx \sum_{k=0}^n A_k f\left(x_k\right) \quad\quad\quad (6.4)
∫abf(x)ρ(x)dx≈k=0∑nAkf(xk)(6.4)
A
k
(
k
=
0
,
1
,
…
,
n
)
A_{k}(k=0,1,\dots,n)
Ak(k=0,1,…,n) 为不依赖于
f
(
x
)
f(x)
f(x) 的求积系数,
x
k
(
k
=
0
,
1
,
…
,
n
)
x_{k}(k=0,1,\dots,n)
xk(k=0,1,…,n) 为求积节点,可适当选取
x
k
x_{k}
xk 以及
A
k
(
k
=
0
,
1
,
…
,
n
)
A_{k}(k=0,1,\dots,n)
Ak(k=0,1,…,n) 使
(
6.4
)
(6.4)
(6.4) 式具有
2
n
+
1
2n+1
2n+1 次代数精度。
如果求积公式 ( 6.4 ) (6.4) (6.4) 具有 2 n + 1 2n+1 2n+1 次代数精度,则称其节点 x k ( k = 0 , 1 , … , n ) x_{k}(k=0,1,\dots,n) xk(k=0,1,…,n) 为高斯点,相应公式 ( 6.4 ) (6.4) (6.4) 称为高斯型求积公式。
根据定义要使
(
6.4
)
(6.4)
(6.4) 式具有
2
n
+
1
2n+1
2n+1 次代数精度,只要取
f
(
x
)
=
x
m
f(x)=x^{m}
f(x)=xm ,对
m
=
0
,
1
,
…
,
2
n
+
1
m=0,1,\dots,2n+1
m=0,1,…,2n+1 ,
(
6.4
)
(6.4)
(6.4) 式精确成立,则得
∑
k
=
0
n
A
k
x
k
m
=
∫
a
b
x
m
ρ
(
x
)
d
x
m
=
0
,
1
,
⋯
,
2
n
+
1
(
6.5
)
\sum_{k=0}^n A_k x_k^m=\int_a^b x^m \rho(x) \mathrm{d} x \quad m=0,1, \cdots, 2 n+1 \quad\quad\quad (6.5)
k=0∑nAkxkm=∫abxmρ(x)dxm=0,1,⋯,2n+1(6.5)
当给定权函数
ρ
(
x
)
\rho(x)
ρ(x) ,求出右端积分,则可由
(
6.5
)
(6.5)
(6.5) 式解得
A
k
A_{k}
Ak 及
x
k
(
k
=
0
,
1
,
…
,
n
)
x_{k}(k=0,1,\dots,n)
xk(k=0,1,…,n) 。
1.高斯-勒让德求积公式
在高斯求积公式
(
6.4
)
(6.4)
(6.4) 中,若取权函数
ρ
(
x
)
=
1
\rho(x)=1
ρ(x)=1 ,区间为
[
−
1
,
1
]
[-1,1]
[−1,1] ,则得公式
∫
−
1
1
f
(
x
)
d
x
≈
∑
k
=
0
n
A
k
f
(
x
k
)
(
6.11
)
\int_{-1}^1 f(x) \mathrm{d} x \approx \sum_{k=0}^n A_k f\left(x_k\right) \quad\quad\quad (6.11)
∫−11f(x)dx≈k=0∑nAkf(xk)(6.11)
勒让德多项式是区间
[
−
1
,
1
]
[-1,1]
[−1,1] 上的正交多项式,因此,勒让德多项式
P
n
+
1
(
x
)
P_{n+1}(x)
Pn+1(x) 的零点就是求积公式
(
6.11
)
(6.11)
(6.11) 的高斯点,形如
(
6.11
)
(6.11)
(6.11) 式的高斯公式特别地称为高斯-勒让德求积公式。
若取
P
1
(
x
)
=
x
P_{1}(x)=x
P1(x)=x 的零点
x
0
=
0
x_0=0
x0=0 做节点构造求积公式
∫
−
1
1
f
(
x
)
d
x
≈
A
0
f
(
0
)
\int_{-1}^1 f(x) \mathrm{d} x \approx A_0 f(0)
∫−11f(x)dx≈A0f(0)
令它对
f
(
x
)
=
1
f(x)=1
f(x)=1 准确成立,即可定出
A
0
=
2
A_0=2
A0=2 。这样构造出的一点高斯-勒让德求积公式是中矩形公式。
再取
P
2
(
x
)
=
1
2
(
3
x
2
−
1
)
P_{2}(x)=\frac{1}{2}(3x^2-1)
P2(x)=21(3x2−1) 的两个零点
±
1
3
\pm \frac{1}{\sqrt{3}}
±31 构造求积公式
∫
−
1
1
f
(
x
)
d
x
≈
A
0
f
(
−
1
3
)
+
A
1
f
(
1
3
)
\int_{-1}^1 f(x) \mathrm{d} x \approx A_0 f\left(-\frac{1}{\sqrt{3}}\right)+A_1 f\left(\frac{1}{\sqrt{3}}\right)
∫−11f(x)dx≈A0f(−31)+A1f(31)
在先验知识中已知
A
0
=
A
1
=
1
A_0=A_1=1
A0=A1=1 ,因此求积公式为
∫
−
1
1
f
(
x
)
d
x
≈
f
(
−
1
3
)
+
f
(
1
3
)
\int_{-1}^1 f(x) \mathrm{d} x \approx f\left(-\frac{1}{\sqrt{3}}\right)+f\left(\frac{1}{\sqrt{3}}\right)
∫−11f(x)dx≈f(−31)+f(31)
三点高斯-勒让德公式的形式是
∫
−
1
1
f
(
x
)
d
x
≈
5
9
f
(
−
15
5
)
+
8
9
f
(
0
)
+
5
9
f
(
15
5
)
\int_{-1}^1 f(x) \mathrm{d} x \approx \frac{5}{9} f\left(-\frac{\sqrt{15}}{5}\right)+\frac{8}{9} f(0)+\frac{5}{9} f\left(\frac{\sqrt{15}}{5}\right)
∫−11f(x)dx≈95f(−515)+98f(0)+95f(515)
表-3 列出高斯-勒让德求积公式
(
6.11
)
(6.11)
(6.11) 的节点和系数。
| n n n | x k x_{k} xk | A k A_{k} Ak |
|---|---|---|
| 0 | 0.0000000 | 2.0000000 |
| 1 | ±0.5773503 | 1.0000000 |
| 2 | ±0.7745967 0.0000000 | 0.5555556 0.8888889 |
| 3 | ±0.8611363 ±0.3399810 | 0.3478548 0.6521452 |
| 4 | ±0.9061798 ±0.5384693 0.0000000 | 0.2369269 0.4786287 0.5688889 |
| 5 | ±0.9324695 ±0.6612094 ±0.2386192 | 0.1713245 0.3607616 0.4679139 |
当积分区间不是
[
−
1
,
1
]
[-1,1]
[−1,1] ,而是一般的区间
[
a
,
b
]
[a,b]
[a,b] 时,只要做变换
x
=
b
−
a
2
t
+
a
+
b
2
x=\frac{b-a}{2} t+\frac{a+b}{2}
x=2b−at+2a+b
可将
[
a
,
b
]
[a,b]
[a,b] 化为
[
−
1
,
1
]
[-1,1]
[−1,1] ,这时
∫
a
b
f
(
x
)
d
x
=
b
−
a
2
∫
−
1
1
f
(
b
−
a
2
t
+
a
+
b
2
)
d
t
(
6.13
)
\int_a^b f(x) \mathrm{d} x=\frac{b-a}{2} \int_{-1}^1 f\left(\frac{b-a}{2} t+\frac{a+b}{2}\right) \mathrm{d} t \quad\quad\quad (6.13)
∫abf(x)dx=2b−a∫−11f(2b−at+2a+b)dt(6.13)
对等式右端的积分即可使用高斯-勒让德求积公式。
四、实验步骤

(一)求解积分的设定
先定义积分:
I
=
∫
0
1
x
ln
x
d
x
=
−
4
9
I=\int_0^1 \sqrt{x} \ln x \mathrm{~d} x=-\frac{4}{9}
I=∫01xlnx dx=−94
在此前提下实现下面的步骤。
(二)不同方法的实现
1.梯形公式与矩形公式
(1)编写程序实现基本的梯形公式以及矩形公式。
(2)利用梯形公式和矩形公式分别计算积分 I I I 。
(3)输出结果与真实值对比。
2.辛普森公式和科特斯公式
(1)编写程序实现辛普森公式以及科特斯公式。
(2)利用辛普森公式和科特斯公式分别计算积分 I I I 。
(3)输出结果与真实值对比。
3.复合求积公式
(1)编写程序实现复合梯形公式、复合辛普森方式以及复合科特斯公式。
(2)分别将区间 [ 0 , 1 ] [0,1] [0,1] 分成 n = 2 k ( k = 3 , 4 , … , 10 ) n=2^{k}(k=3,4,\dots,10) n=2k(k=3,4,…,10) 等份,分别利用复合梯形公式、复合辛普森公式和复合科特斯公式计算积分 I I I 。
(3)输出结果与真实值对比。
4.龙贝格算法及其改进
(1)编写程序实现龙贝格算法。
(2)分别取 k = 5 , 8 , 12 , 20 k=5,8,12,20 k=5,8,12,20 ,利用龙贝格算法计算积分 I I I。
(3)输出结果并与真实值对比。
(4)基于对龙贝格算法原理的理解,尝试提出改进——将原本基于梯形公式的外推加速法改为基于辛普森公式的外推加速法,最终得出改进后的龙贝格算法。
(5)分别取 k = 5 , 8 , 12 k=5,8,12 k=5,8,12 ,利用改进后的龙贝格算法计算积分 I I I 。
(6)输出结果,与真实值以及与原本的龙贝格算法进行对比,观察是否能得到更加快速的收敛效果。
5.高斯-勒让德求积公式
(1)编写程序分别实现三点高斯-勒让德求积公式、六点高斯-勒让德求积公式。
(2)分别利用三点高斯-勒让德求积公式以及六点高斯-勒让德求积公式计算积分 I I I 。
(3)输出结果,并与真实值对比。
五、实验结果
(一)各方法的运行结果
1.梯形公式
(1)运行结果

(2)与真实值对比
| 梯形公式结果 | 真实值 |
|---|---|
| 0.0 | 0.44444… |
2.矩形公式
(1)运行结果

(2)与真实值对比
| 矩形公式结果 | 真实值 |
|---|---|
| -0.49012 | -0.44444… |
3.辛普森公式
(1)运行结果

(2)与真实值对比
| 辛普森公式结果 | 真实值 |
|---|---|
| -0.32675 | -0.44444… |
4.科特斯公式
(1)运行结果

(2)与真实值对比
| 科特斯公式结果 | 真实值 |
|---|---|
| -0.40038 | -0.44444… |
5.复合梯形公式
(1)运行结果

(2)与真实值对比
| n n n | 复合梯形公式结果 | 真实值 |
|---|---|---|
| 8 | -0.40809 | -0.44444… |
| 16 | -0.42947 | -0.44444… |
| 32 | -0.43838 | -0.44444… |
| 64 | -0.44203 | -0.44444… |
| 128 | -0.44349 | -0.44444… |
| 256 | -0.44407 | -0.44444… |
| 512 | -0.44430 | -0.44444… |
| 1024 | -0.44438 | -0.44444… |
由此可见,当复合梯形公式的 n n n 越大,即将区间 [ 0 , 1 ] [0,1] [0,1] 划分得越细,得到的结果越接近真实值。
6.复合辛普森公式
(1)运行结果

(2)与真实值对比
| n n n | 复合辛普森公式结果 | 真实值 |
|---|---|---|
| 8 | -0.43660 | -0.44444… |
| 16 | -0.44136 | -0.44444… |
| 32 | -0.44324 | -0.44444… |
| 64 | -0.44398 | -0.44444… |
| 128 | -0.44426 | -0.44444… |
| 256 | -0.44437 | -0.44444… |
| 512 | -0.44441 | -0.44444… |
| 1024 | -0.44443 | -0.44444… |
由此可见,当复合辛普森公式的 n n n 越大,即将区间 [ 0 , 1 ] [0,1] [0,1] 划分得越细,得到的结果越接近真实值,且收敛速度比复合梯形公式更快。
7.复合科特斯公式
(1)运行结果

(2)与真实值对比
| n n n | 复合科特斯公式结果 | 真实值 |
|---|---|---|
| 8 | -0.441678 | -0.44444… |
| 16 | -0.443369 | -0.44444… |
| 32 | -0.444030 | -0.44444… |
| 64 | -0.444286 | -0.44444… |
| 128 | -0.444384 | -0.44444… |
| 256 | -0.444421 | -0.44444… |
| 512 | -0.444435 | -0.44444… |
| 1024 | -0.444441 | -0.44444… |
由此可见,当复合科特斯公式的 n n n 越大,即将区间 [ 0 , 1 ] [0,1] [0,1] 划分得越细,得到的结果越接近真实值,且收敛速度比复合梯形公式和复合辛普森公式都要快。
8.龙贝格算法
(1)运行结果

| k k k | T 0 ( k ) T_{0}^{(k)} T0(k) | T 1 ( k ) T_{1}^{(k)} T1(k) | T 2 ( k ) T_{2}^{(k)} T2(k) | T 3 ( k ) T_{3}^{(k)} T3(k) | T 4 ( k ) T_{4}^{(k)} T4(k) | T 5 ( k ) T_{5}^{(k)} T5(k) |
|---|---|---|---|---|---|---|
| 0 | 0.0 | |||||
| 1 | -0.24506 | -0.32675 | ||||
| 2 | -0.35810 | -0.39578 | -0.40038 | |||
| 3 | -0.40809 | -0.42475 | -0.42668 | -0.42710 | ||
| 4 | -0.42947 | -0.43660 | -0.43739 | -0.43756 | -0.43760 | |
| 5 | -0.43838 | -0.44136 | -0.44167 | -0.44174 | -0.44176 | -0.44176 |
(由于篇幅有限,这里只给到 k = 5 k=5 k=5 的计算结果T表)
(2)与真实值对比
| k k k | 龙贝格算法计算结果 | 真实值 |
|---|---|---|
| 5 | -0.441766839 | -0.444444… |
| 8 | -0.444291362 | -0.444444… |
| 12 | -0.444441327 | -0.444444… |
| 20 | -0.444444443 | -0.444444… |
当 k k k 值越大,龙贝格算法的精确度越高,且可以观察到,当 k = 20 k=20 k=20 时,精确度已经可以到达 1 0 − 8 10^{-8} 10−8 。
9.改进后的龙贝格算法
(1)运行结果

| k k k | T 0 ( k ) T_{0}^{(k)} T0(k) | T 1 ( k ) T_{1}^{(k)} T1(k) | T 2 ( k ) T_{2}^{(k)} T2(k) | T 3 ( k ) T_{3}^{(k)} T3(k) | T 4 ( k ) T_{4}^{(k)} T4(k) | T 5 ( k ) T_{5}^{(k)} T5(k) |
|---|---|---|---|---|---|---|
| 0 | -0.32675 | |||||
| 1 | -0.39578 | -0.41879 | ||||
| 2 | -0.42475 | -0.43440 | -0.43544 | |||
| 3 | -0.43660 | -0.44055 | -0.44096 | -0.44105 | ||
| 4 | -0.44136 | -0.44294 | -0.44310 | -0.44314 | -0.44314 | |
| 5 | -0.44324 | -0.44387 | -0.44393 | -0.44394 | -0.44395 | -0.44395 |
(由于篇幅有限,这里只给到 k = 5 k=5 k=5 的计算结果T表)可以看出,改进后的龙贝格算法:
- 不仅解决了原本算法 k = 0 k=0 k=0 时得到结果为 0 ,与真实值有巨大偏差的问题;
- 同时,在 k k k 取相同的值时,改进后的龙贝格算法收敛的速度也比原本的龙贝格算法更加迅速,得到了较为可观的提升。
(2)与真实值对比
| k k k | 改进后的龙贝格算法计算结果 | 真实值 |
|---|---|---|
| 5 | -0.443950 | -0.444444… |
| 8 | -0.444417 | -0.444444… |
| 12 | -0.444443 | -0.444444… |
10.三点高斯-勒让德求积公式
(1)运行结果

(2)与真实值对比
| 三点高斯-勒让德求积公式结果 | 真实值 |
|---|---|
| -0.45269 | -0.44444… |
11.六点高斯-勒让德求积公式
(1)运行结果

(2)与真实值对比
| 六点高斯-勒让德求积公式结果 | 真实值 |
|---|---|
| -0.44618 | -0.44444… |
(二)各类方法运行结果汇总
| 数值积分方法 | 运行结果 | 函数积分真实值 |
|---|---|---|
| 梯形公式 | 0.0 | -0.44444… |
| 矩形公式 | -0.49012 | -0.44444… |
| 辛普森公式 | -0.32675 | -0.44444… |
| 科特斯公式 | -0.40038 | -0.44444… |
| n = 8 n=8 n=8 的复合梯形公式 | -0.40809 | -0.44444… |
| n = 128 n=128 n=128 的复合梯形公式 | -0.44349 | -0.44444… |
| n = 1024 n=1024 n=1024 的复合梯形公式 | -0.44438 | -0.44444… |
| n = 8 n=8 n=8 的复合辛普森公式 | -0.43660 | -0.44444… |
| n = 128 n=128 n=128 的复合辛普森公式 | -0.44426 | -0.44444… |
| n = 1024 n=1024 n=1024 的复合辛普森公式 | -0.44443 | -0.44444… |
| n = 8 n=8 n=8 的复合科特斯公式 | -0.441678 | -0.44444… |
| n = 128 n=128 n=128 的复合科特斯公式 | -0.444384 | -0.44444… |
| n = 1024 n=1024 n=1024 的复合科特斯公式 | -0.444441 | -0.44444… |
| k = 5 k=5 k=5 的龙贝格算法 | -0.441766839 | -0.44444… |
| k = 20 k=20 k=20 的龙贝格算法 | -0.444444443 | -0.44444… |
| k = 5 k=5 k=5 的改进版龙贝格算法 | -0.443950 | -0.44444… |
| k = 12 k=12 k=12 的改进版龙贝格算法 | -0.444443 | -0.44444… |
| 三点高斯-勒让德求积公式 | -0.45269 | -0.44444… |
| 六点高斯-勒让德求积公式 | -0.44618 | -0.44444… |
六、代码
(代码按照从上到下的顺序即可运行)
# 定义函数
import numpy as np
# 积分上下限
a = 0
b = 1
def func(x):
if x == 0:
result = 0
else:
result = np.sqrt(x) * np.log(x)
return result
# 真实积分值
real_value = -4 / 9
print(f"真实的积分值为:{real_value}")
# 梯形公式
def trapezoid_formula(a, b):
result = (b - a) * (func(a) + func(b)) / 2
return result
print(f"梯形公式的结果为:{trapezoid_formula(a, b)}")
# 矩形公式
def rectangular_formula(a, b):
result = (b - a) * func((a + b) / 2)
return result
print(f"矩形公式的结果为:{rectangular_formula(a, b)}")
# 辛普森公式
def simpson_formula(a, b):
result = (b - a) * (func(a) + 4 * func((a + b) / 2) + func(b)) / 6
return result
print(f"辛普森公式的结果为:{simpson_formula(a, b)}")
# 科特斯公式
def cotes_formula(a, b):
h = (b - a) / 4
coefficient_list = [7, 32, 12, 32, 7]
C = 0
for k in range(len(coefficient_list)):
C = C + coefficient_list[k] * func(a + k * h)
C = C * (b - a) / 90
return C
print(f"科特斯公式的结果为:{cotes_formula(a, b)}")
# 复合梯形公式
def compound_trapezoidal_formula(a, b, n):
h = (b - a) / n
result = 0
for k in range(n + 1):
x_k = a + k * h
if k == 0 or k == n:
result = result + func(x_k)
else:
result = result + 2 * func(x_k)
result = result * h / 2
return result
n_list = [8, 16, 32, 64, 128, 256, 512, 1024]
for n in n_list:
print(f"将区间分为{n}等份时,复合梯形公式的结果为:{compound_trapezoidal_formula(a, b, n)}")
# 复合辛普森公式
def compound_simpson_formula(a, b, n):
h = (b - a) / n
result = 0
for k in range(n):
x_k = a + k * h
x_k_h = x_k + h / 2
x_k_p = a + (k + 1) * h
result = result + func(x_k) + 4 * func(x_k_h) + func(x_k_p)
result = result * h / 6
return result
n_list = [8, 16, 32, 64, 128, 256, 512, 1024]
for n in n_list:
print(f"将区间分为{n}等份时,复合辛普森公式的结果为:{compound_simpson_formula(a, b, n)}")
# 复合科特斯公式
def compound_cotes_formula(a, b, n):
h = (b - a) / n
result = 0
for k in range(n):
x0 = a + k * h
x1 = x0 + h / 4
x2 = x0 + h / 2
x3 = x0 + h * 3 / 4
x4 = a + (k + 1) * h
result = result + 7 * (func(x0) + func(x4)) + 32 * (func(x1) + func(x3)) + 12 * func(x2)
result = result * h / 90
return result
n_list = [8, 16, 32, 64, 128, 256, 512, 1024]
for n in n_list:
print(f"将区间分为{n}等份时,复合科特斯公式的结果为:{compound_cotes_formula(a, b, n)}")
# 龙贝格算法
def Lomberg_algorithm(a, b, k):
T = np.zeros((k, k))
T[0][0] = compound_trapezoidal_formula(a, b, 1)
for i in range(1, k):
for j in range(i + 1):
if j == 0:
T[i][j] = compound_trapezoidal_formula(a, b, 2 ** i)
else:
T[i][j] = 4 ** j * T[i][j - 1] / (4 ** j - 1) - T[i - 1][j - 1] / (4 ** j - 1)
return T
k_list = [5, 8, 12, 20]
for k in k_list:
if k == 5:
print(f"当龙贝格算法 k = {k} 时, 计算结果表为:\n{Lomberg_algorithm(a, b, k + 1)}")
print(f"当 k = {k} 时,计算结果为:{Lomberg_algorithm(a, b, k + 1)[k][k]}")
# 改进后的龙贝格算法
def promoted_Lomberg_algorithm(a, b, k):
T = np.zeros((k, k))
T[0][0] = compound_simpson_formula(a, b, 1)
for i in range(1, k):
for j in range(i + 1):
if j == 0:
T[i][j] = compound_simpson_formula(a, b, 2 ** i)
else:
T[i][j] = 4 ** j * T[i][j - 1] / (4 ** j - 1) - T[i - 1][j - 1] / (4 ** j - 1)
return T
k_list = [5, 8, 12]
for k in k_list:
if k == 5:
print(f"当改进后的龙贝格算法 k = {k} 时, 计算结果表为:\n{promoted_Lomberg_algorithm(a, b, k + 1)}")
print(f"当 k = {k} 时,计算结果为:{promoted_Lomberg_algorithm(a, b, k + 1)[k][k]}")
# 三点-高斯勒让德求积公式
def transform_segment(a, b, t):
x = ((b - a) * t + (a + b)) / 2
return x
def three_point_Gauss(a, b):
x0 = transform_segment(a, b, -0.7745967)
x1 = transform_segment(a, b, 0.0)
x2 = transform_segment(a, b, 0.7745967)
result = (5 * func(x0) + 8 * func(x1) + 5 * func(x2)) / 9
result = (b - a) * result / 2
return result
print(f"三点高斯-勒让德求积公式的结果为:{three_point_Gauss(a, b)}")
# 六点-高斯勒让德求积公式
def six_point_Gauss(a, b):
x0 = transform_segment(a, b, -0.9324695)
x1 = transform_segment(a, b, -0.6612094)
x2 = transform_segment(a, b, -0.2386192)
x3 = transform_segment(a, b, 0.2386192)
x4 = transform_segment(a, b, 0.6612094)
x5 = transform_segment(a, b, 0.9324695)
result = 0.1713245 * (func(x0) + func(x5)) + 0.3607616 * (func(x1) + func(x4)) + 0.4679139 * (func(x2) + func(x3))
result = (b - a) * result / 2
return result
print(f"六点高斯-勒让德求积公式的结果为:{six_point_Gauss(a, b)}")
``





















 372
372











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








