（五）分类算法——决策树

1.算法概念

决策树，将大量的样本通过每一次分支后，将数据进行分类，（算是个分类模型，让数据按类别进行筛选）而分支上的条件是利用一定的训练样本，从数据中“学习”出决策规则，自动构造出决策树。比如下方的例子。

在学习决策树之前， 我们需要先知道几个概念。

信息熵、条件熵、信息增益、基尼系数、还有信息增益率

具体可以参照这篇文章：决策树模型及案例（Python）

根据上面的几个概念，我们根据划分标准的不同，衍生出了三种决策方法。

具体使用哪个方法，要根据使用场景、样本数量、样本特征等情况进行分析和选择。

具体可以参考这篇文章：决策树分类

2.算法流程

下面我们来说一下ID3的基本流程：

①计算当前节点包含的所有样本的信息熵

②比较采用不同特征值进行分枝得到的信息增益（就是说怎么分类才能让混乱程度减小的多）

③选取具有最大信息增益的特征赋予当前节点（选让混乱程度减小最多的节点作为当前节点）

④构造决策树的下一层节点，需要分别考察两组样本上采用不同特征所得到的信息增益，采用较大信息增益的特征构建下一层

⑤若后续节点只包含一类样本，停止该枝生长；若还包含不同类样本，再重复以上步骤

举个栗子：

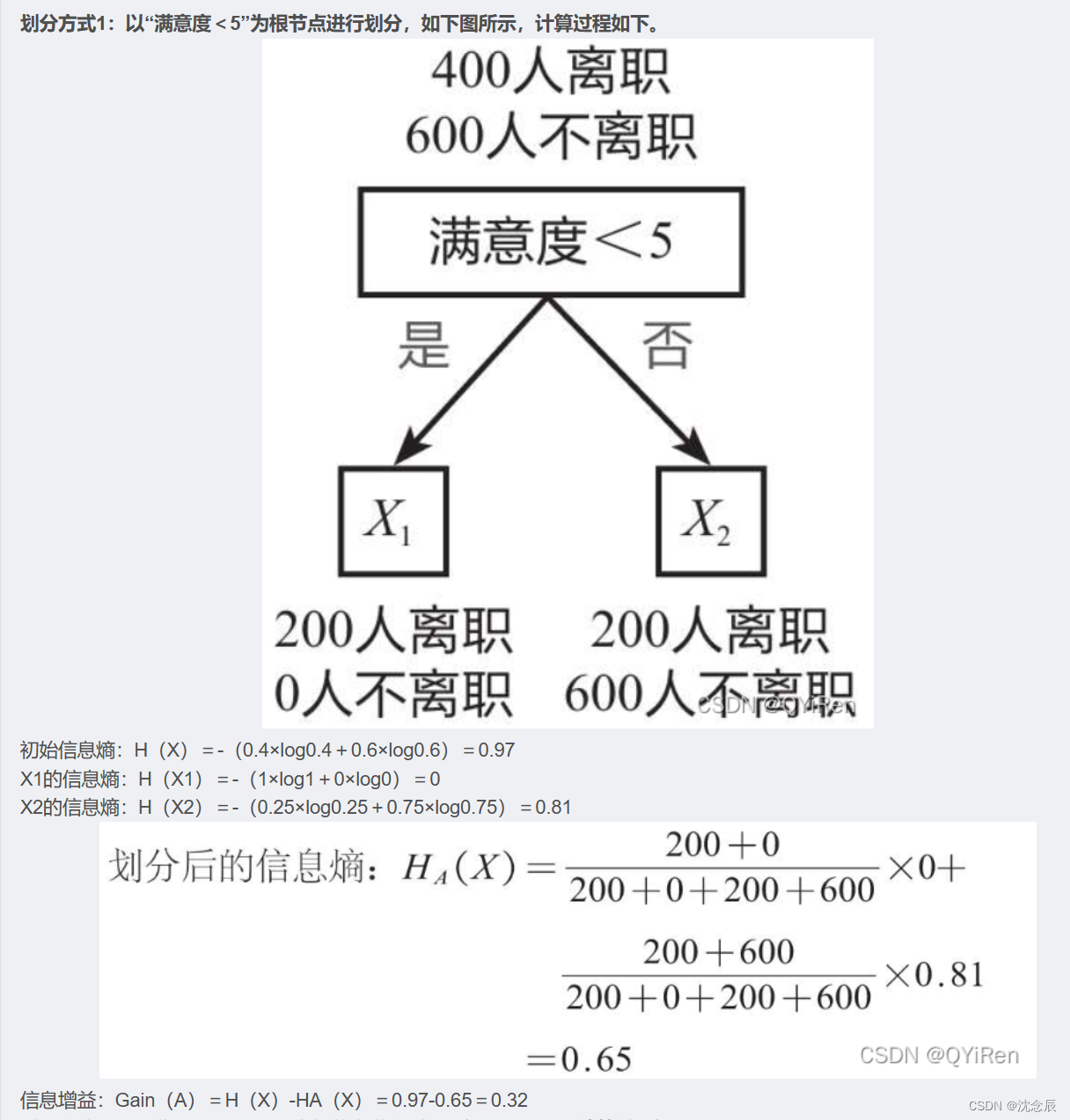
用满意度作为节点信息增益为0.32（也就是说让混乱度下降了，越分类数据越清晰）

用收入作为节点，信息增益为0.046，也就说明用满意度作为节点更好，因为他能更好的让混乱度下降。

当然我们还可以整体的去理解一下决策树的构建。

1） 开始：构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。

2） 如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。

3）如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。

4）每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树。

3.算法应用

ID3使用信息增益偏向特征值多的特征，且只能用于分类问题，

4.算法优缺点

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据

缺点：可能会产生过度匹配的问题，ID3算法过慢、没有剪枝策略、只能处理离散数据且缺失值敏感

5.算法代码

clear;

% 西瓜数据集
data=["青绿","蜷缩","浊响","清晰","凹陷","硬滑","是";
    "乌黑","蜷缩","沉闷","清晰","凹陷","硬滑","是";
    "乌黑","蜷缩","浊响","清晰","凹陷","硬滑","是";
    "青绿","蜷缩","沉闷","清晰","凹陷","硬滑","是";
    "浅白","蜷缩","浊响","清晰","凹陷","硬滑","是";
    "青绿","稍蜷","浊响","清晰","稍凹","软粘","是";
    "乌黑","稍蜷","浊响","稍糊","稍凹","软粘","是";
    "乌黑","稍蜷","浊响","清晰","稍凹","硬滑","是";
    "乌黑","稍蜷","沉闷","稍糊","稍凹","硬滑","否";
    "青绿","硬挺","清脆","清晰","平坦","软粘","否";
    "浅白","硬挺","清脆","模糊","平坦","硬滑","否";
    "浅白","蜷缩","浊响","模糊","平坦","软粘","否";
    "青绿","稍蜷","浊响","稍糊","凹陷","硬滑","否";
    "浅白","稍蜷","沉闷","稍糊","凹陷","硬滑","否";
    "乌黑","稍蜷","浊响","清晰","稍凹","软粘","否";
    "浅白","蜷缩","浊响","模糊","平坦","硬滑","否";
    "青绿","蜷缩","沉闷","稍糊","稍凹","硬滑","否"];

label = ["色泽","根蒂","敲声","纹理","脐部","触感","好瓜"];

% 参数预定义
datasetRate = 1;
dataSize = size(data);

% 数据预处理
index = randperm(17,round(datasetRate*(dataSize(1,1)-1)));
trainSet = data(index,:);
testSet = data;
testSet(index,:) = [];

% 所有标签
deepth = ones(1,dataSize(1,2)-1);
% 生成树
rootNode = makeTree(label,trainSet,deepth,'null');
% 画出决策树
drawTree(rootNode);

% 计算熵不纯度
function res = calculateImpurity(examples_)
    P1 = 0;
    P2 = 0;
    [m_,n_] = size(examples_);
    P1 = sum(examples_(:,n_) == '是');
    P2 = sum(examples_(:,n_) == '否');
    P1 = P1 / m_;
    P2 = P2 / m_;
    if P1 == 1 || P1 == 0
        res = 0;
    else
        res = -(P1*log2(P1)+P2*log2(P2));
    end
end

% 决策过程 获取信息增量最大的分类标准
function label = getBestlabel(impurity_,features_,samples_)
    % impurity_:划分前的熵不纯度
    % features_:当前可供分类的标签 是01矩阵
    % samples_:当前需要分类的样本
    [m,n]=size(samples_);
    delta_impurity = zeros(1,n-1);
    
    % 遍历每个特征 每个特征把m个样本分为t组 每组m_t个样本 计算每个特征的不纯度减少量delta_impurity(i)
    % 输入样本为m行n列矩阵 特征总数量为n-1
    
    for i = 1:n-1
        % 存放分类结果
        count = 1;
        grouping_res = strings;
        sample_nums = [];
        grouped_impurity = [];% 分类结果按分组计算熵不纯度
        grouped_P = [];
        % 如果features_(i)为1 说明该分支上该标签还未用于分类
        if features_(i) == 1
            % 分组
            for j = 1:m
                pos = grouping_res == samples_(j,i);
                if sum(pos)
                    % 分类样本 计算同一标签类别的样本数量
                    sample_nums(pos) = sample_nums(pos) + 1;
                else   
                    % 将标签的类别添加到统计结果
                    sample_nums = [sample_nums 1];
                    grouping_res(count) = samples_(j,i);
                    count = count + 1;
                end
            end
            % 计算该分类结果的不纯度减少量
            % 按分组计算熵不纯度
            for k = grouping_res
                sub_sample = samples_(samples_(:,i)==k,:);
                grouped_impurity = [grouped_impurity calculateImpurity(sub_sample)];
                grouped_P = [grouped_P sum(sub_sample(:,n)=='是')/sum(samples_(:,i)==k)];
            end
            delta_impurity(i) = impurity_ - sum(grouped_P.*grouped_impurity);
        end
    end
    % 返回的label是索引数组
    temp = delta_impurity==max(delta_impurity);
    % 如果存在多个结果一样的标签 则使用第一个
    label = find(temp,1);
end

% 生成决策树
function node = makeTree(features,examples,deepth,branch)
    % feature:样本分类依据的所有标签
    % examples:样本
    % deepth:树的深度，每被分类一次与分类标签对应的值置零

    % value:分类结果，若为null则表示该节点是分支节点
    % label:节点划分标签
    % branch:分支值
    % children:子节点
    node = struct('value','null','label',[],'branch',branch,'children',[]);
    
    [m,n] = size(examples);
    sample = examples(1,n);
    check_res = true;
    for i = 1:m
        if sample ~= examples(i,n)
            check_res = false;
        end
    end
    % 若样本中全为同一分类结果 则作为叶节点
    if check_res
        node.value = examples(1,n);
        return;
    end
    
    % 计算熵不纯度
    impurity = calculateImpurity(examples);
    % 选择合适的标签
    bestLabel = getBestlabel(impurity,deepth,examples);
    deepth(bestLabel) = 0;
    node.label = features(bestLabel);
    
    % 分类
    grouping_res = strings;
    count = 1;
    for i = 1:m
        pos = grouping_res == examples(i,bestLabel);
        if sum(pos)
            % 分类样本 计算同一标签类别的样本数量
        else   
            % 将标签的类别添加到统计结果
            grouping_res(count) = examples(i,bestLabel);
            count = count + 1;
        end
    end
    
    for k = grouping_res
        sub_sample = examples(examples(:,bestLabel)==k,:);
        node.children = [node.children makeTree(features,sub_sample,deepth,k)];
    end
    
end

% 画出决策树
function [] = drawTree(node)
    % 遍历树
    nodeVec = [];
    nodeSpec = [];
    edgeSpec = [];
    [nodeVec,nodeSpec,edgeSpec,total] = travesing(node,0,0,nodeVec,nodeSpec,edgeSpec);
    treeplot(nodeVec);
    [x,y] = treelayout(nodeVec);
    [m,n] = size(nodeVec);
    x = x';
    y = y';
    text(x(:,1),y(:,1),nodeSpec,'VerticalAlignment','bottom','HorizontalAlignment','right');
    x_branch = [];
    y_branch = [];
    for i = 2:n
        x_branch = [x_branch; (x(i,1)+x(nodeVec(i),1))/2];
        y_branch = [y_branch; (y(i,1)+y(nodeVec(i),1))/2];
    end
    text(x_branch(:,1),y_branch(:,1),edgeSpec(1,2:n),'VerticalAlignment','bottom','HorizontalAlignment','right');
end

% 遍历树
function [nodeVec,nodeSpec,edgeSpec,current_count] = travesing(node,current_count,last_node,nodeVec,nodeSpec,edgeSpec)
    nodeVec = [nodeVec last_node];
    if node.value == 'null'
        nodeSpec = [nodeSpec node.label];
    else
        if node.value == '是'
            nodeSpec = [nodeSpec '好瓜'];
        else
            nodeSpec = [nodeSpec '坏瓜'];
        end
    end
    edgeSpec = [edgeSpec node.branch];
    current_count = current_count + 1;
    current_node = current_count;
    if node.value ~= 'null'
        return;
    end
    for next_ndoe = node.children
        [nodeVec,nodeSpec,edgeSpec,current_count] = travesing(next_ndoe,current_count,current_node,nodeVec,nodeSpec,edgeSpec);
    end
end