@[TOC](Potions (Hard Version) and (Easy Version))
一、Potions(Easy Version)
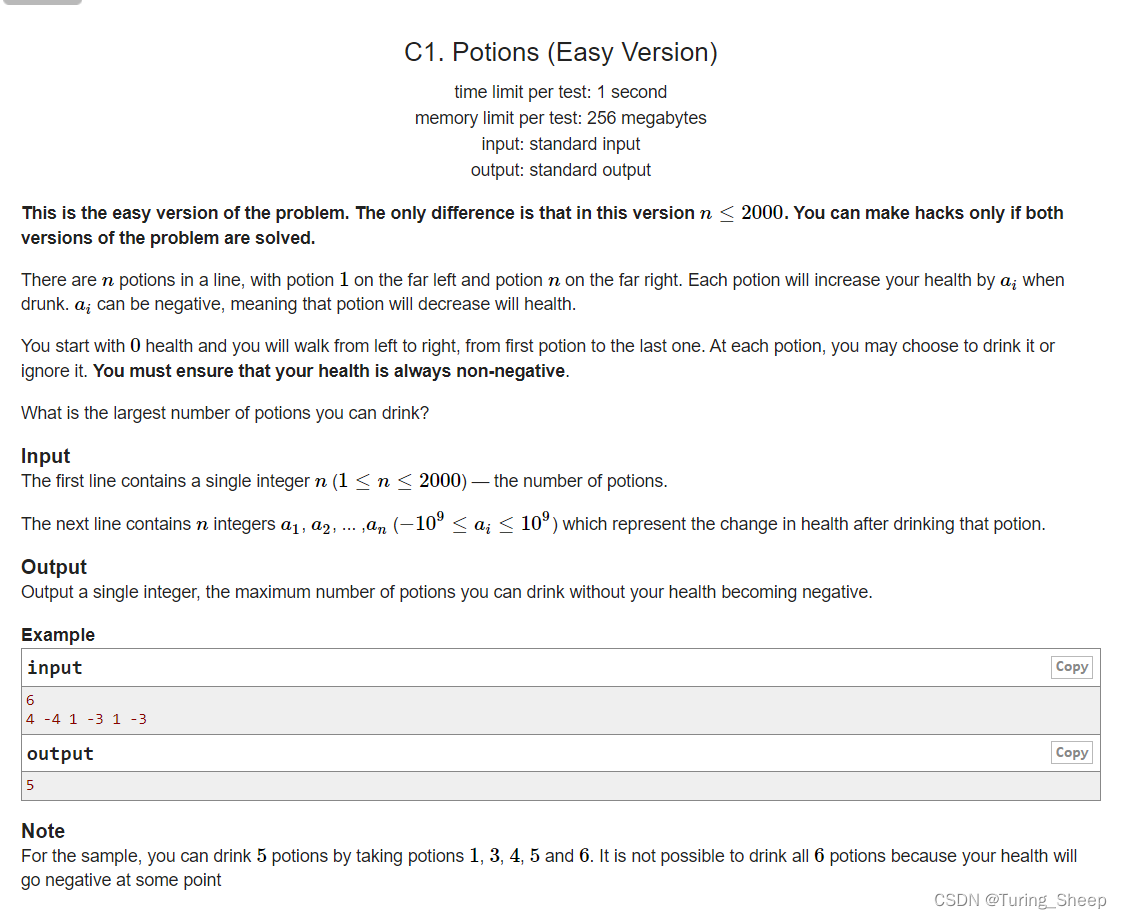
1、问题
2、分析(背包DP + 贪心)
简而言之就是我们需要从左到右开始选数字,选的过程中我们需要保证我们选的数字的和始终是大于等于0的,在满足这个条件的情况下求出我们所选的数字的个数的最大值。
由于这个简单版本的数据范围是2000,还是比较小的,所以我们可以使用 O ( n 2 ) O(n^2) O(n2)的DP来解决。
假设我们的DP数组是: f [ i ] [ j ] f[i][j] f[i][j]
这里的一个难点就是这个数组的含义是什么?
我们这里的定义是:在前 i i i个数字里面选,恰好选择 j j j个数字时,数字之和的最大值。
我们先来解释一下,为什么我们要存储最大值。
假设我们在前 i i i个物品里选择了 j j j个,那么这 j j j个数字的和越大,我们后续的选择空间越大,这是一种贪心的想法。
那么我们如何求出最后的结果呢?
根据题目要求,我们的 f [ i ] [ j ] ≥ 0 f[i][j]\geq 0 f[i][j]≥0。
所以我们可以去遍历 f [ n ] [ i ] f[n][i] f[n][i],只要这个数大于等于0,我们就可以让我们的 a n s = i ans = i ans=i。最后一个大于等于0的 f [ n ] [ i ] f[n][i] f[n][i]所对应的 i i i就是我们的答案。
转移方程:
f
[
i
]
[
j
]
=
{
f
[
i
−
1
]
[
j
]
m
a
x
(
f
[
i
−
1
]
[
j
−
1
]
+
a
[
i
]
,
f
[
i
−
1
]
[
j
]
)
f
[
i
−
1
]
[
j
−
1
]
≥
0
f[i][j] = \begin{cases} f[i - 1][j]\\ max\bigg(f[i - 1][j - 1] + a[i], f[i -1][j]\bigg)&f[i- 1][j- 1]\geq 0 \end{cases}
f[i][j]=⎩
⎨
⎧f[i−1][j]max(f[i−1][j−1]+a[i],f[i−1][j])f[i−1][j−1]≥0
因为只有在当前数字的和大于等于0的时候,我们才能去选下一个。所以我们需要让
f
[
i
−
1
]
[
j
−
1
]
f[i-1][j-1]
f[i−1][j−1]大于0。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2010;
ll a[N], f[N][N];
void solve()
{
int n;
cin >> n;
for(int i = 1; i <= n; i ++ )
cin >> a[i];
memset(f, 0xcf, sizeof f);
f[0][0] = 0;
for(int i = 1; i <= n; i ++ )
{
for(int j = 0; j <= i; j ++ )
{
f[i][j] = f[i - 1][j];
if(j >= 1 && f[i - 1][j - 1] >= 0)
f[i][j] = max(f[i - 1][j - 1] + a[i], f[i][j]);
}
}
int ans = 0;
for(int i = 0; i <= n; i ++ )
{
if(f[n][i] >= 0)
ans = i;
}
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
}
二、Potions(Hard Version)
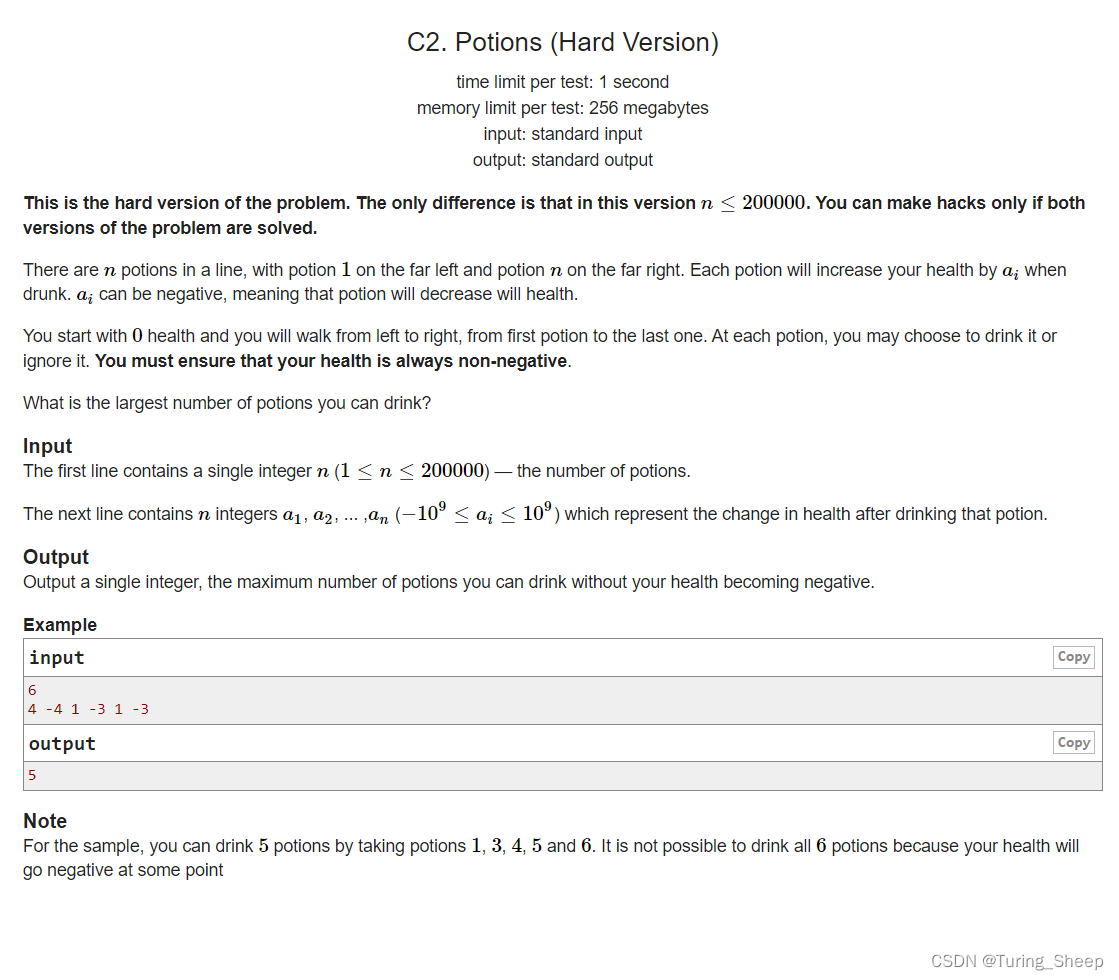
1、问题
2、分析(反悔贪心)
这道题和上一道题的唯一区别就是我们的数据范围变得很大,所以二维DP数组是存储不下的,即使我们逆序遍历从而优化掉一维的话,我们的时间复杂度也是平方级别的,依然过不了。
因此,我们就只能想别的方法了。
这里采用的也是贪心策略。
我们从左到右开始枚举每一个数,在枚举的过程中我们会发现,正数一定是要选择的,所以遇到正数我们就加上即可。
这里的重点是负数的选择。
从左到右枚举每一个数,假设每一个数都选择,当当前的总和小于0的时候,我们就把从开始位置到当前位置之间的负数中最小的一个删掉。
为什么这样做呢?
假设枚举到第 i i i个的时候,总和 s u m sum sum从正数变成负数。再假设此时我们选择了 k k k个数(不算第 i i i个)。
那么很明确的是, s u m sum sum是由于第 i i i个数的加入才变成了负数, 说明第 i i i个数一定是负数。那么我们当然可以选择删除第 i i i个数,这样的话,我们就能保证 s u m sum sum依然是正数。
但不选第 i i i个数就是最优解吗?其实不一定的。
如果在 1 1 1到 i i i之间存在一个小于第 i i i个数的最小的负数。如果我们删除了这个最小的负数,选择了第 i i i个数,我们将这两个数字记作 m i n min min和 p p p。那么此时的总和就是 s u m − m i n + p sum-min+p sum−min+p由 m i n min min小于 p p p所以 p − m i n p-min p−min是大于0的。
而此时我们选了几个数呢?选择第 i i i个数,我们此时总共选了 k + 1 k+1 k+1个数,删除最小的负数,即再减一,所以总共还是选择了 k k k个数。
其实很容易证明,当我们经过上述操作后,我们的 s u m sum sum是从 1 1 1到 i i i中选择 k k k个数时,最大的数字和。式子 s u m + p − m i n v sum+p-minv sum+p−minv就可以证明,因为 m i n v minv minv是最小的,所以这个式子是最大的。
也就是说,通过上述的操作,我们维护的都是选择 k k k个数时的最优解( s u m sum sum最大)。
通过刚才的 e a s y easy easy版本的讲解,我们也知道,选择相同个数的数字时,总和越大越好,总和越大说明我们后续的选择越多。
不妨看出,通过上面的操作,我们的 k k k是不受影响的, 即这样调整不会使得我们的答案变小。
如果感性认知的话,就是我们时刻保持最优解去看能不能喝下一瓶。
综上,我们的做法可以描述为,从左到右遍历,利用总和 s u m sum sum记录,只要 s u m sum sum小于0了,我们就删除遍历过的数中的最小负数。
在一堆数字中选出一个最值,我们可以使用优先队列。
我们的时间复杂度即 O ( n l o g n ) O(nlogn) O(nlogn)。
而我们发现,这个贪心过程中我们出现了反悔的操作,即我们一开始喝了一瓶,但是后来发现喝的这一瓶不是最优解,那么我们就反悔了,这一瓶不喝了。这种贪心就被称为反悔贪心。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2e5 + 10;
ll a[N], f[N];
void solve()
{
int n;
cin >> n;
for(int i = 0; i < n; i ++ )
cin >> a[i];
priority_queue<int>q;
ll ans = 0, sum = 0;
for(int i = 0; i < n; i ++ )
{
sum += a[i];
ans ++;
if(a[i] < 0)
q.push( - a[i]);
if(sum < 0)
{
sum += q.top();
q.pop();
ans --;
}
}
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
}
























 578
578











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








