物理实验报告·交直流电桥

交直流电桥原理与应用实验报告

一、实验目的

  1.学习掌握直流电桥测电阻的工作原理和特点；
  2.学习掌握正确使用直流电桥测量电阻的方法；
  3.了解铜电阻和热敏电阻的电阻-温度特性；
  4.学习和初步掌握非平衡电桥的设计方法。

二、实验原理

1.惠斯通电桥原理

图1 惠斯通电桥原理图

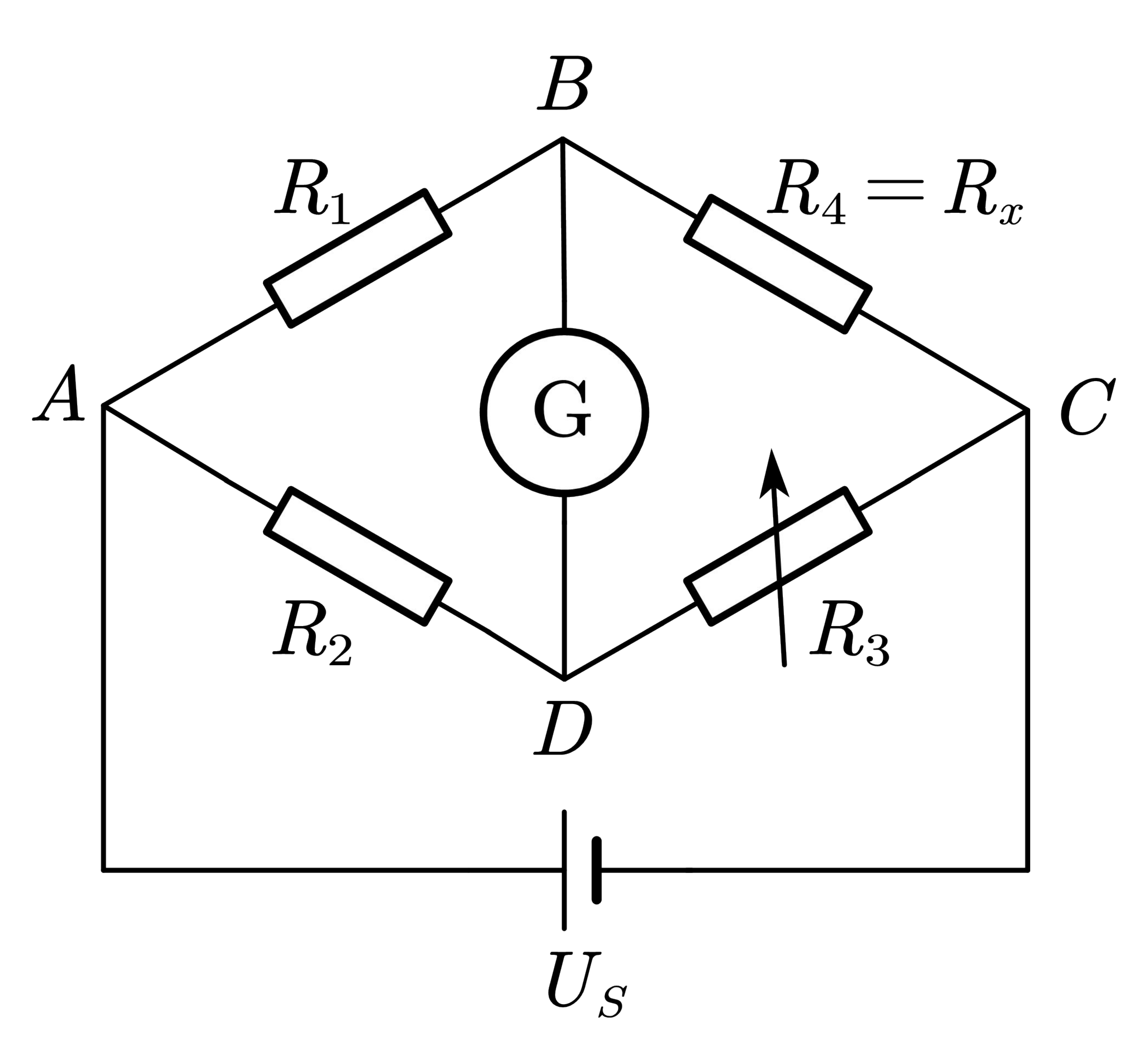
  图1为惠斯通电桥的原理图，$R_1,R_2,R_3$是三个可调标准电阻，$R_x$是被测电阻，$\mathrm{G}$是检流计，$U_S$是直流电源。当$B,D$二点等电位时称为电桥平衡。电桥达到平衡的条件为
$$\frac{R_1}{R_2}=\frac{R_4}{R_3}\text{\hspace{1em}(1)}$$

2.非平衡电桥原理

图2 非平衡电桥原理图

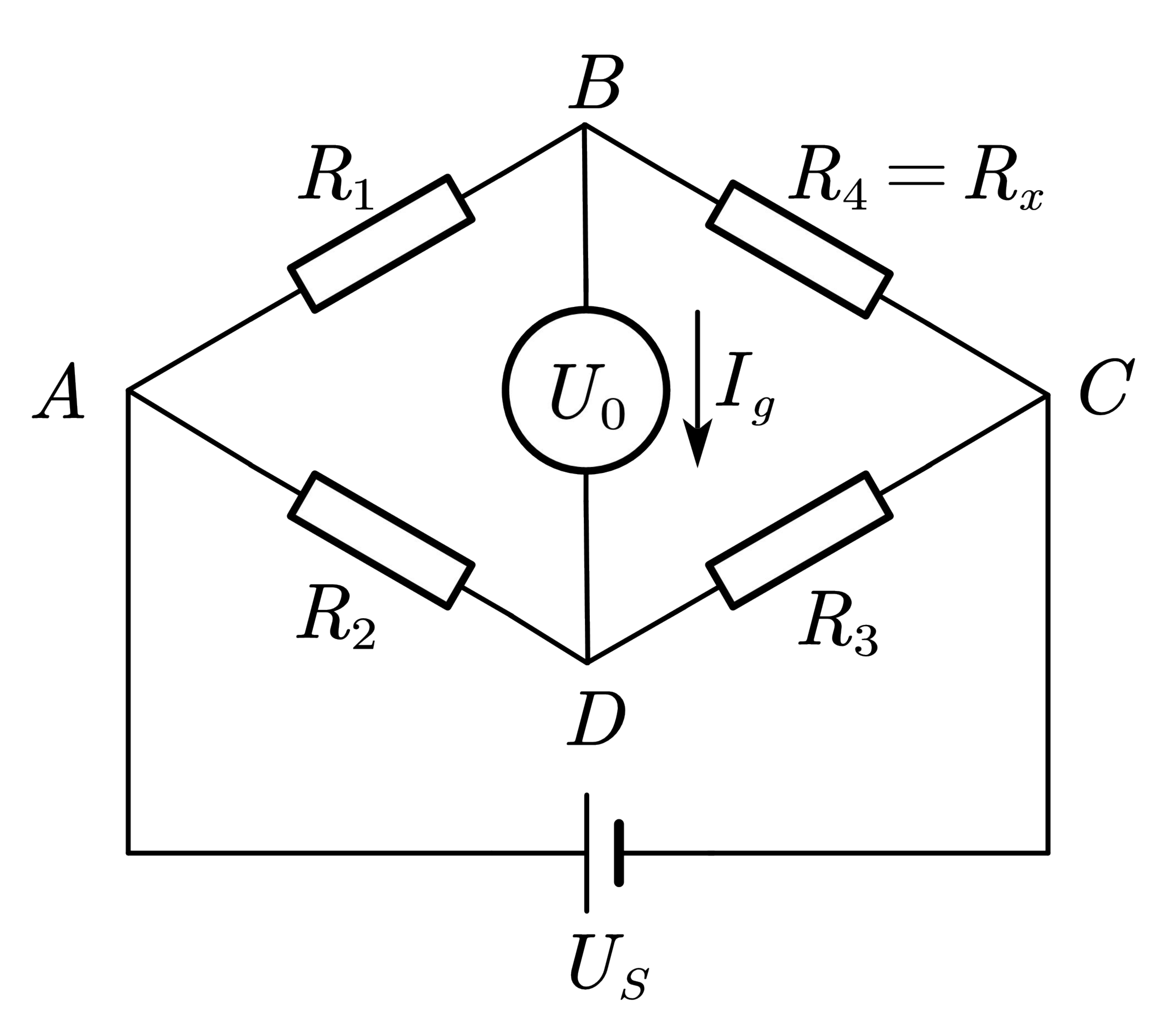
  图2是非平衡电桥原理图，其中$I_g\ne 0$.通过测量$B,D$之间的电压$U_0$得到$R_x$.这分为两类：
  输出对称（卧式电桥）：$R_2=R_3$
  电源对称（立式电桥）：$R_1=R_2$
  对于电压表而言，其内阻$R_g$非常大，可以认为$R_g\to \infty$，有：
$$U_0=\frac{R_2{R}_4-R_1{R}_3}{(R_1+R_4)(R_2+R_3)}\text{\hspace{1em}(2)}$$

  固定$R_1,R_2,R_3$，当$R_4$随某非电量$x$（如温度、压力等）变化而变化时，$R_4(x)$获得一增量$\Delta R(x)$，上式变为：
$$U_0(x)=\frac{R_2{R}_4+R_2\Delta R(x)-R_1{R}_3}{(R_1+R_4+\Delta R(x))(R_2+R_3)}\cdot U_S\text{\hspace{1em}(3)}$$

  对于卧式电桥，$R_1=R_4=R$，$R_2=R_3=R^{\prime }$.若电阻变化很小，记$\Delta (x)<<R_1+R_4$，则可认为电桥的输出电压为：
$$U_0(x)=\frac{R_2{R}_4+R_2\Delta R(x)-R_1{R}_3}{(R_1+R_4+\Delta R(x))(R_2+R_3)}\cdot U_S=\frac{\Delta R(x)}{4R}{U}_S\text{\hspace{1em}(4)}$$

  若电阻变化很大，即$\Delta R(x)<<R_1+R_4$不成立时，应将$(4)$式修正为：
$$U_0(x)=\frac{\Delta R(x)U_S}{4R+2\Delta R(x)}\text{\hspace{1em}(5)}$$

  对于立式电桥，$R_3=R_4=R$，$R_1=R_2=R^{\prime }$.若电阻变化很小，即$\Delta R(x)<<R_1+R_4$，则可以认为电桥的输出电压为：
$$U_0(x)=\frac{R_2{R}_4+R_2\Delta R(x)-R_1{R}_3}{(R_1+R_4+\Delta R(x))(R_2+R_3)}\cdot U_S=\frac{R^{\prime }\Delta R(x)}{(R+R^{\prime }{)}^2}{U}_S\text{\hspace{1em}(6)}$$

  若电阻变化很大，即$\Delta R(x)<<R_1+R_4$不成立时，应将$(6)$式修正为：
$$U_0(x)=\frac{R^{\prime }\Delta R(x)U_S}{(R+R^{\prime })(R+R^{\prime }+\Delta R(x))}\text{\hspace{1em}(7)}$$

3.铜热电阻特性
  铜热电阻是通过金属在温度变化时本身电阻也随之发生变化的原理来测量温度的一种传感器。$Cu50$型铜电阻阻值$R_t=R_0(1+\alpha t)$，其中$R_0$为其在$t=0^{\circ }\mathrm{C}$时的电阻值$50\Omega$，$\alpha$称为电阻的温度系数，约为$4.3\times 10^{-3}{}^{\circ }{\mathrm{C}}^{-1}$.另一种常用的热电阻是铂，它的优点是电阻稳定、准确、线性度较好；缺点是电阻变化小，响应速度慢，且成本较高。
4.热敏电阻特性
  热敏电阻是一种负电阻温度系数的半导体金属氧化物电阻，是一种典型的非线性电阻，$R_t=R_{25}{\mathrm{e}}^{B_n(\frac{1}{T}-\frac{1}{298})}$，其中$R_{25}$是其在$t=25^{\circ }\mathrm{C}$时的电阻值。$B_n$为材料常数，制作时不同的处理方法其值不同。它的优点是灵敏度高、响应速度快，缺点是非线性、温度范围有限、自发热。

三、实验仪器

  FQJ型非平衡直流电桥，温度控制器，升温加热炉。

四、实验内容

  1.用平衡电桥测量$Cu50$型铜电阻的温度特性
  （1）连接电路，调节$R_1=1\mathrm{k\Omega },R_2=5\mathrm{k\Omega }$，将功能选择旋钮置于“DC 0-15V”挡。
  （2）调节$R_n$使电压表示数为零，电桥平衡。记录各桥臂电阻及温度。
  2.用卧式电桥测量$Cu50$型铜电阻$R(t)$及电阻温度系数$\alpha$
  （1）连接电路，调节桥臂电阻值使$R_2=R_3=R^{\prime }=1\mathrm{k\Omega }$.
  （2）在室温下调节$R_n$使得电压表示数为尽可能接近零，记录温度、电压和$R_n$，后续升温过程中$R_n$保持不变。
  （3）加热升温，每隔$3^{\circ }\mathrm{C}$测一个点，记录电压值和温度，共测$10$个点。
  （4）用最小二乘法求电阻值$R_0$和温度系数$\alpha$，下厨经验方程$R_t=R_0(1+\alpha t)$.
  3.用立式电桥测量$MF51$型热敏电阻的温度特性
  （1）连接线路，调节桥臂电阻使$R_1=R_2=R^{\prime }=100\Omega$.
  （2）在室温下调节$R_n$使得电压表示数为零，记录温度和$R_n$，后续升温过程中$R_n$保持不变。
  （3）加热升温，每隔3℃测一个点，记录电压值和温度，共测10个点。
  （4）作$MF51$型热敏电阻的$R(T)\sim T$和$\ln R(T)\sim 1/T$曲线，并用最小二乘法求出材料常数$B_n$和$R_{25}$，写出经验方程。
  4.交流电桥测电容
  （1）设置电源为正弦波，调节频率为$(1000\pm 5)\mathrm{Hz}$.
  （2）用$2$根导线将交流电压表的测量端连接到电桥的电源端，调节“幅度调节”旋钮，使得交流电压表示数在$(2.00\pm 0.02)\mathrm{V}$范围内。
  （3）连接电路，调节桥臂电阻$R_a=100\mathrm{\Omega },R_b=120\mathrm{\Omega }$.
  （4）交替调节$C_n,R_n$，使得交流检流计示数最小。然后逐渐增大交流检流计灵敏度，重复调节，直至灵敏度最大。电桥平衡后，记录$R_a,R_b,C_n,R_n$的值。
  5.交流电桥测电感
  （1）按照交流电桥测电容中的步骤（1）和（2）设置电源。
  （2）连接电路，调节桥臂电阻$R_a=100\Omega ,R_b=100\Omega$.
  （3）交替调节$C_n,R_n$，使得交流检流计示数最小。然后逐渐增大交流检流计灵敏度，重复调节，直至灵敏度最大。电桥平衡后，记录$R_a,R_b,C_n,R_n$的值。

五、数据处理

1.平衡电桥测量$Cu50$型铜电阻在室温下的电阻

图3 测量铜电阻电路图

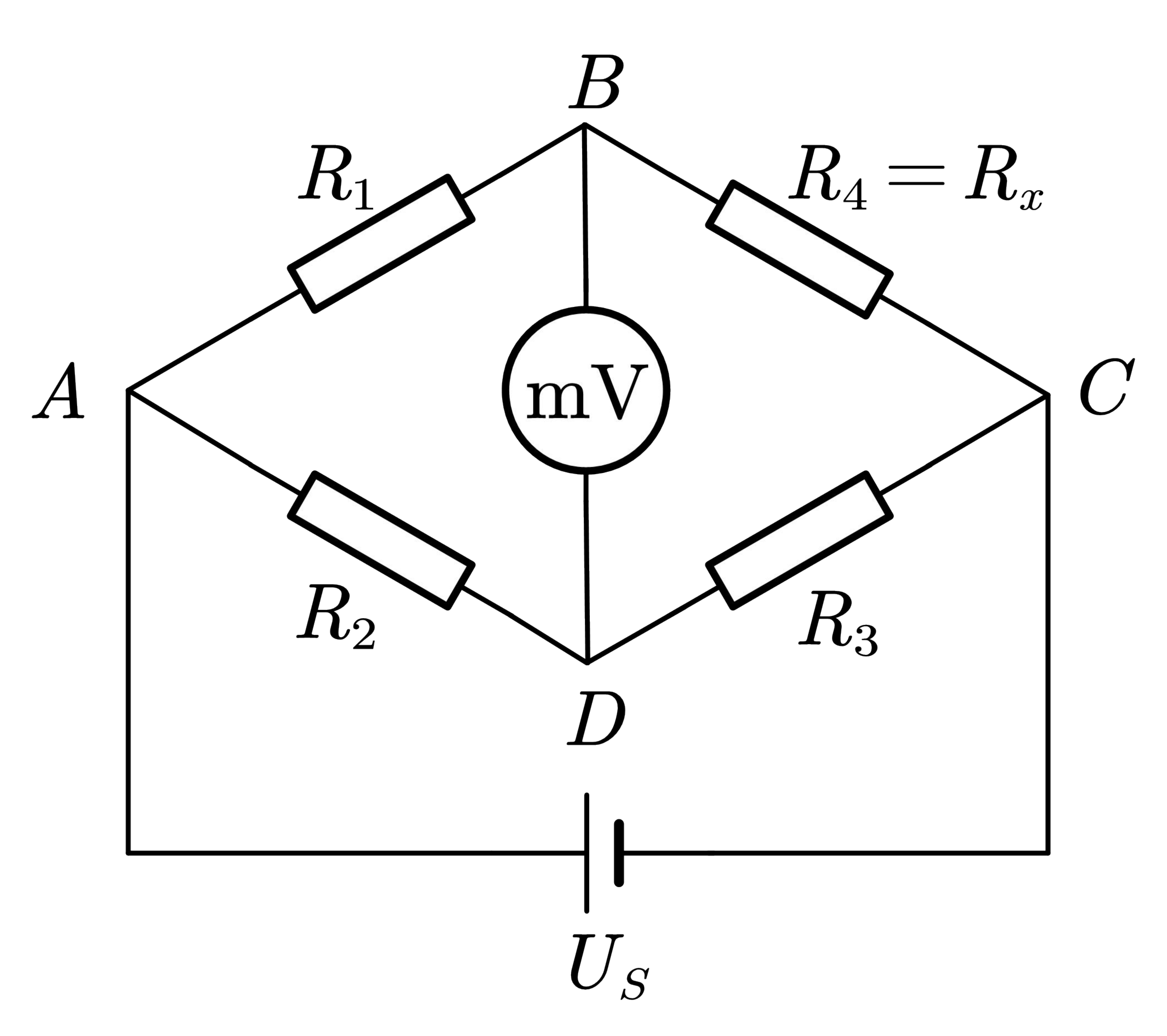
  按照图3连接好电路，在$R_1=1\mathrm{k\Omega },R_2=5\mathrm{k\Omega },U_S=2.999\mathrm{V}$，室温$t=22.7^{\circ }\mathrm{C}$下，测得电桥平衡时$R_3=278.1\Omega$.
  根据电桥平衡的条件式$(1)$，求得$R_x=55.62\Omega$.
  理论上有$R_x=R_0(1+\alpha t),\alpha =0.0043^{\circ }{\mathrm{C}}^{-1}$，计算得到$t=22.7^{\circ }\mathrm{C}$下的理论值$R_{x理}=54.88\Omega$.
  所以实验的百分误差为$\left|\frac{R_{x实}-R_{x理}}{R_{x理}}\right|\times 100\%=1.4\%$.
2.用卧式电桥测量$Cu50$型铜电阻的温度特性
  整理实验中得到的数据，如表1所示：

表1 卧式电桥测量铜电阻温度特性数据表

序号	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$
$t{/}^{\circ }\mathrm{C}$	$24.3$	$27.3$	$30.3$	$33.3$	$36.3$	$39.3$	$42.3$	$45.3$	$48.3$	$51.3$
$U/\mathrm{mV}$	$0.43$	$8.89$	$17.20$	$25.36$	$33.67$	$41.79$	$49.67$	$57.43$	$65.41$	$73.38$
$R_x/\Omega$	$56.13$	$56.76$	$57.39$	$58.00$	$58.62$	$59.23$	$59.82$	$60.40$	$61.00$	$61.59$

  作出$R_x\sim t$曲线图如图4所示。

图4 铜电阻温度特性图

  用计算机拟合直线得$R_x=0.2018t+51.266$.因此，$R_0=51.266\Omega ,\alpha =\frac{0.2018}{51.266}{}^{\circ }{\mathrm{C}}^{-1}\approx 0.00394^{\circ }{\mathrm{C}}^{-1}$.
  $R_0$的百分误差$\left|\frac{R_{0测}-R_{0实}}{R_{0实}}\right|\times 100\%=2.5\%$.
  $\alpha$的百分误差$\left|\frac{{\alpha }_{测}-{\alpha }_{0实}}{{\alpha }_{0实}}\right|\times 100\%=8.4\%$.
3.交流电桥测量电容

图5 测量电容电路图

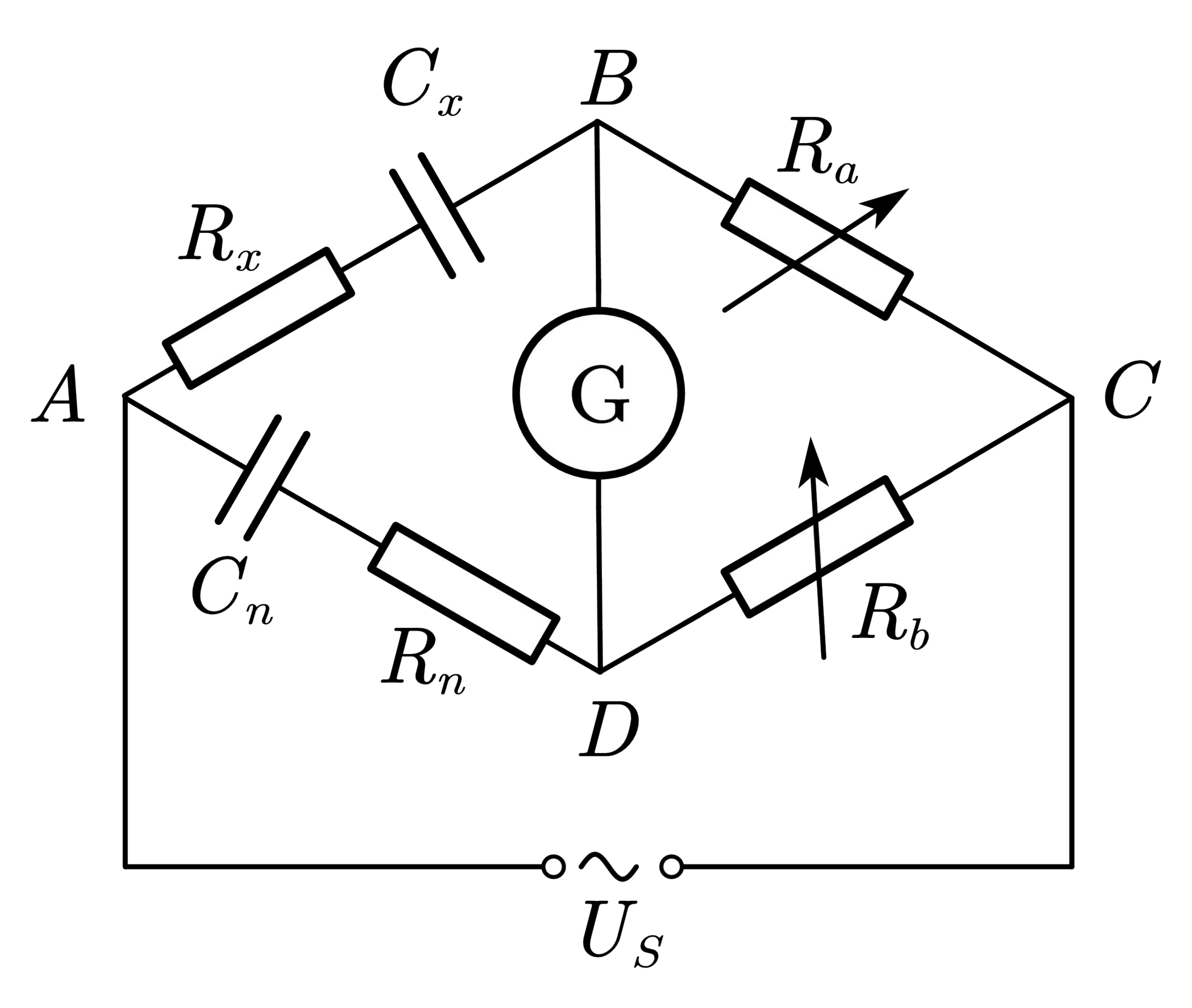
  按照图5连接好电路，在$R_a=100\Omega ,R_b=120\Omega$下，测得电桥平衡时$C_n=0.832\mathrm{F},R_n=0.7\Omega$.
  故待测电容$C_x=\frac{R_b{C}_n}{R_a}=0.998\mu \mathrm{F}$，损耗电阻$R_x=\frac{R_a{R}_n}{R_b}=0.583\Omega$，损耗因子$\tan \delta =R_x{C}_x\omega =3.66\times 10^{-3}$.
4.交流电桥测量电感

图6 测量电感电路图

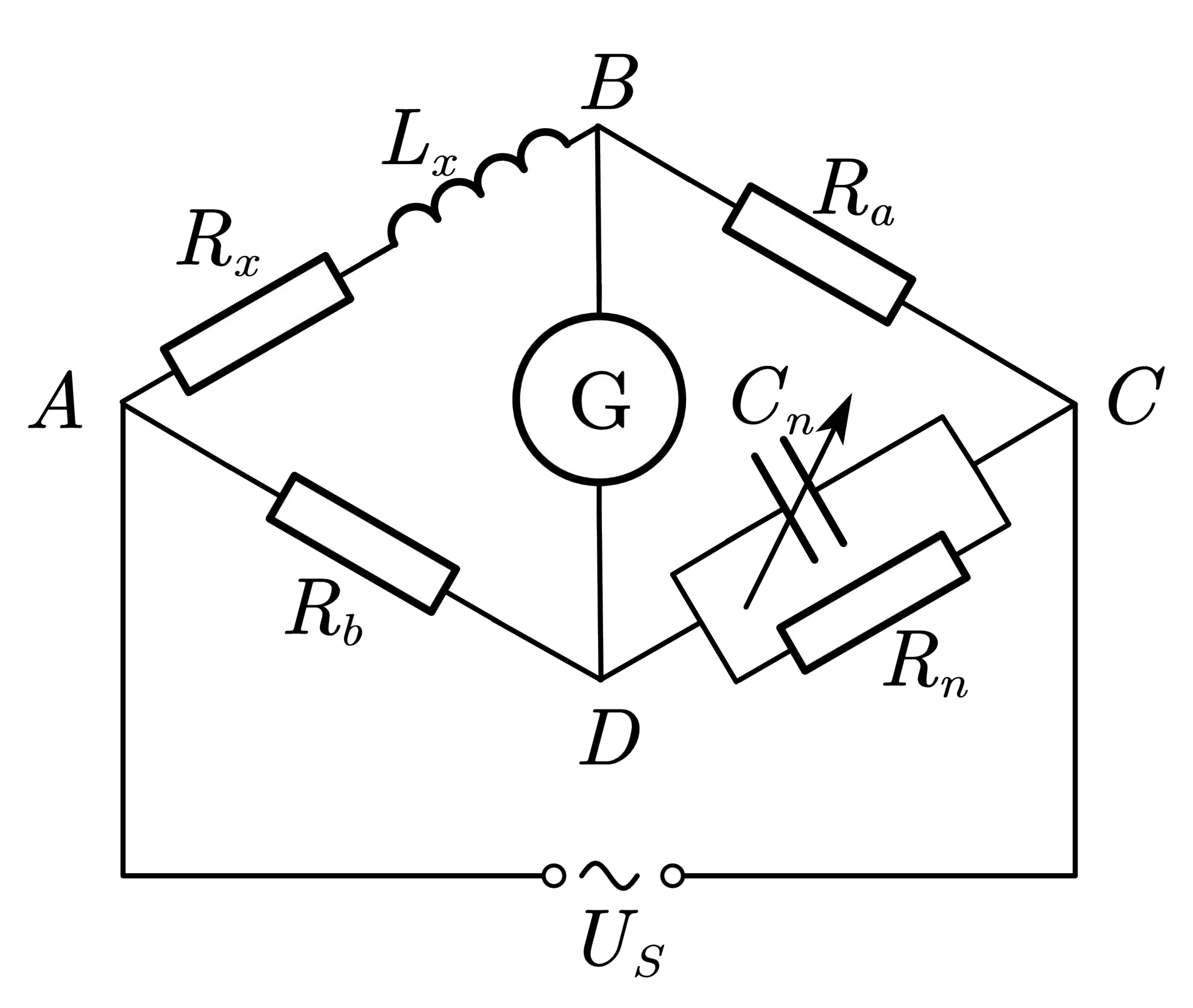
  按照图6连接好电路，在$R_a=R_b=100\Omega$下，测得电桥平衡时$C_n=0.491\mu \mathrm{F},R_n=2200\Omega$.
  故待测电感$L_x=R_a{R}_b{C}_n=4.91\mathrm{mH}$，损耗电阻$R_x=\frac{R_a{R}_b}{R_n}=4.54\Omega$，品质因数$Q=\frac{\omega L_x}{R_x}=6.79$.

六、结果分析

1.误差分析
  （1）本实验中“用卧式电桥测量$Cu50$型铜电阻的温度特性”的测量会存在较大误差。原因有二：一是个数字仪器指示的电压（或温度）存在一定的延迟，可能不是当前时刻的值；二是温度逐渐上升时电压值随之快速变化，无法准确记录正确的电压值。同时，由于计算$R_x$时使用了近似公式$(4)$，这也会在一定程度上导致误差。
  （2）在“交流电桥测量电容”实验中，电阻箱的精度只有$0.1\Omega$，这就导致测量值$R_n=0.7\Omega$存在一定误差。
2.改进方法
  （1）可以采用更先进的数字测量系统，避免人反应时间带来的误差；也可以换用更友好的加热仪器，防止加热仪器在挂0挡后温度仍然要上升一段时间的问题。
  （2）提高电阻箱精度，从而增加测量值$R_n$的有效数字。

七、思考题

1.在平衡电桥和非平衡电桥实验中，电源电压的准确度对测量结果的影响相同吗？为什么？
  应该是不相同的。在平衡电桥实验中，$R_x$的计算式为$R_x=R_a{R}_n/R_b$，其中不含电源电压，即电源电压的测量准确度对其无影响。而非平衡电桥实验中，计算$R_t$需要用到电源电压$U_0$，所以电源电压的准确度对测量结果是有影响的。
2.使用交流电桥平衡法测量电容、电感时，通常需要先粗测待测元件的值，以便合理地配置各桥臂的初始值。尝试利用本实验的设备设计实验方案，粗测待测电容、电感。

图7 粗测电容电路图

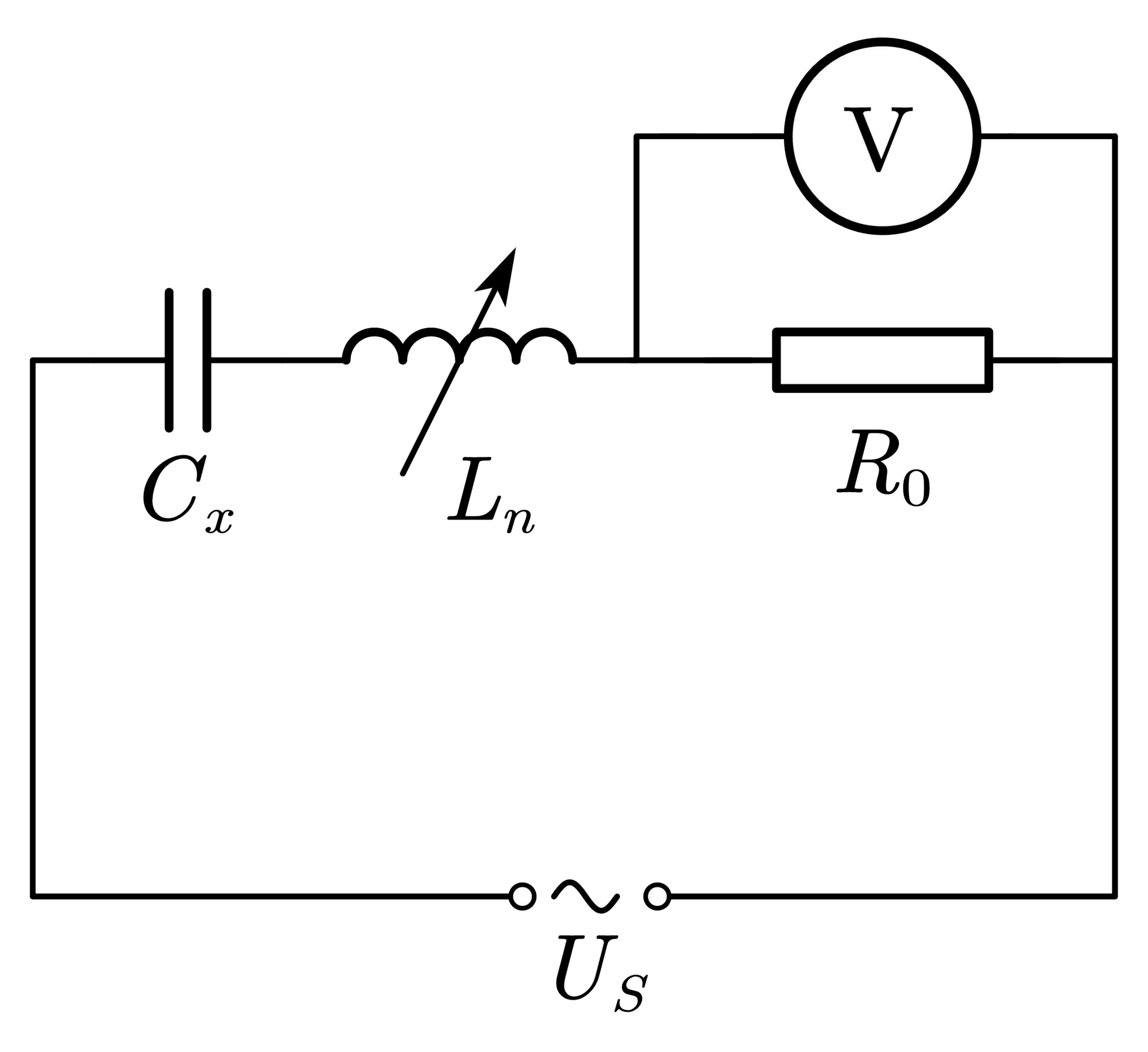
  采用图7测量$C_x$.连接好电路后，调节$L_n$，使电压表示数最大，这说明回路中电流达到最大，总阻抗最小，电路处于串联谐振状态。
  此时有$X_L+X_C=\omega L_n-\frac{1}{\omega C_x}=0$，所以
$$C_x=\frac{1}{{\omega }^2{L}_n}\text{\hspace{1em}(8)}$$

  根据式$(8)$粗略估计待测电容。同理，将上述电路中$C_x$换成$C_n$，$L_n$换成$L_x$，调节$C_n$使电压表示数最大，即可按照式$(9)$求出粗略的电感$L_x$：
$$L_x=\frac{1}{{\omega }^2{C}_n}\text{\hspace{1em}(9)}$$

3.交流电桥的桥臂是否可以任意选择不同性质的阻抗元件组成？应如何选择？
  不行。由交流电桥的平衡条件$Z_1{Z}_4=Z_2{Z}_3$，若$Z_1,Z_4$为纯电阻，那么$Z_2,Z_3$要么都是纯电阻，要么一个呈感性$(X>0)$，另一个呈容性$(X<0)$.如果$Z_1,Z_2$为纯电阻，那么$Z_3,Z_4$要么都是呈感性，要么都呈容性。否则无论如何调节其大小，交流电桥都无法达到平衡。