二分（数学背景，边界问题，二分查找，二分答案）

最新推荐文章于 2025-03-31 17:46:36 发布

shenkerenshi

最新推荐文章于 2025-03-31 17:46:36 发布

阅读量906

点赞数 3

分类专栏：基础算法文章标签： c语言算法

本文链接：https://blog.csdn.net/weixin_72223753/article/details/128633869

版权

基础算法专栏收录该内容

4 篇文章

订阅专栏

文章详细介绍了二分法的数学背景，目的以及应用于求解方程近似解的步骤和复杂度。通过实例展示了从整数二分到浮点二分的过程，包括二分查找在有序数组中的应用，如寻找特定值、大于等于值的最小下标等。同时，讨论了二分法的边界问题和优化策略，并提供了相关编程实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二分法的数学背景

目的

关于二分法的目的，这里引用同济大学数学系出版的《高等数学》第七版上册中关于二分法的相关内容。（文段内容多，要有一点耐心~）

在科学技术问题中，经常会遇到求解高次代数方程或其他类型的方程的问题.要求得这类方程的实根的精确值，往往比较困难，因此就需要寻求方程的近似解。

求方程的近似解，可分两步来做。

第一步是确定根的大致范围。具体地说，就是确定一个区间 [a,b]，使所求的根是位于这个区间内的唯一实根，这一步工作称为根的隔离，区间[a,b]称为所求实根的隔区。由于方程 f(x)=0的实根在几何上表示曲线 y=f(x)与×轴交点的横坐标，因此为了确定根的隔离区间，可以先较精确地画出y=f(x)的图形，然后从图上定出它与x轴交点的大概位置.由于作图和读数的误差，这种做法得不出根的高精确度的近似值，但一般已可以确定出根的隔离区间。

第二步是以根的隔离区间的端点作为根的初始近似值，逐步改善根的近似值的精确度，直至求得满足精确度要求的近似解。完成这一步工作有多种方法，这里我们介绍三种常用的方法一一二分法、切线法和割线法，按照这些方法，编出简单的程序，就可以在计算机上求出方程足够精确的近似解。

由上方的书本内容可以知道，二分法的出现是为了求解方程的近似解。

理论（包含前提和思路及复杂度）

仍然引用上述书本中对于二分法理论的解释。

前提

f(x)在[a,b]上连续且单调有界。

思路

设(x)在区间 [a,b]上连续， f(a)·f(b)<0，且方程f(x)=0在 (a,b)内仅有一个实根，于是 [a,b]即是这个根的一个隔离区间.

取[a,b]的中点 ξ1 =(a+b)/2，计算f(ξ1)。

如果 f(ξ1)=0,那么ξ=ξ1；

如果 f(ξ1)与f(a)同号，那么取 a1=ξ1，b1=b，由f(a1)·f(b1)<0，即知a1<ξ<b1，且b1-a1=(b-a)/2;
如果 f(ξ1)与f(b)同号，那么取 a1=a，b1=ξ1，也有a1<ξ<b1，及b1-a1=(b-a)/2；
总之，当 ξ≠ξ1时，可求得 a1<ξ<b1，且b1-a1=(b-a)/2。

以 [a1,b1]作为新的隔离区间，重复上述做法，当ξ≠ξ2=(a1+b1)/2时，可求得a2<ξ<b2，且b2-a2=(b-a)/(2^2)。
如此重复n次，可求得 an<ξ<bn，且 bn-an=(b-a)/(2^n)。由此可见，如果以an或bn作为ξ的近似值，那么其误差小于(b-a)/(2^n)。

复杂度

显然有经过n次二分后，区间会缩小到(b - a)/2n。给定a、b和精度要求ε，可以算出二分次数n，即满足(b - a)/(2^n)<ε。所以，二分法的复杂度是O(log2 n)的。

二分法由简单到复杂的循序渐进

整数二分

二分查找

先来举一个简单的例子，如下是一个有序数列a[6]。（对应单调函数）

下标	0	1	2	3	4	5
数值	1	3	4	4	6	7

现在需要查找数组中的元素4

思路一：遍历数组a，查找出数字4的位置，复杂度为O(n)。—— 粗暴搜索

思路二：使用二分法。（比之思路一高效）

代码实现

头文件、函数声明和主函数

#include<stdio.h>


int Simple_Search(int a[], int left, int right, int key);//查找到就返回
int Problem1_Search(int a[], int n, int key);//问题一：查找等于key的最小下标
int Problem2_Search(int a[], int n, int key);//问题二：查找大于等于key的最小下标
int Problem3_Search(int a[], int n, int key);//问题三：查找大于key的最小下标


int main() {
    int a[255], n, i, key;
    printf("输入一组有序数列（升序）\n");
    for (i = 0; scanf_s("%d", &a[i]) == 1; i++) {
        if (getchar() == '\n')break;
    }//输入任意长度的数组
    n = i + 1;
    //记录数组长度，+1是因为最后一轮循环中break掉了i++没有执行
    printf("输入要查找的数值\n");
    scanf_s("%d", &key);
    printf("%d\n", Simple_Search(a, 0, n - 1, key));//查找到就返回
    printf("%d\n", Problem1_Search(a, n, key));//问题一
    printf("%d\n", Problem2_Search(a, n, key));//问题二
    printf("%d\n", Problem3_Search(a, n, key));//问题三
    printf("%d\n", Problem3_Search(a, n, key) - Problem2_Search(a, n, key));//问题四
    return 0;
}

代码一（查找到就返回）

int Simple_Search(int a[], int left, int right, int key) {
    int middle = left + (right - left) / 2;//找到中值
    if (a[middle] == key) {
        return middle;
        //找到即返回位置，结束函数递归
    }
    else if (a[middle]<key) {
        Simple_Search(a, middle + 1, right, key);
    }//如果middle位置的值小于查找值，则搜索middle+1~right
    else if (a[middle] > key) {
        Simple_Search(a, left, middle - 1, key);
    }//如果middle位置的值大于查找值，则搜索left~middle-1
}

值得注意的是，计算middle的式子中我没有使用(left+right)/2，原因是left和right的和可能超出int的范围导致溢出出错（当然我上方主函数开的数组长度很小，但如果需要对大量数据进行处理，将数组开得很大，就很有可能出现这种情况）。安全起见，我们使用left+(right-left)/2。

运行结果

显然这种代码没法处理很多问题，如要查找的数值可能在数组中并不存在，甚至key=4时连所有的4的位置都无法找出，功能非常有限。

因此针对我们的需求，我们提出以下几个问题：

问题一：查找等于key的最小下标（最大下标）

问题二：查找大于等于key的最小下标（小于等于最大下标）

问题三：查找大于key的最小下标（小于最大）

问题四：统计等于key的位置个数

我以下几乎没有介绍上面几个问题括号内的那些代码怎么实现，其实差不多，但是有细节不同，很容易被忽略，而且很致命！如果有人注意到并且不好想明白的话可以直接下滑到最后边界问题处~

代码二（问题一：等于）

int Problem1_Search(int a[], int n, int key) {
    //上面用递归完成，以下函数都用循环完成。
    int left = 0, right = n - 1;
    while (left < right) {
        //这里循环条件只能是<不能是<=
        //如果加上=则循环无法结束
        int middle = left + (right - left) / 2;
        if (a[middle] == key) {
            right = middle;//注意此时是middle不是middle-1
            //原因：保留上一个查找到的位置，直到后面又查找到符合条件的才被替换掉
            // 如果要用middle-1的话要再定义一个num来记录middle的位置
            // 变成int ans=middle;right=middle-1;
            // 此时循环条件要变成<=
            // 否则最后一轮循环无法进行 返回值也要变成ans
            //（查找最大的话把right=middle改为left=middle）
        }//当找到一个位置后将位置记录下来以后继续向前（向后）查找是否还有符合的位置
        else if (a[middle] > key) {
            right = middle - 1;
        }
        else if (a[middle] < key) {
            left = middle + 1;
        }
    }
    return left;
}

运行结果

代码三（问题二：大于等于）

跟上方类似，不再在代码中注释赘述。

要说明的是特殊情况：如果没有大于等于key的数，返回的是数组最后的位置。

int Problem2_Search(int a[], int n, int key) {
    int left = 0, right = n - 1;
    while (left < right) {
        int middle = left + (right - left) / 2;
        if (a[middle] >= key) {
            right = middle;
        }
        else left = middle + 1;
    }
    return left;
}

运行结果

代码四（问题三：大于）

其实跟代码三几乎一模一样，唯一的区别就是if条件里的>=改成了>（所以下面代码不看也行）

（就是有点强迫症想整齐点）

特殊情况也类似，没有大于查找数值的就返回最后位置。

int Problem3_Search(int a[], int n, int key) {
    int left = 0, right = n - 1;
    while (left < right) {
        int middle = left + (right - left) / 2;
        if (a[middle] > key) {
            right = middle;
        }
        else left = middle + 1;
    }
    return left;
}

运行结果

代码五（问题四：等于个数）

这里没有代码啦！

因为这是一个有序的数组，所以问题三的返回值减去问题二的返回值（大于的第一个位置减去大于等于的第一个位置）就是要的等于key的位置个数。（输出代码在主函数有体现）

运行结果

与C++中STL的联系

事实上，上述的问题二和问题三的代码可以解决上述所有问题，它们分为对应STL中的lower_bound()和upper_bound()函数。

　　（1）查找第一个大于key的元素的位置：upper_bound() —— 问题三

　　（2）查找第一个大于等于key的元素：lower_bound() —— 问题二

　　（3）查找第一个等于key的元素：lower_bound()且 = x —— 问题一

　　（4）查找最后一个等于key的元素：upper_bound() -1且 = x —— 问题一

　　（5）查找最后一个小于等于key的元素：upper_bound() -1 —— 问题三

　　（6）查找最后一个小于key的元素：lower_bound() -1 —— 问题三

　　（7）单调序列中数key的个数：upper_bound() - lower_bound() ——问题四

二分答案

二分法的典型应用有：最小化最大值、最大化最小值。—— 运用二分答案

二分答案，顾名思义，运用二分法查找答案。

“二分”在上述二分查找中已经阐明清楚。

那么什么是“答案”？

答案就是确定答案范围，通过枚举判断找出答案。

二分答案的实质就是把前面二分查找的数列变为我们答案的所有可能性。

模板

while (left <= right) {
        int ans;
        //记录答案（这种记录答案的模板形式在上方没有记录答案的代码中提到过）
        //这个是通用模板，不会在循环中出错——最优方案！
        //不用ans记录而return left/right的可能因为边界出现问题！（边界问题在结尾会阐述）
        int middle = left+(right-left)/2;
        if (check(middle)){//检查条件
            ans = middle;//记录答案
            …//根据条件要求移动left（或right）
        }
        else …//移动right（或left）
}

根据模板可以知道，在解决题目的过程中，我们需要面对的就是如何建模和设置check函数。

以下用例题来具体说明更加直观。

一、P1182 数列分段 Section II

链接：数列分段

最小化最大值（使最大值尽量小）

题目描述

对于给定的一个长度为N的正整数数列 A 1∼N，现要将其分成 M（M≤N）段，并要求每段连续，且每段和的最大值最小。

关于最大值最小：

例如一数列 4 2 4 5 1 要分成 33 段。

将其如下分段：

[4 2][4 5][1]

第1段和为 6，第 2 段和为 9，第 3 段和为 1，和最大值为 9。

将其如下分段：

[4][2 4][5 1]

第1段和为 4，第 2 段和为 6，第 3 段和为 6，和最大值为 6。

并且无论如何分段，最大值不会小于 6。

所以可以得到要将数列 4 2 4 5 1 要分成 3 段，每段和的最大值最小为 6。

输入格式

第 1 行包含两个正整数 N,M。

第 2 行包含 N 个空格隔开的非负整数 Ai，含义如题目所述。

输出格式

一个正整数，即每段和最大值最小为多少。

解题思路

在此题中，我们首先要确定答案的范围。显然，答案最小可能是数列中的最大值（记为 left），最大可能是所有数的和（记为 right），再根据枚举出的答案再判定答案是否正确可以解决该题。

但如果简单粗暴地一个一个枚举答案，显然时间复杂度高，因此在枚举答案的基础上再使用二分的思想降低时间复杂度。

代码实现

#include<stdio.h>
#include<stdbool.h>

int M, N, arr[100000];

bool check(int mid) {
    int num = 0, block = 1;
    for (int i = 0; i < N; i++) {
        if (num + arr[i] > mid) {
            num = arr[i];
            block++;
        }//超过猜测答案换下一段
        else num += arr[i];
    }
    return block <= M;
    //如果最小的段数小于等于应要分的段数，返回True，否则False
}

int main() {
    int left, right=0, mid, ans;
    scanf_s("%d %d", &N, &M);
    for (int i = 0; i < N; i++) {
        scanf_s("%d", &arr[i]);
        if (i == 0)left = arr[i];
        else if (arr[i] > left)left = arr[i];
        //left为arr中的最大值
        right += arr[i];//right为所有数值和
    }
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (check(mid)) {
            ans = mid;
            right = mid - 1;
        }//猜测答案值满足条件，找找有没有更小的
        else left = mid + 1;//不满足往大的找
    }
    printf("%d", ans);
}

运行结果

二、P8647 [蓝桥杯 2017 省 AB] 分巧克力

链接：分巧克力

最大化最小值（使最小值尽量大）

题目描述

儿童节那天有 K 位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。

小明一共有 N 块巧克力，其中第 i块是 Hi×Wi 的方格组成的长方形。

为了公平起见，小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足：

形状是正方形，边长是整数。

大小相同。

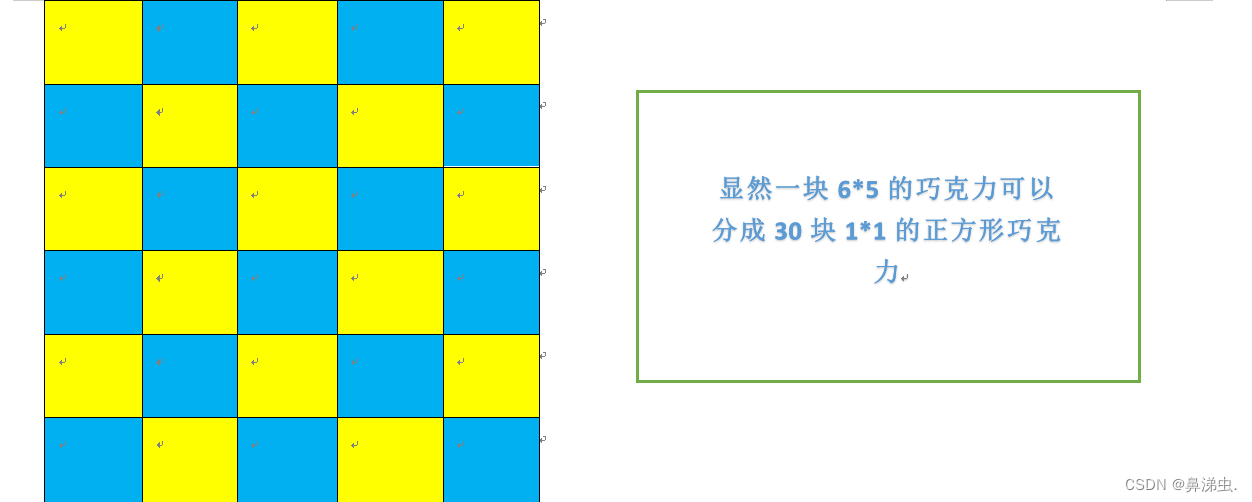
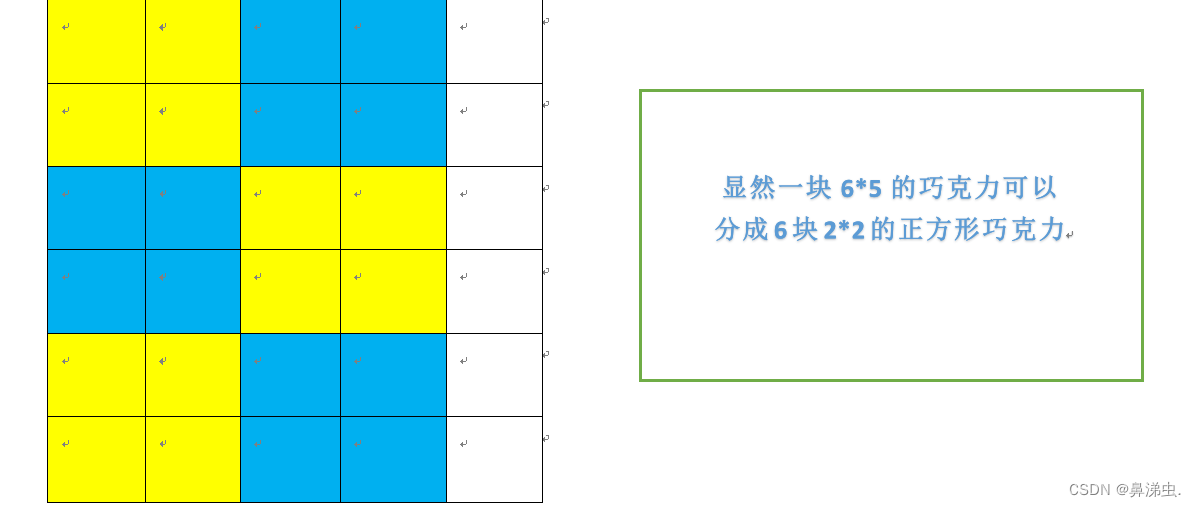
例如一块6×5 的巧克力可以切出6块2×2 的巧克力或者 2 块 3×3 的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式

第一行包含两个整数 N 和 K。(1≤N,K≤10^5)

以下 N行每行包含两个整数 Hi和 Wi。(1≤Hi,Wi≤10^5)

输入保证每位小朋友至少能获得一块1×1 的巧克力。

输出格式

输出切出的正方形巧克力最大可能的边长。

解题思路

解题思路和上一道题大致相同，只不过这次答案的范围有最小值取1，最大值取N块巧克力长的最大值和宽的最大值之间较小的那个（其实可以直接用10000，只多了一点点时间)

两个对比自己斟酌~

至于要是有人说直接用所有巧克力的最小边长（达咩！可能有些相比于其他超大巧克力块小不拉叽的巧克力根本用不到给抛弃了，而上面那种保证了至少有一块巧克力被用上了，勉强减小了right的值）

这里用图解来分析题目意思，以题中所给样例来分析。

代码实现

#include<stdio.h>
#include<stdbool.h>

int N, K, H[100000], W[100000];

bool check(int mid) {
    int k = K;//注意不要直接用K
    //K是全局变量，一旦改变就改变掉了回不去了
    for (int i = 0; i < N; i++) {
        k -= (H[i] / mid) * (W[i] / mid);
    }//减去每块巧克力可以切下的巧克力块数
    return k <= 0;
}

int main() {
    int max1, max2;
    scanf_s("%d %d", &N, &K);
    for (int i = 0; i < N; i++) {
        scanf_s("%d %d", &H[i], &W[i]);
        if (i == 0) {
            max1 = H[i]; max2 = W[i];
        }
        else {
            if (H[i] > max1)max1 = H[i];
            if (W[i] > max2)max2 = W[i];
        }
    }
    int left = 1, right = (max1 <= max2) ? max1 : max2;
    //right取长最大值和宽最大值两个之间较小的那一个
    int ans;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (check(mid)) {
            ans = mid;
            left = mid + 1;
            //找到往更大的找
        }
        else right = mid - 1;
        //不符合往小的找
    }
    printf("%d", ans);
    return 0;
}

运行结果

关于整数二分就先告一段落了，大家可以自己找题目多练练手。

浮点二分

浮点二分思路和整数二分是一模一样的，不过有一些小细节值得注意。

它就对于我刚开始数学背景里提到的求解方程的近似解就更贴近了。

这里直接给出模板和解析了。

模板

const double eps =1e-7;
//确定精度
//如果下面用for，可以不用提前定义eps
while(right - left > eps){
    //或者for(int i = 0; i<100; i++){
    double mid = left+(right-left)/2;
    if (check(mid)) right = mid;
    //不需要ans——left=mid而不是mid+1
    else left  = mid;
}

关于eps

《深入理解计算机系统》中这样写明：
浮点数普遍的作为实数运算的近似值的计算，是很有用的。这里说的是实数的近似值的计算，所以浮点数在计算机中其实是一种不精确的表示。它存在舍入误差。IEEE浮点标准用符号，尾数和阶码将浮点数的位表示划分为三个字段，单精度为32位，双精度为64位，因为表示方法限制了浮点数的范围和精度，浮点运算只能近似的表示实数运算。而 == 表示的是在计算机中的内存表示完全一样，因此使用 == 来表示两个浮点数的相等就会出现问题。

介于浮点数的表示方式，即使是理论上相同的值，如果两个数由于是经过不同的运算过程得到的，在低位（比如小数点后第十二位处)一般来说是不同的。这种现象会对一种运算产生致命的影响: ==。而C/C++中浮点数的==需要完全一样才能返回true，解决的办法是引进eps，来辅助判断浮点数的相等。

判断的修改：

eps的设置：有一个技巧：如果题目要求保留6位小数，那么eps设置为1e-8；如果题目要求保留4位小数，那么eps设置为1e-6。（事关输出位数小按四舍五入原则输出）

关于left和right的移动

与整数二分不同的是，这里无论是left的移动还是right的移动一律令其等于mid

left=mid+1 -> left=mid

right=mid-1 -> right=mid

关于for循环代替while循环

如果用for循环，由于每一次循环都进行了二分，执行100次，相当于实现了 1/(2^100)的精度，比一般要求的eps更为精确，但这也造成了循环次数增多，运行时间延长。（在对时间要求不高的情况下，for循环要简便些。）

例题：P1577 切绳子

链接：切绳子

最大化最小值（使最小值尽量大）

题目描述

有 N条绳子，它们的长度分别为 Li。如果从它们中切割出 K 条长度相同的绳子，这 K条绳子每条最长能有多长？答案保留到小数点后 2 位(直接舍掉 2 位后的小数)。

输入格式

第一行两个整数 N 和 K，接下来 N 行，描述了每条绳子的长度 Li 。

输出格式

切割后每条绳子的最大长度。答案与标准答案误差不超过 0.01或者相对误差不超过 1% 即可通过。

输入输出样例

输入

4 11

8.02

7.43

4.57

5.39

输出

2.00

说明/提示

对于 100% 的数据100000<Li≤100000.00, 0<n≤10000, 0<k≤10000

代码实现

#include<stdio.h>
#include<stdbool.h>

int N, K;
double L[100000];

bool check(double mid) {
    int k = K;
    for (int i = 0; i < N; i++) {
        k -= (int)(L[i] / mid);
        //记得转int型
    }
    return k <= 0;
}//跟分巧克力几乎一模一样

int main() {
    const double eps = 1e-4;
    double left = 0, right, mid;
    scanf_s("%d %d", &N, &K);
    for (int i = 0; i < N; i++) {
        scanf_s("%lf", &L[i]);
        if (i == 0)right = L[i];
        else if (L[i] > right)right = L[i];
        //right用所有绳子最长的一段长度（能缩短一点时间）
        //直接用100000.00也是可以的
    }
    while (right - left > eps) {
        mid = left + (right - left) / 2.0;
        if (check(mid)) {
            left = mid;
        }
        else right = mid;
    }
    printf("%.2lf", (int)(right * 100) / 100.0);
    //保留两位小数并且不四舍五入
    //这里不能用left输出（在洛谷内都会有一个数据报错）
    //其实计算出来精度已经满足要求了（我甚至试过了精度1e-7还是错误）
    //然后我一气之下直接试了1e-53（这下很多都超时了但是我看到那个数据AC了）
    //因此我认为问题在于题目要求是舍掉两位小数以后的小数而不是四舍五入
    //这让精度和输出要求产生了一点出入
    //当然如果是我理解错误大家也一定要指出！
    return 0;
}
//这道题先把数据乘以100以后进行整数二分处理要好很多
//这里放这个代码是让大家看浮点二分和整数二分的一些小区别

运行结果

边界问题

对于不用ans记录答案的整数二分

当mid可行，就在left~mid区间里面找（往小了找），否则就在mid+1~right之间找！

在二分查找的时候我所有的代码都是用这种方式写的（但是我没有详细介绍括号内的代码实现）

我在上方相关位置也有提示，这里来具体表述一下。

举个例子：

我现在要找升序数列中大于等于某个数key的最小位置。

check(mid)=true（if条件满足）：right=mid

check(mid)=false（if条件不满足）：left=mid+1
然后用新的区间不断重复即可

再举个例子：

我现在要找升序数列中小于等于某个数key的最大位置

check(mid)=true：left=mid

check(mid)=false：right=mid-1

但是此时要注意一个特殊情况，比如进行到某轮循环left=2，right=3，mid=5/2=2，此时测试的check(mid)为true，left和right将永远卡在2和3，显然mid永远无法达到right的位置进行检查，而且用来保存可行答案的是left，因此输出时也是left输出，虽然区间一直卡在2和3之间好像循环结束不了，但是亲测还是会输出2（即left的位置），万一right满足条件，那答案可不就是错了。

因此！我们取的中点要靠右，也就是 (left+right+1)/2，这样就能保证left和right不死循环。

但是这里就出现一个问题了left+right+1可能会越界耶~

这样真的超麻烦，所以咱就还是老老实实用记录答案的写法来解决整数二分比较好。

至于浮点二分left和right都行，因为在设置eps的时候已经为了保险多上了精度。

终于告一段落了，看到这里都辛苦了~

有错误欢迎指出~