前缀和差分（一维前缀和、差分，二维前缀和、差分）

前缀和

什么是前缀和？

前缀和可以理解为数组前n项的和。

这里给一个直观的一维数组a：1 2 3 4 5

那么它的前缀和就是新开一个数组使得数组中第n项等于原数组前n项之和，

即新数组b：1 3 6 10 15

前缀和的构造方法一目了然：b[i]=b[i-1]+a[i]

为什么前缀和要存在？（前缀和存在的意义）

前缀和是一种常用的、较为高效的预处理方式。

能够有效降低查询的时间复杂度。

前缀和怎么使用？（前缀和的应用）

前缀和在这里我只介绍一维前缀和和二维前缀和

一维前缀和

直接上题目了！！！

主要是这个前缀和代码实现实在没什么好讲的，着重在应用上。

P1115 最大子段和

测评网址：最大子段和 - 洛谷

题目描述

给出一个长度为 n 的序列 a，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 n。

第二行有 n 个整数，第 i 个整数表示序列的第 i 个数字 ai。

输出格式

输出一行一个整数表示答案。

输入输出样例

输入

7

2 -4 3 -1 2 -4 3

输出

4

说明/提示

样例 1 解释

选取 [3,5]子段 {3,−1,2}，其和为 4。

数据规模与约定

• 对于 40%的数据，保证n≤2×10^3。

• 对于 100%的数据，保证 1≤n≤2×10^5，−10^4≤ai≤10^4。

题目解析

求最大子段和我们可以用来化为求前缀和数列后项减前项差的最大值（这里的前项指的是前一项或前几项或不减）

代码实现

#include<stdio.h>
//更简便的算法往下翻翻（真的超级短小精悍的代码）
//后来写别的题从佬那里学过来的（本人也在学习的过程所以很多代码敲的不好）
//这个代码不想看就直接跳下边看（我放在这里也就是来表明一个算法的优化过程）
//直接学下边那个就行对你帮助应该更大些

int main() {
    int a[200001], b[200001] = { 0 }, c[200001] = { 0 }, n, ans;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    int i, j;
    for (int i = 0; i < n; i++) {
        if (i == 0)b[i] = a[i];
        else b[i] = b[i - 1] + a[i];
    }
    //b为a的前缀和（用b[i]=b[i-1]+a[i]）
    //避免用二层循环增加复杂度
    int min = 0;
    //min一定要初始化为0
    //用以计算第一项c
    for (int i = 0; i < n; i++) {
        c[i] = b[i] - min;
        min = (min < b[i]) ? min : b[i];
    }
    //c[i]为子段中包含第i项的最小子段和
    //min为b的第i-1项及之前最小的b项（最小前缀和）
    for (int i = 0; i < n; i++) {
        if (i == 0)ans = c[i];
        else {
            if (c[i] > ans)ans = c[i];
        }
    }//找出c中的最大项即为答案
    printf("%d\n", ans);
    return 0;
}

超级简短的在这！

int main() {
    int a[20001] = { 0 }, n, sum = 0, ans = -9999999;
    //ans一定要足够小，免得结果比初始化的ans小ans更新不了
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        if (sum < 0)sum = 0;
        //当sum还是正数，再加一个元素进来肯定比原来的大
        //如果sum为负数了，那重新算sum吧（从当前的a[i]开始）
        sum += a[i];
        if(sum > ans)ans = sum;
        //更新最大值（每加一次）
    }
    printf("%d", ans);
    return 0;
}

二维前缀和

以上我们的讨论均基于一维数组，然而当数组转化为2维数组时，它的前缀和是什么呢？

我们先来看下面这张图。

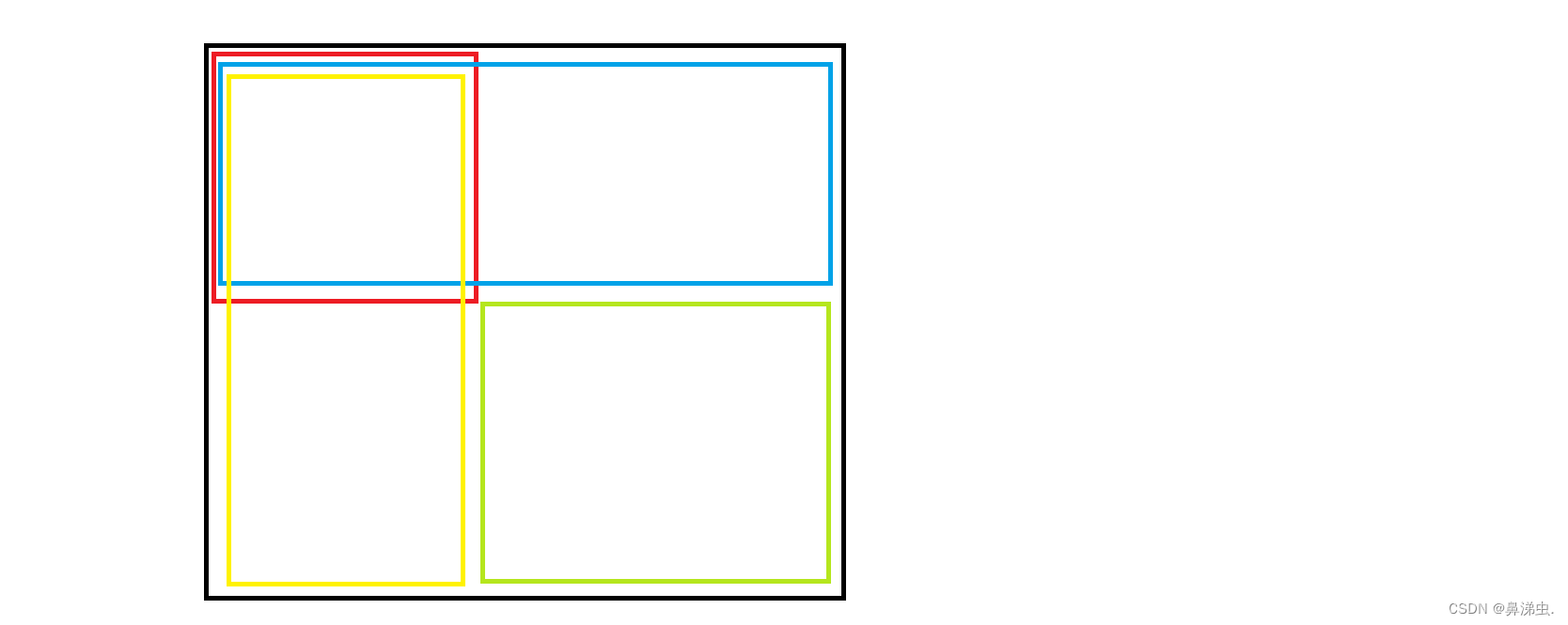
我们令黑色部分矩形面积为s[i][j]（前缀和），则有红色面积为s[i-1][j-1]（前缀和），蓝色面积为s[i-1][j]（前缀和），黄色面积为s[i][j-1]（前缀和），绿色面积为a[i][j]（原二维数组元素）。

显然我们可以知道，

黑色（面积）=蓝色+黄色+绿色-红色（多加了一次）

因此有s[i][j]=s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1]

于是我们就得到了如上的二维数组前缀和的通项公式。

好了，了解了原理，我们开始做题。

P1719 最大加权矩形

测评网址：最大加权矩形 - 洛谷

题目描述

为了更好的备战 NOIP2013，电脑组的几个女孩子 LYQ,ZSC,ZHQ 认为，我们不光需要机房，我们还需要运动，于是就决定找校长申请一块电脑组的课余运动场地，听说她们都是电脑组的高手，校长没有马上答应他们，而是先给她们出了一道数学题，并且告诉她们：你们能获得的运动场地的面积就是你们能找到的这个最大的数字。

校长先给他们一个 n×n 矩阵。要求矩阵中最大加权矩形，即矩阵的每一个元素都有一权值，权值定义在整数集上。从中找一矩形，矩形大小无限制，是其中包含的所有元素的和最大 。矩阵的每个元素属于 [−127,127] ,例如：

 0 –2 –7  0 
 9  2 –6  2
-4  1 –4  1 
-1  8  0 –2

在左下角：

9  2
-4  1
-1  8

和为 15。

几个女孩子有点犯难了，于是就找到了电脑组精打细算的 HZH，TZY 小朋友帮忙计算，但是遗憾的是他们的答案都不一样，涉及土地的事情我们可不能含糊，你能帮忙计算出校长所给的矩形中加权和最大的矩形吗？

输入格式

第一行：n，接下来是 n 行 n 列的矩阵。

输出格式

最大矩形（子矩阵）的和。

输入输出样例

输入

4

0 -2 -7 0

9 2 -6 2

-4 1 -4 1

-1 8 0 -2

输出

15

说明/提示

1≤n≤120

题目解析

显然这是一个矩阵元素和的问题，恰好与上方介绍的二维前缀和不谋而合，这里的矩阵和相当于s[i][j]，我们的目的就被抽象为求s[i][j]-s[i-1][j]-s[i][j-1]-s[i-1][j-1]+s[i-1][j-1]的最大值（如果不能反应过来，自行画图辅助理解，就会觉得非常easy了。

代码实现

#include<iostream>
using namespace std;
int main() {
    int n, a[128][128] = { 0 };
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            //这里i全部从1开始方便进行题目的对应不说
            //矩阵元素初始化为0以后对于运算的算式中一切与i-1和j-1相关的式子具有普适性
            //不必再单独处理什么i==0时怎么样怎么样
            //这样的写法也可以放入前面的一维前缀和代码里进行优化（就是多占了点空间）
            scanf("%d", &a[i][j]);//输入矩阵中元素的值
        }
    }
    int sum[128][128] = { 0 }, max = a[1][1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + a[i][j] - sum[i - 1][j - 1];
            //算出每个从第一行第一列元素累加到第i行第j列的元素之和sum[i][j]
            for (int p = 0; p < i; p++) {
                for (int q = 0; q < j; q++) {
                    if (max < sum[i][j] - sum[p][j] - sum[i][q] + sum[p][q])max = sum[i][j] - sum[p][j] - sum[i][q] + sum[p][q];
                    //找出第p+1行第q+1列元素累加到第i行第j列的矩阵元素的最大值（即所求值）
                }
            }
        }
    }
    printf("%d", max);
    return 0;
}

差分

什么是差分？

所谓差分，既然和前缀和放在同一篇文章下，差分显然也和前缀和有密不可分的关系。

我们再把上面的数组拿下来：1 2 3 4 5

设这个数列为a，数列a的前缀和数列1 3 6 10 15为b

则有b[i]=b[i-1]+a[i] ;

我们称数组b是数组a的前缀和数组。

而数组a就是数组b的差分数组。

即差分相当于前缀和的逆运算！！！

那么前缀和的构造我们使用b[i]=b[i-1]+a[i]，差分的构造又如何进行呢？

移项一下我们就可以知道a[i]=b[i]-b[i-1]

即差分数组的某项等于这一项减前一项的差

第一项就是第一项的值保持不动，因此这里同样可以用数组初始化为0，i从1开始的录入方式。

为什么差分要存在？（差分存在的意义）

差分的存在意义和前缀和相同，都是为了降低时间复杂度而生。

差分怎么使用？（差分的应用）

一维差分

先来一道很纯粹的一维差分题~

P3397 地毯

测评网址：地毯 - 洛谷

题目描述

在 n×n 的格子上有 m 个地毯。

给出这些地毯的信息，问每个点被多少个地毯覆盖。

输入格式

第一行，两个正整数 n,m。意义如题所述。

接下来 m 行，每行两个坐标 (x1​,y1​) 和 (x2​,y2​)，代表一块地毯，左上角是 (x1​,y1​)，右下角是 (x2​,y2​)。

输出格式

输出 n 行，每行 n 个正整数。

第 i 行第 j 列的正整数表示 (i,j) 这个格子被多少个地毯覆盖。

输入输出样例

输入

5 3
2 2 3 3
3 3 5 5
1 2 1 4

输出

0 1 1 1 0
0 1 1 0 0
0 1 2 1 1
0 0 1 1 1
0 0 1 1 1

说明/提示

样例解释

覆盖第一个地毯后：

覆盖第一、二个地毯后：

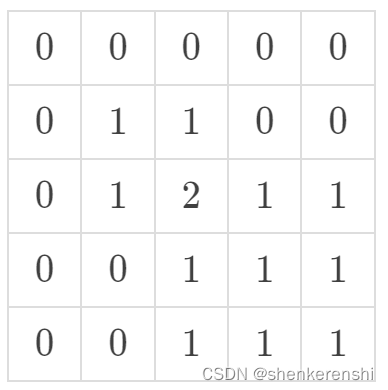
覆盖所有地毯后：

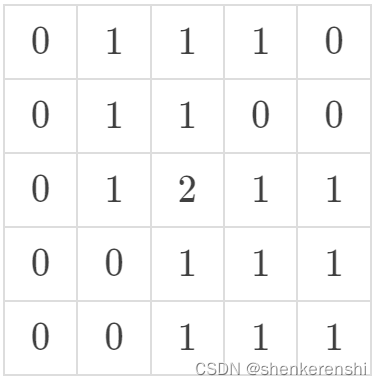
数据范围

对于 20% 的数据，有 n≤50，m≤100。

对于 100% 的数据，有 n,m≤1000。

题目解析

我们先通过暴力解法明白题目中的含义（事实上这道题的数据很水，暴力o(n^3)也能过）

懒得看代码就看第二个注释就明白了。

#include<iostream>
#include<cstring>
using namespace std;

int a[1002][1002];

int main() {
	int n, m;
	scanf("%d %d", &n, &m);
	int carp[5] = { 0 };//用以记录x1,y1,x2,y2
	for (int i = 0; i < m; i++) {
		for (int j = 1; j <= 4; j++)scanf("%d", &carp[j]);
		//从左上角行到右下角行（最小行数到最大行数）嵌套左上角列到右下角列（最小列数到最大列数）遍历使数值++
		for (int j = carp[1]; j <= carp[3]; j++) {
			for (int k = carp[2]; k <= carp[4]; k++) {
				a[j][k]++;
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (j < n)printf("%d ", a[i][j]);
			else printf("%d\n", a[i][j]);
		}
	}
	return 0;
}

显然o(n^3)的时间复杂度太高了，我们利用一维差分能够缩减时间复杂度到o(n^2)。

先对下列一维数组进行一些差分操作：

有以下1~10数组：

0 0 0 0 0 0 0 0 0 0

我想对3~6进行加一操作，那么我可以对3~6区间进行如下处理：

① 0 0 1 0 0 0 -1 0 0 0（对3和7分别赋值1和-1）

② 0 0 1 1 1 1 0 0 0 0（向后累加，即从前往后遍历每项等于该项值加上前项值——前缀和）

这样两步操作就可以完成我想进行的加一操作。

那么我们现在再推广到对二维数组进行差分操作：

假设我们要覆盖的矩阵范围是[(2,2),(5,5)]（左上角和右下角），可以对一个零矩阵进行以下赋值：

0 0 0 0 0 0
0 + 1 0 0 0 - 1
0 + 1 0 0 0 - 1
0 + 1 0 0 0 - 1
0 + 1 0 0 0 - 1
0 0 0 0 0 0

相当于对要赋值矩阵块的每一行都进行如一维数组那般的赋值，此后的操作也类似，对整个矩阵进行如一维数组般的向后累加即可。（对每一行进行一维前缀和）

值得注意的是：

这里的矩阵若本身有值（非零矩阵），不能直接在原有矩阵上进行一些+1和-1的赋值操作，这样是不对的！

需要新开一个进行操作的零矩阵（这里设为flag矩阵），而进行数次操作（如题设中的数块地毯），如第2块的地毯对第1块地毯赋值过的flag矩阵继续进行+1/-1操作（即使此时的flag矩阵非零）

总而言之，flag矩阵就是用于记录变化次数的矩阵，进行整体的前缀和后其在位置(i,j)上的数值即为进行一次或多次区域+1操作后位置(i,j)上的值变化，此时将原矩阵与flag矩阵相加即可得出结果。

类似我们也可以拓展到对矩阵区域进行其他操作，如区域+2，即把相应位置变为+2和-2，区域-1，即把相应位置变为-1和+1。

代码实现

int main() {
	int n, m;
	scanf("%d %d", &n, &m);
	int x1, y1, x2, y2;
	for (int i = 0; i < m; i++) {
		scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
		for (int j = x1; j <= x2; j++) {
			a[j][y1]++;//使地毯第一列全部+1
			a[j][y2 + 1]--;//使地毯最后一列的后一列全部-1
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			a[i][j] += a[i][j - 1];//进行向后累加操作（对整个矩阵）
			if (j != n)printf("%d ", a[i][j]);
			else if (j == n)printf("%d\n", a[i][j]);
		}
	}
	return 0;
}

二维差分

同一道题我们也可以用二维差分来解决。

我们先对二维差分进行一个一般的叙述。

二维差分有别于一维差分的好处就是，不必再对两列进行赋值，而只要对区域边界四角的四个单点值进行赋值即可进行对某个区域的整体加减某值。

其图解如下：

我们对一个5*5矩阵进行[(1,1),(3,3)]区域的赋值，对flag矩阵进行如下处理再进行二维前缀和，便可得到增值矩阵。

回到地毯那道题目，即对于题中所给的(x1,y1),(x2,y2)，对于每块地毯我们仅需对flag矩阵进行四角赋值，即：

flag[x1][y1] += 1；

flag[x1][y2+1] -= 1;

flag[x2+1][y1] -= 1;

flag[x2+1][y2+1] += 1;

进行m块地毯的赋值之后再对flag数组进行本文前面介绍的二维前缀和即可得到每个位置(i,j)所覆盖的地毯层数。

代码实现

#include<iostream>
#include<cstring>
using namespace std;
int a[1002][1002];
int sum[1002][1002];
int main() {
	int n, m;
	scanf("%d %d", &n, &m);
	for (int i = 0; i < m; i++) {
		int x1, y1, x2, y2;
		scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
        //四角赋值
		a[x1][y1]++; a[x1][y2 + 1]--; a[x2 + 1][y1]--; a[x2 + 1][y2 + 1]++;
	}
    //二维前缀和
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + a[i][j] - sum[i - 1][j - 1];
			printf("%d ", sum[i][j]);
		}
		printf("\n");
	}
	return 0;
}

这样得到的结果时间复杂度仍然是o(n^2)，有所改进的地方是进行标记时的时间复杂度由o(n)变化为了o(1)。

文章到这里就结束了，许久未更，只是今日清闲，看见去年三月份写的文章还未完成，心血来潮将其堪堪写完，如今再看先前写的代码觉得十分厌恶，果然每六个月返回看自己代码都会觉得嫌弃吗。

今天是19岁生日，了却这篇文章，日后估计也是忙，过去的算法学习早已告一段落，大概率是不会更了，这几篇基础算法就留给后来学习的人吧，归纳得也很详尽了，感谢各位的陪伴~