编译原理期末重点-个人总结——2 文法与语言

文法和语言

基本概念

语言⭐

由句子组成的集合，由一组记号所构成的集合。语言三个方面定义：

• 语法 – 各个记号间的组合规律
• 语义 – 各个记号的特定含义。（各个记号和记号所表示的对象之间的关系）
• 语用 --各个记号所出现的行为中，它们的来源、使用和影响。

文法⭐

简单来说就是语法的规则

假设我们设计一个语言，只允许写加法表达式，比如：

• 1 + 2
• 3 + 4 + 5

//E表达式  T基本项
//设计出的文法如下
E → E + T   
E → T     
T → 数字   //→ 的意思是“可以写成”
    
//设计出的规则：一个表达式可以是一个表达式加一个数字，或直接是数字

符号

符号是 字母表中的元素

例如：汉语的字母表中包括汉字、数字及标点 符号等

符号串

由字母表中的符号组成的任何有穷序列

串的头尾

符号串的长度

符号串的长度记为|s|，空字符串长度为0

方幂

符号串x自身连接n次得到的符号串

闭包

文法形式定义

规则

α→β或α∷=β

• α称为规则的左部(或生成式的左部)
• β称为规则的右部(或生成式的右部)

文法定义⭐

文法习惯上只将产生式写出，用尖括号括起的是非终结符，否则为终结符

推导⭐

α→β是文法G产生式 v=γαδ, w = γβδ

则 **v（应用规则α→β）直接产生w **，称 w直接归约到v

句型与句子⭐

语言⭐

文法的等价

若L（G1）=L（G2），则称文法G1和G2是等价的。

文法类型⭐

0型文法（无约束文法/短语文法）

对于产生式α→β，只要α不是空串即可。

1型文法（上下文有关文法）

产生式的形式必须是αAβ→αγβ ，γ是非空的，简单说，在将A替换成γ时，需要考虑A周围的上下文（即α和β） 简单判断：左边数<=右边

**2型文法（上下文无关文法）**⭐

要求所有的产生式形式都是A→γ ，γ 是任意字符串，替换A为γ时不考虑其周围环境

**3型文法（正则文法）**⭐

进一步限制产生式格式，分为右线性文法和左线性文法

• 右线性文法的产生式形式为A→aB或A→a
• 左线性文法的产生式形式为A→Ba或A→a

其中A和B是非终结符，a是终结符

例子

G[S]： 文法定义如下：
S → aSBE
S → aBE
EB → BE
aB → ab
bB → bb
bE → be
eE → ee

首先分析出S是终结符，其余为非终结符，然后判断是否为正则文法（3型） ❌

• S → aSBE ❌（右边有多个非终结符，不是右线性）
• S → aBE ❌（同上）
• EB → BE ❌（左边有两个非终结符，不符合正则文法）
• aB → ab ❌（左边有一个终结符和一个非终结符，不是 A → a 或 A → aB）

判断是否为2型文法（上下文无关文法） ❌

• S → aSBE ✅
• S → aBE ✅
• EB → BE ❌（左边是两个非终结符 EB，不是单个非终结符）
• aB → ab ❌（左边是终结符+非终结符，不是单个非终结符）
• ……其他也类似，有多个左边不是单一非终结符的情况

判断是否为上下文有关文法（1型）✅ 简单判断：左边数<=右边

上下文无关法及其语法树⭐

上下文无关文法有足够的能力描述现今程序设计语言的语法结构。 无特殊说明，“文法”均指上下文无关文法

例子： G[S]: S→aAS A→SbA A→SS S→a A→ba 能得到句型aabbaa？

语法树

从左到右读出树的叶子标记，所得的句型为推导树的结果。aabbaa 所以正确，可以看到用语法树做很快

语法树怎么画？

核心就是通过通过下面最左推导 或 最右推导 的分析过程 来构建语法树

最右推导

也被称为规范推导，推导出来的规范句型。总是选择当前句型中最右边的非终结符进行展开。

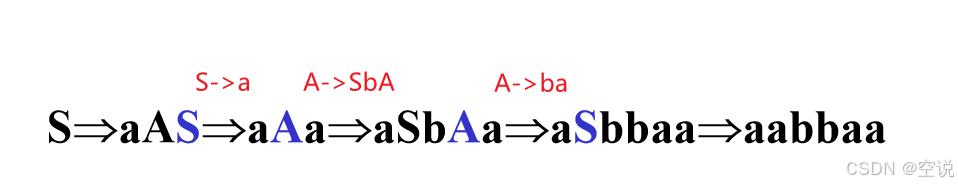
最左推导

总是选择当前句型中最左边的非终结符进行展开。

文法的二义性⭐

一个句型是否对应唯一的一棵语法树？ 不一定，得看是否有二义性

文法二义性：

若一个文法存在某个句子对应两棵不同的语法树，则称这个文法是二义的。

产生某上下文无关语言的每一个文法都是二义的

如果文法G 是无二义的，则它的任何句子最左推导和最右推导对应的语法树一定相同

二义文法改造为无二义文法

//原始二义文法 G[E]
E → E + E
E → E * E
E → (E)
E → id
它可以有两种不同的解析树，一种是先执行加法（id + (id * id)），另一种是先执行乘法（(id + id) * id）。这表明该文法是二义的。
    
//改造后的无二义文法
引入额外的非终结符来区分不同优先级的操作。例如，我们用 T 表示项（通过加法连接的部分），用 F 表示因子（通过乘法连接的部分）
E  → T | E + T
T  → F | T * F
F  → (E) | id    

1. 从 E 开始：
   • 根据规则 E → T | E + T，首先尝试匹配最左边的 id，这意味着我们要应用 E → T。
2. 展开 T：
   • 对于第一个 id，使用 T → F 和 F → id 得到第一个因子。
   • 接下来遇到 +，按照 E → E + T 继续推导，意味着我们需要继续处理右边的部分 id * id。
3. 处理右侧的 T：
   • 右侧的第一个 id 同样遵循 T → F 和 F → id。
   • 遇到 *，应用 T → T * F，进一步展开右边的 id 使用 F → id。

使用最左推导 或最右推导 发现推导过程不一样，所以语法树不一样

句型分析

句型分析就是识别一个符号串是否为某文法的句型，是某个推导的构造过程。

把完成句型分析的程序称为分析程序或识别程序。分析算法又称识别算法。

分析算法可分为

• 自上而下分析法：从文法的开始符号出发，反复使用各种产生式，寻找与输入符号匹配的推导。
• 自下而上分析法：从输入符号串开始，逐步进行归约，直至归约到文法的开始符号。

例子

//这是一个简单的上下文无关文法
S → aAB
A → bB
B → c | d
//目标：判断字符串 abdc 是否是该文法的一个句型    

自上而下分析法 ：从上往下一步步分析

使用 S → aAB，匹配第一个字符 a，成功！

使用A → bB，匹配第二个字符 b，成功！ S → abBB

使用B → d，匹配第三个字符 d，成功！ S → abdB

使用B → c，匹配第四个字符 d，成功！ S → abdc

自下而上分析法 从最下面（字符串）开始，一层层往上拆，看能不能回到顶部那块S

使用一个栈来模拟归约过程

• 移进（shift）：把当前字符压入栈中
• 归约（reduce）：如果栈顶的符号串能匹配某条产生式的右边，就替换成左边的非终结符

栈	输入	动作
	a b d c #	初始状态
a	b d c #	移进 a
ab （b可以通过A → b这个产生式替换成A）	d c #	移进 b
aA	d c #	归约 b → A
aAd	c #	移进 d
aAB	c #	归约 d → B
aABc	#	移进 c
aAB	#	归约 c → B
S	#	归约 aAB → S
		成功归约到 S

化简文法

例：G[S]

1. S→Be
2. B→Ce
3. B→Af
4. A→Ae
5. A→e
6. C→Cf
7. D→f
8. A→A

逐步替换产生式中的非终结符，看看是否能最终归约为终结符串，核心就是找 非终结符=>终结符

非终结符	能否推出终结符？	理由
A	✅ 是	有 A → e 和 A → Ae，能生成任意多个 e
D	✅ 是	D → f
B	❓ 暂不确定	因为它依赖于 A 或 C
C	❌ 否	C → Cf 是无限递归，永远不能变成终结符
S	❓ 暂不确定	它依赖于 B

B → Af：A 可以推出终结符 ⇒ B 可以推出终结符
B → Ce：C 不能推出终结符 ⇒ 这条规则无效
S → Be：B 可以推出终结符 ⇒ S 也可以推出终结符
    
有用的非终结符集合是：{A, B, S}    

• S → Be ✅ （S 是有用的）
• B → Ce ❌（C 是无用的）
• B → Af ✅（B 是有用的）
• A → Ae ✅（A 是有用的）
• A → e ✅（A 是有用的）
• D → f ❌（D 虽然有用，但没有被其他规则引用，也无法从 S 推导出来）
• C → Cf ❌（C 是无用的）
• A → A ❌（虽然 A 是有用的，但这条规则是空循环）

//最终保留下来的产生式
S → Be  
B → Af  
A → Ae  
A → e