[TJOI2013] 松鼠聚会题解

Tag : 曼哈顿距离 , 切比雪夫距离

[TJOI2013]松鼠聚会

• 对于一个点，一个点到周围的八个点距离为 1，即为 切比雪夫距离 的定义距离

• 易得两点之间距离为 $max(|x2-x1|,|y2-y1|)$

• 曼哈顿距离 ： $|x2-x1|+|y2-y1|$

• 两者之间可以相互转换

• 此题要我们求一些点到点的 切比雪夫距离 之和，带有 $max$ 的加减不是很好做，化为 曼哈顿距离 ,即化为绝对值的加减会好做许多

---

• 将 切比雪夫距离 转换为 曼哈顿距离：

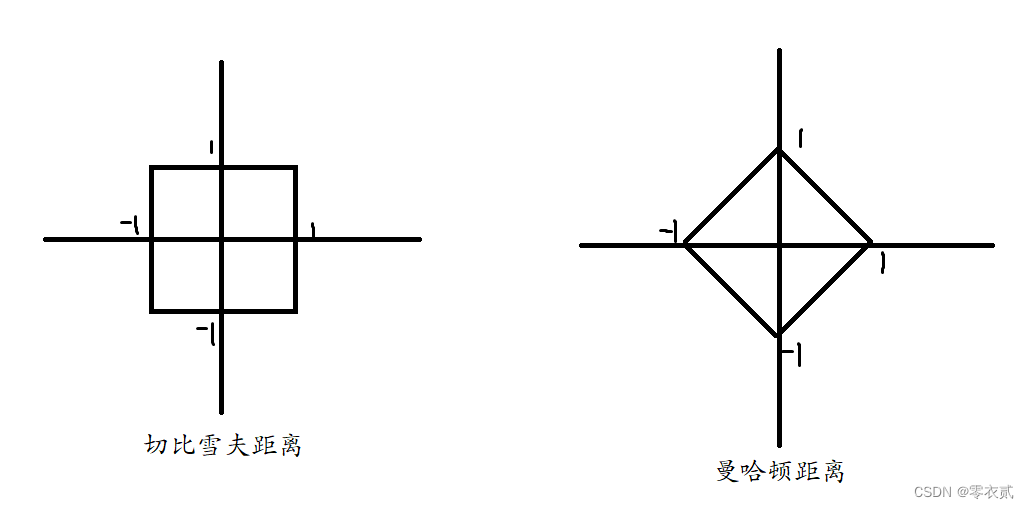
• 在切比雪夫距离 下距离原点 1个单位的点会形成一个如图所示的正方形

• 在曼哈顿距离 下距离原点1个单位的点会形成一个如图所示的倾斜的正方形

• 转移公式：

• 切比雪夫 转 曼哈顿

  $(x,y)\to (\frac{x+y}{2},\frac{x-y}{2})$

• 曼哈顿 转 切比雪夫

  $(x,y)\to (x+y,x-y)$

---

• 回到题目，我们应该先将坐标按上文所述的公式转化为在 曼哈顿距离 下的坐标

• 假设聚会地点为 $i$ 号点

• 最终答案即为 $|x_1-x_i|+...+|x_i-x_i|+...+|x_n-x_i|$
  加上 $|y_1-y_i|+...+|y_i-y_i|+...+|y_n-y_i|$

• 如果我们按序列 $x$ 排序，那么对于前 $i$ 项, $x_1...x_i\le x_i$ ,
  和即为 $i\ast x_i-(x_1+...+x_i)$ ，用前缀和表示即为 $i\ast x_i-su{m}_i$

  而对于第 $i+1$ 到 $n$ 个数，和即为 $(x_{i+1}+...+x_n)-(n-i)\ast x_i$，用前缀和表示即为 $su{m}_n-su{m}_i-(n-i)\ast x_i$

• 另一方面，我们将序列按 $y$ 排序，二分找出 $x_i$ 对应的 $y_i$ 在按 $y$ 排序后的位置 $i$ ，同理加上 $i\ast y_i-su{m}_i$ 以及 $su{m}_n-su{m}_i-(n-i)\ast y_i$

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+5;
int n;
struct Node{
	double x,y;
}a[MAXN],b[MAXN],c[MAXN],pre[MAXN];
void build()
{
	for(int i=1;i<=n;i++)
	{
		b[i].x=(a[i].x+a[i].y)/2;
		b[i].y=(a[i].x-a[i].y)/2;
		c[i] = b[i];
	}
}
bool cmp1(Node p,Node q){return p.x<q.x;}
bool cmp2(Node p,Node q){return p.y<q.y;}
void Pre()
{
	for(int i=1;i<=n;i++)
	{
		pre[i].x = pre[i-1].x + b[i].x;
		pre[i].y = pre[i-1].y + c[i].y;
	}
}
int search(double target)
{
	int l=1,mid,r=n;
	while(l<=r-5)
	{
		mid=(l+r)>>1;
		if(c[mid].y <= target) l=mid;
		else r=mid;
	}
	for(int i=l;i<=r;i++)
		if(c[i].y==target) return i;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i].x>>a[i].y;
	
	build();
	
	sort(b+1,b+n+1,cmp1);
	sort(c+1,c+n+1,cmp2);
	
	Pre();

	double ans=1e18+7;
	for(int i=1;i<=n;i++)
	{
		double res=0;
		res += b[i].x * i - pre[i].x;
		res += (pre[n].x - pre[i].x) - b[i].x * (n-i);
		
		int pos = search (b[i].y);
		res += c[pos].y * pos - pre[pos].y;
		res += (pre[n].y - pre[pos].y) - c[pos].y * (n-pos);
		ans = min(ans,res);
	}
	
	cout<<(int)ans;
}