binary_search_tree的介绍与实现（二叉搜索树精美图示详解哦）

引言

在C语言部分，我们已经认识了树与二叉树的结构：
戳我看树与二叉树介绍
并且了解了二叉树顺序结构带来的一些应用，即在堆中的应用：
戳我看堆详解哦
戳我看优先级队列详解

但是二叉树的链式结构仿佛在数据处理方面并没有什么突出的表现，在对一个没有什么特征的二叉树进行增删查改是没有什么意义的。但是如果链式的二叉树具有了一些特性，就会使它在数据处理上的效率出现质的提升。

二叉搜索树，顾名思义，在搜索方面的表现很突出：
之前我们了解到的效率很高的搜索算法就是二分查找算法，在二分查找算法下，搜索的时间复杂度可以达到 O(logN)。但是二分查找有一个很大的限制条件，即它必须要求数据有序；
但是对于二叉搜索树而言，在建立二叉搜索树结构后，就可以实现查找效率为 O(logN)。

二叉搜索树的介绍

二叉搜索树即在二叉树的基础上满足：
对于任何一个根结点，若左子树不为空，它的左子树的值全部小于根节点；若右子树不为空，右子树的值全部大于根节点。这也就意味着，如果我们中序遍历一个二叉搜索树，得到的一定是一个递增序列：

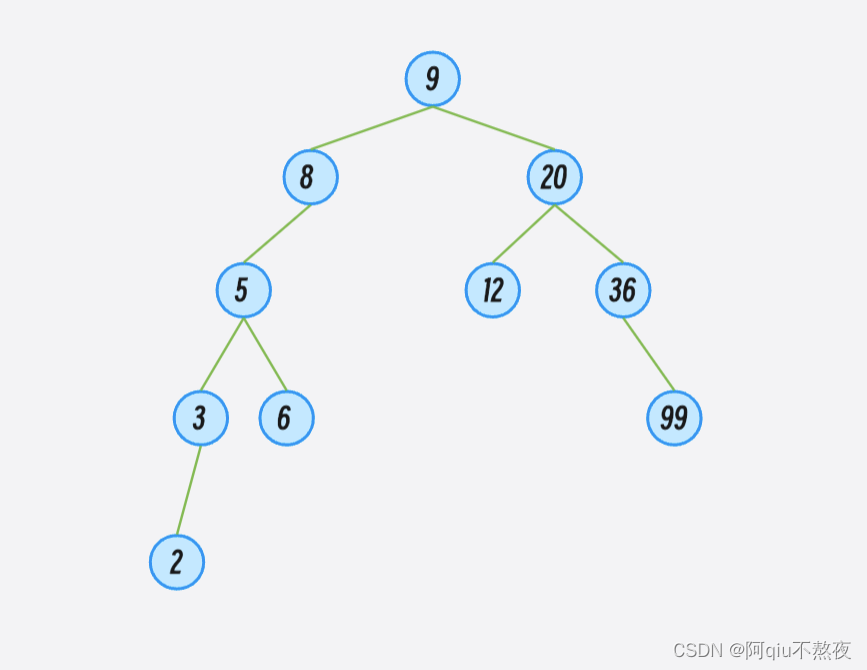
在这样的搜索二叉树中，如果我们想要查找某个值target，我们只需要从根结点开始，若当前结点的值大于target向左找，小于target向右找。就可以以很高的效率找到target：

但是，同样是这样的10个数据，根据插入的顺序不同，就会有不同形状的二叉搜索树。在最坏的情况下，二叉搜索树的形状就与单链表类似：

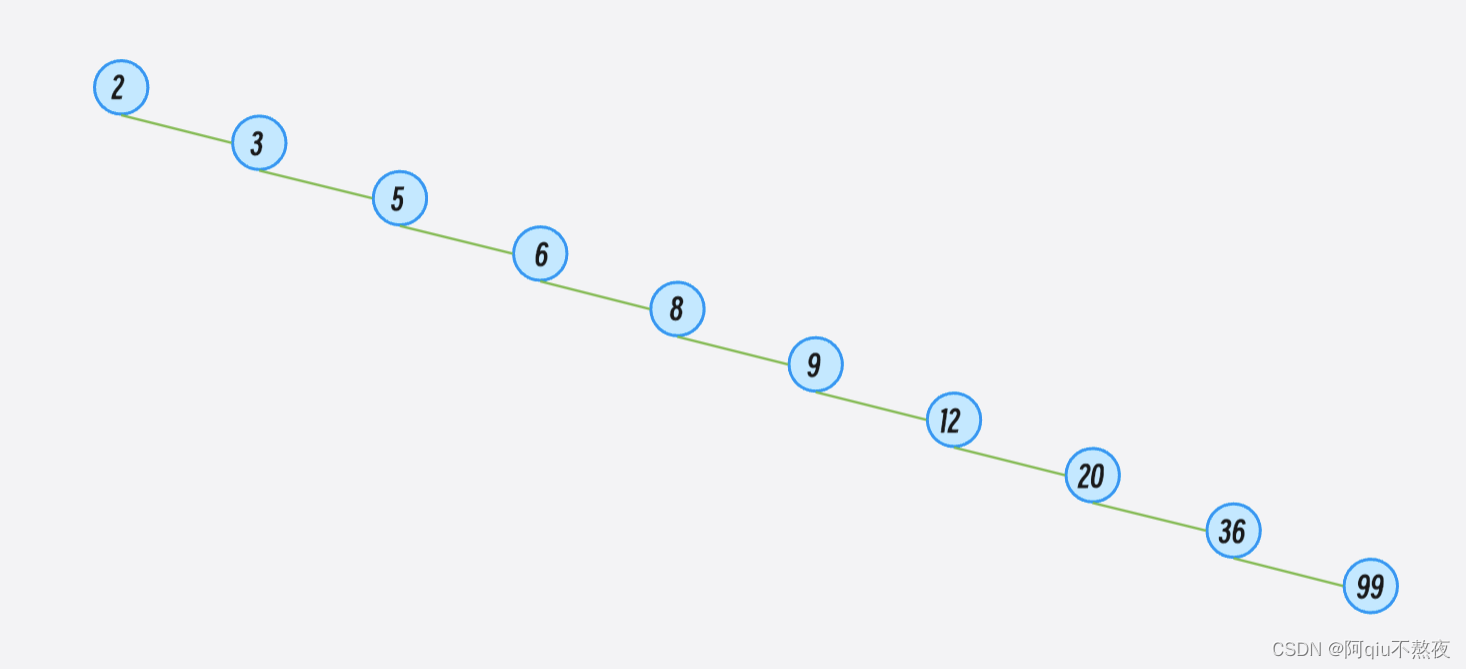
在这种情况中，搜索的时间复杂度就变成了O(N)（在下一篇文章中介绍到的平衡二叉树，就可以解决这样的问题）

二叉搜索树的实现

在了解了二叉搜索树后，就来详细介绍其实现：

框架

在二叉树的链式结构中，父结点有指向左右孩子结点的指针，依次向下结构相同。即树形结构具有很好的递归特性，所以在此次实现中选择使用递归的方式（函数名中的R表示递归版本实现）；
当然，为防止命名冲突，将实现放在我们的命名空间qqq中。

二叉搜索树BSTreeR是一个类模板，这样就可以支持二叉搜索书中存储各种数据。它的成员变量为根结点的指针：

	template<class K>
	class BSTreeR
	{
	protected:
		Node* _root; //Node 即 BSTreeNodeR<K> 的重命名
	};

二叉搜索树的结点类BSTreeNodeR当然也是一个类模板：
在结点类中有当前结点的数据与左右孩子结点的指针。在构造函数中对数据进行初始化，并且将左右孩子结点指针置空即可（由于在对树进行操作时，需要经常访问左右结点与数据，所以这个结点类直接使用struct来定义）：

	template<class K>
	struct BSTreeNodeR 
	{
		BSTreeNodeR<K>* _left;
		BSTreeNodeR<K>* _right;
		K _key;

		BSTreeNodeR(const K& key)
			: _key(key)
			, _left(nullptr)
			, _right(nullptr)
		{}
	};

另外，要想递归的实现二叉搜索树的增删查改，那么这个接口的参数中一定是有根结点指针的。但是根结点指针是一个私有的成员变量，所以我们在类外是不能调用这些递归的函数进行增删查改的。
所以我们选择将递归调用的函数（瓤）用另一个对外的接口（壳）包起来，我们在类外调用壳接口时，在壳中调用递归函数就可以解决不能访问私有成员变量的问题了（以InsertR为例）：

	template<class K>
	class BSTreeR
	{
	public:
		typedef BSTreeNodeR<K> Node;
	public:
		//壳接口
		bool InsertR(const K& key)
		{
			return _InsertR(_root, key);
		}
	protected:
		//递归函数
		bool _InsertR(Node*& root, const K& key);
        //树根节点指针
		Node* _root;
	};

默认成员函数

构造

对于构造函数，我们实现无参构造与拷贝构造：
无参构造没有什么说的，在构造函数**初始化列表中将根结点指针初始化为nullptr**即可：

	BSTreeR()
		: _root(nullptr)
	{}

拷贝构造就需要逐一使用原树中的结点去对新树的结点进行递归赋值：
在壳接口BSTreeR()中去调用递归函数_constructor():

	BSTreeR(const BSTreeR<K>& ctree)
	{
		_constructor(_root, ctree._root);
	}

_constructor()有两个参数，即原树的根结点指针croot与新树的根节点指针root的引用：

• 在函数中：首先判断原树的指针croot是否为空，若为空说明这给条分支已经拷贝完毕，返回给上一层去另外的分支拷贝；
• 若croot不为空，就使用原树结点中的数据来new一个结点；
• 然后使root指向新创建出的结点（由于root是根结点的引用，在该栈帧中进行修改同时也修改了上层调用的数据，即在这一步中就实现了将这个新结点与其父节点进行链接）；
• 然后两次递归调用，拷贝当前结点地两个子结点：

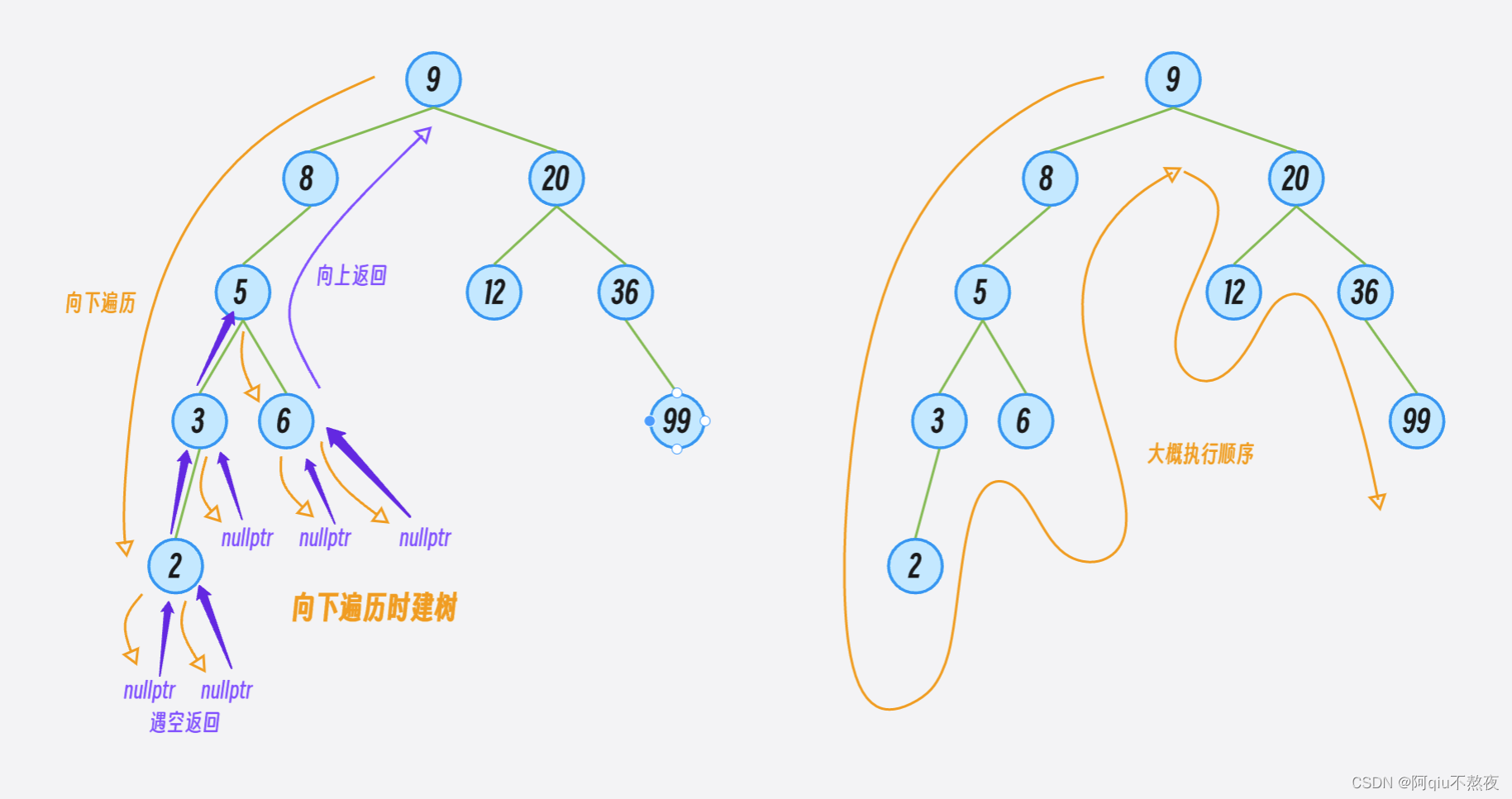
	void _constructor(Node*& root, Node* croot)
	{
		if (croot == nullptr)
			return;

		Node* newnode = new Node(croot->_key);
		root = newnode;
		_constructor(root->_left, croot->_left);
		_constructor(root->_right, croot->_right);
	}

析构

析构函数中，我们需要逐一释放每一个结点：
使用壳接口~BSTreeR()调用递归函数_destructor()：

	~BSTreeR()
	{
		_destructor(_root);
	}

_destructor的参数为根结点指针的引用。在析构时，如果先析构了当前结点，就不能再访问其左右结点，也就不能再继续析构下去了，所以这里使用的是后序遍历地析构方式，先析构其左右结点，再析构根结点：

• 在函数中：首先判断root是否为空，为空说明这条分支已经走到底，向上一层返回；
• 这里执行的是后序遍历，当不为空时，继续向下访问去析构左子树；
• 左子树析构完后向上返回，再继续向下访问去析构右子树；
• 右子树析构完后向上返回，才可以析构当前结点，即要析构当前结点，要么当前结点左右子树都为空，要么当前结点左右子树都已经被析构完了：

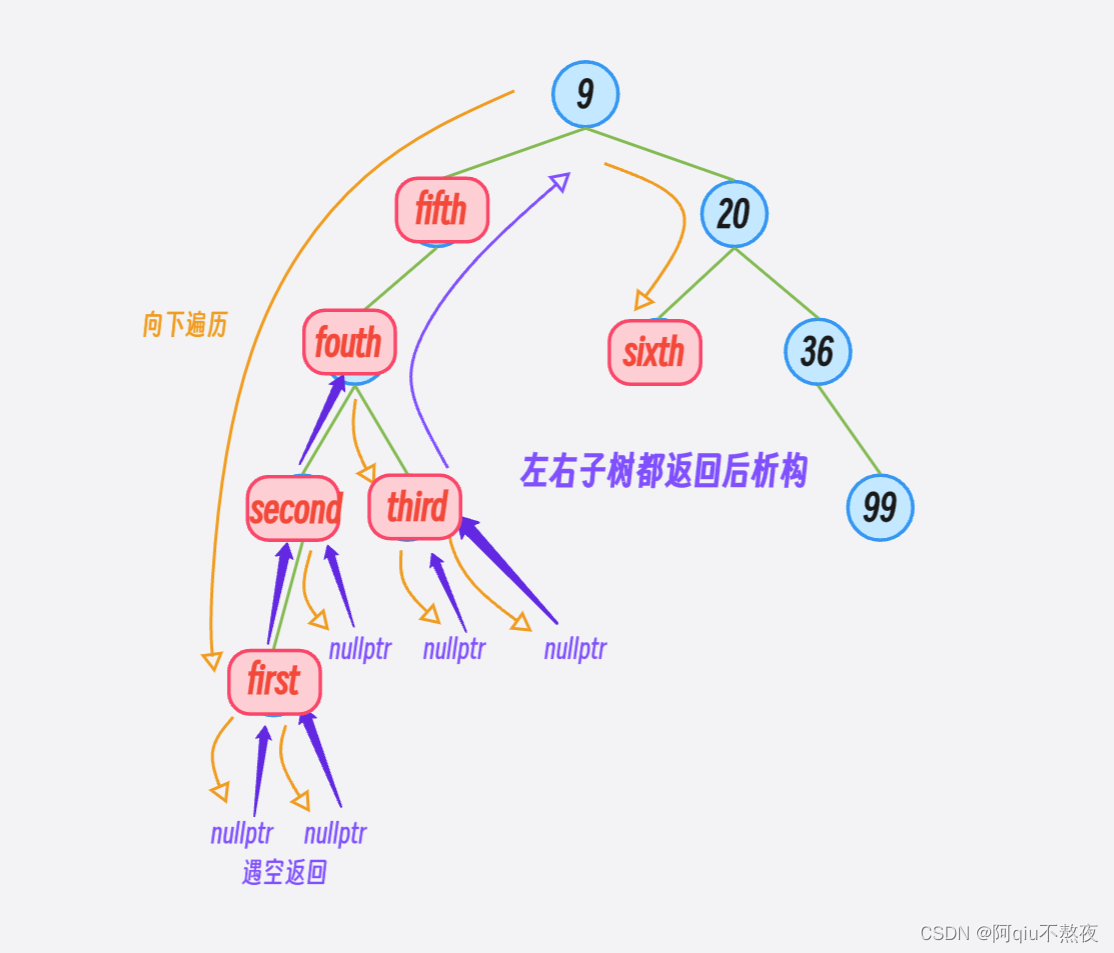
	void _destructor(Node*& root)
	{
		if (root == nullptr)
			return;

		_destructor(root->_left);
		_destructor(root->_right);
		delete root;
		root = nullptr;
	}

赋值重载

赋值重载，直接使用现代写法：

• 使用值传递，传参时生成一个临时对象ctree；
• 然后在函数中将当前对象的根结点指针与临时对象的根结点指针互换；
• 然后直接返回*this即可（被换值的临时对象在函数栈帧销毁时会自动析构，不用我们处理）：

	BSTreeR<K>& operator=(BSTreeR<K> ctree)
	{
		swap(_root, ctree._root);
		return *this;
	}

InsertR（插入）

在树中插入元素时，首先需要递归找到插入位置，然后进行链接。
当然，我们使用一个壳接口InsertR，其中调用递归函数_InsertR：

	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}

_InsertR有两个参数，即根结点指针的引用与要插入的元素。返回值为bool

在向下递归找正确位置的过程中：

• 若新数据小于当前结点的数据，向左边递归；
• 若新数据大于当前结点的数据，向右边递归；
• 若新数据等于当前结点的数据，说明这个数据已经存在，不能再插入，返回false；

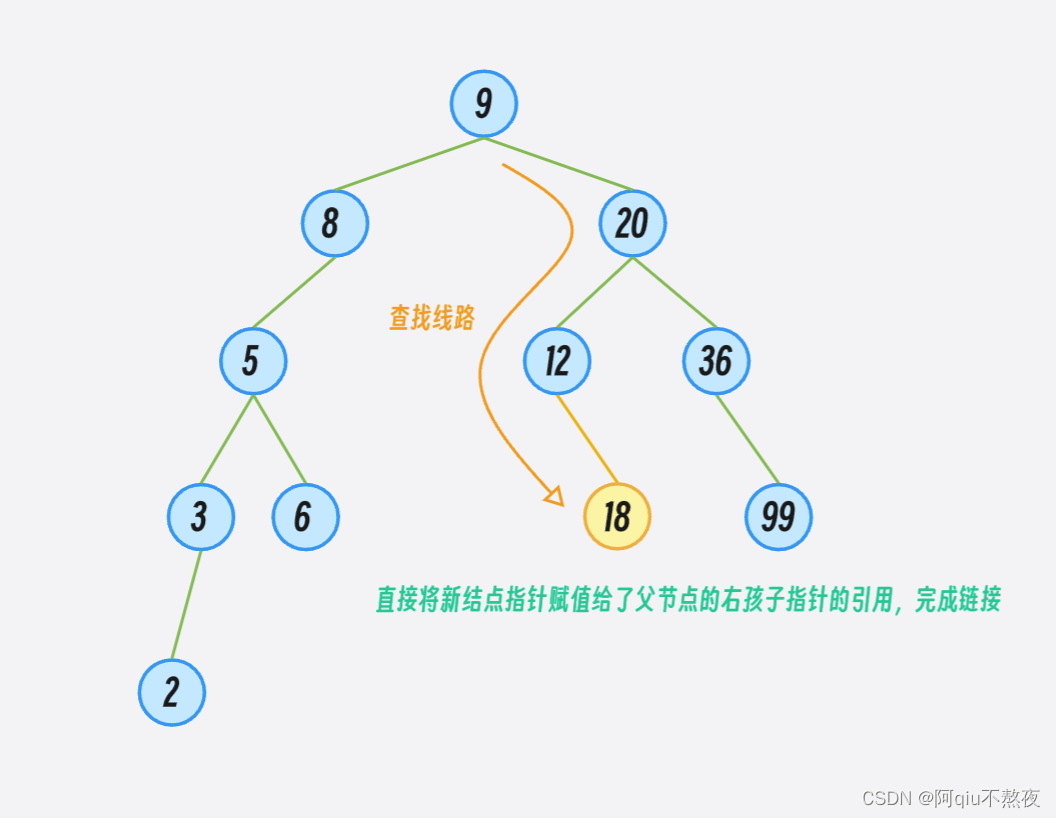
当向下遍历到树底时，即root == nullptr时，说明当前的位置就是插入位置，将新结点与上层结点链接即可。
但是这里存在着一个问题：即当前结点并不清楚自己是上层结点的左结点还是右结点。如果要在递归遍历时同时记录父结点，在不确定时与父节点重新比较一遍，这样就太麻烦了。
根节点指针的引用传参就完美的解决了这个问题：我们只需要让这个引用指向新结点即可。如果上层传参的是左孩子指针的引用，就能直接使左孩子指针指向新结点，传参右孩子指针的引用亦然：

	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			Node* newnode = new Node(key);
			root = newnode;
			return true;
		}

		if (key < root->_key)
		{
			return _InsertR(root->_left, key);
		}
		else if (key > root->_key)
		{
			return _InsertR(root->_right, key);
		}
		else
		{
			cout << "The key has existed" << endl;
			return false;
		}
	}

EraseR（删除）

删除的实现在二叉搜索树中是最复杂的一部分，其中有各种繁琐的情况，接下来就来一一分析解决：

先来简单的介绍一下删除的思路：

• 要在二叉搜索树中删除一个数据，我们首先要找到该数据的结点，然后才能将这个目标结点删除；
• 对于只有一个子树的目标结点而言，我们只需要将它的那个子树托管给它的父节点（若该数据小于其父结点，则其左右子树数据都小于其父结点，反之则都大于其父结点），然后直接释放它即可（这类似于单链表的删除）；
• 但是，如果这个目标结点有左右子树，那么就不能直接进行托管了，解决方案是：
  先将目标结点的数据于其左子树中的最大结点的数据进行交换（右树最小也可行，这里不进行介绍），这个左子树的最大结点一定只有一个左子树，或者没有孩子结点；
  然后按照上面的只有单孩子的思路进行删除即可：
  （这里将各个情况都进行图示）

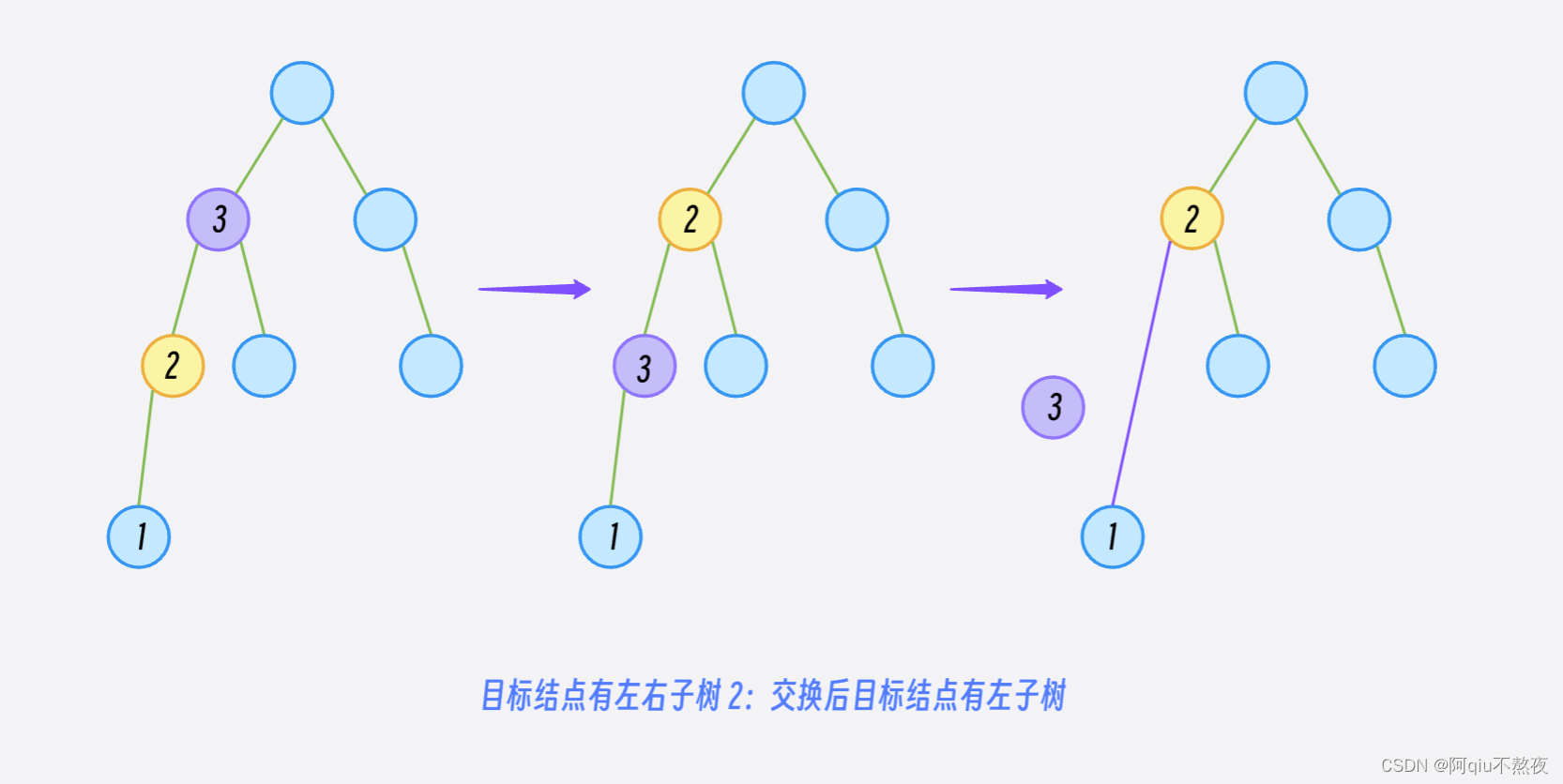
不可能有第四种情况了！

在写代码时，递归的方式其实要比非递归的方式要简便一些，虽然思路是一模一样的。

不必多说，在壳接口EraseR中调用递归函数_EraseR：

	bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}

_EraseR有两个参数，即根结点指针的引用与要删除的数据，返回值类型为bool；

在_EraseR函数中，首先递归寻找要删除的数据（若目标数据小于当前结点，向子树递归，反之向右递归），如果root == nullptr 就说明找到底都没有要删除的那个数据，返回false即可：

•   //递归找到要删的结点
    if (root == nullptr)
    {
    	cout << "The key does not exist" << endl;
    	return false;
    }
    	
    if (key < root->_key)
    {
    	return _EraseR(root->_left, key);
    }
    else if (key > root->_key)
    {
    	return _EraseR(root->_right, key);
    }
    else //找到
    {}
  

当找到要删除的元素后，判断这个目标结点的子树情况：

• 若目标结点只有左子树，将root->_right赋值给root后（前面提到过，这里的root是上层子结点指针的引用，所以这样的赋值可以直接完成链接），delete 掉root即可。但是如果在赋值后delete，释放掉的就是本来的root->right，如果在赋值前delete，之后就无法进行赋值，所以这里先用临时变量deltemp来存原来的root，在链接完成后释放deltemp即可（目标结点只有右子树情况与之相反）：

•     if (root->_left == nullptr) //左为空
    	{
    		Node* deltemp = root;
    		root = root->_right;
    		delete deltemp;
  
    		return true;
    	}
    	else if (root->_right == nullptr) //右为空
    	{
    		Node* deltemp = root;
    		root = root->_left;
    		delete deltemp;
  
    		return true;
    	}
  

• 若目标结点有左右子树，首先循环寻找左子树种的最大结点；
• 然后将最大结点的值与目标结点交换，这样要删除的目标结点就满足前面的情况了；
• 最后再递归调用一下_EraseR，参数就传交换后的目标结点，即之前的左树最大结点即可。这样就可以直接完成删除：

•   	else//有两个个孩子时，找左树中的最大元素，交换后再调该函数
    	{
    		Node*& leftMax = root->_left;
    		while (leftMax->_right) //循环找左最大
    		{
    			leftMax = leftMax->_right;
    		}
    		std::swap(leftMax->_key, root->_key);//交换值
  
    		return _EraseR(leftMax, key);
    	}
  

总体代码：

	bool _EraseR(Node*& root, const K& key)
	{
		//递归找到要删的结点
		if (root == nullptr)
		{
			cout << "The key does not exist" << endl;
			return false;
		}
			
		if (key < root->_key)
		{
			return _EraseR(root->_left, key);
		}
		else if (key > root->_key)
		{
			return _EraseR(root->_right, key);
		}
		else //找到
		{
			if (root->_left == nullptr) //左为空
			{
				Node* deltemp = root;
				root = root->_right;
				delete deltemp;

				return true;
			}
			else if (root->_right == nullptr) //右为空
			{
				Node* deltemp = root;
				root = root->_left;
				delete deltemp;

				return true;
			}
			else//有两个个孩子时，找左树中的最大元素，交换后再调该函数
			{
				Node*& leftMax = root->_left;
				while (leftMax->_right)
				{
					leftMax = leftMax->_right;
				}
				std::swap(leftMax->_key, root->_key);//交换值

				return _EraseR(leftMax, key);
			}
		}
	}

在这里简单介绍一下非递归的实现方式复杂在哪里了：
首先在找目标结点时，就需要一个辅助指针parentnode，来描述当前结点的父结点；
然后在只有一个子树或无子树的情况种，要判断目标结点与其父节点的大小，来决定要托管给父结点的哪个子树；
另外在寻找左子树的最大结点时，需要三个变量同时移动：一个变量leftmax描述左子树最大结点、一个变量maxparent描述这个最大结点的父节点、一个变量temp做临时变量；
最后对于要删除的目标结点究竟是无子节树点还是只有左子树的情况要进行判断：
（这里放一段非递归实现的代码，供大家参考）

		//非递归实现的erase
		bool Erase(const K& key)
		{
			Node* parentnode = _root;
			Node* cur = _root;

			while (cur)//找cur
			{
				if (key > cur->_key)
				{
					parentnode = cur;
					cur = parentnode->_right;
				}
				else if (key < cur->_key)
				{
					parentnode = cur;
					cur = parentnode->_left;
				}
				else
				{
					break;
				}
			}
			if (cur == nullptr)
			{
				cout << "The key does not exist" << endl;
				return false;
			}

			//要删除的结点只有一个孩子，将其孩子直接给其父亲
			//要删除的结点有左右孩子，用左子树中最大的元素替代它后，将左子树的元素删除。
			//若替代后，原左子树的最大结点存在左孩子，将其左孩子给其父亲
			if (cur->_left == nullptr && cur->_right == nullptr)
			{
				if (parentnode == cur)
				{
					_root = nullptr;
				}
				else if (cur->_key > parentnode->_key)
				{
					parentnode->_right = nullptr;
					delete cur;
				}
				else
				{
					parentnode->_left = nullptr;
					delete cur;
				}
			}
			else if (cur->_left == nullptr && cur->_right != nullptr)
			{
				if (parentnode == cur)
				{
					_root = cur->_right;
				}
				else if (cur->_key > parentnode->_key)
				{
					parentnode->_right = cur->_right;
					delete cur;
				}
				else
				{
					parentnode->_left = cur->_right;
					delete cur;
				}
			}
			else if (cur->_left != nullptr && cur->_right == nullptr)
			{
				if (parentnode == cur)
				{
					_root = cur->_left;
				}
				else if (cur->_key > parentnode->_key)
				{
					parentnode->_right = cur->_left;
					delete cur;
				}
				else
				{
					parentnode->_left = cur->_left;
					delete cur;
				}
			}
			else //左右孩子均不为空
			{
				//找左子树中的最大元素
				Node* maxparent = cur;
				Node* leftmax = maxparent->_left;
				Node* temp = leftmax->_right;
				while (temp)
				{
					maxparent = leftmax;
					leftmax = temp;
					temp = temp->_right;
				}

				std::swap(cur->_key, leftmax->_key);

				if (leftmax == maxparent->_left) //只有在这种情况下，才需要将最大值的左树（只可能是左）给maxparent的左
				{
					maxparent->_left = leftmax->_left;
					delete leftmax;
				}
				else
				{
					maxparent->_right = leftmax->_left;
					delete leftmax;
				}
			}
			return true;
		}

SearchR（查找）

其实在介绍完删除操作之后，查找操作就很简单了：

壳接口SearchR中调用递归函数_SearchR：

	Node* SearchR(const K& key)
	{
		return _SearchR(_root, key);
	}

函数_SearchR的参数为根结点的指针与要查找的数据（这里不需要指针的引用传参了，是因为我们不需要建立与上层的链接了）：

在查找过程中：

• 若目标结点小于当前结点，在左子树中递归寻找；
• 若目标结点大于当前结点，在右子树中递归寻找；
• 若等于则返回这个目标结点的指针。

如果root == nullptr 说明找到底也没有目标结点，返回nullptr即可：

	Node* _SearchR(Node* root, const K& key)
	{
		if (root == nullptr)
			return nullptr;

		if (key < root->_key)
		{
			return _SearchR(root->_left, key);
		}
		else if(key > root->_key)
		{
			return _SearchR(root->_right, key);
		}
		else
		{
			return root;
		}
	}

这里提一下为什么在之前的插入与删除操作中没有复用这个查找函数，因为插入与删除的操作在查找到目标结点后，都需要修改与上一层调用中结点的链接，所以这里的查找函数还是不要凑热闹。

源码概览

namespace qqq
{
	//递归
	template<class K>
	struct BSTreeNodeR
	{
		BSTreeNodeR<K>* _left;
		BSTreeNodeR<K>* _right;
		K _key;

		BSTreeNodeR(const K& key)
			: _key(key)
			, _left(nullptr)
			, _right(nullptr)
		{}
	};

	template<class K>
	class BSTreeR
	{
	public:
		typedef BSTreeNodeR<K> Node;
	public:
		BSTreeR()
			: _root(nullptr)
		{}
		BSTreeR(const BSTreeR<K>& ctree)
		{
			_constructor(_root, ctree._root);
		}
		BSTreeR<K>& operator=(BSTreeR<K> ctree)
		{
			swap(_root, ctree._root);
			return *this;
		}
		~BSTreeR()
		{
			_destructor(_root);
		}

		bool InsertR(const K& key)
		{
			return _InsertR(_root, key);
		}

		bool EraseR(const K& key)
		{
			return _EraseR(_root, key);
		}

		Node* SearchR(const K& key)
		{
			return _SearchR(_root, key);
		}

		void InOrderR()  //测试代码
		{
			_InOrderR(_root);
			cout << endl;
		}
	protected:
		void _constructor(Node*& root, Node* croot)
		{
			if (croot == nullptr)
				return;

			Node* newnode = new Node(croot->_key);
			root = newnode;
			_constructor(root->_left, croot->_left);
			_constructor(root->_right, croot->_right);
		}

		void _destructor(Node*& root)
		{
			if (root == nullptr)
				return;

			_destructor(root->_left);
			_destructor(root->_right);
			delete root;
			root = nullptr;
		}

		bool _InsertR(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				Node* newnode = new Node(key);
				root = newnode;
				return true;
			}

			if (key < root->_key)
			{
				return _InsertR(root->_left, key);
			}
			else if (key > root->_key)
			{
				return _InsertR(root->_right, key);
			}
			else
			{
				cout << "The key has existed" << endl;
				return false;
			}
		}
		bool _EraseR(Node*& root, const K& key)
		{
			//递归找到要删的结点
			if (root == nullptr)
			{
				cout << "The key does not exist" << endl;
				return false;
			}
				
			if (key < root->_key)
			{
				return _EraseR(root->_left, key);
			}
			else if (key > root->_key)
			{
				return _EraseR(root->_right, key);
			}
			else //找到
			{
				if (root->_left == nullptr) //左为空
				{
					Node* deltemp = root;
					root = root->_right;
					delete deltemp;

					return true;
				}
				else if (root->_right == nullptr) //右为空
				{
					Node* deltemp = root;
					root = root->_left;
					delete deltemp;

					return true;
				}
				else//有两个个孩子时，找左树中的最大元素，交换后再调该函数
				{
					Node*& leftMax = root->_left;
					while (leftMax->_right)
					{
						leftMax = leftMax->_right;
					}
					std::swap(leftMax->_key, root->_key);//交换值

					return _EraseR(leftMax, key);
				}
			}
		}
		Node* _SearchR(Node* root, const K& key)
		{
			if (root == nullptr)
				return nullptr;

			if (key < root->_key)
			{
				return _SearchR(root->_left, key);
			}
			else if(key > root->_key)
			{
				return _SearchR(root->_right, key);
			}
			else
			{
				return root;
			}
		}
		void _InOrderR(Node* root) //测试代码
		{
			if (root == nullptr)
				return;

			_InOrderR(root->_left);
			cout << root->_key << " ";
			_InOrderR(root->_right);
		}
		
        //树根节点指针
		Node* _root;
	};

}

总结

到此，关于二叉搜索树的介绍与实现就结束了
在本文刚开始的时候，我们也提到了一些二叉搜索树的弊端，它最坏的时间复杂度为O(N)。在接下来的文章中将会介绍一些平衡二叉树。相比于二叉搜索树又增加了一些特征，以解决这种漏洞

如果大家认为我对某一部分没有介绍清楚或者某一部分出了问题，欢迎大家在评论区提出

如果本文对你有帮助，希望一键三连哦

希望与大家共同进步哦