树状数组(Binary Indexed Tree)

树状数组(Binary Indexed Tree)

思路介绍

树状数组可以高效的维护和查询前缀和或者区间和

如果数组是静态的，那么很好处理，我们只需要预处理前缀和即可，复杂度是O(n)

但如果这个数组是动态的，那么将会变得发杂起来

我们不可能对每一次变化都进行前缀和操作，这样时间复杂度过高，所以我们采用更高级的方法实现

假设我们有如下的数组：

有这样一个朴素的想法，主要思路是二分的想法：

即， 每两个数求一次和，那么求和的过程将会被缩减一半：

接着这个思路继续，我们还可以继续对两两值求和，只到只剩下一个数为止。

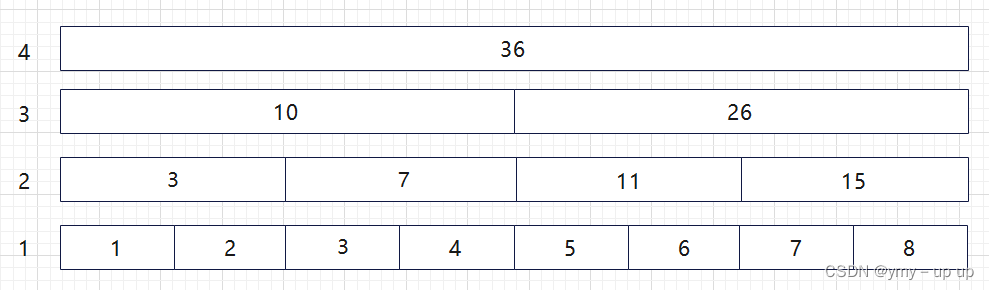
这样我们就可以操作很少的数得到一段区间的和

举个例子：如果我想知道1-5之间的和，我只需要读取第3行的10然后加上第一行的5得15

这样时间将大大减小，如果要修改某个值，也只需要更改包含该区间的和即可

优化

注意一点，在以上，我们有些数是永远用不到的，如下图：

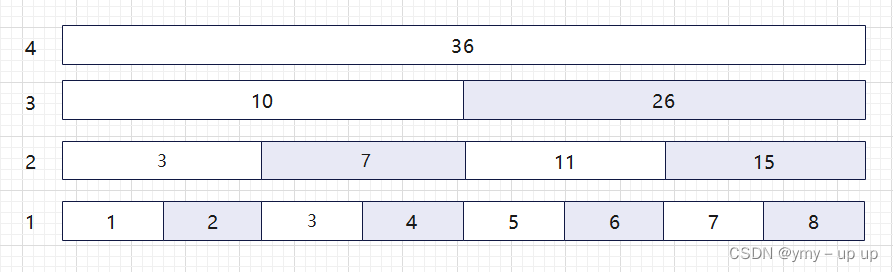
如果我们要求1-5的和，需要第三行的10以及第一行的5，求1-6的和，只需要第三行10，第二行11，

观察可知，每一行的偶数个都是不需要的。

删去后发现实际上剩下的数与原本的数一致

维护与查询思路

我们知道了基本原理，那我们该如何获取我需要的区间和呢，具体的数组下标是什么

直接给出结论：

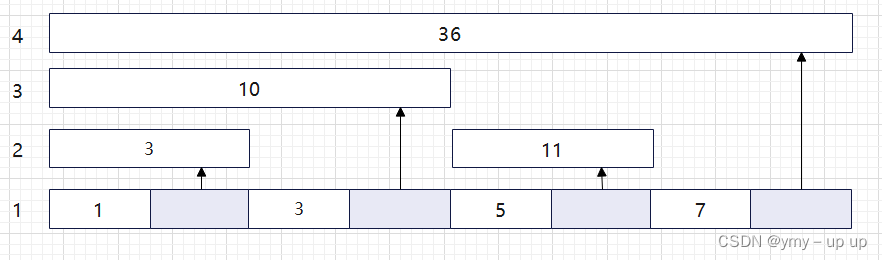
假设我们要查询区间1-7的和， 即sum(7);

我们对输入的数的二进制进行操作，每次去掉二进制下最后一个1

具体的看：

7的二进制是 111， 去掉最后的1 变成 110 ，即 6

之后再去掉变成 100， 即4

再去掉后就没了，所以1-7的区间和为： sum(7) = tree[7] + tree[6] + tree[4]; (tree数组即为上面将无用数据删除后形成的数组)

现在我们更改 a₃

我们需要修改的下标同样也是对二进制进行操作，每次在最后的1上加1.

3的二进制为011， 加一为 100 即 4

再加 1000 即 8 ,以此类推直到达到边界

编码实现

在维护和查询思路中，其核心便是求二进制下最后一个1所代表的数

我们通过lowbit()函数获得这个数的最后一位1所代表的数。

int lowbit(int x){
    return x & (-x);
}

二进制复习

代码及其精简，涉及二进制相关，下面是于此相关的二进制小总结（如果会二进制默认跳过）

这两篇博客写的很好可以看看：

位运算全面总结，关于位运算看这篇就够了_unique_pursuit的博客-CSDN博客_位运算

负数的二进制表示_storm_fury的博客-CSDN博客_负数二进制

二进制基本符号

符号	描述	运算规则	实例
&	与	两个位均为1的时候，结果才为1	1001&0101 = 0001， 0000 & 0001 = 0000
|	或	两个位都为0的时候，结果才为0	0111|0000 = 0111, 0000 | 0000 = 0000
^	异或	两个位相同为0，个位不同为1	0101^0000 = 0101 , 0001^0001 = 0000
~	取反	按位取反，0变1，1变0	~0001 = 1110， ~0000 = 1111
<<	左移	各二进制位左移若干位，高位丢弃，低位补0	0001<<k=0100，k=2，k kk是左移的位数，这里k = 2 k=2k=2
>>	右移	各二进位全部右移若干位，对无符号数，高位补0，有符号数，右移补1	0100>>k=0001，k=2，k kk是右移的位数，这里k = 2 k=2k=2

位运算常用玩法

特别要点出来的是相乘和相除的操作：

a<<1 == a∗2

a > > 1 == a / 2

这两在二分算法中有着重要运用，相对于普通相除来说应对数据溢出有奇效

a << 2 == a * 4

a << 1 | 1 == a * 2 + 1

这两在线段树中有用武之地

负数的二进制存储：

在计算机中，
正数是直接用原码表示的，如单字节5，在计算机中就表示为：0000 0101。
负数以其正值的补码形式表示，如单字节-5，在计算机中表示为：1111 1011。

负数的补码是由其正数的二进制原码转化而成

5 的原码为0000 0101， -5 的原码为 1000 0101，最前面的1是符号位，

储存的时候将符号位不变其他按位取反得： 1111 1010 ，最后加一得： 1111 1011；

lowbit的二进制解释

x & (-x)

我们可以知道负数在计算机中以补码的形式存储。

我们根据负数的存储条件，先去掉负数存储的最后一步，即加一操作

0100 1100 —> 1011 0011, 此时我们进行&操作，得到的数是0，但应为最后加了一个一，这个一会不断前进到原码第一个一的位置

具体的情况那笔演示一下可以得出，所以最后&的结果便是可以得到最低为1代表的数

lowbit巧妙的运用了负数补码的性质。

代码解释

基础准备

#include<bits/stdc++.h>
using namespace std;
const int length = 20; // tree数组长度，要用const修饰
int arr[10] = {0,1,2,3,4,5,6,7,8,9};
int tree[length];

lowbit函数

int lowbit(int x){
    return x & (-x);
}

查询前缀和操作

int sum(int number){
    int ans = 0;
    while(number > 0){
        ans += tree[number];
        number -= lowbit(number);
    }
    return ans;
}

更新数值操作

void update(int index, int d){ //修改元素， arr[index] = arr[index] + d;
    while(index <= length){
        tree[index] += d;
        index += lowbit(index);
    }
}

测试一下

signed main()
{
    //可以这样理解，一开始tree数组储存的是length个0的前缀和，之后我们对这些0进行加减操作
    for(int temp = 0 ; temp < 10 ; temp++)
        update(temp+1,arr[temp]);
    cout << "old:" << sum(5) << "\n";
    update(2,4);
    cout << "new:" << sum(5);
    return 0;
}
/*
old:10
new:14
*/

树状数组基本应用

区间修改+单点查询

对于一个数组A={a₁, a₂, a₃ …}, 如果我们要对一段区间进行修改，最简单的方法是对这一整个区间的每一个数进行修改

但是这样的时间复杂度过高，会TLE，所以我们可以采用树状数组+差分数组的方式来提高效率

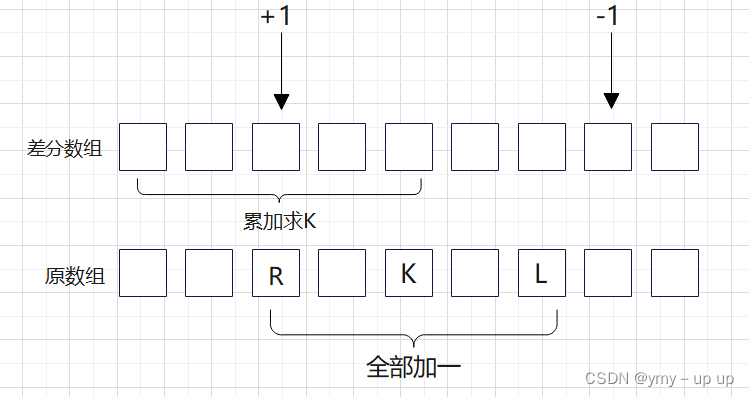
一直如果想对一段区间整体加减，我们只需要对差分数组的两个点进行修改，这样就实现了将时间复杂度由O（N）转化为O（1）

同时如果想查询一个数的值，我们需要对差分数组进行求和，而求和这件事对于树状数组不是难事

所以我们可以将差分数组用树状数组来表示，这样就可以实现区间修改+单点查询

我们举个例子：hdu 1556

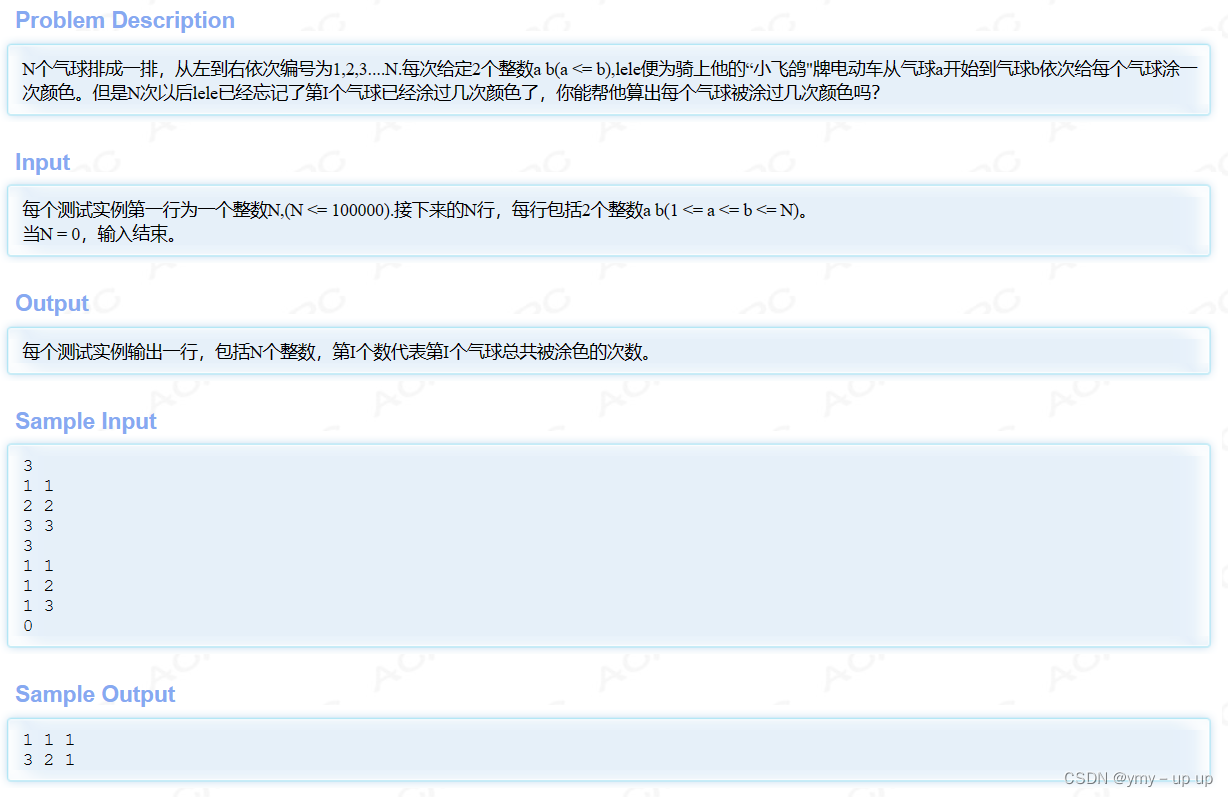
代码

#include<bits/stdc++.h>
using namespace std;
const int N = 200000;
int tree[N];
int total;
#define lowbit(x) ((x) & -(x))
void update(int index, int d){
    while(index <= N){
        tree[index] += d;
        index += lowbit(index);
    }
}
int sum(int index){
    int ans = 0;
    while(index > 0){
        ans += tree[index];
        index -= lowbit(index);
    }
    return ans;
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    while(cin >> total){
        memset(tree, 0, sizeof(int)*N); //因为初始的时候每个气球的次数都是0，所以差分数组也全是0
        for(int temp = 0 ; temp < total ; temp++){
            int left, right;
            cin >> left >> right;
            update(left, 1); //起始端点加一
            update(right + 1, -1); // 结尾端点的后一个减一，与差分数组操作完全一致
        }
        for(int temp = 1 ; temp <= total ; temp++)
            cout << sum(temp) << " ";
        cout << "\n";
    }
    return 0;
}

区间修改+区间查询

我们先定义两个数组， 一个是原数组A， 一个是差分数组 D

如果我们要想对区间进行修改，那么最好的办法便是通过差分数组，所以我们如过可以得到差分数组与原数组和的关系，我们就可以通过差分数组快速且高效的完成区间修改和区间查询。

推导过程如下, D为差分数组的值
$$\begin{array}{rl}& a_1+a_2+a_3+a_4+.....+a_k\\ & \\ & \{\begin{array}{ll}& D_1+(D_1+D_2)+(D_1+D_2+D_3)+....+(D_1+D_2+...+D_k)\\ & \\ & k{D}_1+(k-1)D_1+(k-2)D_2+....+(k-(k-1))D_k\\ & \\ & k(D_1+D_2+D_3+...+D_k)-(D_2+2D_3+...+(k-1)D_k)\end{array}\\ & \\ & \because a_1+a_2+a_3+a_4+.....+a_k=k\sum _{i=1}^k{D}_i-\sum _{i=1}^k(i-1)D_i\end{array}$$
所以我们可以用两个树状数组分别来实现两个的求和

一个来实现D_i， 一个来实现 （i-1）D_i

举个例子：洛谷P3372

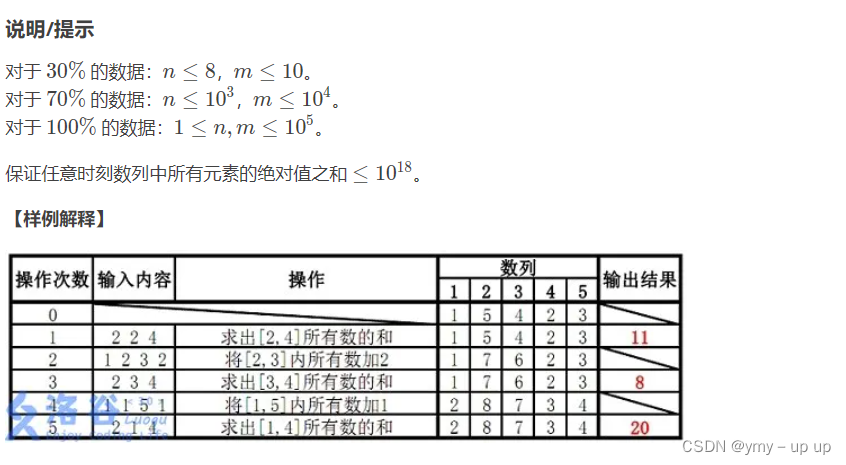
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) ((x) & -(x))
typedef long long int lli;
const lli total = 100010; 
lli tree1[total], tree2[total];  //D, (i-1)D
lli total_num, total_oper;
void update1(int i, int d){while(i <= total){tree1[i] += d; i += lowbit(i);}} //分别处理两颗树
void update2(int i, int d){while(i <= total){tree2[i] += d; i += lowbit(i);}}
lli sum1(int i){lli ans = 0; while(i > 0){ans += tree1[i];i -= lowbit(i);}return ans;}
lli sum2(int i){lli ans = 0; while(i > 0){ans += tree2[i]; i -= lowbit(i);}return ans;}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> total_num >> total_oper;
    lli old = 0, a;
    for(int temp = 1 ; temp <= total_num ; temp++){ //求差分，以及（i-1）D
        cin >> a;
        update1(temp, a-old);
        update2(temp, (temp - 1)*(a - old));
        old = a;
    }
    int order, num1, num2, div_;
    for(lli temp = 0 ; temp < total_oper ; temp++){
        cin >> order >> num1 >> num2;
        if(order == 1){
            cin >> div_;
            update1(num1, div_);
            update1(num2 + 1, -div_);
            update2(num1, (num1 - 1)*div_); //注意要乘上（i-1）
            update2(num2 + 1, num2*-div_);
        }else{
            lli tot1 = (num1 - 1)*sum1(num1 - 1) - sum2(num1 - 1);
            lli tot2 = num2*sum1(num2) - sum2(num2);
            cout << tot2 - tot1 << "\n";
        }
    }
    return 0;
}

二维区间修改 + 二维区间查询

我们通过之前的前缀和与差分知识可以知道：

差分是前缀和的逆运算，

即二维差分数组的定义是：D为差分数组， a为原数组
$$D[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$$

代表的即是图中阴影部分。

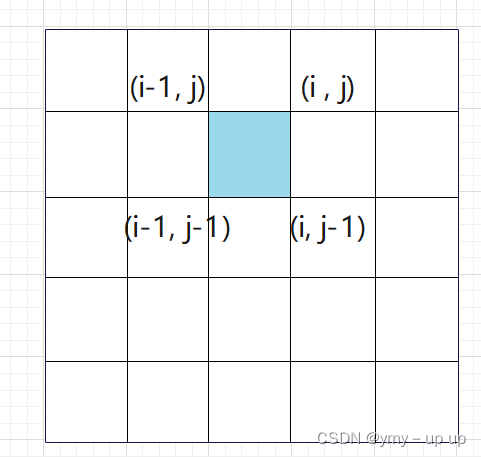
同过二维差分数组，我们也可以得到原数据
$$a[c][d]=\sum _{i=1}^c\sum _{j=1}^{d}d[i][j]$$
因为是二维求和，所以我们的树状数组也要变成二维的树状数组

同时update，sum函数都要改变

每次i行变化lowbit(i), j行变化lowbit(j)

如下：

update(二维)

void update(int x, int y, int d){
    for(int temp = y ; temp <= N ; temp += lowbit(temp)){
        for(int temp2 = x ; temp2 <= N ; temp2 += lowbit(temp2))
            arr[temp][temp2] += d;
    }
}

sum(二维)

int sum(int x, int y){
    int ans = 0;
    for(int temp = y ; temp > 0 ; temp -= lowbit(temp)){
        for(int temp2 = x ; temp2 > 0 ; temp2 -= lowbit(temp2))
            ans += arr[temp][temp2];
    }
    return ans;
}

我们测试一下：(测试只是为了看的更清楚，属于题外话，可以跳过)

基本信息

#include<bits/stdc++.h>
#define lowbit(x) (x & -(x))
using namespace std;
const int N = 10;
int arr[N][N], test[N][N];//二维树状数组， 原数组

辅助函数

void Init(){//初始化原数组
    int begin = 1;
    for(int temp = 1 ; temp < N ; temp++){
        for(int temp2 = 1 ; temp2 < N ; temp2++)
            test[temp2][temp] = begin++;
    }
}
void Change(int a, int b, int i, int j, int d){ //区间修改，修改(a,b)到(i,j)元素
    update(a,b,d); update(i+1,j+1,d);
    update(a,j+1,-d); update(i+1,b,-d);
}
void Print1(){//打印由树状数组获得的原数组数据
    for(int temp = 1 ; temp < N ; temp++){
        for(int temp2 = 1 ; temp2 < N ; temp2++)
            cout << sum(temp, temp2) << " ";
        cout << "\n";
    }
    cout << "-----------------------\n";
}
void Print2(){//打印原数组， 用于对照
    for(int temp = 1 ; temp < N ; temp++){
        for(int temp2 = 1 ; temp2 < N ; temp2++)
            cout << test[temp][temp2] << " ";
        cout << "\n";
    }
    cout << "-------------------------\n";
}

开始

signed main()
{
    Init();
    Print2();
    for(int temp = 1 ; temp < N ; temp++){
        for(int temp2 = 1 ; temp2 < N ; temp2++){
            int add = test[temp][temp2] - test[temp - 1][temp2] - test[temp][temp2 - 1] + test[temp-1][temp2-1];
            update(temp,temp2,add);
        }
    }
    Print1();
    Change(3,3,5,5,50);
    Print1();
}
/*
1 10 19 28 37 46 55 64 73
2 11 20 29 38 47 56 65 74
3 12 21 30 39 48 57 66 75
4 13 22 31 40 49 58 67 76
5 14 23 32 41 50 59 68 77
6 15 24 33 42 51 60 69 78
7 16 25 34 43 52 61 70 79
8 17 26 35 44 53 62 71 80
9 18 27 36 45 54 63 72 81
-------------------------
1 10 19 28 37 46 55 64 73
2 11 20 29 38 47 56 65 74
3 12 21 30 39 48 57 66 75
4 13 22 31 40 49 58 67 76
5 14 23 32 41 50 59 68 77
6 15 24 33 42 51 60 69 78
7 16 25 34 43 52 61 70 79
8 17 26 35 44 53 62 71 80
9 18 27 36 45 54 63 72 81
-----------------------
1 10 19 28 37 46 55 64 73
2 11 20 29 38 47 56 65 74
3 12 71 80 89 48 57 66 75
4 13 72 81 90 49 58 67 76
5 14 73 82 91 50 59 68 77
6 15 24 33 42 51 60 69 78
7 16 25 34 43 52 61 70 79
8 17 26 35 44 53 62 71 80
9 18 27 36 45 54 63 72 81
-----------------------
*/

二维区间查询
$$\begin{array}{rl}& 假设我们要查询原数组a[][]在区间(a,b)到(c,d)的和，则:\\ & \sum _{i=a}^c\sum _{j=b}^{d}a[i][j]=\sum _{i=1}^c\sum _{j=1}^{d}a[i][j]-\sum _{i=1}^c\sum _{j=1}^{b-1}a[i][j]-\sum _{i=1}^{a-1}\sum _{j=1}^{d}a[i][j]+\sum _{i=1}^{a-1}\sum _{j=1}^{b-1}a[i][j]\\ & 所以问题就转化为求\sum _{i=1}^n\sum _{j=1}^{m}a[i][j]\\ & \\ & 又\because a[i][j]=\sum _{k=1}^i\sum _{l=1}^{j}D[k][l]\\ & \therefore \sum _{i=1}^n\sum _{j=1}^{m}a[i][j]=\sum _{i=1}^n\sum _{j=1}^m\sum _{k=1}^i\sum _{l=1}^{j}D[k][l]\\ & \\ & 统计一下每个D[k][l]出现过多少次\\ & D[1][1]出现了x\ast y次，D[1][2]出现了x\ast (y-1)次\\ & \\ & \therefore D[k][l]出现了(n-k+1)\ast (m-l+1)次\\ & \therefore \sum _{i=1}^n\sum _{j=1}^m\sum _{k=1}^i\sum _{l=1}^{j}D[k][l]=\sum _{i=1}^n\sum _{j=1}^{m}D[i][j]\ast (n-i+1)\ast (m-j+1)\\ & 将式子乘开可以得知:\\ & \\ & \sum _{i=a}^c\sum _{j=b}^{d}a[i][j]=((n+1)(m+1)\sum _{j=1}^{m}D[i][j])-((m+1)\sum _{j=1}^{m}D[i][j]\ast i)-\\ & ((n+1)\sum _{j=1}^{m}D[i][j]\ast j)+(\sum _{j=1}^{m}D[i][j]\ast i\ast j)\end{array}$$
所以我们需要四个树状数组来实现这个效果

举个例子（洛谷P4514）//本题使用CDQ分治会更好

二维数组解决此类问题的缺点是内存占用大

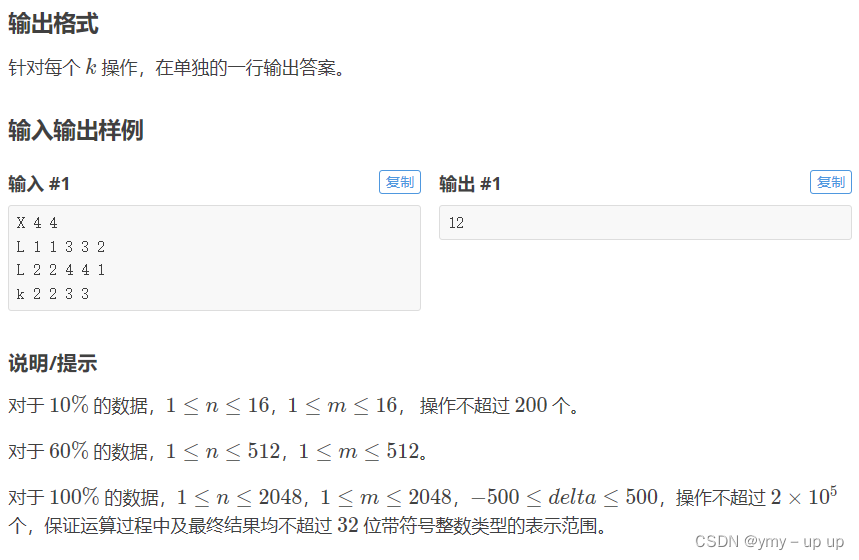
具体的思路都在上面了，直接给代码咯

小小唠一下，这是本菜鸡的第一道紫题…

开心

#include<bits/stdc++.h>
#define lowbit(x) (x & -(x))
using namespace std;
const int N = 2050;
int t1[N][N], t2[N][N], t3[N][N], t4[N][N];
int n,m;
void update(int x, int y, int d){
    for(int temp = x ; temp <= m ; temp += lowbit(temp)){
        for(int temp2 = y ; temp2 <= n ; temp2 += lowbit(temp2)){
            t1[temp][temp2] += d; t2[temp][temp2] += (d*x);
            t3[temp][temp2] += (d*y) ; t4[temp][temp2] += (d*x*y);
        }
    }
}
int sum(int x, int y){
    int ans = 0;
    for(int temp = x ; temp > 0 ; temp -= lowbit(temp)){
        for(int temp2 = y ; temp2 > 0 ; temp2 -= lowbit(temp2)){
            int a = (x+1)*(y+1)*t1[temp][temp2];
            int b = (y+1)*t2[temp][temp2];
            int c = (x+1)*t3[temp][temp2];
            ans += a-b-c+t4[temp][temp2];
        }
    }
    return ans;
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    string order;
    cin >> order >> n >> m;
    while(cin >> order){
        if(order == "L"){
            int a,b,c,d,add;
            cin >> a >> b >> c >> d >> add;
            update(a,b,add); update(c+1,d+1,add);
            update(a,d+1,-add); update(c+1,b,-add);
        }else{
            int a,b,c,d;
            cin >> a >> b >> c >> d;
            cout << sum(c,d)+sum(a-1,b-1)-sum(c,b-1)-sum(a-1,d);
            cout << "\n";
        }
    }
    return 0;
}