线段树 (Segment Tree)

线段树 (Segment Tree)

概念引入

线段树和树状数组一样，是一个对区间进行操作的工具

之所以叫工具，因为线段树更像一个工具，而不是一个具体的算法

它比树状数组更加有用且有适配性，可以说大部分能用树状数组解决的问题都可以用线段树解决

线段树可以将O(N)转变为O(logN)

简单来说，线段树就是一颗二叉树，或者说是一个满二叉树

思路和树状数组差不多，也是分治的思想，将一段区间不断二分，通过二分的结果来合并成总结果

假设我们有一个有五个元素的数组，那么可以认为区间范围是[1,5]

那么就可以弄出这样一个线段树

每一个区间都可以看成是一个二叉树的结点，这个结点所储存的信息就是该区间的信息

这些信息可以是区间和，最大值，最小值等等

举个例子：

要求[3,5]的和，我们可以吧[3,3]的和与[4,5]的和加在一起，这样效率就会变得很高

代码+基本操作

建树

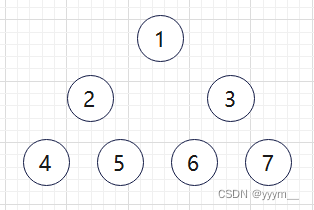
由图可以知道，或者说这是二叉树的特性：

某一结点的编号为 $i$ , 那么它的左儿子的编号是 $2\ast i$ ,她的右儿子的编号是 $2\ast i+1$

接下来我们就可以利用该特性来建树，值得一提的是，所开的空间长度是4倍数据的长度，具体为啥自行百度，不是重点

我们采用递归建树：

//基础头文件及准备工作
#include<bits/stdc++.h>
using namespace std;
const int N = 100;
int length; //数据长度
int arr[N]; //原数据
struct Tree{
    int sum; //我们这里结点信息是区间和
    int left, right; //区间的开始而结尾，并不是左孩子和右孩子
}seg[4*N]; //这个就是我们的线段树

真正的建树函数

void build_tree(int l, int r, int i){ //参数的意思为：区间左端点，右端点，二叉树的结点编号
    //首先让该节点的左右分别对应上，因为left，right确定该节点到底对应哪个区间
    seg[i].left = l; seg[i].right = r;
    if(l == r){ //如果区间左右一样，即[1,1],[3,3]这种，就说明已经到底部了
        seg[i].sum = arr[l]; //这种区间的区间和自然等于原数据
        return;
    }
    int mid = (l + r) >> 1; //排除了区间左右相等的情况，那我们就将区间对半分
    build_tree(l,mid,i*2); //建立左孩子， i*2代表左孩子编号
    build_tree(mid + 1, r, i*2 + 1); //建立右孩子
    //区间和自然是左右孩子区间和之和，即[1,3]之和是[1,2]之和与[3,3]之和相加
    seg[i].sum = seg[i*2].sum + seg[i*2 + 1].sum;
}

单点修改 + 区间查询

我们先讲区间查询

区间查询

如图，假如我们想要求得[1,5]的和，我们可以通过[1,3]以及[4,5]的和来求得

由线段树的特性我们可以递归搜索只到找到该区间

Search()

int Search(int l, int r, int i){ //参数所代表的意义为： 要搜索区间的左端点，右端点， 当前结点的编号 
    //如果搜索区间的左右端点与当前结点代表的左右区间的端点一致，说明找到了该区间
    if(seg[i].right == r && seg[i].left == l)
        return seg[i].sum; //返回该区间的区间和
    //如果要搜索的区间完全被左子树包含，那么只需要搜索左子树
    if(seg[i << 1].right >= r) return Search(l,r, i << 1);
    //如果要搜索的区间完全被右子树包含，那么只需要搜索右子树
    else if(seg[i << 1 | 1].left <= l) return Search(l,r,i << 1 | 1);
    //如果要搜索的区间夹在中间，那么搜索左右子树，然后相加
    else{
        lli num1 = Search(l, seg[i << 1].right, i << 1);
        lli num2 = Search(seg[i << 1 | 1].left, r, i << 1 | 1);
        return num1 + num2;
    }
}

• 解释

  如何理解一下语句

  if(seg[i << 1].right >= r) return Search(l,r, i << 1);
  else if(seg[i << 1 | 1].left <= l) return Search(l,r,i << 1 | 1);
  else{
      lli num1 = Search(l, seg[i << 1].right, i << 1);
      lli num2 = Search(seg[i << 1 | 1].left, r, i << 1 | 1);
      return num1 + num2;
  }
  

  我们把搜索经过的区间标粗

  

  之后我们把搜索区间与结点代表区间的三种关系给出：

  

  首先我们要明确 $l$ , $r$ 的意思是在区间 [$seg[i].left$ , $seg[i].right$ ] 搜索区间[ $l$ , $r$]

  所以区间 [$l$ ,$r$] 必须包含在区间内，

  所以在情况1 ,2中，$l$，$r$的值并未发生改变，

  而情况3，为了满足上述条件，所以$l$，$r$ 变为{[ $l$, $seg[i<<1].right$ ]} ,{[ $seg[i<<1|1].left$ , $r$ ]}

单点修改

既然是单点修改，我们也就必须要找到具体的那个点

即假如我要修改第四个点，我就需要找到区间[4,4]

具体的路径如下图

注意：

结点中存放的数据是区间和，所以要同步修改路径上的区间和

Change_point()

void Change_point(int target, int d, int i){ //要修改的数的下标，要加上的数， 结点编号
    if(seg[i].left == seg[i].right){ //如果该节点的左右端点一样，即出现[4,4]这种情况
       seg[i].sum += d; //修改区间和
       return;
    }
    if(seg[i*2].right >= target) //与搜寻区间和一致，只不过这次是判断点与区间的关系
        Change_point(target,d,i*2);
    else
        Change_point(target, d, i*2 + 1);
    seg[i].sum = seg[i*2].sum + seg[i*2 + 1].sum; //某一结点的区间和等于其左右结点的区间和
    return;
}

给出一道模板题， 可以试一下

P3374 【模板】树状数组 1

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli N = 1000000;
lli total_num, total_order;
lli arr[N];
struct Tree{
    int sum;
    int left, right;
}seg[4*N];
void Build(lli l, lli r, lli i){
    seg[i].left = l; seg[i].right = r;
    if(l == r){
        seg[i].sum = arr[l];
        return ;
    }
    lli mid = (l + r) >> 1;
    Build(l, mid, i << 1);
    Build(mid + 1, r, i << 1 | 1);
    seg[i].sum = seg[i << 1].sum + seg[i << 1 | 1].sum;
    return ;
}
int Search(lli l, lli r, lli i){
    if(seg[i].right == r && seg[i].left == l)
        return seg[i].sum;
    if(seg[i << 1].right >= r) return Search(l,r, i << 1);
    else if(seg[i << 1 | 1].left <= l) return Search(l,r,i << 1 | 1);
    else{
        lli num1 = Search(l, seg[i << 1].right, i << 1);
        lli num2 = Search(seg[i << 1 | 1].left, r, i << 1 | 1);
        return num1 + num2;
    }
}
void Change_point(lli target, lli d, lli i){
    if(seg[i].left == seg[i].right){
        seg[i].sum += d;
        return ;
    }
    if(seg[i << 1].right >= target) Change_point(target, d, i << 1);
    if(seg[i << 1 | 1].left <= target) Change_point(target, d, i << 1 | 1);
    seg[i].sum = seg[i << 1].sum + seg[i << 1 | 1].sum;
}

signed main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    cin >> total_num >> total_order;
    for(int temp = 1; temp <= total_num ; temp++)
        cin >> arr[temp];
    Build(1, total_num, 1);
    for(int temp = 0 ; temp < total_order ; temp++){
        lli order, one, two;
        cin >> order >> one >> two;
        if(order == 1)
            Change_point(one, two ,1);
        else
            cout << Search(one, two, 1) << "\n";
    }
    return 0;
}

区间修改 + 区间查询

Lazy_Tag (无 push_down 版)

注：无 push_down版本只是一个中间产物，最终还是要加上push_down,但是了解无push_down可以加深理解

区间修改

首先要明确一点：

假设我们要对[1，4]内所有的数加一， 我们不可能通过上述的单点修改来实现，毕竟这样的复杂度过高

这个时候我们就需要引入一个“懒人标记” —— Lazy-tag

这个标记的意思是代表这个区间内每一个值都要加减

先来说说这个思路的核心思想。

假设我们要想求得[1,3]的区间和

我们要获得[1,3]的sum，以及搜寻过程中的Lazy总值

然后sum + Lazy总值*区间内数的个数

拿[1,3]举例，sum代表着不考虑[1,3]以及其之上Lazy标签的影响时，[1,3]的区间和

假设[1,3]原本和为10， 现在让[1,3]每个数+1，[1,3]的Lazy是1，sum却依然等于10

举个例子

十个元素分别是 1，2，3，4，5，6，7，8，9，10

初始时：[1,5]的Lazy值为0， sum为15 ， [1,3]的Lazy值为0，sum为6

我们先让[1,3]区间内每个数加上1

那么此时[1,5]的Lazy值为0， sum却变成了18，[1,3]的Lazy值为0，sum为6

因为[1,5]包含[1,3] ， 而[1,5]的sum是不考虑之后的lazy标签影响的，也就是[1,3]内区间的影响

但[1,3]区间确确实实是每个数加了一个1，为了让结果保持一致，我们也只能在[1,5]的sum上加上等价的数

接下来就是代码了：

前期准备

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli N = 100010;
lli arr[N];
struct Tree{ //线段树
    lli sum, Lazy; //和以及Lazy标签
    lli left, right; //结点代表的区间左端点值，右端点值
}seg[4*N];

建树

void Build(lli l, lli r, lli i){ //代表的意义为：要搜索区间的左端点，右端点，结点编号
   	//初始时的操作与普通情况一致，只需要将Lazy赋值为0
    seg[i].left = l, seg[i].right = r, seg[i].Lazy = 0;
    if(l == r){
        seg[i].sum = arr[l];
        return ;
    }
    lli mid = (l + r) >> 1;
    Build(l, mid, i << 1);
    Build(mid + 1, r, i << 1 | 1);
    seg[i].sum = seg[i << 1].sum + seg[i << 1 | 1].sum;
}

区间修改

void modify(lli l, lli r, lli d, lli i){ //意义为：要修改区间的左端点，右端点，增加的数，结点编号
    if(seg[i].left == l && seg[i].right == r){ //当节点代表的区间与要修改区间一致，说明找到了
        seg[i].Lazy += d; //Lazy += 要修改的值 ， 注意是 += ，因为 Lazy可以叠加
        return;
    }
    seg[i].sum += (r - l + 1)*d; //为了sum达到正确的值，在原区间上应该加上一定的值
    //之后与普通搜索类似，分三种情况讨论
    if(seg[i << 1].right >= r) modify(l,r,d, i << 1);
    else if(seg[i << 1|1].left <= l) modify(l,r,d, i << 1|1);
    else{
        modify(l,seg[i << 1].right, d, i << 1);
        modify(seg[i << 1 | 1].left, r, d, i << 1|1);
    }
}

• 解释

  seg[i].sum += (r - l + 1)*d; //如何去理解
  

  

  首先要寻找的区间一定包含在当前区间内

  假设当前区间和为10，要寻找区间每个数+1，

  那么当要寻找区间每个数+1后，当前区间可以理解为右5个数+1

  也就是说：当前区间的和要加上(寻找区间内包含的数*增加的量)

  而（r-l+1）就是搜寻区间内包含数的个数

区间查询

lli query(lli l, lli r, lli i, lli tag){ //意义为：要搜索区间的左端点，右端点，结点编号，搜寻过程中的Lazy总值
    tag += seg[i].Lazy;// 首先总值要包括当前结点的Lazy值
    if(seg[i].left == l && seg[i].right == r){ //如果找到要搜寻的区间
        return seg[i].sum + (seg[i].right - seg[i].left + 1)*tag; //返回确切的区间和，即加上了Lazy
    }
    //之后按照三种情况分开寻找
    if(seg[i << 1].right >= r) return query(l, r, i << 1, tag);
    else if(seg[i << 1 | 1].left <= l) return query(l,r, i << 1 | 1, tag);
    else{
        lli num1 = query(l, seg[i << 1].right, i << 1, tag);
        lli num2 = query(seg[i << 1 | 1].left, r, i<< 1 | 1, tag);
        return num1 + num2;
    }
}

下面有一道模板题，用上述知识可以完成

P3372 【模板】线段树 1

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli N = 100010;
lli total_num, total_oper;
lli arr[N];
struct Tree{
    lli sum, Lazy;
    lli left, right;
}seg[4*N];
void Build(lli l, lli r, lli i){
    seg[i].left = l, seg[i].right = r, seg[i].Lazy = 0;
    if(l == r){
        seg[i].sum = arr[l];
        return ;
    }
    lli mid = (l + r) >> 1;
    Build(l, mid, i << 1);
    Build(mid + 1, r, i << 1 | 1);
    seg[i].sum = seg[i << 1].sum + seg[i << 1 | 1].sum;
}
void modify(lli l, lli r, lli d, lli i){
    if(seg[i].left == l && seg[i].right == r){
        seg[i].Lazy += d;
        return;
    }
    seg[i].sum += (r - l + 1)*d;
    if(seg[i << 1].right >= r) modify(l,r,d, i << 1);
    else if(seg[i << 1|1].left <= l) modify(l,r,d, i << 1|1);
    else{
        modify(l,seg[i << 1].right, d, i << 1);
        modify(seg[i << 1 | 1].left, r, d, i << 1|1);
    }
}
lli query(lli l, lli r, lli i, lli tag){
    tag += seg[i].Lazy;
    if(seg[i].left == l && seg[i].right == r){
        return seg[i].sum + (seg[i].right - seg[i].left + 1)*tag;
    }
    if(seg[i << 1].right >= r) return query(l, r, i << 1, tag);
    else if(seg[i << 1 | 1].left <= l) return query(l,r, i << 1 | 1, tag);
    else{
        lli num1 = query(l, seg[i << 1].right, i << 1, tag);
        lli num2 = query(seg[i << 1 | 1].left, r, i<< 1 | 1, tag);
        return num1 + num2;
    }
}
signed main()
{
    ios::sync_with_stdio(false),cin.tie(0), cout.tie(0);
    cin >> total_num >> total_oper;
    for(int temp = 1 ; temp <= total_num ; temp++)
        cin >> arr[temp];
    Build(1,total_num,1);
    lli order, one,two,there;
    for(int temp = 0 ; temp < total_oper ; temp++){
        cin >> order;
        if(order == 1){
            cin >> one >> two >> there;
            modify(one,two,there,1);
        }else{
            cin >>one >> two;
            cout << query(one, two, 1, 0) << "\n";
        }
    }
    return 0;
}

Lazy-Tag (push_down版)

基本思路

在最开始的版本，我们要想知道一个区间确切的和需要上下两部分来完成

即该区间的sum值以及搜索该区间所途径的所有Lazy值得和

那么我们是否可以简化这一操作：

假设我们所途径得Lazy值均为0，那么我们求和就只需要一部分了

那么该如何让途径得Lazy为0呢

我们可以通过标记下方得方法让途径得Lazy值为0

但这个时候原本区间得sum值就不正确了

这个时候我们就需要对原本区间的sum值进行更新

简单的想一下会知道：原区间的确切和等于它两个子区间的确切和相加

那它两个子区间的确切和是啥呢

是该区间原本的和在加上Lazy标签的影响

建树

建树的代码跟普通的一致

//基本的准备

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli N = 100010;
lli arr[N];
struct Tree{
    lli sum, Lazy;
    lli left, right;
}seg[N << 2];

//建树

void Build(lli l, lli r, lli i){
    seg[i].left = l, seg[i].right = r, seg[i].Lazy = 0;
    if(l == r){
        seg[i].sum = arr[l];
        return ;
    }
    lli mid = (l + r) >> 1;
    Build(l, mid, i << 1);
    Build(mid + 1, r, i << 1 | 1);
    seg[i].sum = seg[i << 1].sum + seg[i << 1 | 1].sum;
}

区间修改

void Push_down(lli i, lli Lazy){ //这个函数是为了实现Lazy标签的下放
    seg[i << 1].Lazy += Lazy;
    seg[i << 1 | 1].Lazy += Lazy;
    seg[i].Lazy = 0;
}
void push_up(lli i){ //这个函数是为了将错误的sum修改回来
    lli one = seg[i<<1].sum + (seg[i<<1].right - seg[i << 1].left + 1)*seg[i << 1].Lazy;
    lli two = seg[i<<1|1].sum + (seg[i<<1|1].right - seg[i << 1|1].left + 1)*seg[i << 1|1].Lazy;
    seg[i].sum = one + two;
}
void modify(lli l, lli r, lli d, lli i){ //意义为：要修改区间的左端点，右端点，增加的数，结点编号
    if(seg[i].left == l && seg[i].right == r){
        seg[i].Lazy += d;
        return;
    }
    Push_down(i, seg[i].Lazy); //标签下放
    //分情况搜索
    if(seg[i << 1].right >= r) modify(l, r, d, i << 1);
    else if(seg[i << 1 | 1].left <= l) modify(l, r, d, i <<1 | 1);
    else{
        modify(l, seg[i << 1].right , d, i << 1);
        modify(seg[i << 1 | 1].left, r, d, i << 1 | 1);
    }
    push_up(i); // 更新sum值
}

区间查询

注意：

在区间查询的时候，搜索过程中肯定会遇到Lazy值不为0的情况

这个时候我们也要将标签下放

lli query(lli l, lli r, lli i){
    if(seg[i].left == l && seg[i].right == r)
        return seg[i].sum + seg[i].Lazy * (seg[i].right - seg[i].left + 1);
    Push_down(i, seg[i].Lazy);//下放
    lli ans = 0; //用于记录答案，不能直接return结果，因为还要更新sum
    if(seg[i << 1].right >= r) ans = query(l, r, i << 1);
    else if(seg[i << 1 | 1].left <= l) ans = query(l, r, i <<1 | 1);
    else{
        lli one = query(l, seg[i << 1].right , i << 1);
        lli two = query(seg[i << 1 | 1].left, r, i << 1 | 1);
        ans = one + two;
    }
    push_up(i);//更新
    return ans;
}

之前那一道模板题，用push_down优化后

P3372 【模板】线段树 1

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli N = 100010;
lli total_num, total_oper;
lli arr[N];
struct Tree{
    lli sum, Lazy;
    lli left, right;
}seg[N << 2];
void Build(lli l, lli r, lli i){
    seg[i].left = l, seg[i].right = r, seg[i].Lazy = 0;
    if(l == r){
        seg[i].sum = arr[l];
        return ;
    }
    lli mid = (l + r) >> 1;
    Build(l, mid, i << 1);
    Build(mid + 1, r, i << 1 | 1);
    seg[i].sum = seg[i << 1].sum + seg[i << 1 | 1].sum;
}
void Push_down(lli i, lli Lazy){
    seg[i << 1].Lazy += Lazy;
    seg[i << 1 | 1].Lazy += Lazy;
    seg[i].Lazy = 0;
}
void push_up(lli i){
    lli one = seg[i<<1].sum + (seg[i<<1].right - seg[i << 1].left + 1)*seg[i << 1].Lazy;
    lli two = seg[i<<1|1].sum + (seg[i<<1|1].right - seg[i << 1|1].left + 1)*seg[i << 1|1].Lazy;
    seg[i].sum = one + two;
}
void modify(lli l, lli r, lli d, lli i){
    if(seg[i].left == l && seg[i].right == r){
        seg[i].Lazy += d;
        return;
    }
    Push_down(i, seg[i].Lazy);
    if(seg[i << 1].right >= r) modify(l, r, d, i << 1);
    else if(seg[i << 1 | 1].left <= l) modify(l, r, d, i <<1 | 1);
    else{
        modify(l, seg[i << 1].right , d, i << 1);
        modify(seg[i << 1 | 1].left, r, d, i << 1 | 1);
    }
    push_up(i);
}
lli query(lli l, lli r, lli i){
    if(seg[i].left == l && seg[i].right == r)
        return seg[i].sum + seg[i].Lazy * (seg[i].right - seg[i].left + 1);
    Push_down(i, seg[i].Lazy);
    lli ans = 0;
    if(seg[i << 1].right >= r) ans = query(l, r, i << 1);
    else if(seg[i << 1 | 1].left <= l) ans = query(l, r, i <<1 | 1);
    else{
        lli one = query(l, seg[i << 1].right , i << 1);
        lli two = query(seg[i << 1 | 1].left, r, i << 1 | 1);
        ans = one + two;
    }
    push_up(i);
    return ans;
}
signed main()
{
    ios::sync_with_stdio(false),cin.tie(0), cout.tie(0);
    cin >> total_num >> total_oper;
    for(int temp = 1 ; temp <= total_num ; temp++)
        cin >> arr[temp];
    Build(1,total_num,1);
    lli order, one,two,there;
    for(int temp = 0 ; temp < total_oper ; temp++){
        cin >> order;
        if(order == 1){
            cin >> one >> two >> there;
            modify(one,two,there,1);
        }else{
            cin >>one >> two;
            cout << query(one, two, 1) << "\n";
        }
    }
    return 0;
}