动规之力扣矩阵类型动规

62.不同路径

定义dp数组，dp[i][j] 表示到点(i, j)的不同的路径数
到点 (i, j) 只有两条路，从左边走或者从上边走到该点，
所以可得

dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

那么我们再进行边界问题的判断
第一行和第一列的点只能从左边或者上边走到，所以均为1

    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; ++i) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; ++i) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }

64.最小路径和

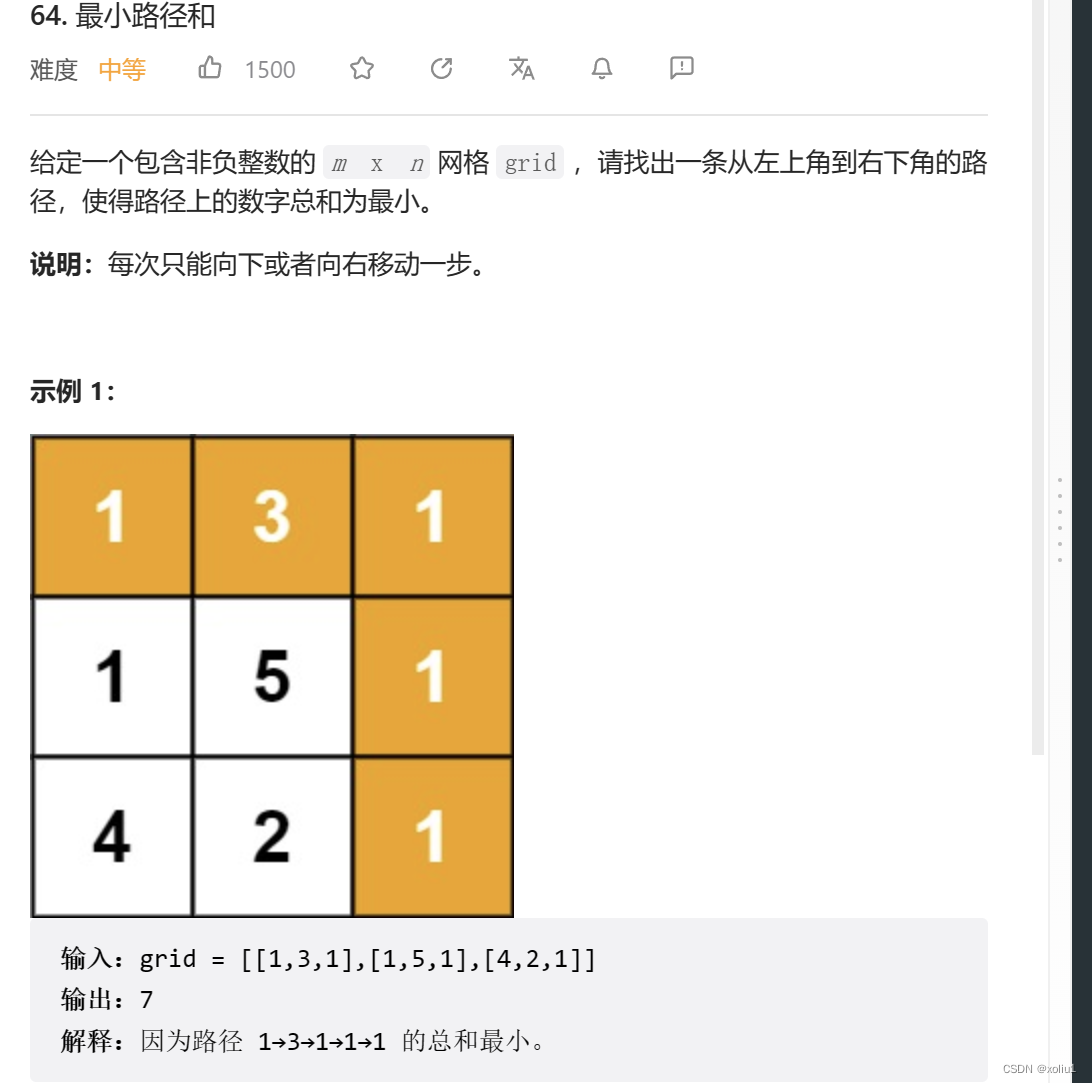
跟上题一样的行走方式，只能从左边或者上边来到这个点，可得转移方程：

dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];

处理边界问题的思考方式大同小异

故：

    public int minPathSum(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[][] dp = new int[row][col];
        //dp数组含义：dp[i][j]表示为，走到(i,j)的路径最小和
        //初始化
        //第0行和第0列，一定只能走一条线
        dp[0][0] = grid[0][0];
        for (int i = 1; i < row; ++i) {
            dp[i][0] = dp[i - 1][0] + grid[i][0]; 
        }
        for (int i = 1; i < col; ++i) {
            dp[0][i] = dp[0][i - 1] + grid[0][i];
        }
        //接下来填充剩余部分
        for (int i = 1; i < row; ++i) {
            for (int j = 1; j < col; ++j) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[row - 1][col - 1];
    }

63.不同路径Ⅱ

这道题的特点，就是出现了“障碍”，我们在原有的循环中，只需要进行判断是不是障碍，如果不是障碍，再进行状态转移

dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

边界问题，一旦出现障碍，后边的都无法通行，在这之前都一切正常

        for (int i = 1; i < row; ++i) {
            if (obstacleGrid[i][0] == 1) {
                break;//第一行障碍之后的都走不通
            }
            dp[i][0] = 1;
        }
        for (int i = 1; i < col; ++i) {
            if (obstacleGrid[0][i] == 1) {
                break;//同理
            }
            dp[0][i] = 1;
        }

故

    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        if (obstacleGrid[0][0] == 1 || obstacleGrid[obstacleGrid.length - 1][obstacleGrid[0].length - 1] == 1) {
            return 0;
        }
        if(obstacleGrid.length == 1 && obstacleGrid[0].length ==1 && obstacleGrid[0][0] == 0){
            return 1;
        }
        int row = obstacleGrid.length;
        int col = obstacleGrid[0].length;
        int[][] dp = new int[row][col];
        //dp数组含义：dp[i][j]表示为，走到(i,j)的路径数目
        //初始化
        //第0行和第0列，一定只能走一条线
        dp[0][0] = obstacleGrid[0][0];
        for (int i = 1; i < row; ++i) {
            if (obstacleGrid[i][0] == 1) {
                break;//第一行障碍之后的都走不通
            }
            dp[i][0] = 1;
        }
        for (int i = 1; i < col; ++i) {
            if (obstacleGrid[0][i] == 1) {
                break;//同理
            }
            dp[0][i] = 1;
        }
        //接下来填充剩余部分
        for (int i = 1; i < row; ++i) {
            for (int j = 1; j < col; ++j) {
                if (obstacleGrid[i][j] == 0) {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[row - 1][col - 1];
    }

931.下降路径最小和

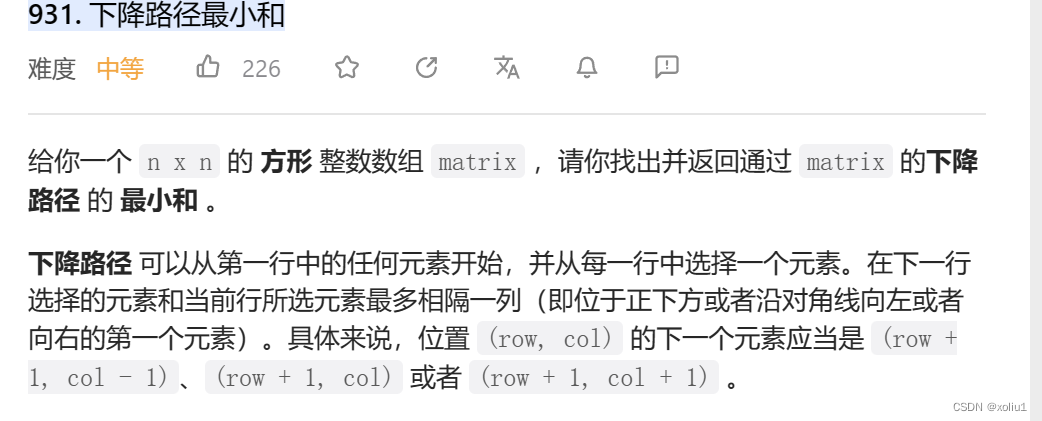
边界特殊判断 + 正常选择大小即可
最后我们看最后一行的最小值即为答案

    public int minFallingPathSum(int[][] matrix) {
        int size = matrix.length;
        //注意，第一行不用初始化
        //第一列和最后一列的数据所进行的比较很特殊
        for (int i = 1; i < size; ++i) {
            for (int j = 0; j < size; ++j) {
                if(j == 0){
                    matrix[i][j] = Math.min(matrix[i - 1][j], matrix[i - 1][j + 1]) + matrix[i][j];
                }else if(j == size - 1){
                    matrix[i][j] = Math.min(matrix[i - 1][j], matrix[i - 1][j - 1]) + matrix[i][j];
                }else{
                    matrix[i][j] = Math.min(matrix[i - 1][j], Math.min(matrix[i - 1][j + 1], matrix[i - 1][j - 1])) + matrix[i][j];
                }
            }
        }
        int mi = Integer.MAX_VALUE;
        for (int i = 0; i < size; ++i) {
            mi = Math.min(mi, matrix[size - 1][i]);
        }
        return mi;
    }

221. 最大正方形

• 我们定义dp[i][j]为以 (i, j)点为右下角的矩阵的包含(i, j)的最大正方形的边长

那么只要发现原矩阵中有dp[i][j] == 1，那么我们就能最起码确定这个正方形的边长 >= 1

• 可是这肯定不是最终的答案，我们需要把这个转换成已经推导过的值，也就是之前已经计算过的点。

再想，我们定义的dp[i][j] ,意思是将这个点当做最右下方的边界来看的，所以我们只能往左上方想。
如果这个点的最大正方形大于1,那么说明他的上边一点，左边一点，左上角的一点都脱不了干系，因为他们在一个正方形里，并且该点的边长肯定要比他们单个点确定的的正方形还要大1（它比他们更加靠近右下角）那么这个值如何确定呢？

如果三个值都相同，皆大欢喜；但是大部分都是不尽相同的，每个点对应的边长该取哪个？
我们需要取最小的那一个，这样每一个才能都得到满足，例如，上方的是最小的，我们取其他两个之一，都会无法构造正方形，但是取三个当中最小值，我们就能让所有的点都能套在这个正方形中。

这道问题的关键是我们可以从已经确定的小正方形去得到附近的正方形的值，因为正方形他的条件十分苛刻，就像一个木桶中最短的一块板子，我们光确定上边（dp[i - 1][j]）和左边（dp[i][j - 1]）是不够的，我们还要确定dp[i - 1][j - 1]是否可以。

换句话说，有三个相关的，①上边的点的最大正方形，②左边的点的最大正方形，③左上角的点的最大正方形。这三种情况是需要同时满足的，但①②③我们只能取最小值，就像那块最短的木板。

还有边界问题的思考

在第0行和第0列中，只有一行或者一列，如果某点为1，那么在以该点为结尾的正方形中，只能构造一个边长为1的正方形。

    public int maximalSquare(char[][] matrix) {
        if(matrix.length == 0 || matrix[0].length == 0){
            return 0;
        }
        int row = matrix.length;
        int col = matrix[0].length;
        int[][] dp = new int[row][col];
        int sideLength = 0;
        for (int i = 0; i < row; ++i) {
            for (int j = 0; j < col; ++j) {
                if(matrix[i][j] == '1'){
                    if(i == 0 || j == 0){
                        dp[i][j] = 1;
                    }else{
                        dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
                    }
                }else{
                    dp[i][j] = 0;
                }
                sideLength = Math.max(dp[i][j], sideLength);
            }
        }
        return sideLength * sideLength;
    }