数据结构：线性表

线性表

线性表的定义

由n（n>=0）个数据元素（结点）组成的有限序列，典型的线性结构

在非空线性表中：

• 有且仅有开始结点，没有直接前驱，而仅有一个直接后继

• 有且仅有终端结点，没有直接后继，而仅有一个直接前驱

• 其余内部结点都有且仅有一个直接前驱和直接后继

表长：数据元素的个数n（n=0时为空表）

两种方式：
SqList L SqList *L
L.elem L->elem

顺序存储结构

• 优点

随机存取，时间复杂度为O(1)

• 缺点

存储空间分配不灵活

运算的空间复杂度高

占用一片连续的存储空间

链式存储结构

• 优点

结点空间可以动态申请和释放

插入和删除不需要移动数据元素

• 缺点

指针域需额外占用存储空间

非随机存取结构，时间复杂度高

基本算法

InitList(): 构造一个空的线性表L

~InitList(): 销毁线性表

ClearList(): 将线性表重置为空表

ListEmpty(): 判断是否为空表，是返回Ture,否则返回False

ListLength(): 返回线性表中的数据元素个数

GetElem(i,&e): 返回线性表L中的第i个数据元素的值，1<=i<=ListLength()

PriorElem(cur,pre): 若cur是线性表的数据元素且不是第一个，则用pre返回它的前驱，否则pre无意义

NextElem(cur,next): 若cur是线性表的数据元素且不是最后一个，则用next返回它的后继，否则next无意义

ListTraverse(visited()): 依次对表中元素调用visited()，遍历

顺序表 ：

• 以物理位置相邻表示逻辑关系
• 任一元素均可以（随机存取）
• 插入删除时需移动大量元素，存储空间不灵活

顺序表的查找

平均查找长度：（n+1）/2
平均时间复杂度为O(n); 空间复杂度S(n)=O(1)

int LocateElem(e){   //返回线性表中e数据元素的位序 
  for(i=0;i<L.length;i++){
     if(L.elem==e) return i+1;  //查找成功返回序号
  }
  return 0;  //查找失败返回0
}

顺序表的插入

平均移动次数：n/2
平均时间复杂度为O(n); 空间复杂度S(n)=O(1)

ListInsert(i,e){  //在第i个位置之前插入新的数据元素e
   if(i<1||i>L.length)return ERROR;  //i值不合法
   for(j=L.length-1;j>=i-1;j--){
     L.elem[j+1]=L.elem[j];   //元素后移
   }
   L.elem[i-1]=e;
   L.length++;   //表长加一
   return OK;
}

顺序表的删除

平均移动次数：（n-1）/2
平均时间复杂度为O(n); 空间复杂度S(n)=O(1)

ListDelete(i,e){   //删除第i个位置数据元素，并用e返回其值
   if(i<1||i>L.length)return ERROR;  //i值不合法
   for(j=i;j<=L.length-1;j++){
     L.elem[j-1]=L.elem[j];   //元素前移
   }
   L.length--;    //表长减一
   return OK;
}

链表 ：

• n个结点由指针链组成一个链表
• 结点在存储器中位置是任意的
• 访问时只能通过头指针进入链表，并通过每个结点的指针域一次向后顺序扫描其余结点（顺序存取）
• 头指针—>（头结点）—>首元结点 [ 数据域data | 指针域next ]

单链表：一个指针域

双链表：两个指针域

循环链表：首尾结点相接

一. 单链表

class Node{
   int data;     //数据域
   Node *next;  //指针域
}

初始化单链表，销毁单链表，清空单链表

InitList(){    //初始化
   L=new Node;  
   L->next=NULL;
   return OK; 
}
DestroyList(){   //从头指针开始依次释放所有结点，销毁表
   Node *p;
   while(L){
      p=L;
      L=L->next;
      delete p;
   }
   return OK;
}
ClearList(){    //重置为空表
   Node *p,*q;
   p=L->next;
   while(p){
      q=p->next;
      delete p;
      p=q;
   }
   L->next=NULL;  //头结点指针域为空
   return OK;
}

判断链表是否为空

int ListEmpty(){
   if(L->next) return 0;   //非空
   else return 1;
}

求单链表的表长度

int ListLength(){   //返回数据元素个数
   Node *p;
   p=L->next;    //p指向第一个结点
   i=0;
   while(p){   //遍历
      i++;
      p=p->next;
   }
   return i;
}

取单链表中第i个元素的内容

GetElem(int i,int e){
   p=L->next;
   j=1;
   while(p&&j<i){  //向后扫描知道p指向第i个元素或p为空
      p=p->next;
      ++j;
   }
   if(!p||j>i) return ERROR;  //第i个元素不存在
   e=p->data;   //取第i个元素
   return OK;
}

单链表的查找

LacateElem(e){         //按值查找—返回该数据所在的位置（地址）
   p=L->next;
   while(p&&P->data!=e){
      p=p->next;
   }
   return p;
}
LacateElem(e){         //按值查找—返回该数据所在的位置（序号）
   p=L->next;
   j=1;
   while(p&&P->data!=e){
      p=p->next;
      j++;
   }
   if(p) return j;
   else return 0;
}

单链表的插入

在第i个结点前插入值为e的新结点

LinkInsert(i,e){
   p=L;j=0;
   while(p&&j<i-1){  //寻找第i-1个结点，p指向i-1结点
      p=p->next;  ++j;
   }
   if(!p||j>i-1) return ERROR;
   s=new Node;
   s->data=e;
   //链表插入重点
   s->next=p->next;
   p->next=s;
   //
   return OK;
}

单链表的删除

删除第i个结点,删除的值用e返回

LinkDelete(i){  //删除第i个数据元素
   p=L;j=0;
   while(p->next&&j<i-1){  //寻找第i个结点，并令p指向其前驱
      p=p->next;  ++j;
   }
   if(!(p->next)||j>i-1) return ERROR;
   q=p->next;    //临时保存被删结点的地址以备释放
   //链表删除重点：
   p->next=q->next; 
   e=q->data;    //保存删除结点的数据域
   //
   delete q;   //释放删除结点的空间
   return OK;
}

单链表的查找，插入，删除算法时间效率：时间复杂度：O(n)

建立单链表：

头插法：时间复杂度是O(n)

CreateList(int n){  //n为结点数
   L=new Node;
   L->next=NULL;
   for(i=n;i>0;--i){
      p=new Node;
      cin>>p->data;     //输入插入的数据
      p->next=L->next;  //插入到表头
      L->next=p;
   }
}

尾插法：时间复杂度为O(n)

CreateList(int n){  //n为结点数
   L=new Node; L->next=NULL;
   Node *r,*p;
   r=L;
   for(i=0;i<n;++i){
      cin>>p->data;  //输入结点元素值
      p->next=NULL;
      //插入到表尾
      r->next=p;
      r=p;
   }
}

二. 循环链表

从表中任一结点出发均可找到表中其他结点

循环链表中没有NULL指针，所有遍历终止条件不是判断p或p->next是否为空，而是判断是否等于头指针，即p!=L p->next!=L

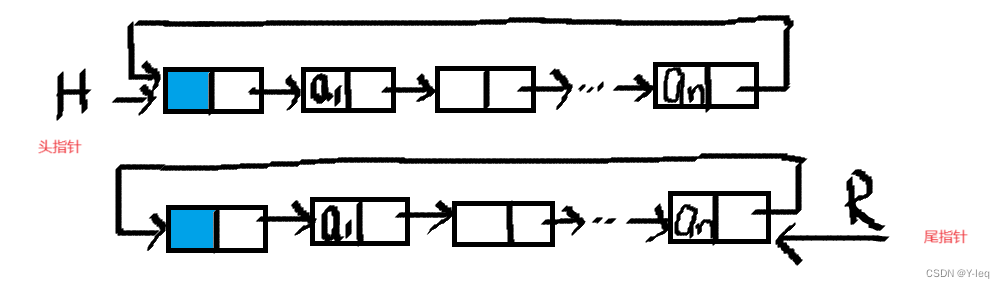
循环链表的合并：时间复杂度为O(1)

带尾指针的循环链表的合并（将Tb合并在Ta后）

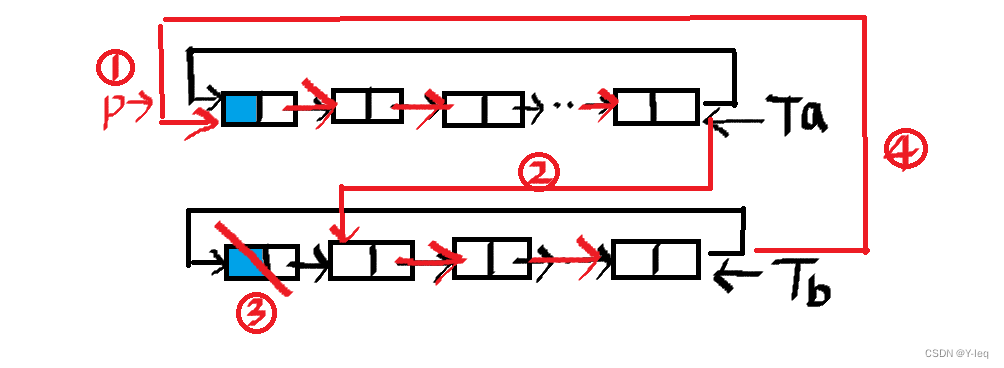
ConnectList(List Ta,List Tb){
   p=Ta->next;               //1 p存表头结点
   Ta->next=Tb->next->next； //2 Ta表尾连结Tb表头
   delete Tb->next；         //3 释放Tb头结点
   Tb->next=p；              //4 修改指针
   return Tb
}

三. 双向链表

class Node{ 
   int data;             //数据域
   Node *next，*prior;   //指针域
}

双向循环链表：

双向链表的插入

ListInsert(i,e){
   if(!(p=GetElem(L,i))) return ERROR;  //位置不合法
   s=new Node;  s->data=e;
   s->prior=p->prior;  p->prior->next=s;
   s->next=p;          p->prior=s;  
   return OK;
}

双向链表的删除

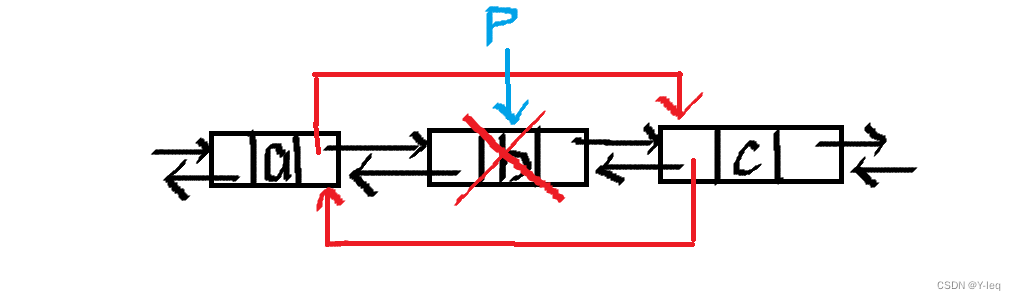
ListDelete(i,e){
   if(!(p=GetElem(L,i))) return ERROR;  //位置不合法
   e=p->data;
   p->prior->next=p->next;  
   p->next->prior=p->prior;
   delete p;
   return OK;
}

线性表的应用

线性表的合并

void union(List &La,List Lb){
   La_Len=Length(La); //获取两表的长度
   Lb_Len=Length(Lb);
   for(i=1;i<Lb_Len;i++){
      GetElem(Lb,i,e);   //取Lb表中元素值
      if(!LocateElem(La,e)){   
         Insert(&La,e);  //插入La
      }
   }
}

有序表的合并

【用顺序表实现】 时间和空间复杂度为O(length(La)+ length(Lb))

void UnionList(List La,List Lb,List &Lc){
   pa=La.elem;    //指针pa和pb初值分别指向两表中的第一个元素
   pb=Lb.elem;
   Lc.length=La.length+Lb.length;  //新表长度为待合并两表的长度之和
   Lc.elem=new int[Lc.length];     //为Lc分配一个数组空间
   pc=Lc.elem;
   pa_last=La.elem+La.length-1;   //pa_last指向La表中最后一个元素
   pb_last=Lb.elem+Lb.length-1;
   while(pa->pa_last && pb<=pb_last){  //两表都非空
       if(*pa<=*pb) *pc+=*pa++;  //依次取两表中值较小的结点
       else *pc+=*pb++;
   }
   while(pa<=pa_last) *pc+=*pa++; //Lb表到达表尾，则将La中剩余元素加入Lc
   while(pb<=pb_last) *pc+=*pb++;  //La表到达表尾，则将Lb中剩余元素加入Lc
}

【用链表实现】时间复杂度为O(length(La)+ length(Lb)) 空间复杂度O(1)

void UnionList(List &la,List &lb,List &lc){
    pa=La->next;  pb=Lb->next;
    pc=Lc=La;     //将La的头结点作为Lc的头结点
    while(pa && pb){
       if(pa->data<=pb->data)
          pc->next=pa; pc=pa; pa=pa->next;
       else
          pc->next=pb; pc=pb; pb=pb->next;
    }
    pc->next=pa?pa:pb;  //插入剩余段
    delete Lb;  //释放Lb的头结点
}

可运行代码：

#include <iostream>
using namespace std;
struct Node
{
    int data;
    Node* next;
};

class LinkList
{
    Node* first;
public:
    LinkList();
    LinkList(int a[], int n, int op);//建表,两种方法
    ~LinkList();
    int Length();
    int Get(int i);//按位置查找
    int Locate(int x);//按值查找
    void Insert(int i, int x);//在第i个位置插入数值x
    int Delete(int i);//删除第i个结点并返回第i个结点的值
    int Empty();
    void PrintList();
};

LinkList::LinkList()
{
    first = new Node;
    first->next = NULL;
}
LinkList::LinkList(int a[], int n, int op)
{
    //头插法
    if (op) {
        first = new Node;
        first->next = NULL;
        Node* s = NULL;
        for (int i = 0; i < n; i++) {
            s = new Node;
            s->data = a[i];
            s->next = first->next;
            first->next = s;
        }
    }
    //尾插法
    else {
        first = new Node;
        Node* tail = first, * s = NULL;
        for (int i = 0; i < n; i++) {
            s = new Node;
            s->data = a[i];
            tail->next = s;
            tail = s;
        }
        tail->next = NULL;
    }
}
LinkList::~LinkList()
{
    Node* p = NULL;
    while (first != NULL) {
        first = first->next;
        delete p;
        p = first;
    }
}
int LinkList::Length()
{
    Node* p = first->next;
    int cnt = 0;
    while (p != NULL) {
        p = p->next;
        cnt++;
    }
    return cnt;
}
int LinkList::Get(int i)
{
    Node* p = first->next;
    int cnt = 1;
    while (p != NULL && cnt < i) {
        p = p->next;
        cnt++;
    }
    if (p == NULL) cerr << "查找位置错误";
    return p->data;
}
int LinkList::Locate(int x)
{
    Node* p = first->next;
    int cnt = 1;
    while (p != NULL) {
        if (p->data == x)  return cnt;
        p = p->next;
        cnt++;
    }
    return 0;
}
void LinkList::Insert(int i, int x)
{
    Node* p = first, * s = NULL;
    int cnt = 0;
    while (p != NULL && cnt < i - 1) {
        p = p->next;
        cnt++;
    }
    if (p == NULL) cerr << "插入位置错误";
    else {
        s = new Node;
        s->data = x;
        s->next = p->next;
        p->next = s;
    }
}
int LinkList::Delete(int i)
{
    int x;
    Node* p = first, * q = NULL;
    int cnt = 0;
    while (p != NULL && cnt < i - 1) {
        p = p->next;
        cnt++;
    }
    if (p == NULL || p->next == NULL) cerr << "删除位置错误";
    else {
        q = p->next;
        x = q->data;
        p->next = q->next;
        delete q;
        return x;
    }
}
int LinkList::Empty()
{
    if (first->next == NULL) return 1;
    else return 0;
}
void LinkList::PrintList()
{
    Node* p = first->next;
    while (p != NULL) {
        cout << p->data << " ";
        p = p->next;
    }
    cout << endl;
}
int main()
{
    int r[5] = { 1,2,3,4,5 }, i, x;
    LinkList L(r, 5, 0);
    cout << "当前线性表的数据为: ";
    L.PrintList();
    try
    {
        L.Insert(2, 8);
        L.PrintList();
    }
    catch (string str) { cout << str << endl; }
    cout << "当前链表的长度为: " << L.Length() << endl;
    cout << "请输入查找的元素值: ";
    cin >> x;
    i = L.Locate(x);
    if (i > 0) cout << "元素" << x << "的位置为: " << i << endl;
    else cout << "单链表中没有元素" << x << endl;
    try
    {
        cout << "请输入要删除第几个元素: ";
        cin >> i;
        x = L.Delete(i);
        cout << "删除的元素值是" << x << ",执行删除操作后数据为: ";
        L.PrintList();
    }
    catch (string str) { cout << str << endl; }
    return 0;
};