最近学习了分页存储管理以及页面置换的相关知识,想要将所学内容进行自己的归纳总结,达到复习的目的
1.操作系统分页存储(paging)
分页是一种允许进程的物理地址空间非连续的内存管理方案。(逻辑地址空间中连续)
1.1基本方法
将物理内存分为固定大小的块,称为帧或页帧(frame);将逻辑内存分为同等大小的块,称为页或页面(page);页与页帧具有一一对应的关系。
分页的硬件支持如下:

由CPU生成的地址包含两部分:页码(page number)(p),页偏移(page offset)(d)。页码是页表(page table)的索引 。通过页表可将逻辑地址转变为物理地址储存在物理内存之中。可以看出分页是一种动态的重定位,逻辑地址通过重定位寄存器绑定到物理地址中。
1.1.1 外部碎片 内部碎片 分页存储
补充外部碎片以及内部碎片的概念:
外部碎片:内存中某些空闲分区太小无法被利用。
内部碎片:分配给某进程的内存区域中,有没有被使用的区域。
因为分页存储是将内存分为一块块相同大小的区域,所以不存在外部碎片,但是存在内部碎片。
2.三种页面置换算法(page replacement)
好的页面算法应追求更低的缺页率。
以下为所展示代码所需的头文件以及一些全局变量
#include<iostream>
#include<queue>
using namespace std;
int arr[100];
int page[100];
int pageSize = 3, addrSize;
bool bre;以下为所需要用到的一些函数:
bool isEqual(queue<int> que, int num)
{
while (!que.empty())//遍历队列,查看是否页已存在
{
if (que.front() == num)
return true;
que.pop();
}
return false;
}
void print(queue<int> que, int p)//打印
{
cout << "调用的页面为:" << p;
if (bre)
cout << " 产生中断: ";
else
cout << " 不产生中断: ";
while (!que.empty())
{
cout << que.front() << " ";
que.pop();//输出物理块中页号
}
cout << endl;
}2.1 FIFO 页面置换算法
FIFO(first in first out) 即先进先出的页面置换算法,就是在没有空闲帧的情况下,将最先占有的帧释放,再从所需页面中读入新的空闲帧。
FIFO算法是最简单的页面置换算法,以下为部分代码:(假设物理块数为3,页面大小为100单元)
void FIFO()//first in first out
{
int queye = 1, i;
cout << "FIFO" << endl;
queue<int> que;
que.push(page[0]);//第一页一定产生缺页
bre = true;
print(que, page[0]);
for (i = 1; i < addrSize; i++)//从第二页开始判断是否缺页
{
if (!isEqual(que, page[i]))//若队列中不存在
{
bre = true;//发生缺页
if (que.size() < 3)//若物理块未满,则直接将新页加入队列
{
que.push(page[i]);
queye++;
}
else//若物理块已满。根据fifo将队首弹出,队尾插入新页
{
que.pop();
que.push(page[i]);
queye++;//queye记录缺页中断次数
}
print(que, page[i]);
}
else//若队列中已存在页面,则不会产生缺页中断
{
bre = false;
print(que, page[i]);
}
}
double queyelv = (double)queye / (double)addrSize;//缺页率为:缺页中断次数/访问页面数
cout << "缺页率:" << queyelv << endl;
}该算法非常的简洁明了,利用队列的先进先出特性进行编写。页面按照使用顺序写入队列之中,这个队列可看做物理块,在新页面到来时通过判断队列中是否存在该页面和是否有空闲位置来选择是否置换页面,发生缺页中断。使用变量queye来记录缺页次数。、
2.1.2 不足之处
FIFO算法会出现一种特殊的现象,即分配更多的物理块时,反而会出现更多的缺页中断。
我们将这种异常情况称为Belady异常
2.2 OPT置换算法
OPT置换算法即最有页面置换算法。这个算法具有所有算法中的最低的缺页率。
该算法的行为是将时间向前看,通过置换最长时间不会被使用的页面来达成目的。这样可以减少需重复利用页面的换入换出,从而减少缺页次数,但是这种置换算法是很难被实现的。因为他需要知道所有页面的到达顺序,而这往往是很难预知的。因此,我们将OPT算法作为一种标杆,来研究其他算法的优良性。以下为实现OPT算法的操作以及所需函数:
这是队列更新的函数,目的是置换最长时间不会被使用的页面。
queue<int> OPT_update(queue<int> que, int insert_element, int remove_element)
{
queue<int> que1;
while (!que.empty())
{
if (que.front() != remove_element)//若不为需要被置换的页,则进入新队列
que1.push(que.front());
que.pop();//若需要被置换,则直接离开队列
}
que1.push(insert_element);//放入新的页
return que1;
}这个函数用来查找最长时间不会被使用的页面(通过比较距离)
int select_most_far(int index, queue<int> que)//查找之后最远要使用或不再使用的页
{
int a = que.front();//若队列已满,将队列中的页存起来
que.pop();
int b = que.front();
que.pop();
int c = que.front();
int dis1 = 10000000, dis2 = 10000000, dis3 = 10000000, i, max;
index++;
for (i = index; i < addrSize; i++)//三次循环分别找到三个页下一次使用的距离
{
if (page[i] == a)
{
dis1 = i - index;
break;
}
}
for (i = index; i < addrSize; i++)
{
if (page[i] == b)
{
dis2 = i - index;
break;
}
}
for (i = index; i < addrSize; i++)
{
if (page[i] == c)
{
dis3 = i - index;
break;
}
}
int result;
if (dis1 > dis2)//比大小选出最远的进行替换
{
max = dis1;
result = a;
}
else
{
max = dis2;
result = b;
}
if (max > dis3)
return result;
else
return c;
}OPT置换算法:
void OPT()//最优页面置换算法
{
int queye = 1;
cout << "OPT" << endl;
queue<int> que;
que.push(page[0]);
bre = true;
print(que, page[0]);
for (int i = 1; i < addrSize; i++)
{
if (!isEqual(que, page[i]))//队列中不存在要使用的页
{
bre = true;
if (que.size() >= 3)//物理块已占满
{
int remove_element = select_most_far(i, que);//找到最远使用页
que = OPT_update(que, page[i], remove_element);//新页替换最远使用页
print(que, page[i]);
}
else
{
que.push(page[i]);
print(que, page[i]);
}
queye++;
}
else
{
bre = false;
print(que, page[i]);
}
}
double queyelv = (double)queye / (double)addrSize;
cout << "缺页率:" << queyelv << endl;
}该算法也较容易理解,在物理块满且不存在要使用的页面时来查找该物理块中最长时间不会再被使用的页面 并将之移除队列。
2.3 LRU置换算法
LRU(Least-Recently-Used)最近最少使用算法。这种算法是将每个页面和他的上次使用时间关联起来。这种策略可当做在时间上向后看而非向前看的最优置换算法(OPT算法)。
该算法的相关函数:
队列更新的函数:
每次都将最新使用的页面放入队尾,将最久未被使用的页面放入队首,方便进行移除队列的操作。
queue<int> LRU_update(queue<int> que, int num)//使用队列更新
{
queue<int> que1;//创建新队列
while (!que.empty())
{
if (que.front() != num)//若队首不为新加入的页(即未被使用)
{
que1.push(que.front());//将旧队列的队首插入新队列中
}
que.pop();
}
que1.push(num);//将新加入的页放入新队列队尾
return que1;//返回新队列
}LRU的实现函数:
void LRU()//Least-Recently-Used 最近最少使用
{
int queye = 1, i;
cout << "LRU" << endl;
queue<int> que;
que.push(page[0]);
bre = true;
print(que, page[0]);
for (i = 1; i < addrSize; i++)
{
if (!isEqual(que, page[i]))//没有相同的页
{
bre = true;
if (que.size() < 3)
{
que.push(page[i]);
queye++;
}
else//若队满
{
que.pop();//将队首弹出,根据算法可得出每次队首都是最近最少使用的页
que.push(page[i]);
queye++;
}
print(que, page[i]);
}
else//新队列中有相同的页
{
bre = false;
que = LRU_update(que, page[i]);//队列更新(将再次使用的页放入新队列队尾)
print(que, page[i]);
}
}
double queyelv = (double)queye / (double)addrSize;
cout << "缺页率:" << queyelv << endl;
}每次更新队列都是将页面从就队列中移入新队列的过程,若队首页面不为新加入页面则将之仍然放在新队列的队首, 在物理块达到上限后将其移除队列,并加入新页面。若队首页面为新页面,则在转换新队列时将其从就队列中移除并在最后插入到新队列的队尾。如此一来,可以保证每次进入的新页面都在队尾,而队首都是最长时间未被使用的页面,就达到了LRU的目的。
3.程序main函数的实现以及运行结果:
int main()
{
int i, select;
bool judge = true;
cout << "输入地址总数和地址序列:" << endl;
cin >> addrSize;
for (i = 0; i < addrSize; i++)
{
cin >> arr[i];
page[i] = arr[i] / 100 + 1;//假设页面大小是100单元
}
while (judge)
{
cout << "1:FIFO" << endl;
cout << "2:LRU" << endl;
cout << "3:OPT" << endl;
cin >> select;
switch (select)
{
case 1:FIFO();
break;
case 2:LRU();
break;
case 3:OPT();
break;
}
}
return 0;
}运行过程:

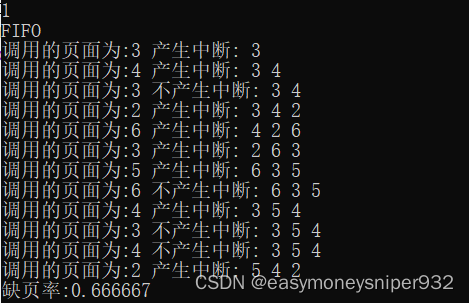
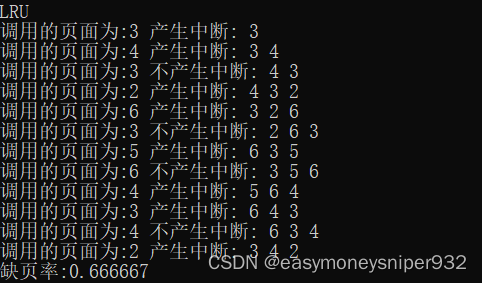







 本文详细介绍了分页存储管理的概念,包括其基本方法、外部碎片和内部碎片,以及FIFO、OPT和LRU三种页面置换算法的工作原理、优缺点和实现。通过示例代码展示了如何在程序中应用这些算法,以及它们对缺页率的影响。
本文详细介绍了分页存储管理的概念,包括其基本方法、外部碎片和内部碎片,以及FIFO、OPT和LRU三种页面置换算法的工作原理、优缺点和实现。通过示例代码展示了如何在程序中应用这些算法,以及它们对缺页率的影响。

















 5866
5866

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








