目录
(2)知道加密后的文本和公钥文本(就是知道了n、p、q、e、c求m)
(一)古典密码
1.摩斯密码
有时候一串101010可能代表的是-.-.-.

2.移位密码
(1)凯撒密码
密码统一移动几位
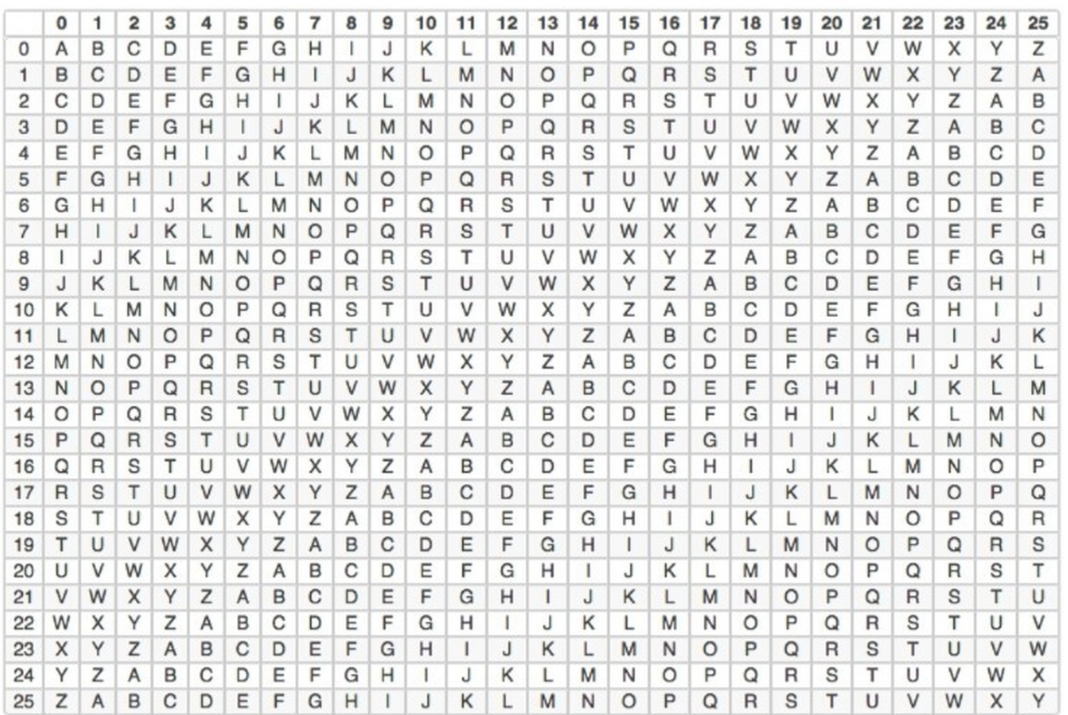
(2)栅栏密码
①常规型
栅栏密码是一种相对简单但又具有一定保密性的加密方法。它的原理是将明文按照一定的行数写成栅栏状,然后按列读取得到密文。例如,明文“HELLO WORLD”设定行数为2,写成栅栏状为:
H L O R E L W D
按列读取得到密文“HLOR ELWD
②W型
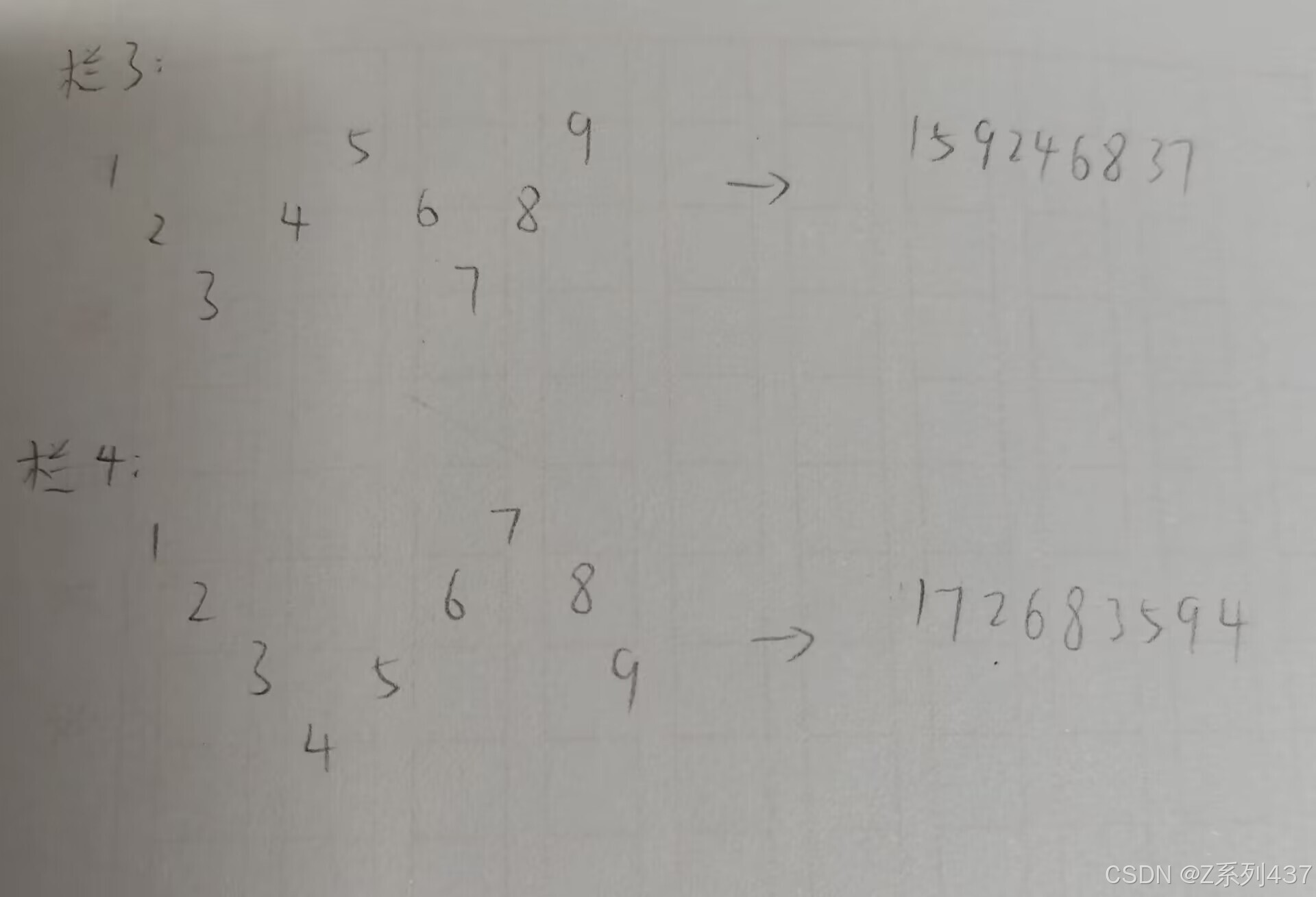
(3)曲路密码

(4)列移位
举例: 明文:The quick brown fox jumps over the lazy dog 密钥:how are u

密文:qoury inpho Tkool hbxva uwmtd cfseg erjez
(5)rot13
就是凯撒密码偏移量为13的情况
3.替换密码
(1)行置换密码
加密

解密

(2)棋盘密码

明文 HELLO,加密后就是 23 15 31 31 34
(3)vigenere维吉尼亚密码

(4)培根密码

(5)猪圈密码

(6)键盘密码
①电脑键盘

例如:11为Q,23为D
②键盘围成的密码
例如:xrv为c
(7)盲文密码

(8)幂数加密/云影密码

(9)brainfuck
++++++++++[>+++++++>++++++++++>+++>+<<<<-] ++.>+.+++++++…+++.>++.<<+++++++++++++++. .+++.------.--------.>+.>.
(10)Ook
#-*-coding:utf-8-*-
import sys
from collections import deque
class LoopError(Exception):
pass
class OokParser(object):
def __init__(self):
self.BEGIN = ('!', '?')
self.END = ('?', '!')
self.primitives = {('.', '.'): 'inc',
('!', '!'): 'dec',
('.', '?'): 'right',
('?', '.'): 'left',
('!', '.'): 'write',
('.', '!'): 'read'}
def parse(self, input_text):
items = input_text.lower().replace('ook','').replace(' ', '').replace('\n','').replace('\r','')
for i in range(0, len(items), 2):
x = (items[i], items[i+1])
if x in self.primitives or x in (self.BEGIN, self.END):
yield x
class BrainfuckParser(object):
def __init__(self):
self.BEGIN = '['
self.END = ']'
self.primitives = {'+': 'inc',
'-': 'dec',
'>': 'right',
'<': 'left',
'.': 'write',
',': 'read'}
def parse(self, input_text):
for x in input_text:
if x in self.primitives or x in (self.BEGIN, self.END):
yield x
class Interpreter(object):
MAX_NESTED_LOOPS = 1000
def __init__(self, ook_mode=True):
self.bf_parser = BrainfuckParser()
self.ook_parser = OokParser()
self.set_parser(ook_mode and self.ook_parser or self.bf_parser)
def reset(self):
self.cells = deque([0])
self.index = 0
self.input_buffer = []
self.output_buffer = []
self.open_loops = 0
self.loop = []
def inc(self):
self.cells[self.index] += 1
def dec(self):
self.cells[self.index] -= 1
def right(self):
self.index += 1
if self.index >= len(self.cells):
self.cells.append(0)
def left(self):
if self.index == 0:
self.cells.appendleft(0)
else:
self.index -= 1
def write(self):
self.output_buffer.append(self.cells[self.index])
def read(self):
try:
self.cells[self.index] = int(raw_input("Your input: "))
except (TypeError, ValueError):
print ("Invalid input! Continuing ...")
def as_ascii(self):
return "".join([chr(c) for c in self.output_buffer])
def set_parser(self, parser):
self.parser = parser
self.reset()
def interpret_raw_text(self, text):
self.input_buffer.extend(self.parser.parse(text))
try:
self.interpret_items(self.input_buffer)
except IndexError:
print (" ... (incomplete)")
except LoopError:
print ("LoopError ... exiting")
sys.exit(1)
def interpret_items(self, items):
for item in items:
if self.open_loops:
self.interpret_inside_loop(item)
else:
self.interpret_directly(item)
def interpret_inside_loop(self, item):
if item == self.parser.END:
self.open_loops -= 1
if self.open_loops == 0:
while self.cells[self.index]:
self.interpret_items(self.loop)
return
elif item == self.parser.BEGIN:
if self.open_loops < self.MAX_NESTED_LOOPS:
self.open_loops += 1
else:
raise LoopError("Nesting maximum (%s) exceeded"
% self.MAX_NESTED_LOOPS)
self.loop.append(item)
def interpret_directly(self, item):
if item == self.parser.END:
raise ValueError("End without begin")
elif item == self.parser.BEGIN:
self.open_loops = 1
self.loop = []
elif item in self.parser.primitives:
method = self.parser.primitives[item]
getattr(self, method)()
else:
print ("Unknown token '%s' - ignored") % (item, )
def interpret_file(self, fname):
file = open(fname, 'r')
self.interpret_raw_text(file.read())
def interactive_mode(self):
print ("Ook! and Brainfuck interpreter V1.0")
print ("Type '?' to display the status of the interpreter. ")
print ("Type 'b' to enter brainfuck mode. Empty input quits.")
while True:
inp = raw_input("oo> ").strip()
if inp == "?":
print (self)
elif inp == "b":
print ("Entering brainfuck mode. Type 'o' to return to Ook!")
self.set_parser(self.bf_parser)
elif inp == "o":
print ("Entering Ook! mode. Type 'b' to return to brainfuck.")
self.set_parser(self.ook_parser)
elif inp == "":
print (self)
break
else:
self.interpret_raw_text(inp)
def __repr__(self):
rep = "\n".join(["Cells\t\t: %s",
"Raw output\t: %s",
"ASCII output\t: %s"])
return rep % (list(self.cells),
" ".join([str(i) for i in self.output_buffer]),
self.as_ascii())
def print_usage():
print ("\nUsage:")
print ("\tInterpret Ook! : python ook.py -o <FILENAME>")
print ("\tInterpret BrainFuck : python ook.py -b <FILENAME>")
print ("\tInteractive mode: python ook.py -i\n")
if __name__ == '__main__':
if len(sys.argv) < 2:
print_usage()
elif len(sys.argv) == 2 and sys.argv[1] == "-i":
ook = Interpreter()
ook.interactive_mode()
elif len(sys.argv) == 3:
if sys.argv[1] == "-b":
ook = Interpreter(ook_mode=False)
ook.interpret_file(sys.argv[2])
print (ook)
elif sys.argv[1] == "-o":
ook = Interpreter(ook_mode=True)
ook.interpret_file(sys.argv[2])
print (ook)
else:
print_usage()
else:
print_usage()
(11)标准银河字母

(12)简单替换密码

(二)编码
1.ASCII编码

2.Base编码
base64、32、16。。。
3.unicode编码
源文本: The &#x [Hex]: The &# [Decimal]: The \U [Hex]: \U0054\U0068\U0065 \U+ [Hex]: \U+0054\U+0068\U+0065
4.url编码
例子:The quick %54%68%65%20%71%75%69%63%6b
5.html编码
(1)普通html编码
特征:&# 开头 由 &# 开头,后面加数字
(2)html实体编码

6.rabbit编码
跟base64很像,但是需要密钥,Rabbit加密开头部分通常为U2FsdGVkX1
7.python反编译
EasyPythonDecompiler软件,1.pyc转1.py
8.quipquip词频分析
(三)现代密码学--对称加密
1.DES
2.AES
3.RC4
RC4包含两个算法: 1.密钥调度算法(KSA) 2.伪随机数生成算法(PRGA)
RC4是经典流密码之一,由于加密和解密使用相同的密钥,所以也是对称密码的一种。由于RC4存在弱点,现已禁止在TLS中使用RC4加解密算法。
RC4会根据明文长度将密钥扩展到与明文相同的长度,并遵从逐个字节加密的原则。加密的原理是异或。
def rc4_init(s_box, key, key_len): # rc4初始化函数,产生s_box k = [0] * 256 i = j = 0 for i in range(256): s_box[i] = i k[i] = key[i % key_len] for i in range(256): j = (j + s_box[i] + ord(k[i])) % 256 s_box[i], s_box[j] = s_box[j], s_box[i] def rc4_crypt(s_box, data, data_len, key, key_len): # rc4算法,由于异或运算的对合性,RC4加密解密使用同一套算法,加解密都是它 rc4_init(s_box, key, key_len) i = j = 0 for k in range(data_len): i = (i + 1) % 256 j = (j + s_box[i]) % 256 s_box[i], s_box[j] = s_box[j], s_box[i] t = (s_box[i] + s_box[j]) % 256 data[k] ^= s_box[t] if __name__ == '__main__': s_box = [0] * 257 # 定义存放s_box数据的列表 # 此处的data即要解密的密文,需要定义成列表形式,其中的元素可以是十六进制或十进制数 # 如果题目给出的是字符串,需要你自己先把数据处理成列表形式再套用脚本 data = [0xB6,0x42,0xB7,0xFC,0xF0,0xA2,0x5E,0xA9,0x3D,0x29,0x36,0x1F,0x54,0x29,0x72,0xA8,0x63,0x32,0xF2,0x44,0x8B,0x85,0xEC,0xD,0xAD,0x3F,0x93,0xA3,0x92,0x74,0x81,0x65,0x69,0xEC,0xE4,0x39,0x85,0xA9,0xCA,0xAF,0xB2,0xC6] #key一定要字符串 key = "gamelab@" rc4_crypt(s_box, data, len(data), key, len(key)) for i in data: print(chr(i), end='')
(四)现代密码学--非对称加密
1.RSA


(1)基础已知p、q、e求d
#RSA---知道p、q、e求d
from Crypto.Util.number import *
#gmpy2 是一个用于高精度数学运算的 Python 库,它提供了快速的大整数运算功能
import gmpy2
# 定义素数 p 和 q
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
# 计算模数 n
n = p * q
# 计算欧拉函数 φ(n)
r = (p - 1) * (q - 1)
# 选择公钥指数 e
e = 65537
# 计算私钥指数 d
d = gmpy2.invert(e, r)
# 打印私钥指数 d
print("私钥指数 d:", d)
(2)知道加密后的文本和公钥文本(就是知道了n、p、q、e、c求m)

step1:使用openssl解出e和n
openssl rsa -pubin -text -modulus -in warmup -in pubkey.pem

e=65537,n=Modulus的十六进制
step2:进制转换(16转10)
def hex_to_decimal(hex_string):
try:
decimal_num = int(hex_string, 16)
return decimal_num
except ValueError:
print("输入的不是有效的十六进制字符串。")
return None
hex_str = "C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD"
result = hex_to_decimal(hex_str)
if result is not None:
print(f"转换为十进制是: {result}")
n=87924348264132406875276140514499937145050893665602592992418171647042491658461
step3:使用yafu分解n,得出p、q

step4:加密后的文本flag.enc的十六进制再转为十进制就是c


c=49412914049026066227292604633959399022586841904231599586841156187258952420473
step5:根据基础ras脚本解出m
from Crypto.Util.number import * import gmpy2 e=65537 p= 319576316814478949870590164193048041239 q= 275127860351348928173285174381581152299 n=p*q c = 49412914049026066227292604633959399022586841904231599586841156187258952420473 r=(p-1)*(q-1) d=gmpy2.invert(e,r) m=pow(c,d,n) print(m)
得到m=4865677769286717240419296208145914517832094464845949055035370987525602570
step6:m转为16进制,再转为ASCII码(这样更不容易出错,有些题会出现多一个字符的情况)
def decimal_to_hex(decimal_num):
hex_chars = "0123456789ABCDEF"
if decimal_num == 0:
return '0'
hex_str = ''
negative = False
if decimal_num < 0:
negative = True
decimal_num = -decimal_num
while decimal_num > 0:
remainder = decimal_num % 16
hex_str = hex_chars[remainder] + hex_str
decimal_num //= 16
if negative:
hex_str = '-' + hex_str
return hex_str
decimal_num =4865677769286717240419296208145914517832094464845949055035370987525602570
hex_result = decimal_to_hex(decimal_num)
print(f"转换为十六进制是: {hex_result}")

这种情况是多了一位,删去2

(3)知道加密后的文本和私钥文本
openssl rsautl -decrypt -in key.txt(加密后的文件) -inkey pub.key(私钥) -out flag.txt
(4)RSA共模攻击
所谓共模,就是明文m相同,模n相同,用两个公钥e1,e2加密得到两个私钥d1,d2和两个密文c1,c2 共模攻击,即当n不变的情况下,知道n,e1,e2,c1,c2 。可以在不知道d1,d2的情况下,解出m
import gmpy2 n=13060424286033164731705267935214411273739909173486948413518022752305313862238166593214772698793487761875251030423516993519714215306808677724104692474199215119387725741906071553437840256786220484582884693286140537492541093086953005486704542435188521724013251087887351409946184501295224744819621937322469140771245380081663560150133162692174498642474588168444167533621259824640599530052827878558481036155222733986179487577693360697390152370901746112653758338456083440878726007229307830037808681050302990411238666727608253452573696904083133866093791985565118032742893247076947480766837941319251901579605233916076425572961 c1=12847007370626420814721007824489512747227554004777043129889885590168327306344216253180822558098466760014640870748287016523828261890262210883613336704768182861075014368378609414255982179769686582365219477657474948548886794807999952780840981021935733984348055642003116386939014004620914273840048061796063413641936754525374790951194617245627213219302958968018227701794987747717299752986500496848787979475798026065928167197152995841747840050028417539459383280735124229789952859434480746623573241061465550303008478730140898740745999035563599134667708753457211761969806278000126462918788457707098665612496454640616155477050 c2=6830857661703156598973433617055045803277004274287300997634648800448233655756498070693597839856021431269237565020303935757530559600152306154376778437832503465744084633164767864997303080852153757211172394903940863225981142502888126928982009493972076013486758460894416710122811249903322437742241269681934551237431668187006176418124934488775505816544733929241927900392924886649420943699356314278255683484998359663404611236056664149725644051300950988495549164517140159041907329062655574220869612072289849679613024196448446224406889484578310512232665571188351621585528255501546941332782446448144033997067917984719103068519 e1=117 e2=65537 r,s1,s2 = gmpy2.gcdext(e1, e2) m = (pow(c1,s1,n)*pow(c2,s2,n)) % n print(m)
(5)分解素数多于两个
攻防世界:baigeiRSA2
step1:分解n,素数为5个

step2:脚本
from Crypto.Util.number import * import gmpy2 e=65537 p=9401433281508038261 q=13716847112310466417 s=11215197893925590897 t=11855687732085186571 y=10252499084912054759 n=p*q*s*t*y c =144009221781172353636339988896910912047726260759108847257566019412382083853598735817869933202168 r=(p-1)*(q-1)*(s-1)*(t-1)*(y-1) d=gmpy2.invert(e,r) m=pow(c,d,n) print(m)
大体都一样,就是n=pqsty,r=(p-1)(q-1)(s-1)(t-1)(y-1),这两个地方变了
(6)n分解出来就一个(即n是质数)
from Crypto.Util.number import * import gmpy2 e=65537 p= 2277984791022346369005533904783614818826102788659651508959767202083843778453131366658916382803461140562467908905967443285040501371560088604538394878005827646410146244954745505114406792711000349929611271710262426493710967674490536959788665890671796421985910748091011210709414415838780453626144971988788672588103654983 n=p c = 415510106371698055042355817455792784402467839071261284227679808181073943762112386236619891503158397068812942349049185918370823556100880803528976860244812587012654626659823858350868438615582709075400040571632681052556974452098591809573228654622307014559692352778252371646024960520522510301144376842967556042367321117 r=(p-1) d=gmpy2.invert(e,r) m=pow(c,d,n) print(m)
大体都一样,就是n=p,r=p-1
2.DH
3.ECC
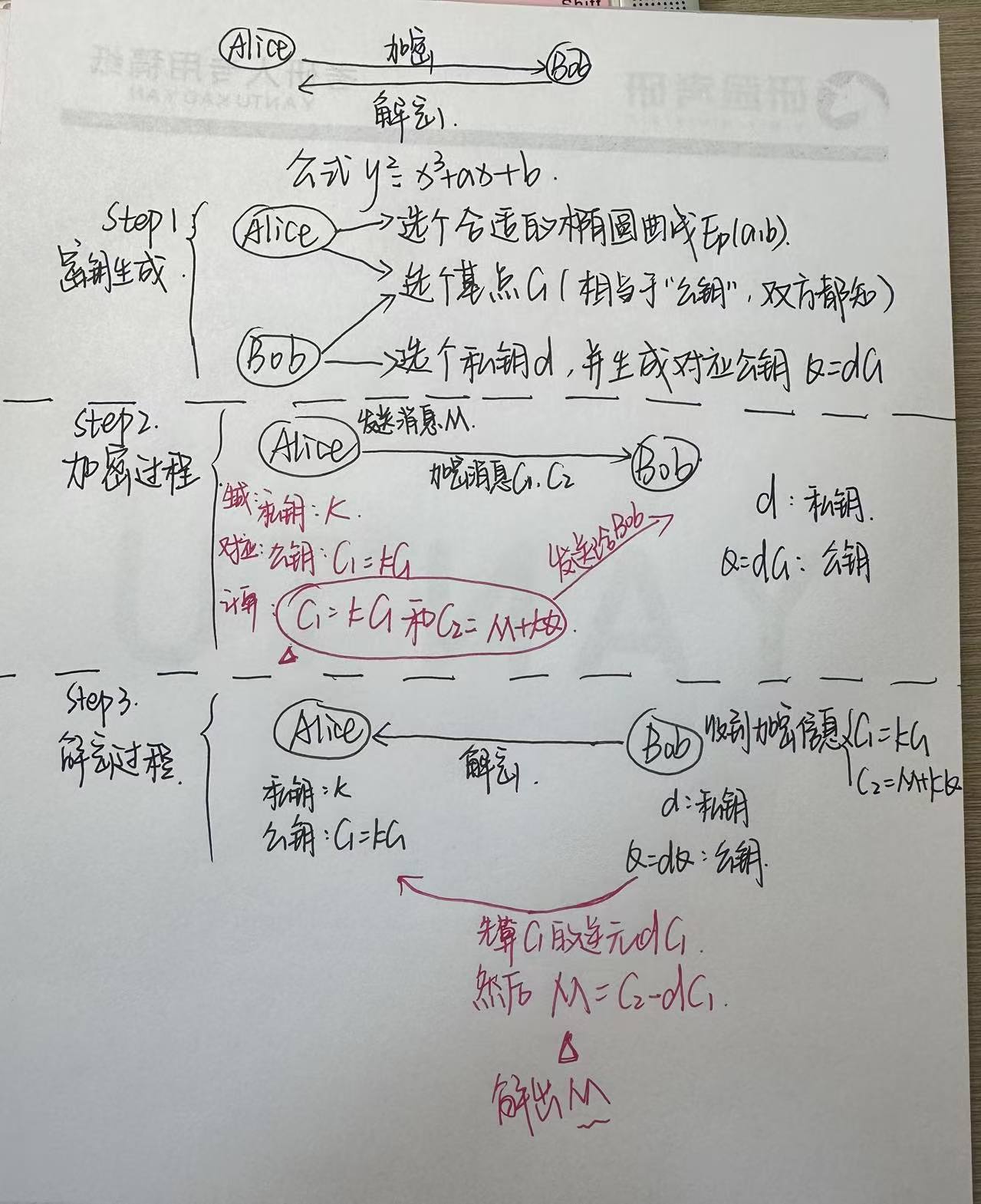
(1)椭圆曲线加密基础
知道p(有限特征值)、a、b、G(基点)、k(私钥),求公钥K,也就是上图的C1
import collections
import random
EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
curve = EllipticCurve(
'secp256k1',
# Field characteristic.
p=int(input('p=')),
# Curve coefficients.
a=int(input('a=')),
b=int(input('b=')),
# Base point.
g=(int(input('Gx=')),
int(input('Gy='))),
# Subgroup order.
n=int(input('k=')),
# Subgroup cofactor.
h=1,
)
# Modular arithmetic ##########################################################
def inverse_mod(k, p):
"""Returns the inverse of k modulo p.
This function returns the only integer x such that (x * k) % p == 1.
k must be non-zero and p must be a prime.
"""
if k == 0:
raise ZeroDivisionError('division by zero')
if k < 0:
# k ** -1 = p - (-k) ** -1 (mod p)
return p - inverse_mod(-k, p)
# Extended Euclidean algorithm.
s, old_s = 0, 1
t, old_t = 1, 0
r, old_r = p, k
while r != 0:
quotient = old_r // r
old_r, r = r, old_r - quotient * r
old_s, s = s, old_s - quotient * s
old_t, t = t, old_t - quotient * t
gcd, x, y = old_r, old_s, old_t
assert gcd == 1
assert (k * x) % p == 1
return x % p
# Functions that work on curve points #########################################
def is_on_curve(point):
"""Returns True if the given point lies on the elliptic curve."""
if point is None:
# None represents the point at infinity.
return True
x, y = point
return (y * y - x * x * x - curve.a * x - curve.b) % curve.p == 0
def point_neg(point):
"""Returns -point."""
assert is_on_curve(point)
if point is None:
# -0 = 0
return None
x, y = point
result = (x, -y % curve.p)
assert is_on_curve(result)
return result
def point_add(point1, point2):
"""Returns the result of point1 + point2 according to the group law."""
assert is_on_curve(point1)
assert is_on_curve(point2)
if point1 is None:
# 0 + point2 = point2
return point2
if point2 is None:
# point1 + 0 = point1
return point1
x1, y1 = point1
x2, y2 = point2
if x1 == x2 and y1 != y2:
# point1 + (-point1) = 0
return None
if x1 == x2:
# This is the case point1 == point2.
m = (3 * x1 * x1 + curve.a) * inverse_mod(2 * y1, curve.p)
else:
# This is the case point1 != point2.
m = (y1 - y2) * inverse_mod(x1 - x2, curve.p)
x3 = m * m - x1 - x2
y3 = y1 + m * (x3 - x1)
result = (x3 % curve.p,
-y3 % curve.p)
assert is_on_curve(result)
return result
def scalar_mult(k, point):
"""Returns k * point computed using the double and point_add algorithm."""
assert is_on_curve(point)
if k < 0:
# k * point = -k * (-point)
return scalar_mult(-k, point_neg(point))
result = None
addend = point
while k:
if k & 1:
# Add.
result = point_add(result, addend)
# Double.
addend = point_add(addend, addend)
k >>= 1
assert is_on_curve(result)
return result
# Keypair generation and ECDHE ################################################
def make_keypair():
"""Generates a random private-public key pair."""
private_key = curve.n
public_key = scalar_mult(private_key, curve.g)
return private_key, public_key
private_key, public_key = make_keypair()
print("private key:", hex(private_key))
print("public key: (0x{:x}, 0x{:x})".format(*public_key))
假设椭圆曲线方程为,发送方和接收方选取的私钥k=7,基点P为(0,1),假设发送方想要把一个数4发送给接收方,那么先将x=4带入曲线方程,得到明文M(4,4)。再根据k和P计算出公钥Q=7P=(42, 14),随机选一个数r=3,那么密文c= E(M)=(rP,M+rQ)=((19, 28), (6, 45))。
接收方知道了密文c和私钥k,只需要按照解密法则M=D(c)= M+rQ-krP就可以求出明文M(4,4)
#coding:gbk
p = 53
i = lambda x: pow(x, p-2, p)
def add(A, B):#加法运算
(u, v), (w, x) = A, B
assert u != w or v == x
if u == w: m = (3*u*w + 1) * i(v+x)
else: m = (x-v) * i(w-u)
y = m*m - u - w
z = m*(u-y) - v
return y % p, z % p
def opposite(A):#取A的相反数,也就是将A变成-A
return A[0],(-A[1])%p
def mul(t, A, B=0):#乘法运算
if not t:
return B
if t%2==0:
return mul(t//2, add(A,A), B)
elif B!=0:
return mul(t//2, add(A,A), add(B,A))
else:
return mul(t//2, add(A,A),A)
M=(4,4)
P=(0,1)
r=3
k=7
Q=mul(k,P)
c=(mul(r,P),add(M,mul(r,Q)))
print("公钥Q是",Q)
print("密文c是",c)
print("明文M是",add(c[1],opposite(mul(k,c[0]))))
(2)椭圆曲线数字签名
椭圆曲线数字签名算法,它利用椭圆曲线密码学(ECC)对数字签名算法(DSA)进行模拟,其安全性基于椭圆曲线离散对数问题。
但是当某些数值相同时会出现一些安全问题。 分析代码可以看出,存在随机数重复使用。具体来说,这段代码中签名的过程中使用了相同的随机数 k 来对不同的消息进行签名。这种情况下,可以通过分析两个相同 k 值对应的消息签名来恢复私钥 dA。
在 ECDSA 中,每次签名过程中都会使用一个随机数 k,以确保生成唯一的签名。然而,如果相同的随机数 k 被重复使用来对不同的消息进行签名,攻击者就有可能通过数学分析和推导计算出私钥 dA。
import sympy
from hashlib import sha1
from Cryptodome.Util.number import long_to_bytes , bytes_to_long
def calculate_private_key(r1, s1, s2, h1, h2, n):
# 计算k值
k = ((h1 - h2) * sympy.mod_inverse(s1 - s2, n)) % n
# 计算私钥dA
dA = (sympy.mod_inverse(r1, n) * (k * s1 - h1)) % n
return dA
if __name__ == "__main__":
# 定义椭圆曲线的参数
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
# 签名中的r1, s1, s2值
r1 = 4690192503304946823926998585663150874421527890534303129755098666293734606680
s1 = 111157363347893999914897601390136910031659525525419989250638426589503279490788
s2 = 74486305819584508240056247318325239805160339288252987178597122489325719901254
h1 = bytes_to_long(sha1(b'Hi.').digest())
h2 = bytes_to_long(sha1(b'hello.').digest())
private_key = calculate_private_key(r1, s1, s2, h1, h2, n)
print(f'flag{{{private_key}}}')
4.DSA
5.ElGamal
(五)国密
(六)用提取、删除、替换字符
grep -o '[A-Z]' 1.txt | tr -d '\n' >>2.txt sed -i -e 's/ZERO/0/g' -e 's/ONE/1/g' 2.txt
sed 's/v[0-9]\+\s*=\s*//g' 1.txt | sed 's/u//g' | tr -d '\n ' | tr ';' ',' > output.txt删除v1-v43、u、换行、替换;为,

(七)01或者AB这种相反面
带有相反面的,比如黑白这种,想到转换成二进制0101或者摩斯密码.-.-
或者培根密码
(八)Linux系统的 shadow 文件格式
特征:就是Linux的shadow文件格式。。。
工具:Kali Linux 中的 John
e.g.
root:$6$HRMJoyGA$26FIgg6CU0bGUOfqFB0Qo9AE2LRZxG8N3H.3BK8t49wGlYbkFbxVFtGOZqVIq3q Q6k0oetDbn2aVzdhuVQ6US.:17770:0:99999:7:::
Linux的 /etc/shadow 文件存储了该系统下所有用户口令相关信息,只有 root 权限可以查看,用户口令是以 Hash + Salt 的形式保护的。 每个字段都用 “$” 或“:”符号分割; 第一个字段是用户名,如root ; 第二个字段是哈希算法,比如 6 代表SHA-512,1 代表 MD5; 第三个字段是盐,比如上面的 HRMJoyGA 第四个字段是口令+盐加密后的哈希值 后面分别是密码最后一次修改日期、密码的两次修改间隔时间(和第三个字段相比)、密码的有效期(和第三个字段相比)、密码修改到期前的警告天数(和第五个字段相比)、密码过期后的宽限天数(和第五个字段相比)、账号失效时间,这里不太重要要;
直接跑 John 试试
john shadow
如果解开了,加 --show 查看解密口令
john --show shadow
(九)MD5
特征:一般为16位或32位 ,由数字和小写字母组成
0906b080b03ea64d0534d36b2bd9edb8

























 2437
2437

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








