Z变换和离散时间傅里叶变换（DTFT）知识点总结

一.序列的Z变换

1.定义

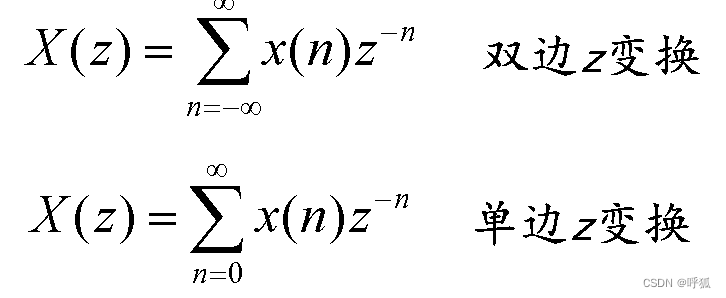
根据起始值的不同可分为单边、双边Z变换。其中因果序列的两种变换结果相同，一般用双边Z变换计算。

2.Z变换收敛域

在有理分式形式中，总是用极点界定其边界。

以下为四种典型收敛域：

1) 有限长序列z 变换的收敛域   0<|z|<无穷

2）因果序列，收敛域在z平面上半径为|a|的圆外区域二。

3）反因果序列，收敛域在z平面上半径为|b|的圆内区域

4）双边序列当|a|<|b|时ZT存在，敛域为|a|<|z|<|b|的环状区域

二.序列的傅里叶变换

1.定义

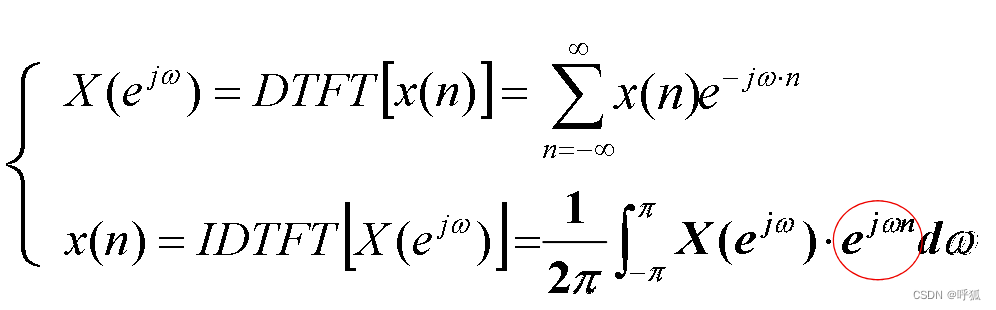
变换后的X为x（n）的频谱。特点：连续函数，以2π为周期，是的复函数。

2.存在条件

1）x（n）绝对可和---充分条件

2）x（n）平方可和

3）引入冲激函数

序列的z变换与序列的傅里叶变换的关系：

序列在单位圆上的z变换=序列的傅里叶变换

求序列傅里叶变换的方法：直接用定义；先求z变换。

常用序列的DTFT：

3.DTFT主要性质

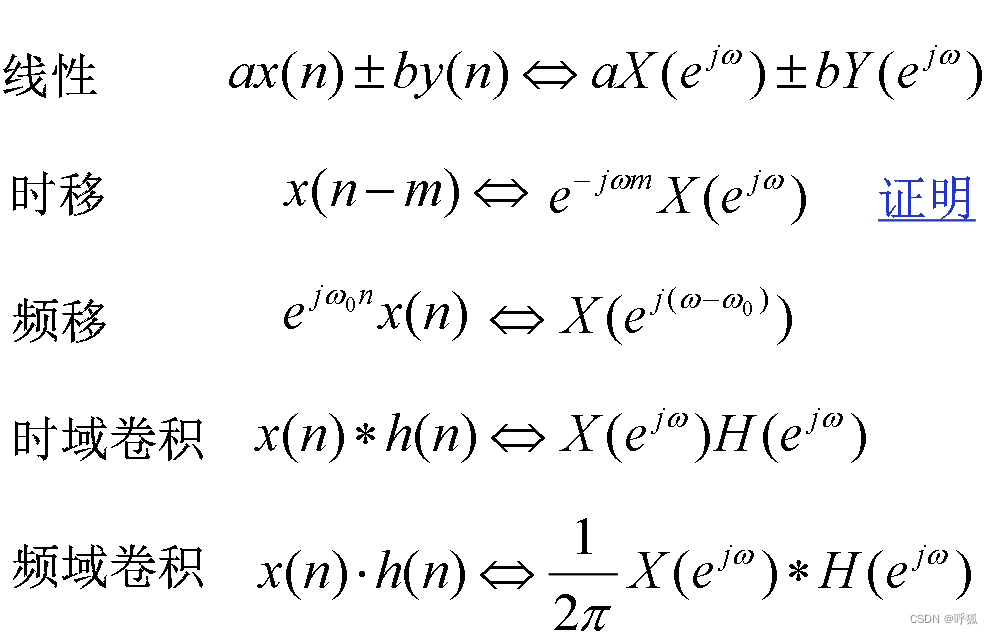
4.DTFT的一些对称性质

1）

共轭对称序列：实部偶对称，虚部奇对称

共轭反对称序列：实部奇对称，虚部偶对称

任意序列x(n)总能表示成一个共轭对称序列与一个共轭反对称序列之和

序列的傅里叶变换可以分解为共轭对称分量与共轭反对称分量之和

2）序列傅立叶变换的对称性

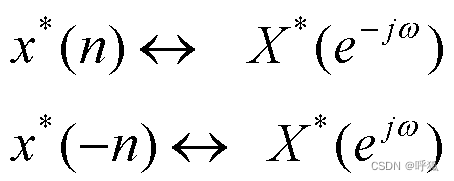
x(n)为实数偶对称，X（e为实数偶对称

实奇对虚奇

三.序列的z变换与连续信号的拉普拉斯变换、傅里叶变换的关系

连续信号的傅里叶是虚轴上的拉氏变换

序列的傅里叶是单位圆上的Z变换

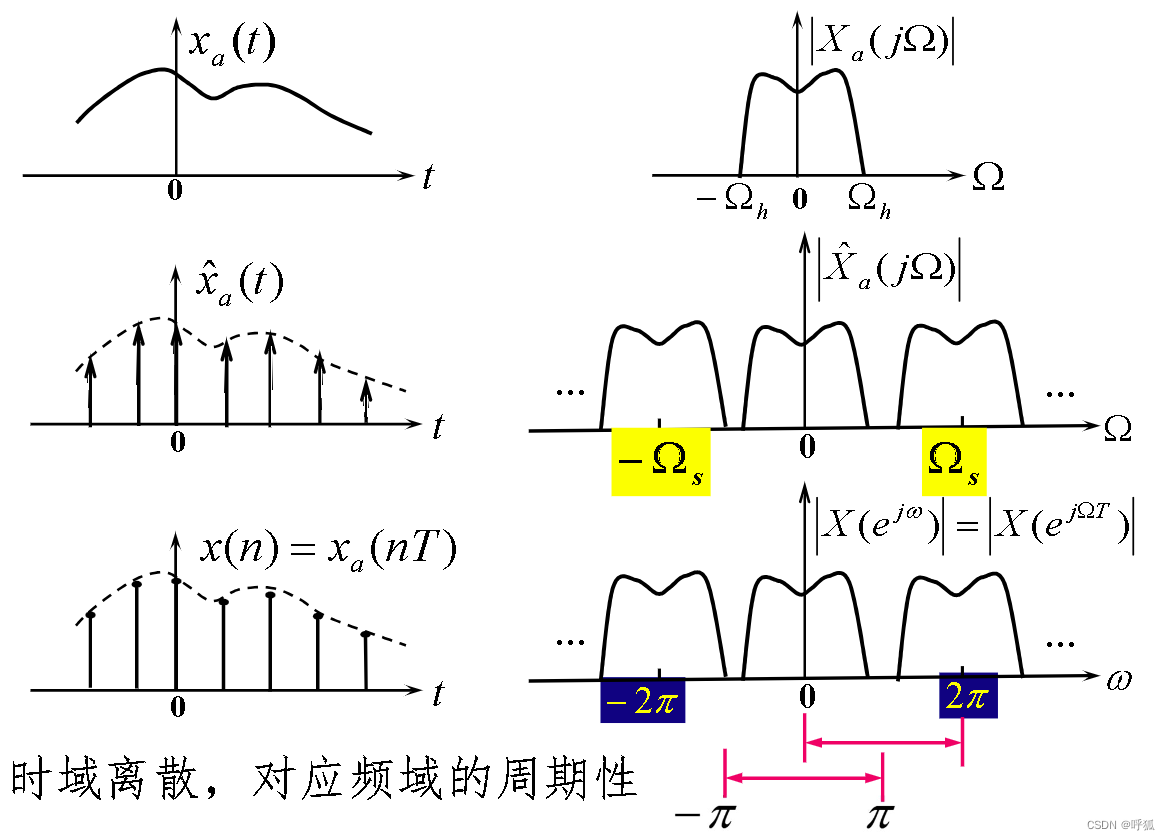
从理想采样信号的拉普拉斯变换到采样序列的z变换，就是由复变量s平面到复变量z平面的映射,其映射关系为：

多对一的映射

序列的傅里叶变换等于其理想抽样信号的傅里叶变换

抽样序列频谱是其理想抽样信号的傅里叶变换，即原连续信号的频谱周期延拓

四.离散LSI系统的频域表征

1、系统的几种描述方法

单位序列响应系统函数频率响应：

系统函数：

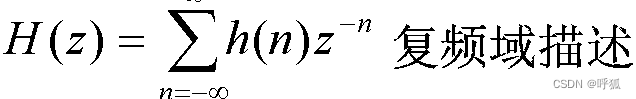
频率响应：

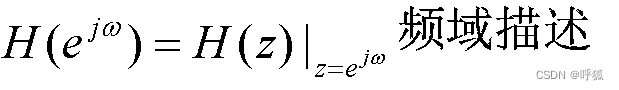
常系数线性差分方程零、极点图、方框图

2.离散时间系统的稳定性和因果性

1）系统的因果性

a.从时域判断

h（n）=0  n<0;

b.从频域判断

2）系统的稳定性

满足输入有界，输出有界

a.时域分析

b.变换域分析

3）因果稳定系统

极点都在单位圆内